基于改进TDOA的近场声源鲁棒定位方法研究

曹 洁 吴尧帅 李 伟2, 王进花

1(兰州理工大学计算机与通信学院 甘肃 兰州 730050) 2(甘肃省制造业信息化工程研究中心 甘肃 兰州 730050) 3(兰州理工大学电气工程与信息工程学院 甘肃 兰州 730050)

0 引 言

声源定位是音频信号处理领域中的一个重要研究课题，在智能机器人[1]，盲点探测(BSD)[2]，水下侦察[3]等领域都有着广泛的应用。经过几十年的发展，声源定位算法可主要分为三种：第一种是基于高分辨率谱估计定位技术[4]，一般多用于多声源定位，但计算复杂度太高；第二种是基于可控波束形成的定位技术[5]，通过扫描整个空间域的点，探索能够使波束功率最大的点，计算量较大；第三种是基于时间到达差(TDOA)的算法，该算法主要分为两个步骤：时延估计与定位估计，基本原理是利用多路同步语音信号的相关性，得到声源到麦克风间的TDOA，再通过几何关系得到声源位置坐标，该方法具有结构简单，计算量小的优点。

目前，最常用的时延估计算法是相位变换加权广义互相关(GCC-PHAT)[6]。但在真实声音环境中，较强的背景噪声，致使麦克风阵列接收的音频信号信噪比变低。传统的GCC-PHAT算法对宽带噪声敏感，性能急剧恶化，使定位误差增大。为此，张大威等[7]提出了基于传递函数比的统计模型方法(ATFR-SM)，通过构造噪声统计模型，提高音频信号信噪比，但在非高斯噪声背景下效果不明显；Dong等[8]参考有限冲激响应(FIR)滤波器，提出了参数识别(Parameter Identification)的时延估计算法，在一定程度上提高了时延估计的性能，但是计算复杂度较高，不利于实时实现。针对近场声源定位，通常采用最小二乘(LS)算法估计定位信息，但需要搜索全空域，会产生大量冗余[9]。为此，Torrieri[10]将LS中的方程按泰勒级数展开，降低了运算量，但极易产生误差；Qu等[11]提出了凸约束加权最小二乘算法，但需要已知音频噪声的先验信息，在实际应用中具有局限性。

基于上述分析，针对低信噪比下传统时延性能差以及定位估计算法计算量大的问题，本文在传统的基于TDOA的近场声源定位算法的基础上进行改进。首先，在时延估计前，利用FIR维纳滤波器，对每路语音信号进行预处理，提高语音信号的信噪比，提高时延估计的准确性。其次，在传统LS算法的基础上提出空域收缩迭代最小二乘算法，降低算法的计算复杂度。最后，通过实验仿真，对本文提出的定位方法进行验证。

1 TDOA近场声源定位

1.1 声场模型

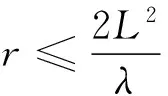
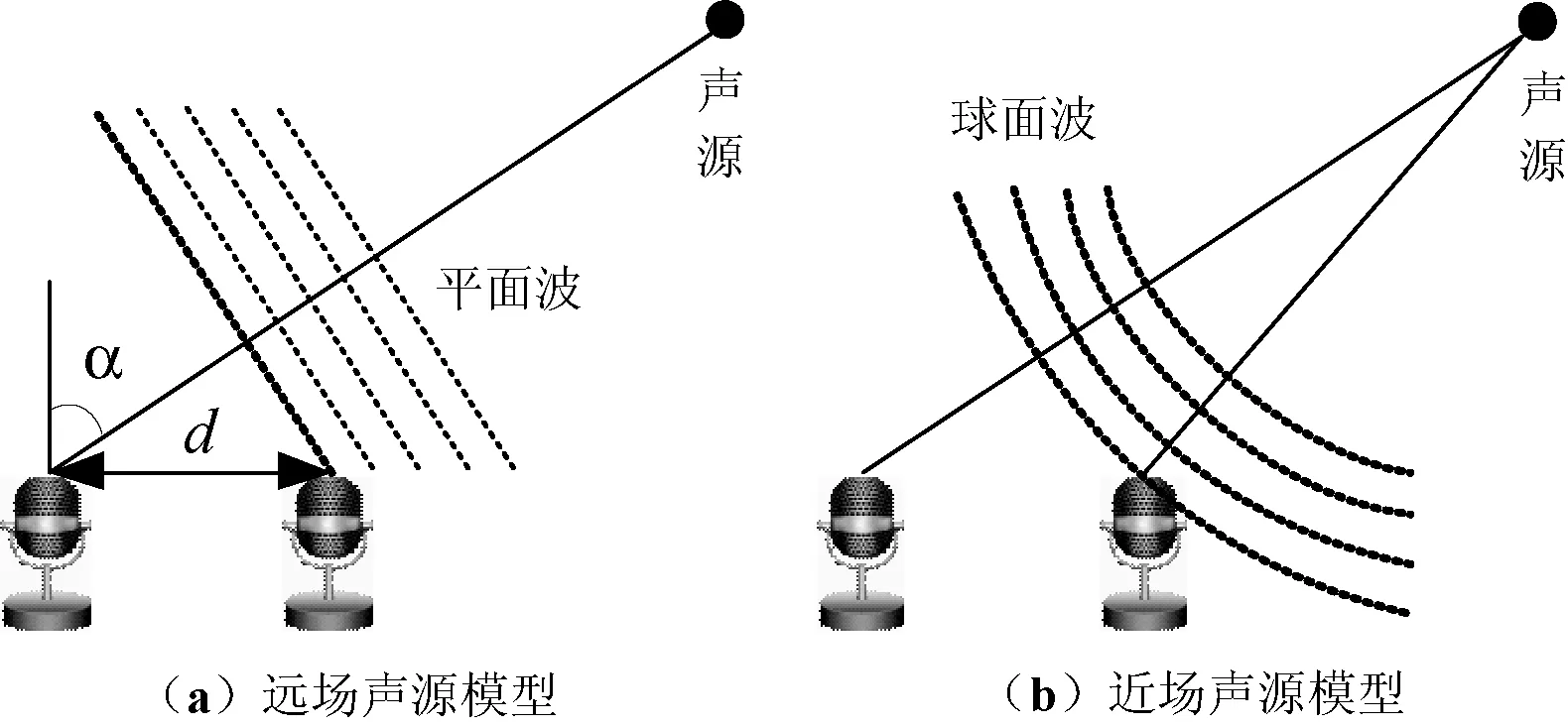
图1 音频信号声场模型

1.2 时延估计

广义互相关(GCC)方法[12]是最经典的时延估计算法，其核心思想是通过计算一对麦克风所接收信号的互相关函数，该互相关函数的峰值就对应于声源信号到达该对麦克风的时延差。

首先，构建音频信号模型。设其中第a个麦克风与第b个麦克风接收信号为：

xa(n)=sa(n)+ωa(n)

(1)

xb(n)=sb(n+τ)+ωb(n)

(2)

式中：xa(n)和xb(n)是两个麦克风接收的信号，ωa(n)和ωb(n)是互不相关的背景噪声，τ是声源到两个麦克风间的时延。

(3)

式中：τ为时延，k为频率。该对麦克风的时延就是函数Ψab(τ)的峰值对应的τ值。

然而，实际声学环境中的噪声会直接影响相关函数，弱化相关峰，甚至出现多个伪峰，这是造成τ值检测困难的主要原因。因此，计算两个麦克风之间的时延常通过加权的方法得到，时延效果最好的加权函数为互功率谱相位加权(PHAT)函数[13]：

(4)

互相关函数则转化为：

(5)

1.3 基于时延估计的近场声源定位方法

依据麦克风阵列拓扑结构，构造笛卡尔坐标系，给每一个麦克风赋予一个三维坐标值，再结合时延估计得到τ值，获得声源的三维坐标。常用的方法有线性插值法[14]和球形插值法[15]，线性插值法对麦克风阵列拓扑结构要求严格，而且近场声源定位误差较大；球形插值法对麦克风阵列拓扑结构没有严格的要求，通过首先设定一个参考麦克风，求其他麦克风相对于参考麦克风的时延，之后根据时延和各个麦克风的位置坐标，构建误差方程组，利用LS算法求得位置坐标的最优解。球形插值法结构清晰简单，易于理解，适合近场声源定位。

在一个由m个麦克风组成的麦克风阵列中，假设第i个麦克风的位置坐标表示为(xi,yi,zi)(i=1,2,…,m)，声源位置坐标表示为(xs,ys,zs)，第i个麦克风到第1个麦克风的时延为τi。则：

di1=di-d1=

i=2,3,…,m

(6)

式中：di和d1分别表示声源到第i个麦克风和到第1个麦克风的距离，di1表示声源到第i个麦克风和到第1个麦克风的距离差，c表示声速。

在理想情况下，声源位置就是笛卡尔坐标系中双曲面的交点，可以通过联立曲线方程求解。然而，由于环境中声速的不确定性与时延估计误差的存在，这个交集往往是空集。定位估计的重点就是如何采用搜索算法估计真正的声源位置，减小定位误差。目前最常用的定位估计算法是最小二乘法(LS)。原理如下：

由式(6)，得到：

di1=d1+di

(7)

式(7)两边平方：

(xi-x1)(xs-x1)+(yi-y1)(ys-y1)+

(zi-z1)(zs-z1) +di1d1=

(8)

将式(8)表示为矩阵形式，得到：

Aθ=b

(9)

式中：

(10)

θ=[xs-x1ys-y1zs-z1d1]T

(11)

(12)

通过搜索全空域中所有的点，得到：

(13)

根据得到的θLS值，得到声源坐标。

2 本文方法

首先利用FIR维纳滤波器对音频信号预处理，依靠维纳滤波器较高的自然统计特性，提高音频信号信噪比，利用时延估计方法得到τ;再根据要求的精度，利用空域迭代最小二乘算法得到目标声源位置信息。本文方法如图2所示。

图2 本文声源定位方法流程

2.1 音频信号预处理

为提升时延估计性能，引入FIR维纳滤波器对音频信号预处理以提高音频信号的信噪比。FIR维纳滤波器只适用于平稳信号，而音频信号多为非平稳宽带信号，因此将音频信号分帧，逐帧进行滤波处理，再将每一帧语音信号重新组合。维纳滤波器的功能是使输出y(n)在均方意义上最优的逼近希望信号d(n)，因此，逼近的结果是使y(n)在最大程度上去除噪声，可以最大程度地保留原语音信号的频域分布。本文截取100个采样点为一个语音帧，设麦克风接收的信号为x(n)，即有：

(14)

式中：rx(k-m)=E{x(n-m)x(n-k)}是x(n)的自相关函数，rdx(k)=E{d(n)x(n-k)}是d(n)和x(n)的互相关函数,h(m)为维纳滤波器系数。

令h是h(0),h(1),…,h(99)组成的100×1的滤波器向量组，rdx是由rdx(0),rdx(1),…,rdx(99)组成的100×1的互相关向量，R为M×M的自相关矩阵，显然，R是Toeplitz矩阵。

则式(14)可写成矩阵形式：

Rh=rdx

(15)

将式(15)两边分别乘上R的逆矩阵：

h=R-1rdx

(16)

则最小均方误差可表示为:

(17)

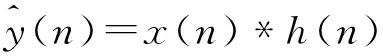
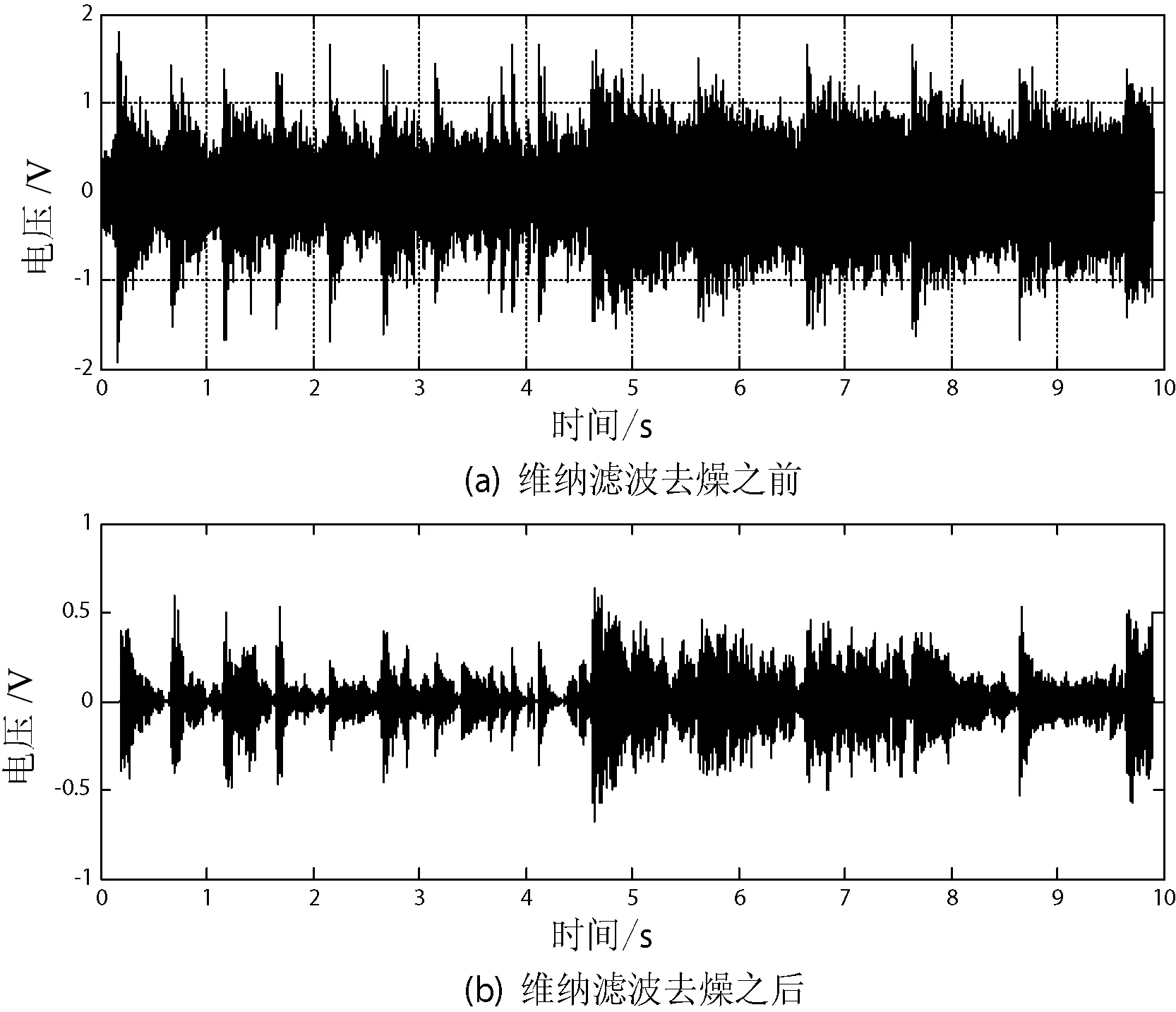
图3 维纳滤波去噪前后

2.2 本文时延估计方法

本文所采用的时延估计方法主要分为四个步骤：加窗分帧、基音检测(VAD)、去混响和GCC-PHAT。将信号利用哈明窗截取帧长为512数据点，取每帧音频信号的后半帧作为下一帧的前半帧，构建重叠帧。对每帧数据作基音检测，找出语音数据帧，将非语音帧去除，减少计算量。利用复倒谱技术处理语音信号的混响，倒谱技术通过时域卷积，将卷积运算转换为加法运算。音频信号一般位于倒谱域的原点附近，而混响信号则离原点较远，因此，在倒谱域内可通过低通滤波器削减混响。最后，利用GCC-PHAT算法得到τ。

为验证本文时延估计方法性能，用一对麦克风接收的音频信号作为实验数据，其中，采样率为16KHz，理论时延采样点为140点。将这组数据采用本文时延方法与传统的GCC-PHAT[13]算法对比实验，实验结果如图4所示。利用传统的GCC-PHAT时延估计得到的实验采样点为149点，而本文时延方法得到的实验采样点为145点。可以看出，本文时延互相关序列旁瓣比明显小于传统的GCC-PHAT算法，峰值更加突出，而且本文时延估计误差也小于传统的GCC-PHAT算法。

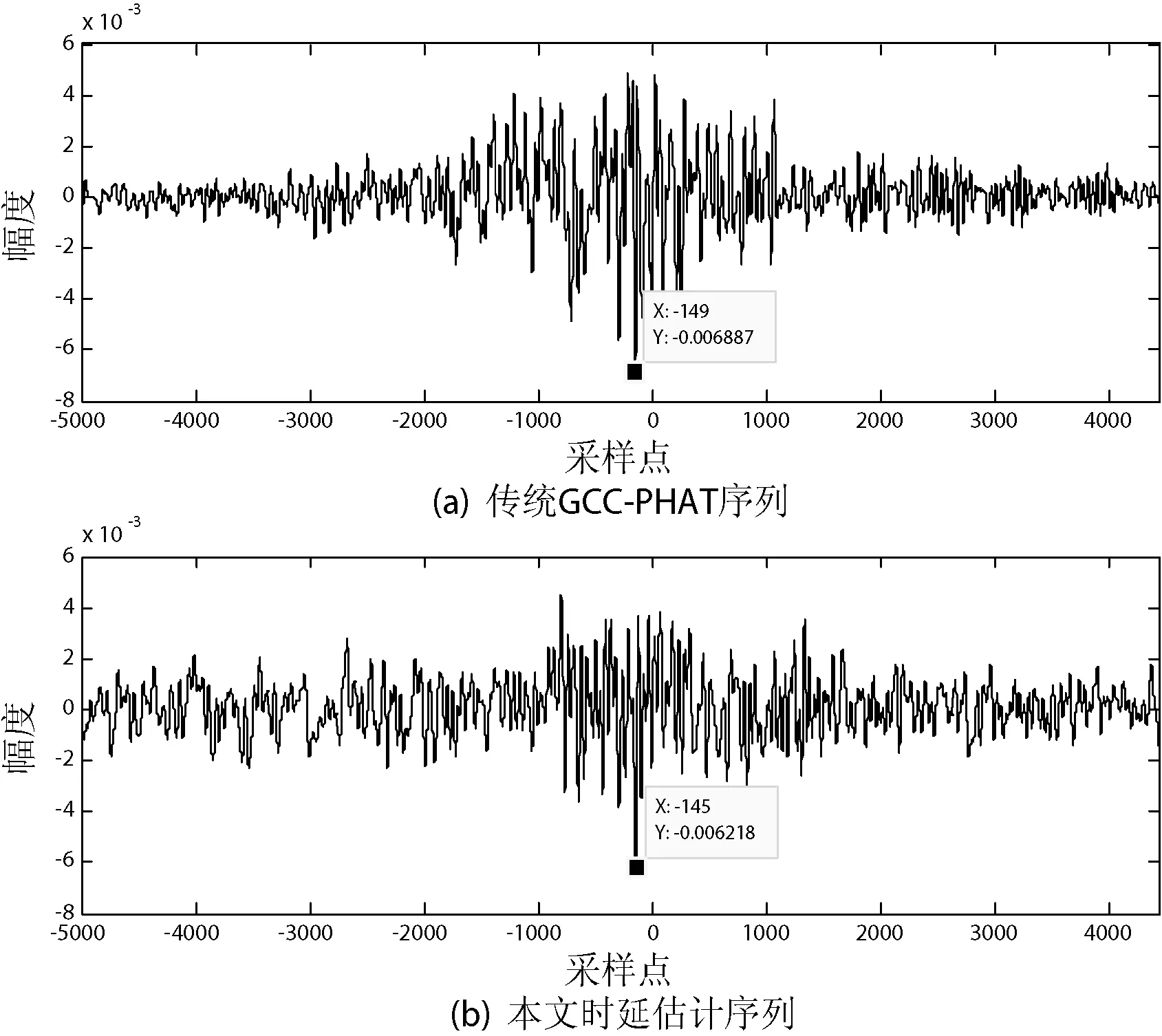
图4 时延估计对比实验结果

2.3 空域收缩迭代最小二乘法

本文提出空域收缩迭代最小二乘算法，降低LS算法的计算复杂度。若目标声源在一个V的三维空域内，收缩度为d，整个算法过程可归纳为：

(1) 初始化迭代，即i=0，V0=V，设置初始空间分辨率r0；

(2) 空域搜索，即利用式(13)，以ri为空间分辨率在空域Vi内搜索最大似然点θi；

(3) 检测结果，即如果θi符合预定精度范围，则θLS=θi，否则进行第(4)步；

(5) 空域收缩，即以θi为空域中心，0.5*ri-1为边长重新设定搜索空域Vi，转向第(2)步。

2.4 计算复杂度分析

设在预设精度范围内，通过空域收缩迭代最小二乘算法得到声源位置坐标，此刻的空间采样率为ri，则算法的计算量为：

Nm1=[(2i+1)(d+1)]3

(18)

而在预设精度范围内，通过传统LS算法得到声源位置坐标，则算法的计算量为：

N2=(di+1+1)3

(19)

比较N1与N2，当i>0时，N1>N2，即空域收缩迭代最小二乘算法的计算量小于传统LS算法。

传统LS算法是在高空间分辨率的条件下，搜索全空域，而本文提出的方法首先在低空间分辨率下，搜索全空域，得到一个最大似然值，缩小搜索空域，提高空间分辨率，如此反复迭代直到达到预设精度范围位置。因此，本文提出的算法的计算复杂度可以近似由式(18)表示，传统LS算法的计算复杂度可以近似由式(19)表示。综上所述，本文所提出的空域收缩迭代最小二乘算法相比于传统LS算法，能够显著地降低算法的计算复杂度。

3 实验分析

3.1 实验环境

本文利用如图5所示的八元圆形麦克风阵列进行仿真实验，其中麦克风为快鱼P21LZ，阵列半径为0.1 m。将其放置在一个尺寸为8 m×5 m×3 m的房间内。计算机软件处理平台为Lenovo TS50X，内存4 GB，CPU为i3-4160。

图5 八元圆形麦克风阵列

为验证本文提出方法的有效性，本文针对不同噪声环境下的声源进行了声源定位的仿真实验，与文献[13]中的基于TDOA的声源定位方法，文献[5]提出的基于可控功率响应相位加权(SRP-PHAT)的定位方法作对比。通过将录制的音频信号与不同的背景噪声相叠加模拟出不同的低信噪比环境。由于标准噪音库noiseX-92中的白噪声，粉红噪声，babble噪声最接近真实场景下的噪声，因此本文依次选取这三种噪声作为背景噪声。信噪比分别设定为5、10、15、20 dB。实验中语音信号采样频率为16 KHz，帧长为512，帧叠为50%，统计帧数为64。为验证本文提出方法在不同空间位置的实验效果，以麦克风阵列中心为坐标原点构建笛卡尔坐标系，本文分别录制目标声源位于位置1(1 m,0 m,1.1 m)，位置2(1 m,1 m,1.1 m)和位置3(0 m,1 m,1.1 m)的语音信号，每段语音长度为5s，经过100次蒙特卡洛仿真实验得到实验结果。收缩度设为10，实验结果精度设为0.001 m。

3.2 性能指标

本文采用均方根误差(RMSE)度量定位效果，定义为：

(20)

式中：J为仿真次数，(xi,yi,zi)和(x0,y0,z0)分别表示第i次实验声源位置的实验所得坐标值和真实坐标值。RMSE用来衡量定位方法所得值在真实值附近的分布，这个值越小，表明定位方法所得值分布在真实值附近，即表示此方法效果越好。

3.3 实验结果分析

为验证本文提出方法在不同噪声背景下的实验效果，本文分别在背景噪声为白噪声、粉红噪声与babble噪声时做对比实验。

从表1中可以观察到，背景噪声是白噪声的环境下，随着SNR的提高，三种方法的定位误差均有不同程度的减小。定位准确度方面，总体上文献[5]方法与本文方法精确度相差不大，但都比文献[13]方法精确度提高23%左右。定位实时性方面，从图6中可以观察到，不同信噪比下，本文方法比文献[13]方法的耗时都减少了11%左右，本文方法比文献[5]方法的耗时都减少了30%左右。

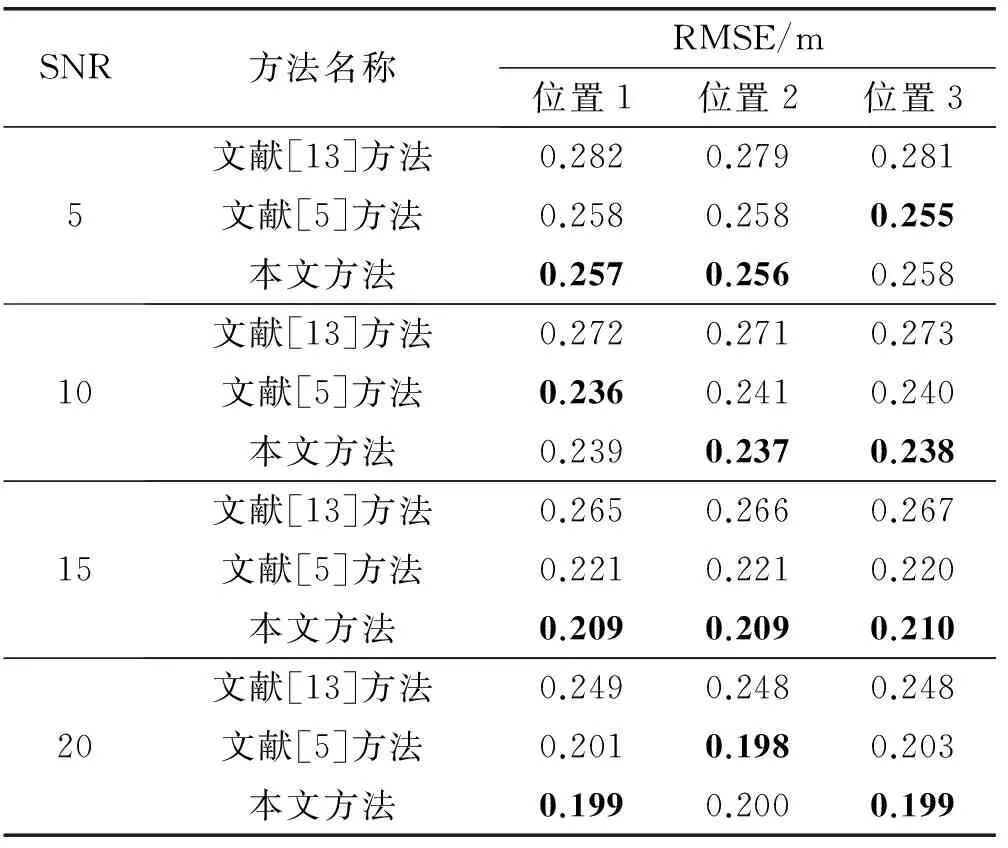
表1 白噪声背景下声源定位

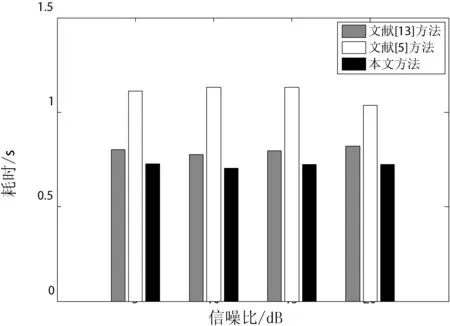
图6 白噪声背景下不同定位方法的耗时

从表2中可以观察到，背景噪声是粉红噪声的环境下，随着SNR的提高，三种方法的定位误差均有不同程度的减小。定位准确度方面，总体上文献[5]方法与本文方法精确度相差不大，但都比文献[13]方法精确度提高11%左右。定位实时性方面，从图7中可以观察到，不同信噪比下，本文方法比文献[13]方法的耗时都减少了12%左右，本文方法比文献[5]方法的耗时都减少了29%左右。

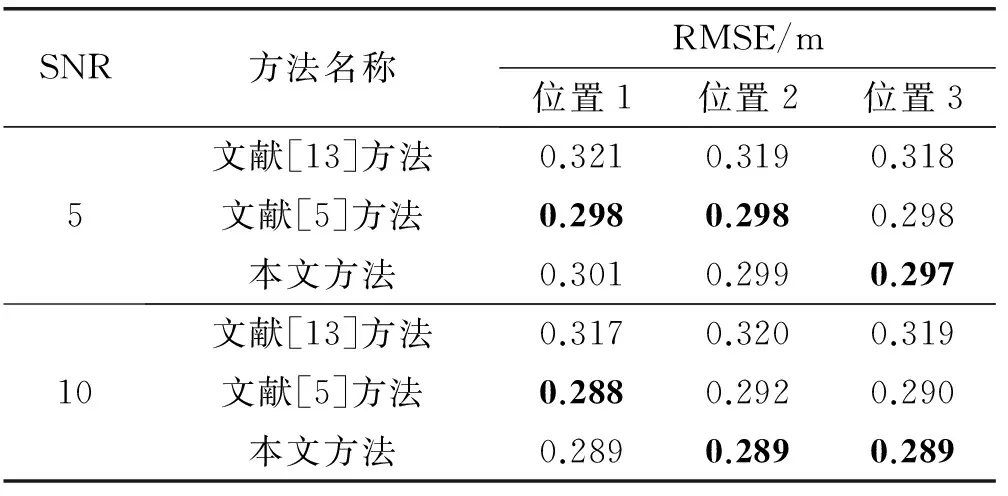
表2 粉红噪声背景下声源定位

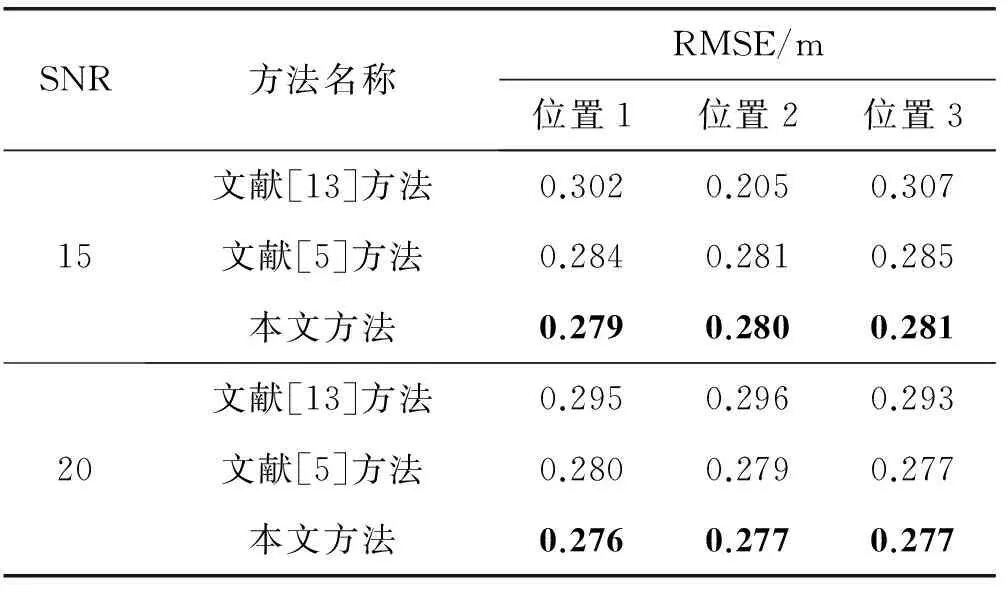
续表2 粉红噪声背景下声源定位

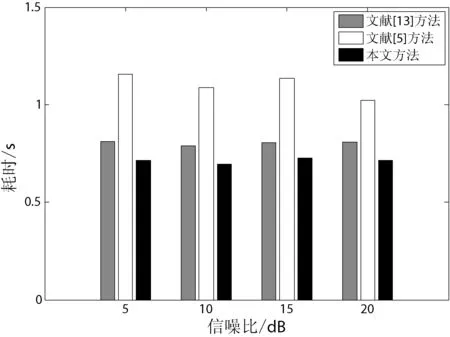
图7 粉红噪声背景下不同定位方法的耗时

从表3中可以观察到，背景噪声是babble噪声的环境下，随着SNR的提高，三种方法的定位误差均有不同程度的减小。定位准确度方面，总体上文献[5]方法与本文方法精确度相差不大，但都比文献[13]方法精确度提高12%左右。定位实时性方面，从图8中可以观察到，不同信噪比下，本文方法比文献[13]方法的耗时都减少了11%左右，本文方法比文献[5]方法的耗时都减少了26%左右。

表3 babble噪声背景下声源定位

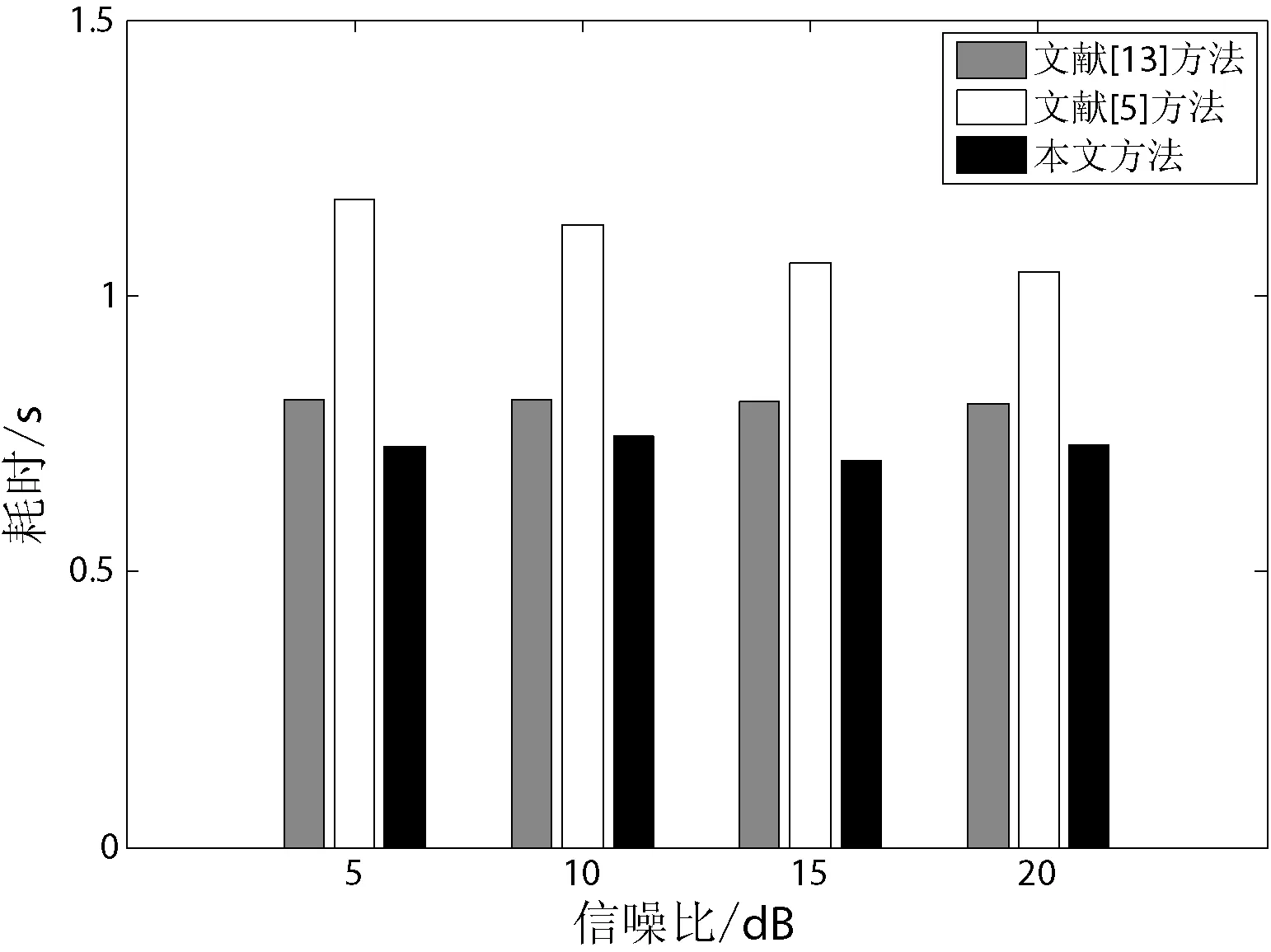
图8 babble噪声背景下不同定位方法的耗时

4 结 语

低信噪比环境下近场声源定位普遍存在两个问题：音频信号中的环境噪声将提高互相关序列的旁瓣比，致使时延性能降低，鲁棒性差；近场声源定位估计算法计算量大，降低了定位方法的实时性。为此，本文提出了一种改进的基于TDOA鲁棒声源定位方法。理论分析和实验结果均证明了本文提出的方法的优越性。下一步的工作将研究如何将本文定位方法与贝叶斯理论相结合，融入声源位置的先验信息提高低信噪比环境下的声源定位精度。

[1] Sreejith T M,Joshin P K,Harshavardhan S,et al.TDE sign based homing algorithm for sound source tracking using a Y-shaped microphone array[C]//2015 23rd European Signal Processing Conference.IEEE,2015:1202-1206.

[2] Jang Y,Kim J,Kim J.The development of the vehicle sound source localization system[C]//Asia-Pacific Signal and Information Processing Association Summit and Conference.2015:1241-1244.

[3] Zhang W,Zeng X,Gong C,et al.Precision analysis of underwater acoustic source localization using five-element plane cross array[C]//Ocean Acoustics (COA),2016 IEEE/OES China.IEEE,2016.

[4] Takeda R,Komatani K.Performance comparison of MUSIC-based sound localization methods on small humanoid under low SNR conditions[C]//IEEE-RAS,International Conference on Humanoid Robots.IEEE,2015:859-865.

[5] 张一闻,刘建平,张世全.利用多点互相关值均值的实时声源定位算法[J].西安电子科技大学学报(自然科学版),2015,42(1):168-173.

[6] 崔玮玮,曹志刚,魏建强.声源定位中的时延估计技术[J].数据采集与处理,2007,22(1):90-99.

[7] 张大威,鲍长春,夏丙寅.复杂环境下基于时延估计的声源定位技术研究[J].通信学报,2014,35(1):183-190.

[8] Dong Z,Yu M.Research on TDOA based microphone array acoustic localization[C]//IEEE International Conference on Electronic Measurement & Instruments.IEEE,2015:1077-1081.

[9] Li X,Deng Z D,Rauchenstein L T,et al.Contributed Review:Source localization algorithms and applications using time of arrival and time difference of arrival measurements[J].Review of Scientific Instruments,2016,87(4):041502.

[10] Torrieri D J.Statistical Theory of Passive Location Systems[J].IEEE Transactions on Aerospace & Electronic Systems,1984,20(2):183-198.

[11] Qu X,Xie L.An efficient convex constrained weighted least squares source localization algorithm based on TDOA measurements[J].Signal Processing,2016,119(C):142-152.

[12] Knapp C,Carter G.The generalized correlation method for estimation of time delay[J].IEEE Transactions on Acoustics Speech & Signal Processing,1976,24(4):320-327.

[13] 张传义,米常伟.基于TDE技术的声源定位算法[J].东北大学学报(自然科学版),2014,35(3):333-336.

[14] 于振华,付晓,王静,等.基于声学无线传感器网络的目标跟踪系统研究[J].电子科技大学学报,2011,40(4):568-572.

[15] Don Y,Wang H,Ma S.An algorithm of sound source localization using range differences of arrival and energy ratios of arrival[C]//Industrial Electronics and Applications (ICIEA),2016 IEEE 11th Conference on.IEEE,2016:1547-1550.