基于LSTM和Kalman滤波的公交车到站时间预测
2018-05-03范光鹏孙仁诚邵峰晶
范光鹏 孙仁诚 邵峰晶
(青岛大学计算机科学技术学院 山东 青岛 266071)
0 引 言
随着国民经济的发展,私家车数量越来越多,给城市交通带来巨大压力,交通问题已成为城市发展面临的巨大问题,因此建设智能交通系统是城市交通建设的主要任务。在智能交通系统中,发展公共交通系统是缓解城市交通压力的主要手段,因此公共交通系统在智能交通系统建设中仍占有主体地位。公共交通系统应该能实时反映公交车的运行状况,因此公交车到站时间预测是公共交通系统的主要功能之一。为此各国学者做了大量研究,其预测模型主要有以下两类:
第一类模型是基于历史交通状况、路段特征和到达各站点的历史时间规律预测公交车到达各站点的时间。主要有以下方法:
Jeong等[1]利用车辆自动定位数据,将公交车时刻表,道路拥挤和车辆停靠时间等作为变量,分别建立了时间序列模型、回归模型和人工神经网络模型预测公交车到站时间,结果显示人工神经网络要优于其他模型。
陈鹏[2]建立了基于人工神经网络的公交车到站时间预测模型,并结合调度员的调度经验、行车计划等对算法进行了优化。最终建立了智能实时调度模型。
于滨等[3]利用支持向量机预测公交车运行时间,采用了时间段、天气和路段以及当前路段的运行时间和下一路段的最新运行时间5个输入变量。最后,应用大连市开发区4路公交线对该模型进行了校验。
然而公交车行驶时间是动态变化的,当预测数据相对历史数据发生较大变化时,会对预测结果造成很大的影响。同时上述算法模型并没有充分利用时间序列的长短时变化特性,仅仅是基于相关变量对公交车到站时间的短时映射。
第二类预测模型先利用静态模型预测公交车到达各站点的时间,再利用动态调整模型根据观测数据动态调整预测值。主要有以下方法:
Chen等[4]利用车辆自动定位系统数据和自动乘客计数系统数据,建立了基于Kalman滤波的公交车到站时间动态预测模型。该模型以巴士行程时间表作为基础运行时间,根据公交车到达当前站点的观测值利用Kalman滤波调整到达下一站的基础时间,从而达到公交车到站预测时间动态调整的目的。
于滨等[5]建立了基于SVM和Kalman滤波的公交车到站时间预测模型,将时段、天气和路段作为SVM模型的输入特征值,预测公交车在每一路段行驶的时间并将其作为静态预测值。
Chien等[6]利用人工神经网络作为静态预测模型,将Kalman滤波模型作为动态调整模型对新泽西州运输公司第39号线路公交车行驶时间进行了预测。
计晓昕等[7]建立了组合非参数回归和Kalman滤波组合模型,以北京公交300路为例,对公交车到站时间进行了预测。
Kalman滤波模型根据历史数据和实时数据,对静态预测结果进行调整具有较高的预测精度,但是如果静态预测模型的预测值与真实值偏差较大,动态调整后的预测值的精确度会受到影响。目前对于静态模型使用较为广泛的是SVM模型,其并不能反映时间序列的长短时特性。基于上述静态预测模型的不足,本文提出基于LSTM和Kalman滤波的公交车到站时间预测模型。
1 公交车到站时间预测分析
公交车从始发站出发并再次到达始发站的过程称为车次。本文的目的是在一个车次中,预测公交车从始发站到达各站点所经历的时间。对于某一辆公交车,其行驶的路线虽然是固定的,但是在一天中不同的时段和不同的车次中公交车到达同一站点行驶的时间是不同的,所以公交车数据是一种动态变化的时间序列数据。从长期来看,各时间序列有着一定的变化趋势,从短期来看,不同的时间序列有着各自的变化趋势。
本文中的预测方法分为静态预测和动态调整两部分,首先利用静态预测模型预测公交车从始发站到达各站点所经历的时间,然后根据公交车到达各站点的观测时间利用动态调整模型对静态预测时间进行动态调整。
(1)

动态调整:公交车真实到站时间与静态预测时间是有偏差的,需要动态模型对静态模型预测值进行调整:
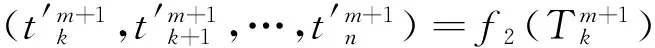
(2)
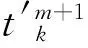
2 预测模型及算法步骤
本文利用长短时记忆递归神经网络LSTM[8-9]作为静态预测模型预测本车次中公交车到达各站点的行驶时间,以此作为基础时间序列。利用Kalman滤波[10]作为动态调整模型对基础时间进行动态调整。
如图1所示,一个车次中公交车经过n个站点,一天中公交车会有多个车次,每个车次的所有站点的三元组数据x组成了三元组数据序列。

图1 公交车数据
按时间展开的LSTM静态预测模型示意图如图2所示。从纵向看,每一个节点代表了神经网络的一层,分别是输入层、隐含层和输出层,从横向看,每一个节点代表了其在不同时刻的计算过程。在第m车次中,首先第一个站点的元数据输入LSTM神经网络,经隐含层输出;其次隐含层的输出和第2个站点的元数据作为下一个时刻LSTM神经网络计算的输入,以此类推,直到第n个站点的元数据计算完毕经隐含层输出到输出层;输出层分别输出下一个车次公交车从始发站出发以此到达各站点所经历的时间,这些时间组成的序列就是基础时间序列。
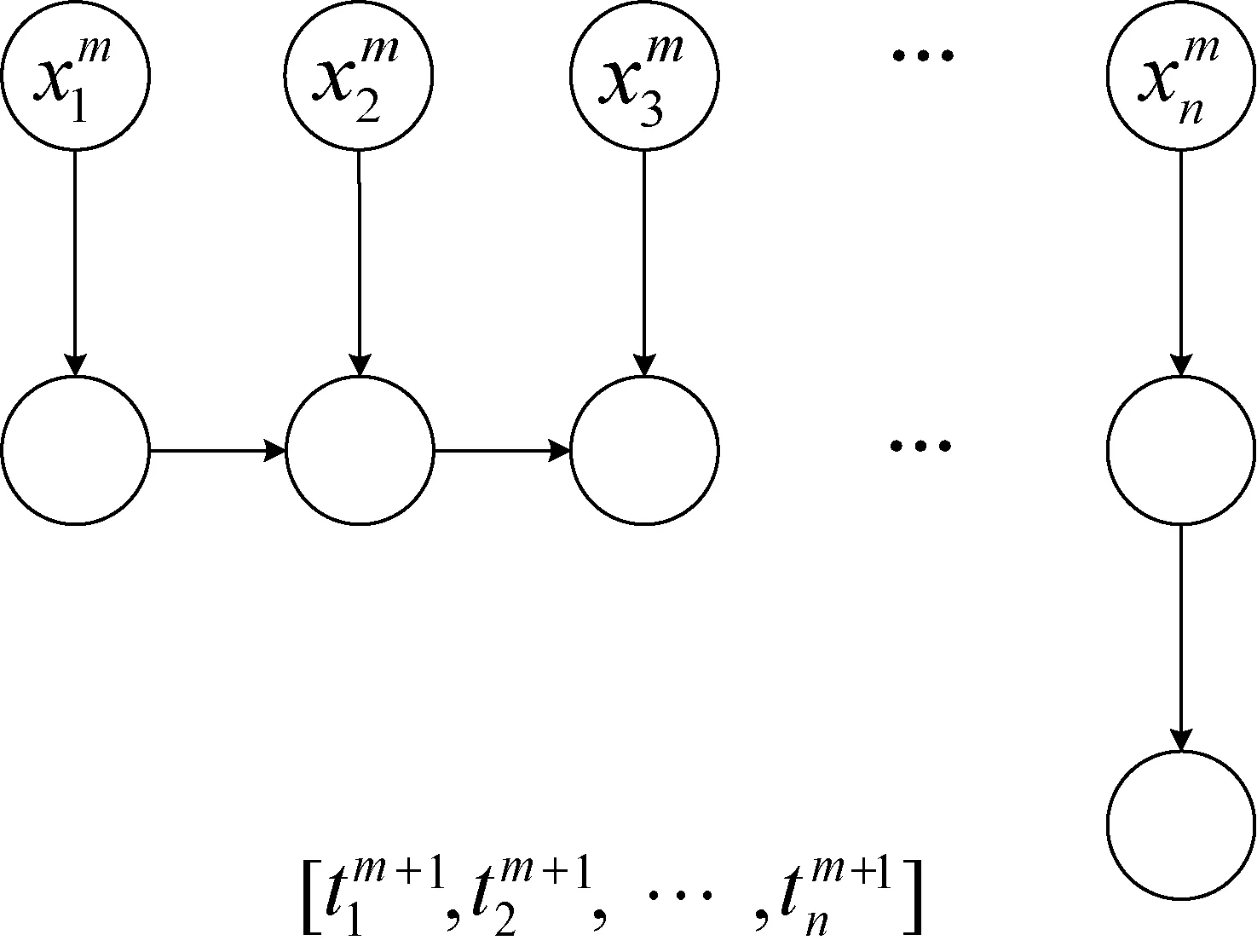
图2 LSTM静态预测
式(3)为Kalman滤波的状态方程:
(3)
式中:x(k)、y(k)分别表示公交车从初始站点到达第k站点所经历的时间和观测时间,u(k)表示公交车从第k个站点到达k+1站点的运行时间,A(k)、B(k)和H(k)分别为状态转移变量、输入变量、和测量值系数,在本次预测中设置A(k)=E,B(k)=E,H(k)=E。w(k)和v(k)分别为输入噪声和测量噪声,假设输入噪声和测量噪声是互不相关、均值为0的独立白噪声。
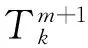
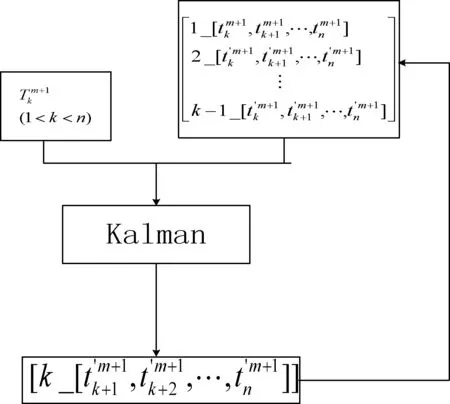
图3 Kalman滤波动态调整
以下是算法步骤:
(1) 经训练的LSTM模型:LSTM()。
(2) 利用第m车次的元数据静态预测第m+1车次公交车到达各站点经历的时间,并将其作为基础时间序列存入二维数组B。
(3) 计算各站点预测值之间的时间差,存入数组u。
for k:= 1 ton-1 do
begin
u[k] ←B[1][k+1]-B[1][k]
end
(4) 初始化kalman滤波模型:kalman()。
(5) 动态调整过程:
for k:= 2 ton-1 do
begin
L←当前数组B中序列的数量
for i:= 1 to L do
begin
C[i] ← abs(Tm+1 k-B[i][k])
end
i1←数组C中最小值的索引
if i1 == k-1 then
for j:= 1 to n do
begin
if j<=k then
B[k][j]←B[k-1][j]
if j == k+1 then
if j > k+1 then
B[k][j]←B[k][j-1]+u[j-1]
end
else then
重新初始化kalman滤波:kalman()
for j:= 1 to n do
begin
if j <= k then
B[k][j]←B[k-1][j]
if j == k+1 then
if j < k+1 then
B[k][j]←B[k][j-1]+u[j-1]
end
return B[k]
end
其中k为站点编号,B[k]为公交车到达第k个站点时经调整后输出的时间序列。
3 评估指标
本次试验预测值与观测值的绝对偏差定义为:
x=|r-b|
(4)
式中:x是绝对偏差,r为公交车到达站点时间观测值,b为公交车到达站点时间预测值。
s1代表测试集中绝对偏差小于等于60的站点数,s2代表绝对偏差小于等于90的站点数,s3代表绝对偏差小于等于120的站点数,m是测试集中站点的总数。
准确率:
p1=(s1/m)×100%
(5)
p2=(s2/m)×100%
(6)
p3=(s3/m)×100%
(7)
式中:p1、p2、p3分别代表了预测值与观测值绝对偏差小于等于60秒、90秒、120秒的正确率。
均方误差:
(8)
平均绝对误差:
(9)
式中:n代表样本总数,k代表第k个站点。
由于当公交车到达第k站点时,如果其观测值与预测值的偏差较大,则对第k+1站点的预测会产生较大影响,因此本实验将第k+1站点的预测值参与指标计算和评估,当公交车结束一个车次时,便得到了所有站点的预测值。
综上所述,本文分别将长短时记忆递归神经网络的预测值和本文提出的模型的预测值的p1、p2、p3正确率,各站点均方误差,各站点平均绝对误差进行对比并作为评估指标。
4 实验结果及分析
为了验证上述模型的可行性,本文采用了青岛市468路公交车8月3日到8月28日的GPS数据对公交车经过的19个站点进行了时间预测。其中8月3日到8月21日的数据作为训练集,8月24日到8月28日的数据作为测试集,由于公交车在工作日和周六、周日的运行情况不同,所以本次实验没有将周六、周日的数据进行训练和预测。时间段的划分规则为:从早上6点到晚上21点,每30分钟划为一段。一个车次公交车要经过19个站点。本次实验中最终采取的是输入层节点为3,隐藏层节点为9,输出层节点为19的长短时记忆递归神经网络。所有训练集和测试集的样本均进行了归一化处理。
本文所使用模型的预测值的正确率如表1所示。静态预测模型LSTM的预测值的p1、p2、p3 正确率均高于SVM模型的正确率,静态预测模型经Kalman动态调整之后p1、p2、p3的正确率均有明显的提高,其中LSTN+Kalman模型的正确率高于SVM+Kalman模型预测正确率,这说明静态模型预测值的精度会影响Kalman动态调整的预测值精度。
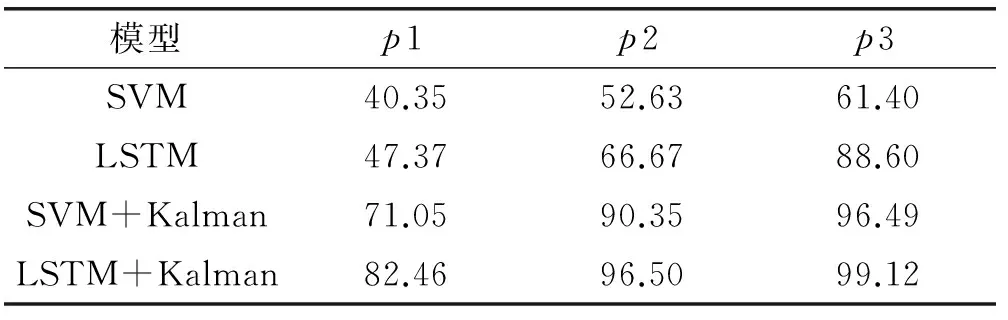
表1 各模型正确率 %
本文各模型各站点的均方误差如图4-图7所示。SVM静态预测模型各站点的均方误差变化幅度较大,LSTM静态预测模型各站点均方误差变化幅度相对较小,说明LSTM模型较SVM模型更好地拟合了公交车到达各站点所用时间变化趋势,而且LSTM模型预测值经Kalman模型动态调整之后,各站点均方误差均有降低,且较SVM+Kalman模型各站点均方误差更为平稳。
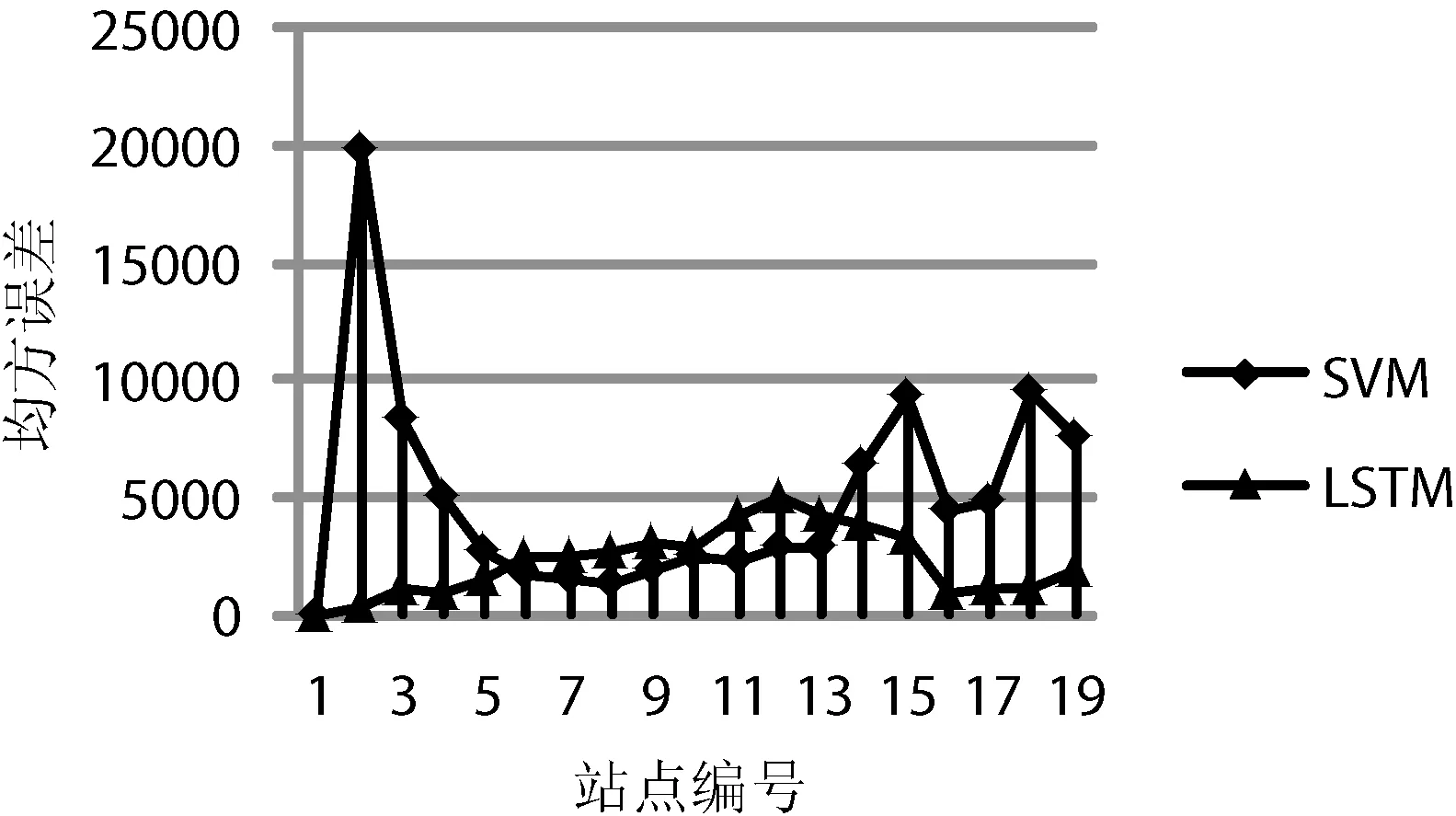
图4 静态模型各站点均方误差
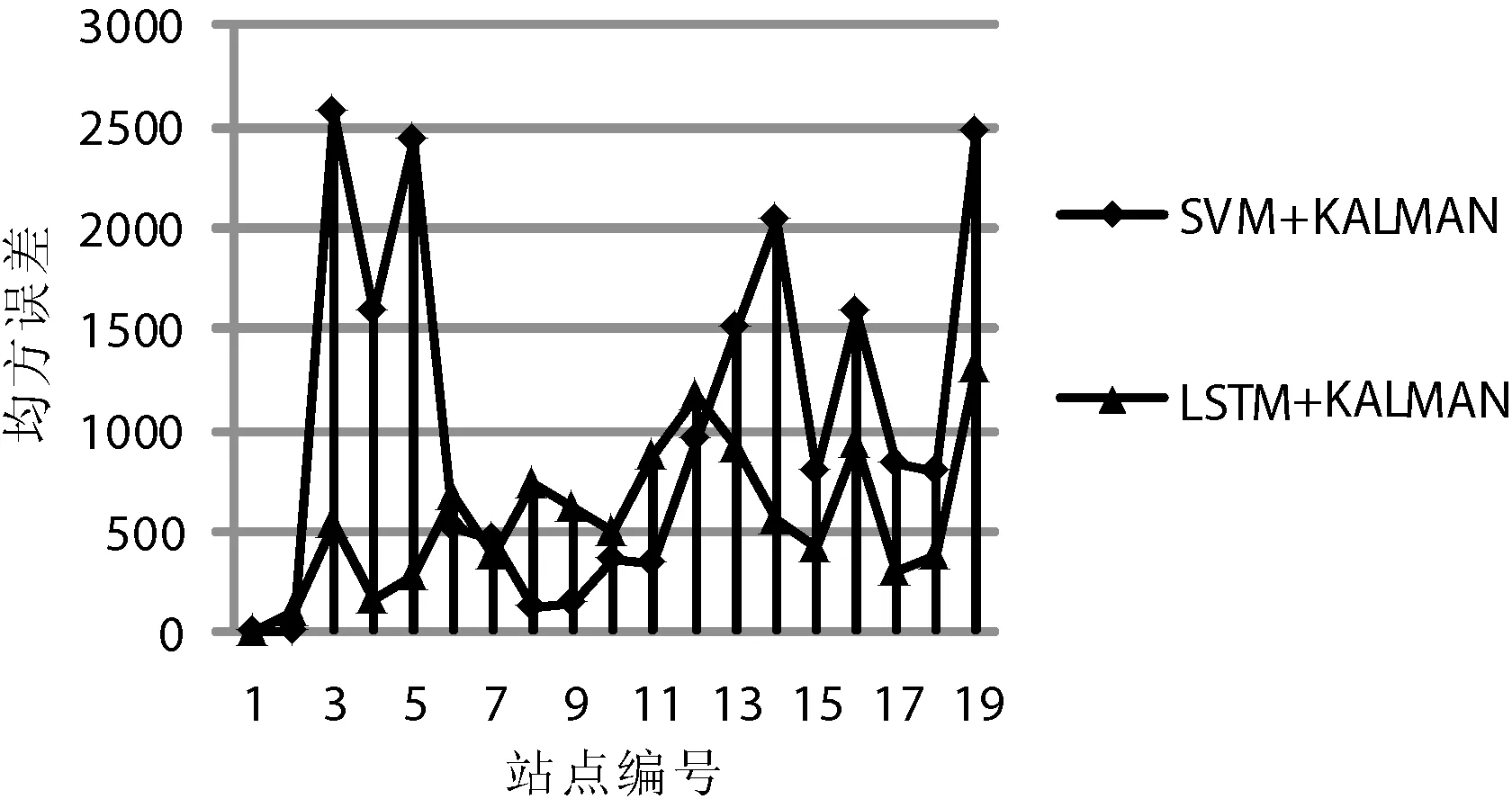
图5 动态调整模型各站点均方误差
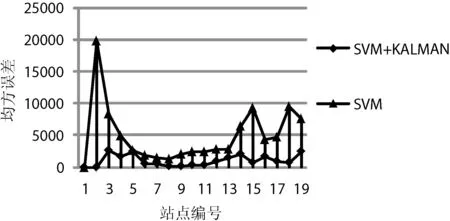
图6 SVM、SVM+KALMAN各站点均方误差
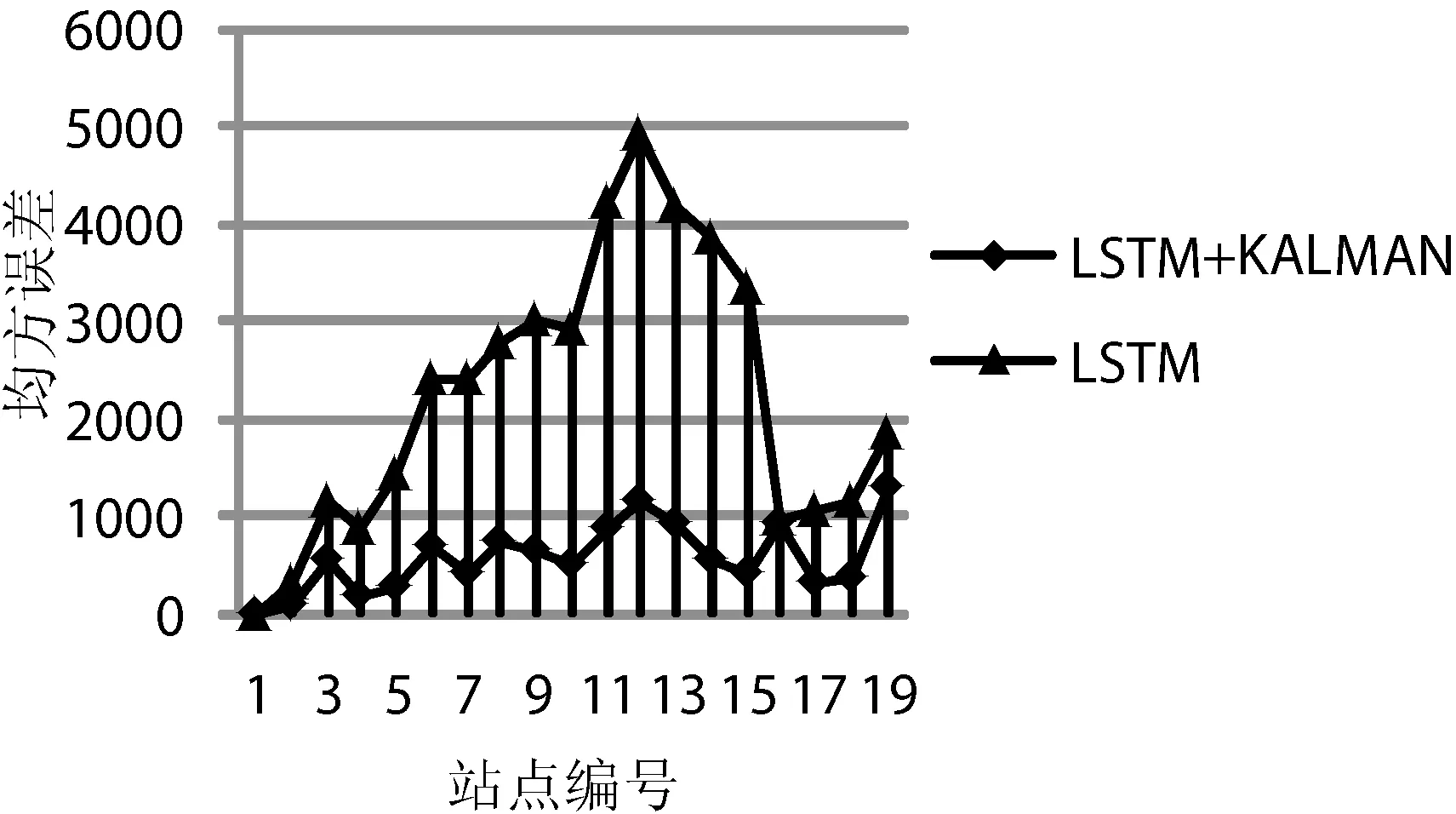
图7 LSTM、LSTM+KALMAN各站点均方误差
本文各模型平均绝对偏差如图8-图11所示。SVM各站点平均绝对偏差变化幅度较大,总体上SVM预测值的偏差要大于LSTM模型预测值的偏差,说明LSTM预测值的精度要高于SVM预测值的精度,LSTM+Kalman模型各站点平均绝对偏差变化趋势较SVM+Kalman模型平稳。
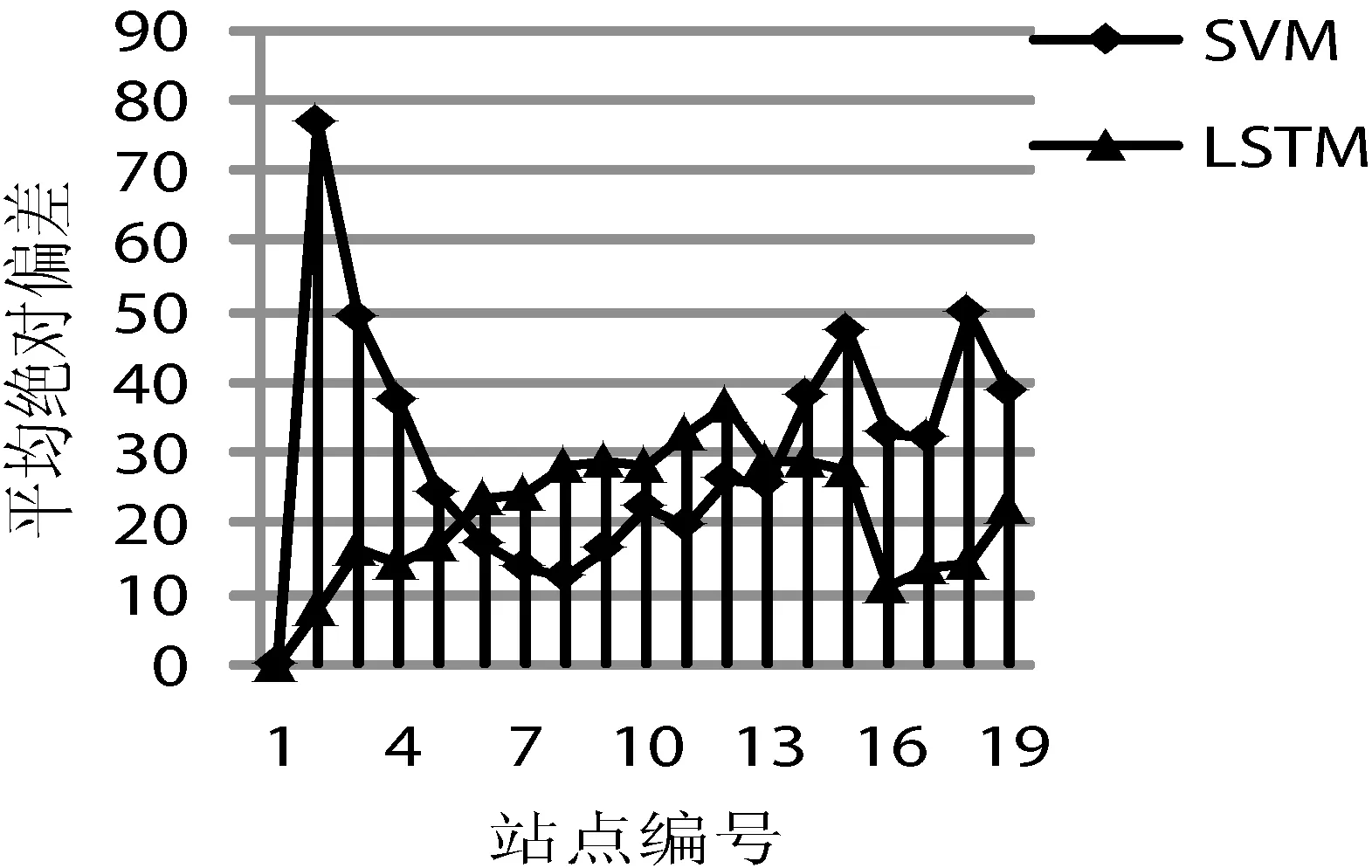
图8 静态模型各站点平均绝对偏差
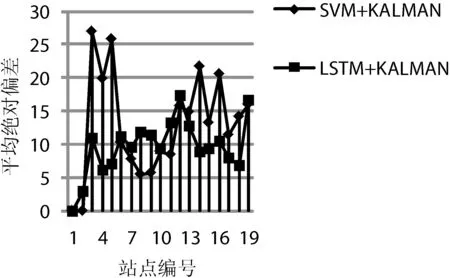
图9 动态调整模型个站点平均绝对偏差
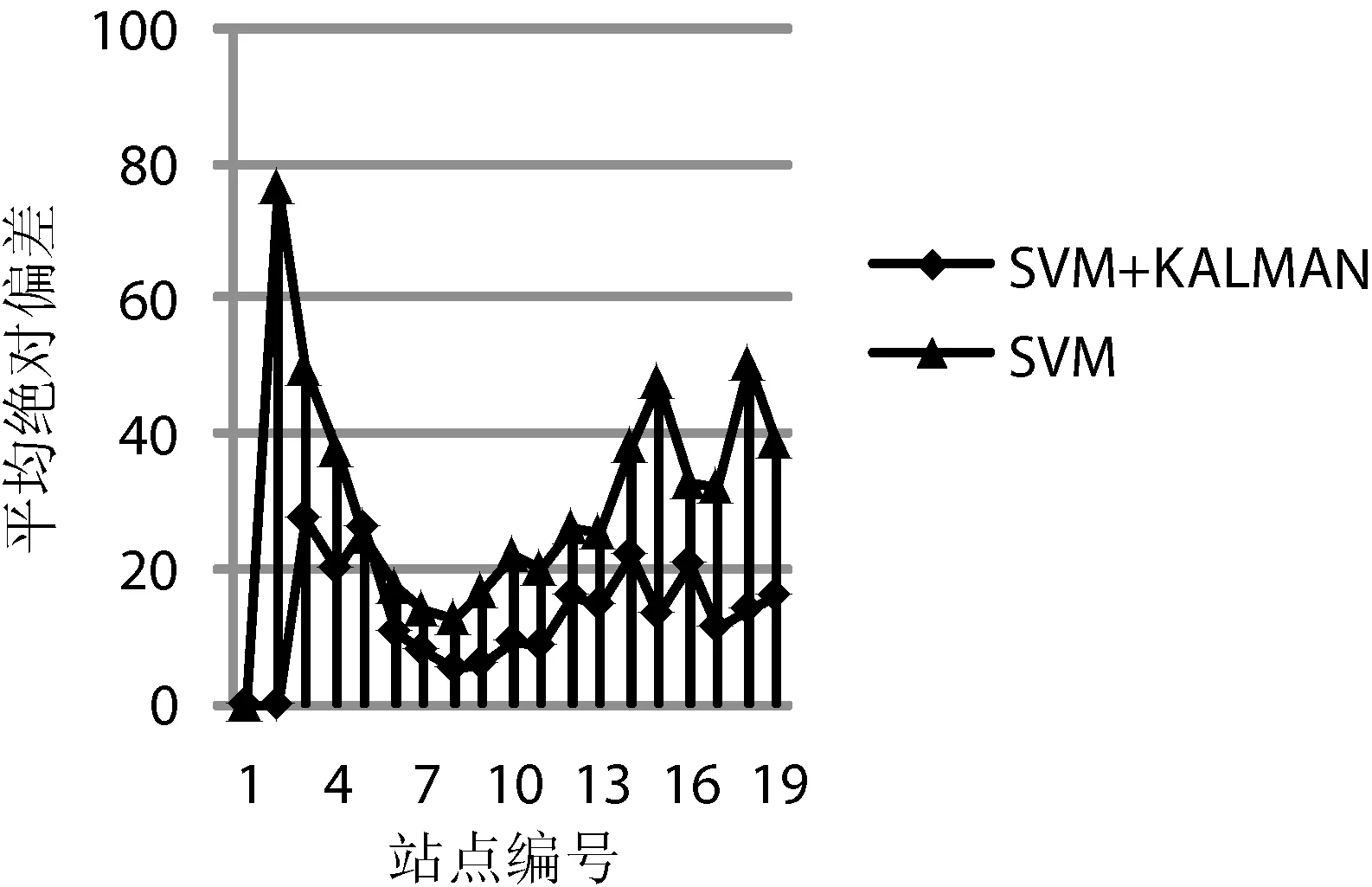
图10 SVM、SVM+KALMAN模型各站点平均绝对偏差
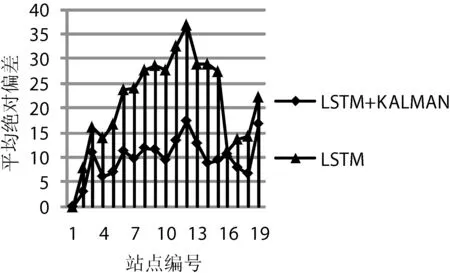
图11 LSTM、LSTM+KALMAN模型各站点平均绝对偏差
5 结 语
本文在讨论公交车辆到达时间预测模型和相关技术基础上,提出了基于LSTM神经网络和Kalman滤波的公交车到站时间预测模型。其中利用长短时记忆递归神经网络为静态预测模型,它从历史数据中总结出规律。Kalman滤波模型作为动态模型,结合观测数据在长短时记忆递归神经网络预测值的基础上进行动态调整。本文将LSTM+Kalman、LSTM、SVM、LSTM+Kalman模型预测值分别进行比较。实验结果证明,静态模型LSTM的预测值的正确率、均方差、平均绝对偏差均优于SVM静态模型,且LSTM+Kalman模型的预测精度最高。
[1] Jeong R,Rilett L R.Prediction Model of Bus Arrival Time for Real-Time Applications[J].Transportation Research Record Journal of the Transportation Research Board,2005,1927(1):195-204.
[2] 陈鹏.基于BP神经网络的公交智能实时调度模型研究及系统实现[D].北京:北京交通大学,2008.
[3] 于滨,杨忠振,林剑艺.应用支持向量机预测公交车运行时间[J].系统工程理论实践,2007,27(4):160-164.
[4] Chen M,Liu X,Xia J.Dynamic Prediction Method with Schedule Recovery Impact for Bus Arrival Time[J].Transportation Research Record Journal of the Transportation Research Board,2005,1923(1):208-217.
[5] 于滨,杨忠振,曾庆成.基于SVM和Kalman滤波的公交车到站时间预测模型[J].中国公路学报,2008,21(2):89-92.
[6] Chien I J,Ding Y,Wei C.Dynamic Bus Arrival Time Prediction with Artificial Neural Networks[J].Journal of Transportation Engineering,2002,128(5):429-438.
[7] 计晓昕,关伟.组合非参数回归和卡尔曼滤波的公交车到站时间预测[J].科学技术与工程,2013,13(32):9581-9586.
[8] Hochreiter S,Schmidhuber J.Long Short-Term Memory[J].Neural Computation,1997,9(8):1735-1780.
[9] Gers F A,Schmidhuber J,Cummins F.Learning to forget:continual prediction with LSTM[J].Neural Computation,2000,12(10):2451-2471.
[10] Grewal M S,Andrews A P.Kalman Filtering:Theory and Practice Using Matlab[M].New York:John Wiley,Sons,2001.
