一种基于平行坐标系的流转数据可视化方法
2018-05-03张元鸣高亚琳蒋建波陆佳炜
张元鸣 高亚琳 蒋建波 陆佳炜 徐 俊 肖 刚
(浙江工业大学计算机科学与技术学院 浙江 杭州 310023)
0 引 言
随着信息技术在企业、银行、政务等各领域的广泛应用,尤其是近年来软件以服务的方式被使用,越来越多的共性业务系统依托于公共的软件服务平台,如“专业技术评审云政务平台”[1]、“快递云管理平台”[2]等。这些平台根据业务规则所产生的数据也越来庞大,其中一类比较重要的数据是流转数据。例如,政务云中的流转数据就包括审批材料、来源部门、去向部门、审批层级、审批时间、审批人、审批结果等信息。这些流转数据蕴含着丰富的有价值的知识,如通过流转数据可以知道材料审批在全省各部门之间的总体情况,包括材料的提交和审批的时间和结果等,以及材料报送及时性、材料审批效率、材料相对集中的部门等。挖掘和掌握这些潜在规律有助于了解材料审批瓶颈、优化审批流程、准确了解审批进程等。
如何有效地可视化流转数据是数据可视化分析的一个重要内容。由于流转数据的来源、流转部门具有不确定性和动态性,流转层级也较高且动态变化,附加在其上的信息也非常丰富,因此寻求一种良好的可视化方法成为一个关键。
平行坐标系是一种基于二维图形表达高维数据的可视化技术,能够方便地将复杂的高位数据在平面图形中展示出来。该技术于1985年由Inselberg提出,并随后被其他研究者深入研究,并作为一种重要的可视化技术被应用于疾病诊断[3-4]、过程控制[5]、基因数据表达[6]等方面,为用户提供了直观的可视化结果。
针对流转数据的特点,本文提出了一种通用的基于平行坐标系的流转数据可视化方法,将流转数据的中间环节映射为平行坐标系轴上的点,将流转数据的关系映射为平行坐标系轴之间的折线。通过将流转数据预处理,转化为适合于平行坐标系可视化的数据模型,并基于Spark框架实现了对海量流转数据的加速处理、结果聚类及可视化交互式技术等。不仅提高了流转数据可视化分析性能,而且增强了可视化的效果。实验表明,该方法能够有效地对流转数据进行可视化,为可视分析流转数据中蕴藏的知识提供了一种有效途径。
1 相关研究
平行坐标系自被提出后被国内外研究者广泛的研究和应用,并在原有基础上进行了改进和增强,主要集中在聚类分析、可视化映射、可视化交互。
在平行坐标系应用方面,董重等[7]提出了基于平行坐标系的多变元时序数据可视化方法,通过时间维分段方法对数据进行处理,并在气象科学数据中进行了验证。徐永红等[8]基于简单贝叶斯公式计算属性值及区间的点得分,建立平行坐标系和相应分类,并将该方法应用到肝功能异常数据集中,以揭示数据的内在联系。雷君虎等[9]提出了利用PCA主成分分析方法对高维数据进行降维,将降维后的数据通过平行坐标系可视化,并应用于香精香料指纹图谱数据。胡俊[10]等将平行坐标系应用于UCI数据库的可视化,以挖掘研究与应用的关系。
在平行坐标系折线聚类方面,陈谊等[11]通过平行坐标系折线的聚类,来辅助医生对可视化方式对客户情况进行分析。Zhou等[12-13]提出了基于视觉聚类方法增强平行坐标系的可视化效果,并进一步通过叠加半透明线段增强重要的信息。刘芳等[14]利用自组织映射对原始数据进行分类,然后利用引力场原理对每个类中折线进行聚类,通过设置不透明及交互操作等手段对可视化结果进行增强。陈谊等[15]将交互式分析及聚类分析运用到平行坐标可视化,以加快数据挖掘进程。徐永红等[16]提出了一种基于多元数据平行坐标系表示的贝叶斯可视化分类方法,用平行坐标可视化原始数据,通过贝叶斯算法处理原始数据,达到较好的可视化和分类效果。翟旭君等[17]针对多维数据的大数据集的有效显示问题,提出通过直观聚类集交互技术进行聚类、分层平行坐标区分模糊数据,使得隐藏信息容易被发现。
在平行坐标系可视化增强方面,Johansson等[18]提出了通过构建聚簇,并用自定义的转换函数高亮聚簇信息及得到数据的不同信息,以解决海量数据可视化中不隐藏原本信息的问题。Dasgupta等[19-20]提出了基于量化不同视觉结构的屏幕空间度量的模型,能够根据用户的偏好进行度量和优化显示。Paulo等[21]提出了一种支持多视图协同的平行坐标系可视化工具,让用户通过相同的数据集提供不同的视图更好地理解数据集。聂俊岚等[22]将平行坐标与交互操作应用到传递函数中,通过引入平行坐标主维度概念,有效地降低高维传递函数设计的复杂度。郭翰琦等[23]提出通过设置传递函数、定义数值到颜色和透明度等可视化特征,优化可视化生成图像效果。
在平行坐标系可视化交互方面,Chen等[24]提出了基于平行坐标和增强环的多维数据可视化方法,以交互式方式对数据进行初步统计,减少数据集大小及更改显示比例来优化可视化效果。Yuan等[25]提出了一个在平行坐标系中集成散点图的方法,该方法将两个相邻的坐标轴转换为散点图,并通过缩放将多个轴转换为单个子图,通过刷技术实现无需切换的折线选择。Guo等[26]提出通过交互操作对平行坐标中的数据进行聚类操作,允许用户动态地调整聚簇参数来达到最优化,以聚焦于感兴趣的区域。
与现有关于平行坐标系的研究相比,本文提出了一种针对流转数据的可视化方法,能够将数据的流转过程方便地投影到平行坐标系上,将其可视化过程抽象为流转数据集、矩阵模型、平行坐标系可视结构三个主要模型,具有较强的通用性。此外,本文基于Spark并行计算框架实现了对海量流转数据的并行加速处理、结果聚类及可视化交互式技术,提高了平行坐标系可视化的性能,并增强了平行坐标系可视化效果,适用于海量流转数据的可视化。
2 基于平行坐标系的流转数据可视化模型
借鉴Card等[27]提出的可视化参考模型,设计基于平行坐标系的流转数据可视化模型。该模型主要包括流转数据集、矩阵模型、平行坐标系可视结构三个主要模型,通过转换算法将流转数据集转换为矩阵模型,通过绘制算法得到平行坐标系可视结构。其可视化流程如图1所示。

图1 基于平行坐标系的流转数据可视化流程
2.1 流转数据可视化模型
先对流转数据集进行统一的描述,解决流转数据格式多样化问题,便于对流转数据进行一致性处理。
定义1流转数据集TDS为流转数据项t的集合,表示为:
TDS={t|t=
式中:t是一个四元组;tid是数据项的标识;sender是数据项的发送方;receiver是数据项的接收方;profile是数据项的剖面信息,如初次流转日期、流转结果等。
定义2矩阵模型是对平行坐标轴、轴坐标、坐标间折线的抽象,分别表示流转数据的层次、流转来源或去向、流转关系,表示为一个m行n列的矩阵:
式中:
(1) 矩阵的元素aij(1≤i≤m, 1≤j≤n)对应平行坐标系的轴坐标,表示流转的发送方或接收方;
(2) 矩阵的每一列对应平行坐标系的一个轴线,表示部门的流转层次;
(3) 矩阵的每一行对应平行坐标轴线间的折线,表示流转关系。
定义3平行坐标轴可表示为一个三元组:
PCA=
式中:
(1)PCAid是平行坐标轴的标识;
(2)AxisPath={
定义4折线可表示为一个二元组:
BL=
式中:
(1)BLid是平行坐标折线的标识;
(2)LinePath={
定义5平行坐标可视结构表示一个完整的平行坐标系,表示为PCVS=<{PCA},{BL}>。
2.2 流转数据可视化过程
基于平行坐标系的流转数据可视化过程包括两个主要步骤:第一个步骤是流转数据转换,即将流转数据集转换为矩阵模型,该矩阵模型包含了流转数据及其之间的联系;第二个步骤是平行坐标系绘制,即根据矩阵数据模型绘制平行坐标系,以可视化方式显示。
2.2.1 流转数据转换算法
将流转数据集转换为矩阵模型的目的是构建一个流转数据的内部表示,为平行坐标系绘制提供数据驱动。首先,根据流转数据项的标识对流转数据集进行重组,将标识相同的流转项重组到一起,构建一个链表。其次,将链表的个数设置为矩阵的行数,迭代所有链表,对于第i个链表,将该链表中不与任意接收方相等的发送方作为起始发送方,并将其作为矩阵第i行的第1列元素。然后,将该发送方所对应的接收方作为矩阵模型第i行的第2列元素,将该元素作为中间值,迭代该链表。若链表中发送方存在与该中间值相等,将该发送方对应的接收方作为矩阵第i行的第下一列元素,将其作为中间值,直到链表中发送方中不存在与该中间值相等。矩阵中的每一行表示一条完整的数据流转过程,算法1给出了流转数据转换为矩阵模型的实现算法。
算法1流转数据转换算法
Input: TDS
Output : Matrix
1. Function Map(TDS={
2. Dim t, i, j, flag , Matrix;
3. t = getCombine();//combine the same element by tid
4. for(i=0;i 5. Matrix[i][0]=find(t[i][1]).firsts; //map firsts as Matrix’s the first 6. Matrix[i][1]=find(t[i][1]).firstr; //map firsts to r as Matrix’s the second 7. flag = find(t[i][1]).firstr; 8. for(j=0;j 9. m=2; 10. isContain(find(t[i][1].nexts)==flag){ //find s equals to flag 11. Matrix[i][m++] = find(t[i][1].nextr) //map s to r as Matrix’s the next 12. flag = find(t[i][1].nextr); 13. } 14. } 15. } 16. return Matrix; 17. } 2.2.2 平行坐标系绘制算法 根据转换得到的矩阵模型驱动平行坐标系的绘制,其绘制方法是:遍历矩阵模型的每一列,将该列映射为平行坐标系相对应的轴线,并将该列中非零元素及去重后的值设置为对应轴线上坐标的名称。根据该轴线上坐标名称的个数及轴长度设置刻度的横坐标及纵坐标。遍历矩阵模型的每一行,将该行的相邻两个元素关系映射为轴坐标之间的折线。算法2给出了平行坐标系可视结构的绘制算法。 算法2平行坐标系可视化绘制算法 Input:Matrix Output : PCVS 1. Function Draw(Matrix){ 2. Dim i,j, PCVS; 3. for(i=0;i< Matrix.collength;i++){ 4. draw PCAi{//map Matrix.coli to ParallelCoordinateAxisi 5. set PCVS.Axispathi; 6. } 7. } 8. for(j=0;j< Matrix.rowlength;j++){ 9. draw BLj{//map Matrix.rowj to BLj 10. set PCVS.LinePathj; 11. } 12. } 13. return PCVS; 14. } 当流转数据集体量比较大时,流转数据集的转换算法会受限于性能瓶颈。此外,大量的流转数据也会导致平行坐标系中折线的相互重叠,不易发现数据的流转规律。为此,给出一种基于Spark的流转数据并行可视化算法,并采用聚类思想对数据进行聚类,提高可视化效果。 Spark是一个基于内存计算的并行计算框架,于2009年由美国加州大学伯克利分校的AMPLab实验室开发。该框架具有MapReduce的优点,并将任务计算中间结果保存到内存中,提高了I/O性能。 Spark的核心是弹性分布式数据集(RDD),RDD是一种不可变的带分区记录集合,在迭代计算时可以高效的共享内存,目标是为基于工作集的应用提供一种抽象。RDD间的依赖关系分为窄依赖和宽依赖,窄依赖是指子RDD的分区只依赖父RDD的某个分区,宽依赖指子RDD的每个分区依赖父RDD的多个分区。并提供了转换和动作两类操作:转换是懒操作及延迟计算,执行后创建新的RDD;动作是真正触发程序的执行,结果是向程序返回普通值类型或向外部存储系统导出数据。 基于Spark的流转数据并行化可视化的流程如图2所示。首先,从HDFS读取流转数据集,并对该数据集分块,生成RDD1,RDD1通过combineByKey变换算子,按流转项的标识进行聚合计算,将标识相等的流转项汇聚为一个元素。该元素以流转项标识为key,以标识相等的流转项汇聚为链表并作为value,转化为RDD2。RDD2通过mapValues变换算子,对每个元素进行变换,使得每个元素中value按照流转顺序序列化,转化为RDD3。基于K-Means聚类思想对所有元素按照剖面信息进行聚类,例如可按流转日期、流转部门、流转类别等进行聚类,随机选择k个元素作为聚类中心,将当前聚类中心广播布至所有分区,计算其他元素与各个聚类中心的距离。并将元素分给距离最近的簇中心,重新计算各新类中心并更新聚类中心,迭代直到新类中心与原类中心的距离小于指定阈值有可能出现簇中心不再变化的情况或者迭代次数达到设定值。将同一个类的结果采用相同的颜色绘制折线,不同类之间采用不同颜色的绘制折线。 图2 基于Spark框架的流转数据并行化处理流程 算法3给出了以上处理流程的具体实现,第1~3行是Spark集群环境的初始化,第4~6行是读取流转数据集并对该数据集进行分块,并按流转项的标识进行聚合计算,将标识相等的流转项汇聚到一起。然后对每个元素进行变换,使得元素中流转项按顺序排列,第7行是选取k个不同的元素作为初始聚类中心,第8~23行计算各元素到聚类中心的距离,并更新聚类中心,直到满足收敛条件或最大迭代次数。 算法3基于Spark框架的流转数据并行处理算法 Input: TDS Output : Matrix 1. Function ParallelDeal(TDS){ 2. val conf = new SparkConf() 3. val sc = new SparkContext(conf) 4. val rdd1 = sc.textFile(TDS).map(x=>(x.split(″,″,2)(0),x.split(″,″,2)(1))) 5. val rdd2 = rdd1.combineByKey(List(_), (x:List[String],y:String) => y::x , (x:List[String],y:List[String]) => x:::y).sortByKey(true) 6. val rdd3 = rdd2.mapValues() 7. val centrio = selectCentriole(rdd3,k) //Select thekcenter points 8. do{ 9. res = centrio; 10. foreach(s in rdd3){ 11. thdistance = max; 12. foreach(c in centrio){ 13. distance = calculateDistance(s,c) 14. if(distance>thdistance){ 15. distance = thdistance 16. } 17. } 18. list.add(s) 19. } 20. newres = relocateCentrio(list,res,k) //reset the center point 21. }while(!isCentrio(newres,res)) 22. return list; 23. } 本文采用一个包括3个节点的小型集群作为实验平台,每个节点配置相同,都具有16 GB内存和8核的处理器,集群中已部署Spark-2.0.1-bin-hadoop2.7和Hadoop-2.7.3稳定版,Java为JDK1.8.0(Linux版),操作系统为Ubuntu16.04.2 LTS版本。 流转数据集来自某省高级专业技术资格(职务)云管理平台中的审批流转数据[28]。审批流转数据包括材料申报编号、材料发送单位、材料接受单位、材料基本信息、发送时间、发送结果等信息。审批流转数据集共有30 225 159个流转数据项,文件大小为2.5 GB,已存储到机群的HDFS中。下面从平行坐标系可视化效果及可视化性能两方面进行实验与分析。 基于平行坐标系的审批流转数据可视化结果如图3、图4所示。 图3 流转数据的平行坐标可视化图 图4 聚类效果平行坐标可视化图 图3给出了不包含聚类的平行坐标可视化结果,图中每个坐标轴表示流转的部门层级,坐标轴上的点表示流转单位,折线表示流转关系。该平行坐标系可视化从宏观与微观角度展示审批过程中流转过程及各个审批部门间的相互关系,用户可以选择感兴趣的流转过程,可交互式地给出相对应的流转数据在不同部门之间流转过程的详细信息,能够更方便地对流转过程进行分析和管理。 图4为基于聚类的平行坐标系流转数据可视化结果。该结果按流转层级对流转项进行聚类,不同的聚类结果采用不同颜色(不同的灰度表示)进行绘制,解决了折线相互重叠的问题,提升了可视化效果,更易发现相似特征的流转数据隐含信息。从图中可知,该数据集得到的聚类结果中,灰色①线条表示流转层级较低的流转项,流转层级为2(流转项只经过2层的流转过程),浅灰色②和黑色③线条表示流转层级较高,流转层级为5,深灰色④线条表示流转层级最高的流转项,流转层级为6;在所有流转项中,流转层级为6的流转项数据量相对比较多,流转层级为2的流转项数据量相对比较少。基于聚类的平行坐标系流转数据可视化效果可以清晰直观地得到相同流转层级的流转项。 为了测评基于Spark的并行处理算法的性能,设置了3种不同大小的流转数据集:(1) 流转数据10 075 053项(共854 MB);(2) 流转数据20 150 106项(共1.67 GB);(3) 流转数据30 225 159项(共2.5 GB)。 图5对比了单节点与集群环境对以上不同大小数据集的处理性能,单节点即只采用一个节点分别对3种不同大小的数据集进行处理。而集群则采用三个节点分别对3种不同大小的数据集进行处理,每个节点使用8个处理核心。从图中可以看出,随着数据量的增大,单节点和集群环境下处理时间均呈线性增加趋势。但是,单节点情况下增幅非常大,集群环境下增幅相对比较缓慢,数据量相同情况下,集群环境处理时间大约为单节点处理时间的20%。这是因为集群环境下提供了更多的计算资源且Spark具有内存迭代计算的特点。由此可见,集群环境比单机情况下可视化性能更高,可以适应体量的流转数据。 图5 数据量与处理时间关系 图6给出了集群环境下不同处理核数的处理性能,将集群总核数分别设为3核、6核、12核、18核、24核。设置的流转数据集为30 225 159项(2.5 GB)。从图中分析可知,随着工作核数的增加,并行处理时间呈线性减少趋势。其中,当工作核数从3核扩充到6核时,处理时间的减少趋势比较明显,当核数从3核数增加到24核时,处理效率提升了2.35倍,相比核数倍数增加,处理效率并未呈同倍增长趋势。这是因为在Spark集群环境下,节点之间存在通信开销、资源分配不均等问题。总体来说,集群环境下处理大规模数据集时,随着工作核数的增加,可并发执行的任务随之增加,处理性能也随之提升。 图6 工作核数与处理时间关系 为了分析流转数据中规律性知识,本文提出了一种基于平行坐标的数据流转的可视化方法。该方法通过流转数据的转换算法及平行坐标系可视化绘制算法将流转数据集映射到平行坐标系中,并结合Spark框架提出并行可视化算法,解决了海量流转数据可视化性能问题,并结合聚类算法增强了平行坐标系的视觉效果。实验结果表明,该方法能有效地可视化流转数据,便于对流转进行可视化分析,有助于发现流转数据的规律性知识。 [1] Zhang Y,Ni K,Lu J,et al.DOGCP:A Domain-Oriented Government Cloud Platform Based on PaaS[C]//IEEE,International Conference on Cyber Security and Cloud Computing.IEEE,2016:115-120. [2] 王霞.基于云计算的快递物流管理系统的研究[D].大连海事大学,2015. [3] 谭桂龙,陈谊.基于平行坐标的信息可视化方法的应用研究[J].食品科学技术学报,2008,26(2):75-80. [4] 徐永红,高直,金海龙,等.平行坐标原理与研究现状综述[J].燕山大学学报,2008,32(5):389-392. [5] Albazzaz H,Wang X Z.Historical data analysis based on plots of independent and parallel coordinates and statistical control limits [J].Journal of Process Control,2006,16(2): 103-114. [6] Tao Y,Liu Y,Friedman C,et al.Information Visualization Techniques in Bioinformatics during the Postgenomic Era[J].Drug Discovery Today Biosilico,2004,2(6):237-245. [7] 董重,魏迎梅.运用平行坐标系的多变元时序数据可视化方法[J].小型微型计算机系统,2015,36(10):2408-2411. [8] 徐永红,洪文学,高直,等.基于平行坐标的贝叶斯可视化分类方法[J].计算机工程与应用,2008,44(25):166-169. [9] 雷君虎,杨家红,钟坚成,等.基于PCA和平行坐标的高维数据可视化[J].计算机工程,2011,37(1):48-50. [10] 胡俊,黄厚宽,高芳.一种基于平行坐标的度量模型及其应用[J].计算机研究与发展,2011,48(2):177-185. [11] 陈谊,谭桂龙.多维数据的信息可视化方法及应用研究[J].系统仿真学报,2008(S1):327-329. [12] Zhou H,Yuan X,Qu H,et al.Visual Clustering in Parallel Coordinates[J].Computer Graphics Forum,2009,27(3):1047-1054. [13] Zhou H,Cui W,Qu H,et al.Splatting the lines in parallel coordinates[C]//Eurographics/IEEE-Vgtc Conference on Visualization.The Eurographs Association & John Wiley & Sons,Ltd.2009:759-766. [14] 刘芳,田凯,周志光,等.基于SOM和引力场聚类的金融数据可视化[J].计算机辅助设计与图形学学报,2012,24(4):435-442. [15] 陈谊,蔡进峰,石耀斌,等.基于平行坐标的多视图协同可视分析方法[J].系统仿真学报,2013,25(1):81-86. [16] 徐永红,洪文学.点得分平行坐标可视化分析方法[J].燕山大学学报,2008,32(5):440-444. [17] 翟旭君,李春平.平行坐标及其在聚类分析中的应用[J].计算机应用研究,2005,22(8):124-126. [18] Johansson J,Ljung P,Jern M,et al.Revealing Structure within Clustered Parallel Coordinates Displays[C]//Information Visualization,2005.INFOVIS 2005.IEEE Symposium on.IEEE,2005:125-132. [19] Dasgupta A,Kosara R.Pargnostics:screen-space metrics for parallel coordinates[J].IEEE Transactions on Visualization & Computer Graphics,2010,16(6):1017-1026. [20] Dasgupta A,Kosara R,Gosink L.Meta parallel coordinates for visualizing features in large,high-dimensional,time-varying data[C]//Large Data Analysis and Visualization.IEEE,2012:85-89. [21] Godinho P I A,Meiguins B S,Meiguins A S G,et al.PRISMA-A Multidimensional Information Visualization Tool Using Multiple Coordinated Views[C]//Information Visualization,2007.IV’07.International Conference.IEEE,2007:23-32. [22] 聂俊岚,刘益萌,张继凯,等.基于平行坐标主维度的多变量传递函数设计方法[J].计算机辅助设计与图形学学报,2015(12):2340-2349. [23] 郭翰琦,袁晓如.体数据可视化传递函数研究[J].计算机辅助设计与图形学学报,2012,24(10):1249-1258. [24] Chen Y,Cheng X,Chen H.A multidimensional data visualization method based on parallel coordinates and enhanced ring[C]//International Conference on Computer Science and Network Technology.2011:2224-2229. [25] Yuan X,Guo P,Xiao H,et al.Scattering points in parallel coordinates[J].IEEE Transactions on Visualization & Computer Graphics,2009,15(6):1001-1008. [26] Guo P,Xiao H,Wang Z,et al.Interactive local clustering operations for high dimensional data in parallel coordinates[C]//IEEE Pacific Visualization Symposium Pacificvis.IEEE,2010:97-104. [27] Card S K,Mackinlay J D,Shneiderman B.Readings in information visualization-using vision to think[C]//Series in Interactive Technologies.Morgan Kaufmann Publishers Inc.1999. [28] 张元鸣,陈苗,陆佳炜,等.非结构化表格文档数据抽取与组织模型研究[J].浙江工业大学学报,2016,44(5):487-494.3 基于Spark的流转数据并行可视化
3.1 Spark并行框架
3.2 并行可视化算法

4 实验与分析
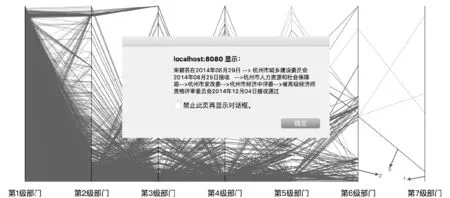
4.1 平行坐标系可视化效果

4.2 绘制性能

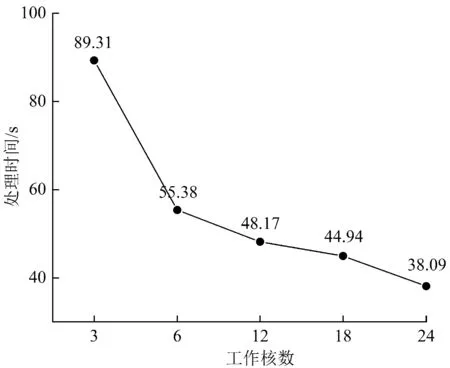
5 结 语
