多自由度振动环境下惯组非线性传递特性研究
2018-05-03付玮丁镇军边学鹏
付玮,丁镇军,边学鹏
多自由度振动环境下惯组非线性传递特性研究
付玮,丁镇军,边学鹏
(北京强度环境研究所,北京 100076)
惯组作为飞行器姿控系统的传感器,其局部安装结构的传递特性的测量精度直接关系到导航精度。目前,惯组普遍使用减振器进行隔振,而减振器都呈现出较强的非线性特征。为了考察惯组在不同工况下的传递特性,将惯组简化为六自由度Duffing模型,推导了基础激励下系统的运动微分方程,并用龙格−库塔法对方程进行求解,分析了自由衰减振动和强迫振动下不同工况的系统传递特性。结果表明,多自由度激励比单自由度激励工况得到的系统传递特性的频率和幅值都低。考虑到惯组真实的使用环境,应当在多自由度振动环境下进行传递特性试验。
多自由度;惯组;非线性;传递特性
0 引言
惯组导航系统用于测量飞行器运动姿态。为了提高惯组的力学环境适应性,通常在惯组敏感本体与安装基础之间采取减振措施。而减振环节的插入改变了惯组小系统原有的刚性传递特性。传递特性是姿控系统设计的重要参数,工程上一般通过传递特性试验获取。惯组由3个角速度陀螺和3个加速度计构成,从而获得反映惯组安装处的6个自由度的运动量,通过传递特性矩阵可以得知飞行器的姿态。目前测量惯组小系统传递特性的方法是通过单自由度激励试验,分别获取每个自由度的传递特性,这个过程没有考虑到惯组多自由度间的耦合现象。文献[1-3]将多点减振惯组简化为线性多自由度模型,并进行了仿真分析,针对各自由度间可能出现的耦合现象,通过合理的减振器布局实现解耦。但试验与研究结果表明,减振器都呈现较强的非线性特征[4],线性多自由度系统已经不能准确描述惯组小系统各自由度间的耦合特性。
为了研究惯组在多自由度振动环境下的非线性传递特性,本文将惯组小系统简化为六自由度非线性弹簧−质量系统。根据非线性系统建模的研究经验[5],选择Duffing模型可较好地表征其非线性特性[6-7]。考虑惯组真实使用环境,建立了多自由度振动环境下的动力学方程。使用数值积分方法,分别对惯组在自由衰减振动和强迫振动环境下的结构动力学响应特性和传递特性进行分析,以获得各自由度振动环境及减振器非线性特性对惯组的结构动力学响应和传递特性的影响规律。
1 六自由度运动微分方程的建立
本文选取比较常见的四减振器外减振模型,4组完全相同的橡胶减振器安装在惯组敏感本体的4个角且位于同一平面,惯组质心位于该平面。减振器两端分别连接惯组本体和惯组安装基础。橡胶减振器具有立方刚度和黏性阻尼的特性。通过上下2个减振器夹紧惯组本体的支耳,减振器外沿和凸起分别提供垂直和平行于减振器安装平面的刚度。由于这2个方向的减振器刚度不同,将4组减振器转化为8个弹簧阻尼系统,如图1所示,其中:立方体是惯组本体;虚线框内是弹簧阻尼系统;1~4号提供轴方向的刚度,5~8号提供平面的刚度。将各弹簧阻尼系统的变形量投影到坐标轴上,如图2所示,可对惯组本体建立几何方程和平衡方程。

图1 六自由度基础激励模型

图2 减振器变形示意
1.1 几何方程
假设相邻减振器之间距离为2,惯组本体质量为,重心与几何中心重合,绕3个轴的转动惯量都为。在基础处施加运动激励,其中沿、、轴的线运动分别为01、02、03,绕、、轴的角运动分别为01、02、03,惯组本体响应对应的线/角运动分别是1、2、3、1、2、3,令惯组本体对安装基础的相对运动分别为r1、r2、r3、r1、r2、r3,有:
ri= y–0i,riθ–0i,=1, 2, 3。 (1)
令惯组本体与安装基础在8处弹簧阻尼系统的相对位移分别为1~8,则几何方程为

1.2 平衡方程
各处弹簧阻尼系统的弹性恢复力为

式中:1、2分别为向和向的减振器黏性阻尼;11、21分别为向和向的减振器线性刚度;13、23分别为向和向的减振器立方刚度。
对惯组本体进行受力分析,其平衡方程为
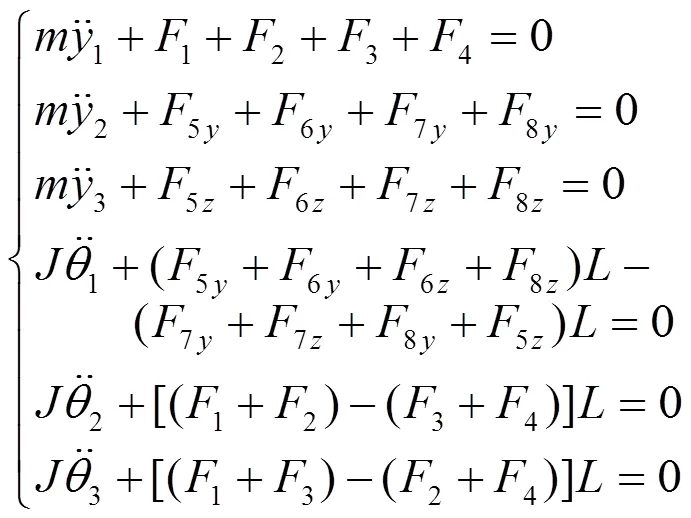
此处模仿线性系统定义,1~6分别为系统6个自由度的固有频率,1~6分别为系统6个自由度的阻尼比,令12=411/,22=32=421/,42=4212/,52=62=4112/,211=41/,222=233=42/,244=422/,255=266=412/,1=13/11,2=23/21。对于Duffing模型,此处增加了系数1和2,分别表示减振器向和向立方刚度系数与线性刚度系数的比值。联立式(2)~(4),得到惯组小系统六自由度运动微分方程为

其中:0={010203010203}T;r={r1r2r3r1r2r3}T;=diag(122232425262);=diag(211222233244255266);=diag(122211);
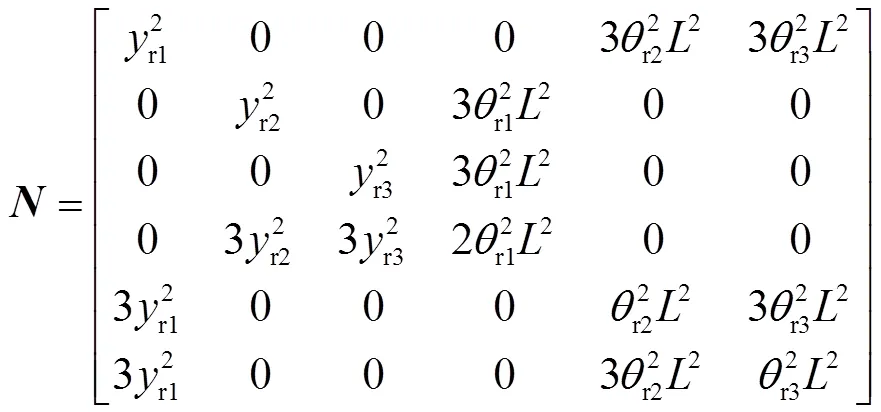
由式(5)可知:对于线性系统,1=2=0,方程退化为完全解耦的6个自由度的线振动方程与角振动方程,此时各自由度之间相互独立,这与文献[3]的结论一致;对于非线性系统,1,2≠0,矩阵的非对角元素不全为0,即不同自由度之间出现了耦合,此时各自由度之间不再独立。目前惯组的传递特性试验采用单自由度激励的方式,并没有考虑耦合项的影响,这与多自由度振动环境下获取的传递特性必然有所差别。为了评估2种激励方式造成的差别,需要对系统进行仿真分析。
进一步观察矩阵,发生耦合的是向线运动和绕、轴角运动,以及、向线运动和绕轴角运动,但这2组耦合之间是独立的。原因是减振器在垂直于安装平面的刚度影响1、2、3这3个自由度,平行于安装平面的刚度影响2、3、1这3个自由度,而这2个方向的刚度之间是正交的,相互独立。
2 不同工况下传递特性的仿真计算
式(5)是一个二阶微分方程组,可以变换为一阶微分方程组
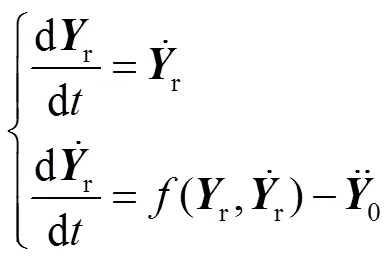
使用龙格−库塔法对式(6)的初值问题进行求解,进一步计算获取惯组本体的加速度响应。根据惯组小系统传递特性试验的经验,本文取线振动1=2=3=503rad/s,角振动4=5=6=754rad/s,阻尼比1=2=3=4=5=6=0.01,=0.01。由于橡胶减振器几乎都表现出“软特性”,所以这里假设1=2=-100。
2.1 自由衰减振动


图3 3个自由度自由衰减时域曲线
为了进一步研究多自由度和非线性对各自由度响应的影响,利用Hilbert变换来构建解析信号[8],获取系统幅值−频率特性,如图4所示。可以看出:随着振动幅值的衰减,振动频率都逐渐升高,这是典型的“软弹簧”的非线性特性;相同幅值水平下,多自由度振动的频率明显低于单自由度振动的,可见多自由度振动的非线性特性更加明显,说明不同自由度之间的相互耦合会增强系统的非线性特性。

图4 3个自由度幅值−频率曲线
2.2 强迫振动
为了获取系统在单自由度和多自由度振动环境下的传递特性,在惯组安装基础上施加随机运动输入。使用输入响应信号的自功率谱和互功率谱来估计系统的传递函数:
()=RE()EE()-1。 (7)
式中:EE()是输入信号的自功率谱;RE()是响应与输入的互功率谱。
随机振动输入信号功率谱选取40~150Hz的平谱,通过控制均方根值来确定激励的量级水平。计算了单独加载向线振动,绕、轴角振动以及同时加载多个自由度工况下的强迫振动,包括同时激励3个自由度、激励其中2个自由度以及单独激励1个自由度共7种工况。其中线加速度均方根值为400,角加速度均方根值为90000。利用式(7)对输入和响应的时域信号进行分析可以计算各工况下系统的传递特性,结果见图5,谐振频率与放大倍数统计值见表1。
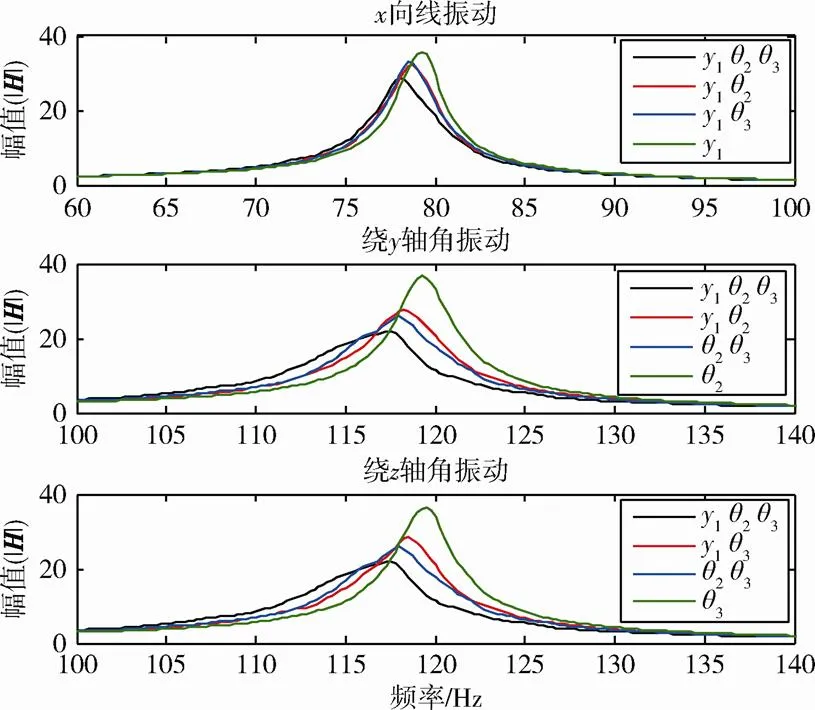
图5 随机振动传递特性幅值曲线

表1 传递特性谐振频率与放大倍数
从结果可以看出,相同量级水平下,随着激励自由度的增加,各自由度传递特性的谐振频率和谐振峰幅值都会降低,即激振自由度越多,相互之间耦合的影响越大,系统非线性特性越强。
传递特性的结果是姿控系统设计改进的重要依据,而姿控系统对惯组低频的谐振峰更加敏感,相同试验量级下,单自由度振动环境获取的惯组传递特性频率较高,这对姿控系统的设计不利。而多自由度振动环境更加接近真实的使用环境,获取的传递特性更加趋向“保守”。
3 结束语
将典型的四减振器惯组系统简化为六自由度Duffing模型,建立了基础激励下系统的运动微分方程;利用龙格−库塔法对惯组的非线性传递特性进行了仿真分析。结论如下:
1)刚度非线性造成了不同自由度之间的耦合,且发生耦合的是1、2、3这3个自由度以及2、3、1这3个自由度,这2组耦合之间是相互独立的;
2)多自由度工况相对于单自由度工况,加强了各自由度的非线性特征,且加载自由度越多,获得的非线性特性越明显;
3)惯组减振器几乎都表现出“软特性”,多自由度振动环境下的惯组传递特性频率更低,其结果用于姿控系统设计更加“保守”。
多自由度之间的耦合普遍存在。单自由度试验通过人为的方法实现了不同自由度之间的解耦,其结果必然会失真。考虑到传递特性是姿控网络设计的重要依据,且惯组真实工况更接近于多自由度振动环境,为获得更高的试验精度,建议在多自由度振动环境下对惯组进行传递特性试验。
[1] 章博, 任娟. 捷联惯组空间五点减振的振动耦合分析[J].宇航学报, 2015, 36(9): 1030-1035
ZHANG B, REN J. Coupling vibration analysis of spatial-five-point arrangement isolators for strapdown inertial navigation system[J]. Journal of Astronautics, 2015, 36(9): 1030-1035
[2] 刘攀, 刘和平, 张琛. 激光陀螺捷联惯组减振系统动力学特性研究[J]. 光学与光电技术, 2011, 9(5): 70-74
LIU P, LIU H P, ZHANG C. Research on dynamical characteristics of laser gyro strapdown IMU[J]. Optics & Optoelectronic Technology, 2011, 9(5): 70-74
[3] 姚建军. 捷联惯导系统不同隔振模式的比较[J]. 强度与环境, 2009, 36(2): 19-27
YAO J J. Contrast of different vibration isolation patterns used in strap-down inertial navigation system[J]. Structure & Environment Engineering, 2009, 36(2): 19-27
[4] 韩德宝, 宋希庚, 薛冬新. 橡胶减振器非线性动态特性的试验研究[J]. 振动工程学报, 2008, 21(1): 102-106
HAN D B, SONG X G, XUE D X. Experiment on nonlinear dynamic characteristics of rubber isolator[J]. Journal of Vibration Engineering, 2008, 21(1): 102-106
[5] WORDEN K, TOMLINSON G R. Nonlinearity in structural dynamics[M]. Bristol: Institute of Physics Publishing, 2001: 97-109
[6] 宋汉文, 王文亮, 傅志方. 橡胶减振器非线性动力参数辨识[J]. 复旦学报(自然科学版), 1998, 37(5): 607-612
SONG H W, WANG W L, FU Z F. Non-linear dynamic parameter identification of rubber absorber[J]. Journal of Fudan University, 1998, 37(5): 607-612
[7] 张鹏飞, 苏华昌, 吴家驹. 基于奇异值分解的惯性测量组合减振系统非线性刚度识别[J]. 导弹与航天运载技术, 2016(3): 68-72
ZHANG P F, SU H C, WU J J. Identification of nonlinear stiffness of inertial measurement unit with vibration absorber system based on singular value decomposition[J]. Missiles and Space Vehicles, 2016(3): 68-72
[8] HAHN S L. Hilbert transforms in signal processing[M]. Boston: Artech House, 1996: 95-117
(编辑:许京媛)
Nonlinear transfer characteristics of inertial measurement unit in vibration environment of multi-degrees of freedom
FU Wei, DING Zhenjun, BIAN Xuepeng
(Beijing Institute of Structure and Environment Engineering, Beijing 100076, China)
The inertial measurement unit (IMU) is the sensor of the attitude control system. The measurement precision of the transfer characteristics of the IMU directly affects its navigation accuracy. A damper is commonly used for the vibration isolation of the IMU, obviously with nonlinear characteristics. In order to analyze the transfer characteristics of the IMU under various working conditions, this paper simplifies the IMU as a Duffing cubic stiffness model with six degrees of freedom. The differential equations of motion under the base excitation is deduced, and solved by the Runge-Kutta method. The transfer characteristics of the system under free and forced vibration conditions are analyzed. It is shown that the frequency and the amplitude of the system under the working excitation condition of multi-degrees of freedom are lower than that under the excitation of single-degree of freedom. In the working environment of the IMU, the actual test should be carried out in the vibration environment of multi-degrees of freedom.
multi-degrees of freedom; IMU; nonlinearity; transfer characteristics
V241.6
A
1673-1379(2018)02-0123-05
10.3969/j.issn.1673-1379.2018.02.004
付玮(1986—),男,硕士学位,主要从事结构动力学的试验与仿真技术研究。E-mail: yuzhoufw@163.com。
2017-11-10;
2018-03-15
