基于二次线性最优理论的张拉整体结构主动振动控制

冯晓东 蒋 舸

(绍兴文理学院 土木工程学院，浙江 绍兴312000)

0 引言

张拉整体结构是一种轻质、网状、智能的空间结构体系，这类结构一般由若干个受压的杆元和受拉的索元组成.在过去的几十年时间里，国内外学者对张拉整体结构的主动振动控制进行了大量相关研究.刘锡良[1]发现张拉整体结构是一种可控的智能结构体系，并且这种新型空间结构极具发展前景.Djouadi等[2]将瞬时最优控制方法与非线性有限元方法相结合，解决了二类张拉整体结构在大变形下的主动振动控制问题.Kanchanasaratool等[3]提出了一种非线性约束的粒子模型，并且利用这种模型研究了张拉整体结构的反馈控制，同时在神经网络算法上发展了一种路径跟踪算法.Wijdeven等[4]采用约束优化法通过指定路径寻找到了结构的离散状态.Masi等[5]利用线性动力模型，提高了张拉整体结构的动态控制性能.Ali等[6]将理论分析和实验数据相结合，研究了张拉整体结构的动力特性和主动振动控制.Raja等[7-8]利用H2和H控制调节器讨论了在平稳激励和非平稳激励下张拉整体结构的振动控制问题.张沛等[9]以切线刚度矩阵的正定性为稳定判据，讨论研究了张拉整体结构的稳定条件.

考虑到张拉整体结构内部较为容易嵌入作动器或传感器，使得此类结构在形态控制上有巨大潜力，曾有学者建议将张拉整体结构作为抗震体系[10].但是要实现张拉整体结构作为抗震体系该目标，需要深入研究张拉整体结构在地震激励下的动态特性和振动控制.目前国内外关于张拉整体结构在地震激励下的动力响应或振动控制的相关文献较为稀少.因此对于张拉整体结构的SRC(Seismic-Response-Control)研究是十分有意义的.本文研究分析了二维张拉整体梁在地震激励下的动力响应和其相应的振动控制，并利用二次最优控制理论，分别采用三种控制方案，同时优化结构和作动器的布置，旨在使结构体系满足相应的稳定性、适用性和可靠性要求.

1 地震激励下动力计算模型和控制理论

1.1 动力响应

本节利用一个在平衡状态附近的线性动力模型，来描述地震激励下张拉整体结构的动力响应.结构某单元在预应力状态下的线性微分方程可描述如下：

(2)

在形成结构体系有限单元模型的过程中，需分别描述结构每个单元的质量矩阵和刚度矩阵[12].由此，通过每个独立单元在整体坐标系中的贡献，将其相加即得结构整体质量矩阵M和刚度矩阵Kb.

忽略式中的阻尼矩阵和地震激励，可以得到结构的模态方程：

(3)

式中：ω为结构的固有频率.由此可确定各模态质量和相应荷载：

(4)

(5)

式中：n为结构的自由度个数；r=1…n.

定义yr(t)为广义坐标，各模态解耦的运动方程可归结为：

(6)

式中：ξr为模态r的阻尼比.

根据弹性反应谱理论，结构各阶振型的最大位移可根据最大加速度按下式计算：

(7)

值得注意的是各阶振型的最大值并非在同一时刻达到，因此需按下式确定张拉整体结构的最大动力响应：

(8)

式中：j为结果中所需用到的振型个数，通常情况下仅为第一阶振型.

1.2 二次线型最优控制理论

地震激励下结构体系的运动微分方程可描述为：

(9)

(10)

Y(t)=C0(t)X(t).

(11)

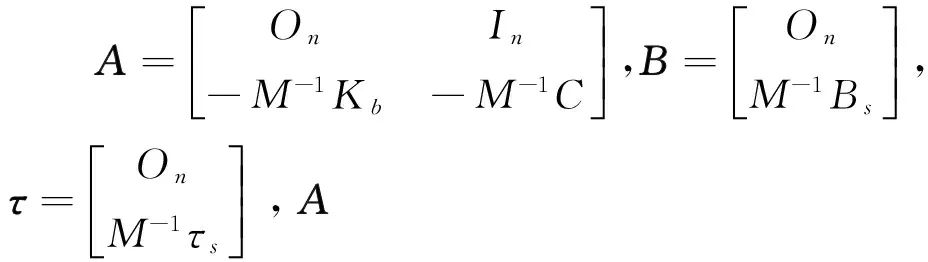
定义系统的二次型性能泛函为：

u(t)=VX(t).

(12)

式中：Q和R为由设计人员确定的权矩阵(均为对角矩阵)；t0和tf分别代表系统在初始状态和最终平衡态时对应的时间；V为与LQR控制器有关的增益矩阵.

利用优化控制理论求得二次型性能泛函的最优值如下：

.(13)

式中：G(t)为正定矩阵，可通过求解Riccati微分方程而得[13].

2 仿真模型建立

本节基于Wijdeven等[4]的工作，以一个8杆元30索元组成的平面张拉整体梁为研究对象，该梁底部两端为铰接，顶部两端为滑动连接(图1).采用改进的力密度法[14-15]确定结构各节点的初始坐标和各单元的预拉力(表1)，同时选取实测地震波EI Centro(1940)作为地震激励.

图1 平面张拉整体梁模型

表1 单元特性汇总

单元类型(单元编号)弹性模量/GPa长度/mm直径/mm横截面积/mm力密度/(kN·mm-1)预拉力/kN杆元(31～38)2102795.115017662.5-0.450-1257.8垂直索元(1;30)1701250.0401256.00.225281.3外侧斜交索元(3;4;27;28)1701952.6401256.00.225439.3外侧水平索元(2;5;26;29)1701500.0401256.00.525787.5内侧较短斜交索元(7;8;15;16;23;24)1701346.3401256.00.225302.9内侧较长斜交索元(11;12;19;20)1701600.8401256.00.225360.2内侧较短水平索元(6;9;14;17;22;25)170500.0401256.02.0251012.5内侧较长水平索元(10;13;18;21)1701000.0401256.02.0252025.0

利用LQR控制算法优化系统的控制力时，设计者需人为设定权矩阵Q和R[16]：

(14)

式中：α和β为由设计人员确定的权矩阵分配系数.本例中为了对比形变约束和作动力控制这两种情况，分别考虑如下三种控制方案：

(15)

表2列出了不同作动力加载位置和不同权矩阵情况下的控制方案.

表2 控制方案汇总

作动力加载位置连接作动器相关节点权矩阵所有单元(AM)所有节点1/2/3外侧杆元(OS)1,(2),5,6,11,12,15,(16)1/2/3内侧杆元(IS)3,4,9,10,7,8,13,141/2/3外侧斜交索元(OC)1,(2),3,4,13,14,15,(16)1/2/3内侧较短斜交索元(ISC)3,4,5,6,11,12,13,141/2/3内侧较长斜交索元(ILC)5,6,7,8,9,10,11,121/2/3

3 结果分析

3.1 权矩阵对振动控制的影响

如图2-图7所示，在作动器布置位置相同的前提下，不同的控制方案产生的体系动力响应行为是相似的.图中线条分别代表非控制方案、方案1(Q1/R1)、方案2(Q2/R2)、方案3(Q3/R3)的动力响应.由权矩阵的定义可知，相比于方案1，方案2更注重作动力控制；而相比于方案3，方案2更注重形变约束.正如预期，非控状态下，结构体系在地震激励下的位移响应是最大的.以图2为例，非控方案结构的位移响应大约在2.4 s时达到最大值569.69 mm，而此时其他三个控制方案对应的最大位移值分别为163.21 mm、50.30 mm和11.99 mm.最后两个方案的控制效果很接近，并且几乎完全消除了结构体系的变形，而第一个方案也明显减小了结构的位移响应.

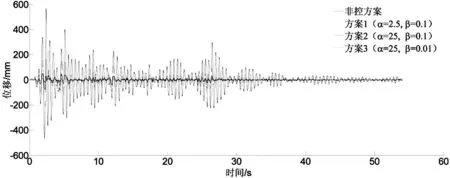
图2 所有单元均布置作动器的响应

图3 外侧杆元布置作动器的响应

图4 内侧杆元布置作动器的响应

图5 外侧索元布置作动器的响应

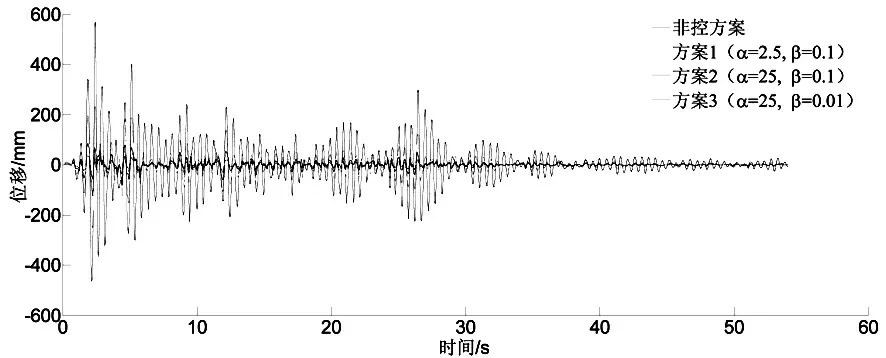
图6 内侧较短索元布置作动器的响应

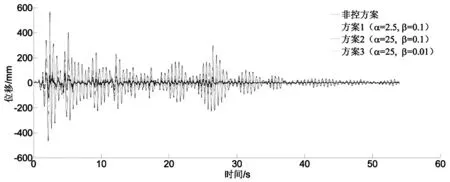
图7 内侧较长索元布置作动器的响应

3.2 作动器布置对振动控制的影响

实际上，除了权矩阵对振动控制会产生影响外，作动器的布置对振动控制也会产生不可忽略的影响.本文共研究了六组不同的作动器布置情况，除了在所有单元上均布置作动器这组情况外，其余五组情况均有四个单元被驱动.图8展示了三个控制方案在六组作动器布置情况下的最大位移响应值.总体而言，控制效果最好的是在所有单元上均布置作动器，使其最大程度地减小体系的最大位移响应值.但是，由于其消耗能量较大，大大增加了控制成本，使得控制性价比显著降低，因此这种布置方法是不实用的.这就使得关于研究作动器布置的有效性具有重大意义.以方案1为例，作动器布置位置离结构中心越近，位移响应峰值就越小，控制越有效.此外，将作动器布置在内侧杆元比布置在内侧索元上略有效.而这些结论对方案2却正好相反.对方案3而言，将作动器布置在外侧单元上比布置在内侧单元上更为有效.另外，与前两种方案类似的是，将作动器布置在外侧杆元上比布置在外侧索元上略有效.值得注意的是，在所有控制方案中，相比于将作动器布置在杆元或索元上而言，系统的动力响应似乎对作动器布置于外侧单元或内侧单元更为敏感.

3.3 作动力

从某种程度上讲，由于振动控制是昂贵的，因此分析各控制方案的不同作动器布置所需最大作动力是很有必要的(如图9).对比图8和图9的结果可知，方案1中六组不同的作动器布置所引起的结构位移响应之间有较大幅度的变化，但作动力之间却无明显变化，而方案2、方案3的表现却正好相反.

总体而言，最大作动力的表现形态和最大位移响应正好相反，即位移响应减少幅度越大，所需作动力的值就越大.而表现出这种相反的形态是合理的，这是因为系统的控制需求越大，所需的作动力当然就越大.值得注意的是，将作动器布置在所有单元是减少结构体系位移响应最为有效的方案，而从图9中可以看出，此方案所需最大作动力仍为最小.这个现象可以解释为，每个单元上所需的作动力相比于其他几种情况是最小的.实际上，由于在每个单元上都需布置作动器，其所需要的总作动力恰恰是最大的.

图8 各模拟方案的最大位移响应(最大位移/mm VS.作动器布置)

图9 各模拟方案的最大作动力(最大作动力/KN VS.作动器布置)

4 结论

张拉整体结构是由若干受压杆元和受拉索元组成的自适应结构体系，这类智能结构可以很容易地被操控并呈现出不同的形状.本文提出了使用主动控制技术理论来研究张拉整体的SRC问题，建立了地震激励下二维张拉整体梁的动力计算模型，分析讨论了影响控制结果的各类因素,得出以下结论：

(1)作动器布置则取决于形变约束和作动力控制两大因素.对方案2而言，将作动器布置在外侧单元上,尤其是杆元上，控制效果较佳；对于方案1、3，将作动器布置在内侧单元上，尤其是杆元上，控制效果较佳.

(2)相比增加形变约束的重要性，LQR控制器对增加作动力控制的重要性更为敏感.这也意味着，加强作动力的控制能够相对多的增加位移，但是反之减少相同的控制却减少不了相同的位移.至于具体应该选择哪种控制方案则取决于结构体系的需求.如果维持结构的原有形态是很重要的，那么方案2可以基本满足这个要求，保守起见，方案3是最好的选择.如果该结构中某些变形是可被接受的，则方案1应为性价比最高的方案.

(3)当设计方案对作动力的控制更为重视时，作动器布置应基于形变约束的原则，此时作动力的变化是可以忽略的.同样的，当设计方案对形变约束更为重视时，作动器的布置应基于作动力控制的原则.

参考文献：

[1]刘锡良，陈志华.一种新型空间结构-张拉整体体系[J].土木工程学报,1995,28(4):52-57.

[2]DJOUADI S, MOTRO R, PONS J C, et al. Active control of tensegrity systems [J].Journal of Aerospace Engineering,1998,11(2):37-44.

[3]KANCHANASARATOO N, WILLIAMSON D. Motion control of a tensegrity platform [J]. Communications in Information and Systems,2002,2(3):299-324.

[4]VAN D W J, DE J B. Shape change of tensegrity structures design and control [C]. USA:Proceedings of the American Control Conference.Institute of Electrical and Electronics Engineers Inc,2005:2522-2527.

[5]MASIC M, SKELTON R E. Selection of prestress for optimal dynamic/control performance of tensegrity structures [J]. International Journal of Solids and Structures, 2006,43(7):2110-2125.

[6]BEL H A N, SMITH I F C. Dynamic behavior and vibration control of a tensegrity structure [J]. International Journal of Solids and Structures,2010,47(9):1285-1296.

[7]GANESH R M, NARAYANAN S. Active control of tensegrity structures under random excitation [J]. Smart Material Structures,2007,16(3):809-817.

[8]GANESH R M, NARAYANAN S. Simultaneous optimization of structure and control of smart tensegrity structures [J]. Journal of Intelligent Material Systems & Structures,2009,20(1):109-117.

[9]张沛,冯健.张拉整体结构的稳定性判定及刚度分析[J].土木工程学报,2013,46(10):48-57.

[10]SADEGHI A, SADEGHI F. Seismic behavior of tensegrity barrel vaults [C].Valencia: Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium,2009:2263-2273.

[11]OHSAKI M, ZHANG J Y. Stability conditions of prestressed pin-jointed structures [J]. International Journal of Nonlinear Mechanics,2006,41(10):1109-1117.

[12]NISHIMURA Y. Static and dynamic analyses of tensegrity structures [J]. International Journal of Solids and Structures,2001,38(20):3615-3629.

[13]欧进萍.结构振动控制-主动、半主动、智能控制[M]. 北京:科学出版社,2003.

[14]FENG X D, GUO S H. A novel method of determining the sole configuration of tensgrity structures [J]. Mechanics Research Communications,2015(69):66-78.

[15]张志宏,张明山,董石麟.平衡矩阵理论的探讨及一索杆梁杂交空间结构的静力和稳定性分析[J].工程力学,2005,22(6):7-14,20.

[16]郭一峰,徐赵东,涂青,等.基于遗传算法的LQR算法中权矩阵的优化分析[J].振动与冲击,2010,29(11):217-220，264.