圆锥曲线最值问题的思考
2018-05-02曾月迪林嘉沁
曾月迪,林嘉沁
(莆田学院 数学与金融学院,福建 莆田 351100)
在数学师范生的培养中,中学数学方法论是重要的一门课,其针对数学思想方法,让学生的数学素养得到提升.在教学中,圆锥曲线是重要的一个内容.实际上,圆锥曲线不只是中学数学中的问题,而且其有较多应用,如文[1-3]等,所以我们从中学到大学都对圆锥曲线进行研究.而对于中学数学中圆锥曲线的探讨如文[4]等,其中圆锥曲线中最值问题的考察知识面广,综合性强,对学生知识储备要求高,因此常常作为中学考试和教师招考的热门题型,近几年有较多探讨如文[5]等.本文从一道高中数学联赛题的圆锥曲线最值问题出发,展开思考.
把2013福建高中数学竞赛题预赛12题第2小题[6]问题一般化为:如下图,

问题:已知A、B为抛物线:y2=2px(p>0)上的两个动点,点A在第一象限,点B在第四象限.l1、l2分别过点A、B且与抛物线相切,P 为 l1、l2的交点.设 C、D 为直线 l1、l2与直线 l:x=t(t>0)的交点,求△PCD面积的最小值.
1 从极端情况探讨问题
性质1 若交点P的横坐标是定值,则P点在x轴上,三角形PCD的面积取到最小值.
证明 设P坐标为 (x0,y0),x0<0,过点P的直线方程为y-y0=k(x-x0),并与抛物线y2=2px联立得:

若直线与抛物线只有一个交点即直线与抛物线相切,由(1)式得:Δ=0即

由此可知:若 k1,k2为(2)式的两个根,则.设两条相切直线与直线x=t(t>0)的交点为 C(t,y1)、D(t,y2).不妨设 y1>y2,则

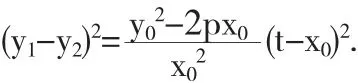
由此可知若x0,t固定时,当y0=0时,(y1-y2)2最小,即y1-y2最小,所以最小.
从而有:
定理1 设点P在直线x=x0<0上,则过点P与抛物线y2=2px(p>0)相切的直线,交直线 l:x=t(t>0)于 C、D 两点,所构成的三角形PCD的面积当P点在x轴上取最小值,且与抛物线的形状和直线 的位置无关.
性质2 若P点在x轴上,则原点到P点的距离与原点到l的距离的比值为1:3时,三角形PCD的面积最小,此时
证明 由性质1中的证明可知,若P点在x轴上,


注1 设过点P(x0,y0),x0<0与抛物线y2=2px(p>0)相切的直线,交直线l:x=t于C、D两点,所构成的三角形PCD的面积当P点在x轴上,原点到P点的距离与原点到l的距离的比值为1:3时取最小值,且与抛物线的形状无关.
2 从问题的正面解决探讨问题
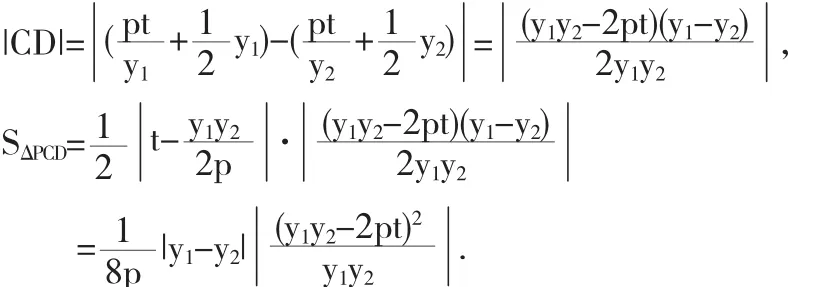
设 y1y2=-a2(a>0),|y1-y2|=m,由 (y1+y2)2=(y1-y2)2+4y1y2=m2-4a2≥0知,m≥2a,当且仅当y1+y2=0时等号成立.
注2 此时,说明当P的横坐标固定时,y1+y2=0,m=2a时,SΔPCD最小.那么P的纵坐标为0,即P点在x轴上,SΔPCD最小,这就是上述极端情况中性质1.

例 (2013福建高中数学竞赛题):已知A、B为抛物线C:y2=4x上的两个动点,点A在第一象限,点B在第四象限.l1、l2分别过点 A、B 且与抛物线 C 相切,P 为 l1、l2的交点.设C、D为直线l1、l2与直线l:x=4的交点,求△PCD面积的最小值.
解 由上面两种方法可知:

注2 极端原理是关键的数学思想与方法,在师范生数学方法论的教学中,极端原理是关键的一部分内容.极端原理在数学问题研究中,对于存在性是经常讨论的,并与抽屉原理一般相互应用,有较多的研究如文[7]等.而在解决本文中的问题时,两种方法难度系数差不多.第一种方法,具体找出了最值存在的情形.如果利用第二种方法,并没有去探讨的坐标 (其实就是极端情况),直接求解也是能解决问题的.但是这样就不能找出本质的问题,同时也发现不了问题的实质.
定理2 已知A、B为抛物线:y2=2px(p>0)上的两个动点,点A在第一象限,点B在第四象限.l1、l2分别过点A、B且与抛物线相切,P 为 l1、l2的交点.设 C、D 为直线 l1、l2与直线l:x=t(t>0)的交点,则所构成的三角形PCD的面积当点A、B关于x轴对称,即P点在x轴上,原点到P点的距离与原点到l的距离的比值为1:3时,△PCD面积取最小值,且与抛物线的形状无关.
参考文献:
〔1〕Liu Y,Xu C.Approximation ofconic section by quartic Bézier curve with endpoints continuity condition[J].Applied Mathematics-A Journal of Chinese Universities,2017,32(1):1-13.
〔2〕Han X,Guo X.Optimal parameter values for approximating conic sections by the quartic Bézier curves[J].JournalofComputationaland Applied Mathematics,2017,322:86-95.
〔3〕赵欢,喜丘夏.可重建圆锥样条曲线的带多参数三点细分法[J].系统仿真学报,2017,29(11):2624-2628.
〔4〕崔禹.巧用差分法解决圆锥曲线弦的中点问题[J].数学学习与研究,2017(21):125-126.
〔5〕韩文美.圆锥曲线中最值问题的求解策略[J].中学生数理化(高二数学),2017(1):32-33.
〔6〕陈德燕.2013年全国高中数学联赛福建赛区预赛[J].中等数学,2014(03):29-34.
〔7〕赵泽福.竞赛数学中“存在性”问题的一种解法[J].赤峰学院学报(自然科学版),2015,31(8):7-9.
