桥墩直径及高度对桥梁地震响应影响分析
2018-05-02廖瑾,桂睿
廖 瑾,桂 睿
(1.中国公路工程咨询集团有限公司,北京市 100089;2.北京市市政工程设计研究总院有限公司,北京市 100082)
0 引言
北京地区是我国地震活动较强烈的地区之一,经济发达,交通繁忙。而公路桥梁是生命线系统工程的重要组成部分,一旦生命线工程遭到地震破坏,将会带来极大经济损失及社会影响。大量地震灾害调查结果表明,水平地震作用往往是最主要的地震作用,因此墩柱高度、强度等特性是桥梁抗震特性的重要因素[1]。
桥梁墩柱高度及刚度对于桥梁自振频率影响较大,与房屋等民用建筑不同,双柱式桥墩桥梁自振周期通常较大,大于0.1s,因此墩柱高度越高,刚度越小,桥梁自振周期越大,地震水平设计加速度反应谱值越小,墩柱水平剪力越小。但墩柱越高,同一剪力产生墩底弯矩越大,墩顶水平位移越大。墩柱高度对于桥梁抗震性能影响较为复杂。因此桥梁设计中重点分析桥墩高度对于桥梁抗震的影响很有必要。
本文以北京兴延高速公路白羊城沟特大桥双柱式墩柱连续梁桥为背景,分析桥墩高度及直径等因素对桥梁结构抗震性能的影响,指导设计过程中对墩柱刚度的合理优化。
1 工程概况
白羊城沟特大桥位于北京昌平区北部山区,周边为低山丘陵地貌。桥梁上部结构采用3×30m或4×30m预应力混凝土连续小箱梁。下部结构采用双柱墩,柱径为1.6~2m,墩柱高度约5~35m。该桥桥区沿线地质以卵石土为主。计算时按B类桥梁考虑。
根据该项目地震安评报告,该桥场地特征周期Tg为0.4s,场地类别为Ⅱ类,设防烈度为8度,地震动峰值加速度为0.2g。有限元模型见图1。
图1 有限元模型(16m墩高)
2 地震响应分析模型
本文以三跨连续梁桥为背景进行抗震分析和研究。
2.1 模型建立
上部结构为预应力混凝土小箱梁,单幅断面为4片主梁,各片主梁之间采用虚拟桥面板单元连接建立梁格单元。支座采用弹簧模拟普通板式橡胶支座,支座参数根据规范进行计算。
下部结构采用双柱式桥墩。E1计算时下部结构采用弹性单元模拟,墩柱抗弯刚度按毛截面计算。E2计算时,考虑墩柱可能产生塑性变形,对墩柱刚度进行折减。
桩土作用采用土弹簧模拟,桩直径D=1.8m,桩长为18m,按摩擦桩计算,桩底土为卵石层,10m范围表层土m值按30000考虑,根据规范6.3.8,计算土弹簧时m动=2m静=60000kN/m4。底层土m值按100000考虑,计算土弹簧时m动=2m静=200000kN/m4。,桩底约束采用一般支承模拟。
根据空间杆系理论,采用Midas/Civil2012进行计算分析,对结构模型进行水平加速度反应谱分析计算,模态组合采用CQC法。
2.2 地震参数
本桥E1、E2作用均采用多振型反应谱法,水平设计加速度反应谱S由规范5.2.1确定。水平设计加速度反应谱参数见表1。
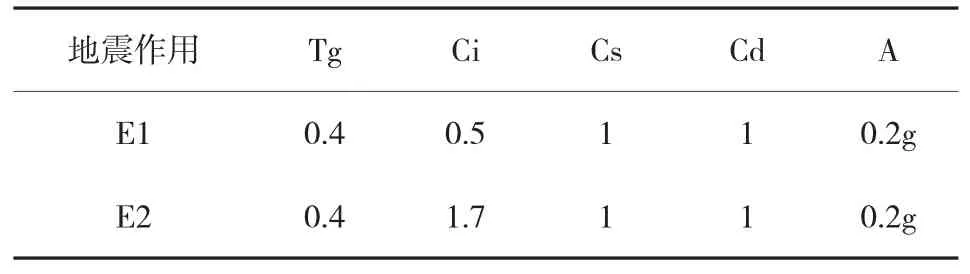
表1 反应谱参数
3 计算分析
3.1 墩柱直径对抗震性能的影响
分别采用1.6m,1.8m,2m直径墩柱建立有限元模型,分析不同直径墩柱对于桥梁抗震性能的影响。墩高采用本桥梁平均墩高16m。E1地震工况下计算结果见图2~图4。
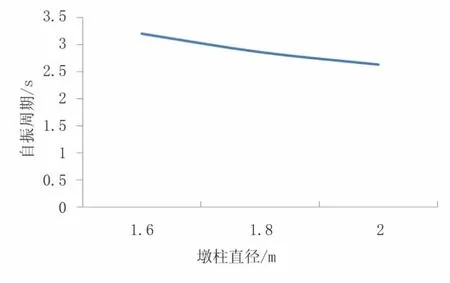
图2 基频
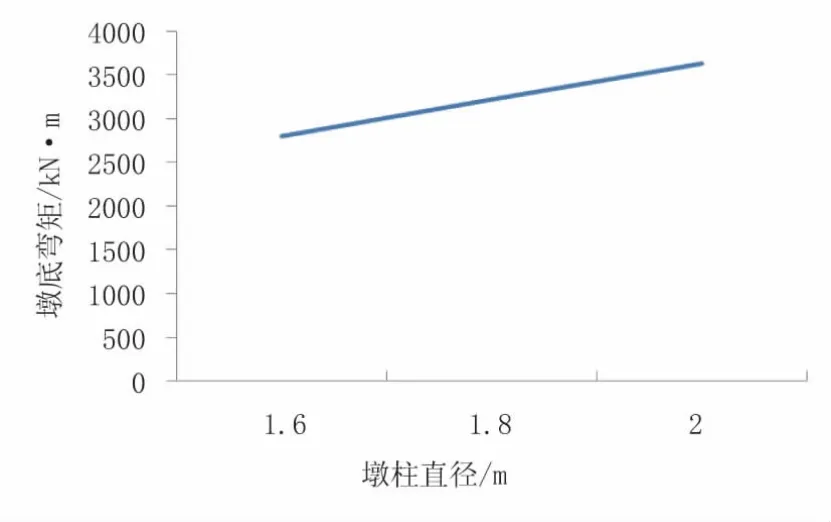
图3 墩底弯矩
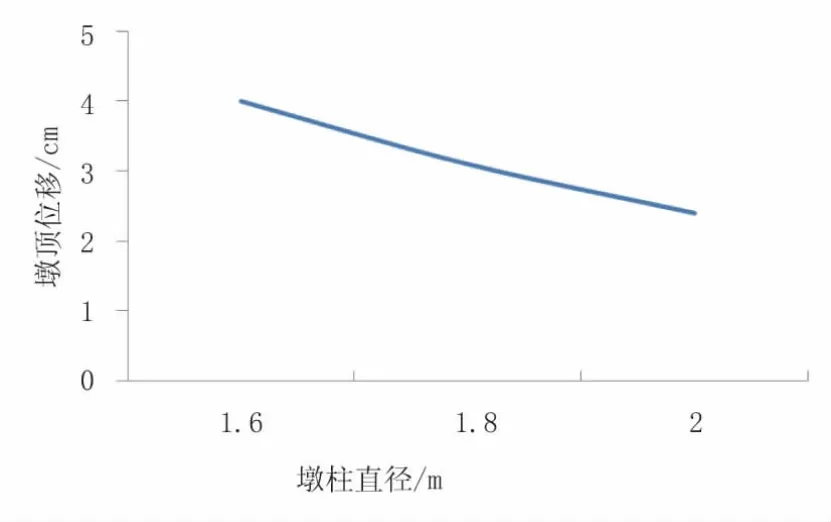
图4 墩顶位移
由图2~图4可知,桥梁自振周期随墩柱直径变化明显,墩顶位移随墩柱直径增大而减小。但墩柱直径越大,结构刚度增大,自振周期越小,墩底弯矩随墩柱直径增大而增大,因此设计时应具体情况具体分析,避免墩柱直径过大对结构抗震性能产生不利影响。
结构体系抗震能力综合表现为强度、刚度及变形能力。根据本桥计算结果,墩柱高度为16m,墩柱直径为1.6m及1.8m时,墩顶容许最大变形值分别为0.226m及0.18m。因此当墩柱直径过大时,墩柱变形能力减小,不利于结构体系整体抗震能力。
当墩柱直径过大时,有违结构体系强剪弱弯的抗震设计理念。墩柱抗弯刚度过大,会转移塑性铰产生位置,不利于结构稳定[2]。
3.2 墩柱高度对地震作用下墩底弯矩的影响
根据全桥桥墩高度范围,选取8m、16m、27m三种墩柱高度分别建立模型,分析不同高度墩柱内力弯矩响应。计算结果见图5~图7。

图5 基频
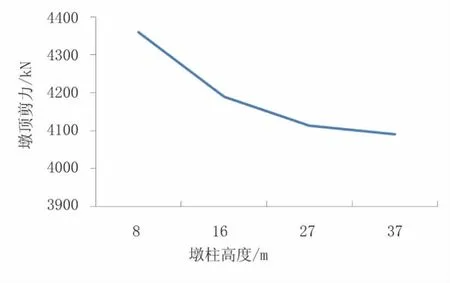
图6 墩顶剪力
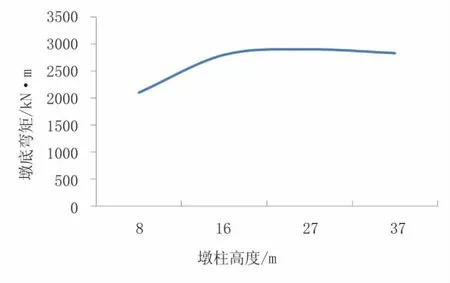
图7 墩底弯矩
由图5~图7可知,桥梁自振周期随墩柱高度变化明显,墩柱越高,自振周期越大。自振周期均大于特征周期0.4s,因此根据规范计算公式,随墩柱高度增加,水平设计加速度反应谱相应减小,墩顶剪力随墩柱高度增加相应减小,有限元计算结果与预期相符。墩底弯矩与墩柱高度变化为非线性关系,当墩柱小于16m时,墩底弯矩随墩柱高度增加而增大;当墩柱高度大于16m时,墩底弯矩变化不明显。因此当墩柱高度大于16m小于37m时,可不增加墩柱直径及配筋,但仍需对墩柱延性进行验算。
3.3 E2地震下墩柱位移验算方法
本文以1.6m直径墩柱为例,对墩柱延性验算方法进行分析。墩柱截面钢筋取45Φ28,墩柱混凝土采用C40。恒载下墩底轴力5500kN。
(1)墩柱弯矩曲率曲线计算
本桥墩柱截面屈服曲率由MIDAS有限元软件计算,求得墩柱截面初始屈服弯矩7666kN·m,初始屈服曲率0.00204。屈服弯矩(理想化)10331kN·m,屈服曲率(理想化):0.00275。极限弯矩10442kN·m,极限曲率0.0466。
(2)墩柱位移验算
在E1地震下,墩柱在弹性范围内工作,验算的是结构的强度,因此采用偏于安全的墩柱毛截面特性进行抗震分析;而E2地震作用下,结构允许进入弹塑性工作状态,采用毛截面进行计算出的墩柱变形偏小,不利于结构安全,因此需采用开裂后的等效截面进行验算[3]。由公式(B.0.1-2),墩柱截面屈服曲率Φy为:
本桥墩柱截面屈服曲率由MIDAS有限元软件计算,根据墩柱配筋进行M-Φ分析。计算结果见表2。
(3)墩柱容许位移计算
E2地震作用下,按下式验算墩顶位移:
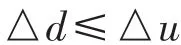
式中:△d为E2地震作用下墩顶位移;△u为桥墩容许位移。
E2地震作用下,墩顶顺桥向和横桥向水平位移按抗震规范计算,△d=Cδ。场地特征周期Tg=0.4s,顺桥向结构自振周期T=3.1s≥Tg,取C=1。
墩柱顺桥向容许位移按《公路桥梁抗震设计细则》计算,见表3。
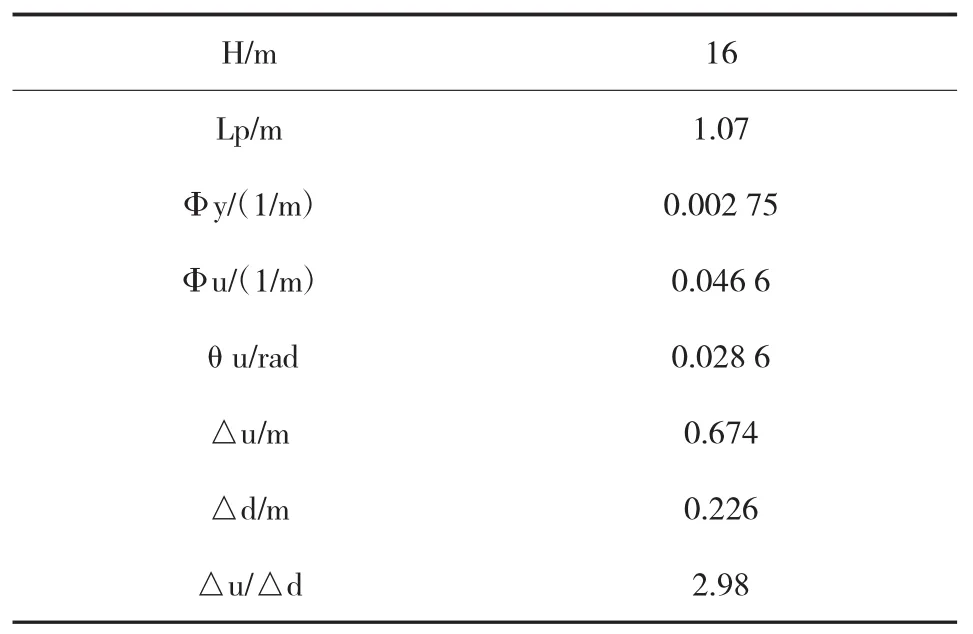
表3 E2墩柱顺桥向位移验算表
4 结语
(1)在地震作用下,随着墩柱直径增加,墩顶位移减小,但墩底弯矩相应增加。因此不宜盲目增加墩柱直径。设计时应符合强剪弱弯的设计理念,增强结构延性变形能力,避免结构剪切破坏等脆性破坏。
(2)在桥墩截面尺寸不变时,随着墩柱高度增加,墩底弯矩前期相应增加。当墩柱达到一定高度后,墩底弯矩变化较小。因此当墩柱超过一定值时,墩柱抗弯强度往往能满足要求,而墩顶位移将对桥梁抗震性能产生较大影响。
参考文献:
[1]范立础.桥梁抗震[M].上海:同济大学出版社,1997.
[2]范立础,卓卫东.桥梁延性抗震设计[M].上海:人民交通出版社,2001.
[3]JTG/TB02-01-2008,公路桥梁抗震设计细则[S].
