车载充电机的无模型功率控制研究

陈乾辉,吴德刚

(商丘工学院 机械工程学院，河南 商丘 476000)

电动汽车电池技术已经成为衡量电动汽车品质的核心技术之一，作为连接电池系统与电网的接口，电池充电器是实现电池高效、快速充电的核心[1].目前，最常见的两种电池充电器是车载充电机和充电桩[2].车载充电机一般采用功率因数校正(Power factor correction，PFC) AC/DC变换器和全桥DC/DC变换器级联的结构形式，前端PFC AC/DC变换器不仅能将电网的AC转换为DC，还可以实现PFC，后端则可实现电池系统的智能充电[3,4].然而，由于PFC AC/DC变换器的性能直接影响充电机接入电网后电能的质量(比如多次谐波使电网电压畸变，设备损坏等)、电池组的充电效率、电池的寿命等[5,6]，因此，如何实现PFC AC/DC变换器的高性能控制，成为我们亟待解决的难题.

目前，PFC AC/DC变换器的控制策略主要有平均电流控制、非线性控制、基于微分平坦控制的PFC AC/DC变换器功率控制方法、无模型控制(Model-free control，MFC)方法等[7,8].在采用这些控制方法的过程中，存在抗干扰能力弱、动态特性差、模型的不确定性、未知扰动的动、静态性能的鲁棒性，针对上述控制方法存在的缺陷，提出了车载充电机PFC AC/DC 变换器的无模型功率控制(Model-free power control，MFPC)，该方法根据PFC AC/DC变换器的输入、输出(I/O)建立超局部模型(Super-partial Model，SPM)，进而设计相应控制器，该控制器控制结构简单，且对系统内外干扰、测量噪声、模型动态等有很强的鲁棒性.

1 无模型控制

将一单输入单输出(Single input single output，SISO)非线性系统的数学模型用SPM表示为

y(v)=F+αu,

(1)

其中，y——系统输出变量；y(v)——y的v阶微分值；v——大于等于1的整数，一般选1或2；u——系统输入变量；F——SPM中的未知部分，包括未知参数和内外部干扰；α——不具备物理意义的常数，保证αu和yv的幅值在同一数量级.

取v=1，由式(1)可得SISO系统的SPM，即

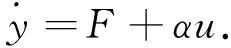
(2)

基于SPM的无模型控制器可表示为

(3)

(4)

由式(3)和(4)可知，MFC系统可表示为

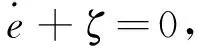
(5)

其中,e=y*-y.由式(5)可知，ζ选择越恰当，系统输出越稳定.

若ζ选用比例控制，则无模型控制器可表示为

(6)

其中,Kp——比例系数.

由于未知部分的准确性决定系统的控制精度，当时间很小时，F近似为常数，因此，式(2)可近似为

(7)

其中,θ——分段常函数.

对式(7)做拉普拉斯变换，可得：

(8)

其中,y0——y在采样区间的初始值.

对等式(8)两侧求s的微分，可得：

(9)

为了滤除噪声，需在等式(9)两侧同乘s-2，可得：

(10)

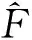
(11)

其中,Ts——采样频率；nF——窗口序列长度；[0，nFTs]——非常短的滑动的时间窗口.

特别注意，u[0]，u[1]，…，u[nF]和y[0]，y[1]，…，y[nF]分别为系统I/O的采样值.

nF和α选择越恰当，F的预估越准确，无模型控制器的控制能力越强.若输出参考值含有噪声，则输出参考值的微分可通过式(12)获取.

(12)

2 PFC AC/DC 变换器的MFPC

根据PFC AC/DC 变换器的工作原理，选择恰当的I/O，根据I/O构建PFC AC/DC 变换器的SPM，并在PFC AC/DC 变换器的SPM基础上，设计无模型电流-功率控制器，实现PFC AC/DC 变换器MFPC.

车载充电机前端PFC AC/DC 变换器的状态方程为

(13)

该系统的平坦输出为输入功率pin与占空比d的关系为

(14)

其中，

为实现变换器的MFPC，以pin为系统输出，d为系统输入，由式(2)可得PFC AC/DC 变换器的SPM，即

(15)

由式(14)可知，SPM的未知部分包含 中的各种内外部干扰，为实现系统控制的精确性，α与B的取值应相似.

由PFC AC/DC 变换器SPM获得无模型电流-功率控制器，即

(16)

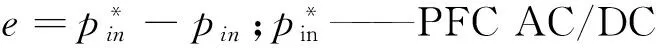
(17)

(18)

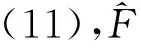
(19)

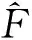
为实现对系统状态的准确估计，α应时刻随系统变化，即

α=c|vin|Vo,

(20)

其中,c是与电感值L相关的常数.

3 系统建模与仿真

根据上述车载充电机前端PFC AC/DC 变换器的控制器的设计，建立MFPC的PFC AC/DC 变换器的仿真模型，以电阻模拟车载充电机的恒流充电过程，仿真模型如图1所示.

图1 MFPC的PFC AC/DC 变换器的仿真模型

3.1 α仿真验证

给定控制器参数：nD=15，nF=15，Kp=le5，若α为变值，c=1e-4，若α为恒值，c=1e-9.α在恒值和式(20)所描述系统变值两种情况下，验证系统的控制能力.

给定参数：vin(rms)=220 V,P0=2 KW.

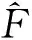
图2 恒α时

图3 恒α时和pin

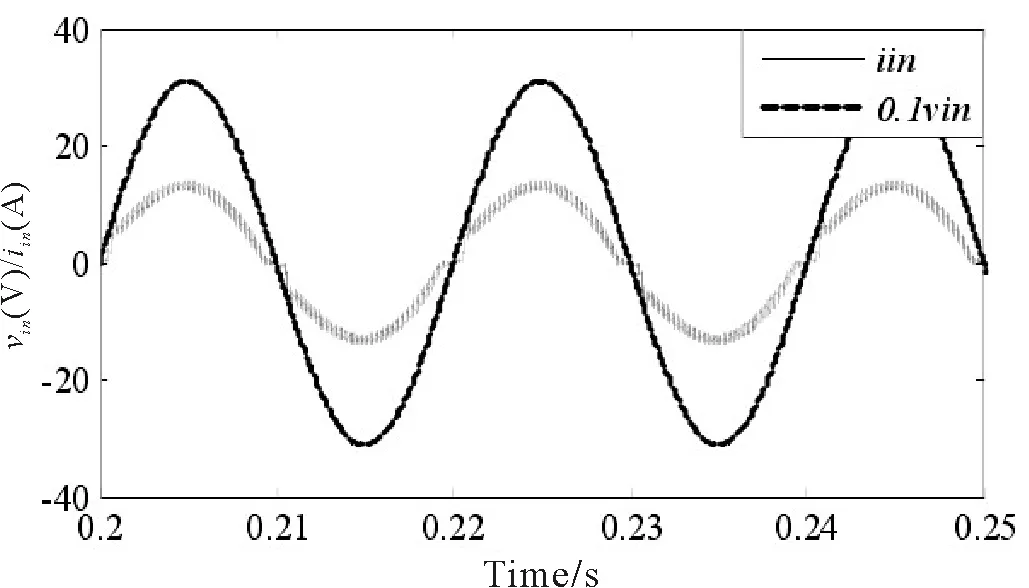
图4 恒α时vin和iin

图5 恒α时V0

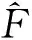
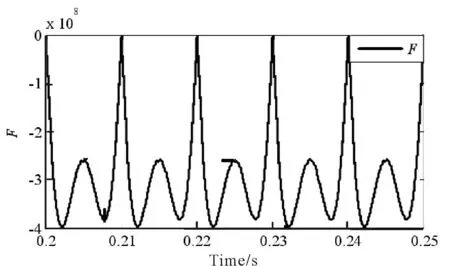
图6 变α时

图7 变α时和pin

图8 变α时vin和iin

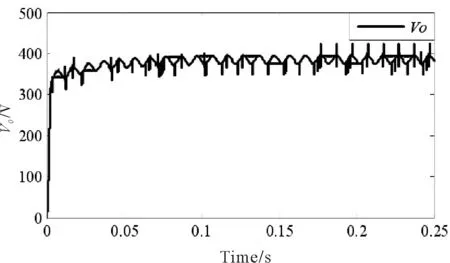
图9 恒α时V0

3.2 抗干扰实验、仿真验证

给定参数：vin(rms)=220 V，P0=1.7 KW，负载0.2 s后突变到2 KW.

MFPC的车载充电机 PFC AC/DC 变换器的iin如图10所示，V0如图11所示.仿真结果表明：MFPC的PFC AC/DC 变换器的iin在负载突增时，能瞬时到达新稳态；V0从327 V经过短时电容恒流充电平稳到达385 V.

给定参数：vin(rms)=220 V，P0=2 KW，测试电容由990 μF降到660 μF.

MFPC的车载充电机 PFC AC/DC 变换器的V0如图12所示.测试电容变化时，MFPC的变压器V0在0.035 s后到达新稳态，具有很强的鲁棒性.

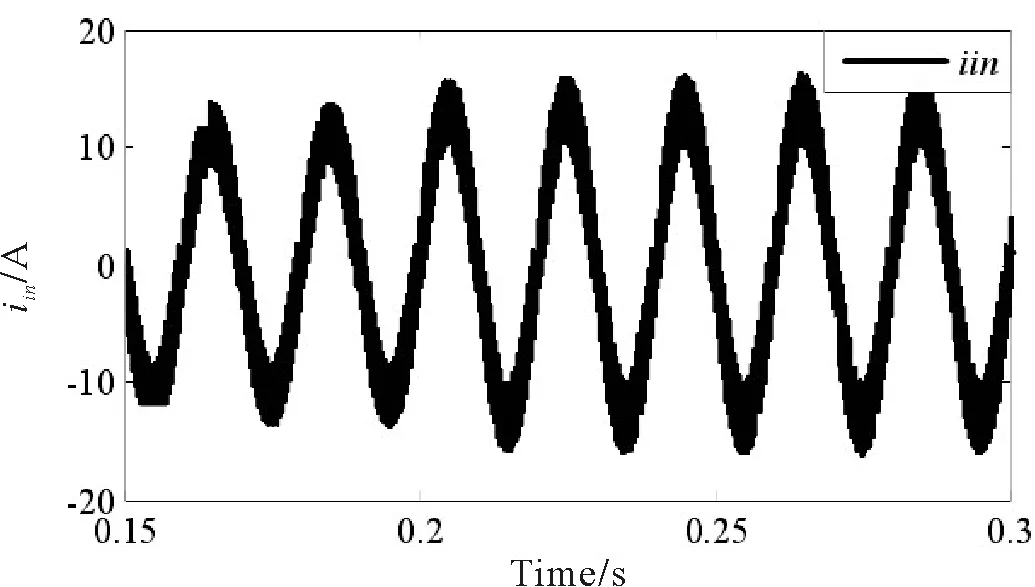
图10 负载突变时MFPC下的iin

图11 负载突变时MFPC下的V0

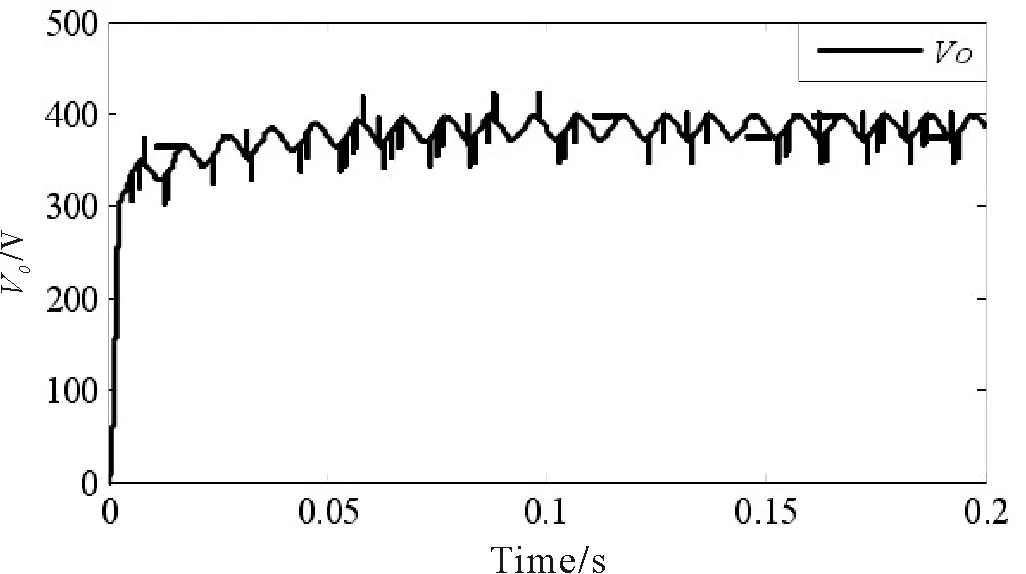
图12 测试参数变化时MFPC下的V0

4 结语

针对常用PFC AC/DC变换器控制存在的缺陷，提出了车载充电机 PFC AC/DC变换器的MFPC研究，实验、仿真结果表明，该方法不仅结构简单，且在变α下MFPC的PFC AC/DC 变换器的电流谐波失真值仅为1.21%，参数变化时，V0在0.035 s左右的时间可以从327 V平稳到达385 V，具有更好的动态性、更高的功率因数和更强的鲁棒性，完全满足对新能源汽车低碳减排的需要.

参考文献：

[1] 刘红丽，马正来，聂 鹏.4KW电动汽车车载充电机的研究与实现[J].电气传动，2017,47(2)：20-13.

[2] Musavi F，Craciun M,Gautam D S,et al.An LLC Resonant DC-DC Converter for Wide Output Voltage Battery Charging Applications[J].IEEE Trans.Power ELectron， 2013, 28(12):5 437-5 445.

[3] 曹灵灵.车载充电机 PFC AC/DC变换器的高性能控制[D].合肥：合肥工业大学，2017.

[4] 郭晓丹，李晓辉，李 磊，等.300KW非车载充电机现场检定系统的设计[J].电测与仪表，2017,54(8)：123-128.

[5] 黄菊花，何剑平，曹 铭.电动汽车电池管理系统抗工频磁场设计[J].电测与仪表，2016,42(7)：80-82.

[6] 胡 勇.电动汽车交流充电桩控制装置的研究与设计[D].绵阳：西南科技大学，2017.

[7] 杜常清，潘志强，赵奕凡，等.电动汽车车载充电系统研究[J].电源技术，2016，40(6)：1 277-1 279.

[8] 陈小虎，陈息坤.新型混合动力电动汽车车载充电机的研究[J].电气自动化，2015,37(6)：21-25.