液力惯容器特性研究

王 乐， 毛 明， 雷强顺， 陈轶杰， 张 旭

(中国北方车辆研究所，北京 100072)

从惯容器概念提出至今已出现多种结构形式,其结构分类如图1所示[1]。齿轮齿条式惯容器是最早被开发的惯容器样机，采用齿轮齿条运动副作为传力机构，通过将齿轮齿条之间的相对直线运动转化为飞轮的转动，实现对飞轮惯性的封装[2]。滚珠丝杠式惯容器是采用滚珠丝杠运动副作为传力机构，滚珠丝杠运动副包括滚珠丝杠和滚珠丝杠螺母，两者均可作为主动件或从动件，滚珠丝杠和飞轮固结作为从动件一起被驱动旋转时，称之为丝杠旋转式滚珠丝杠惯容器[3]，滚珠丝杠螺母和飞轮作为从动件被驱动作旋转运动时，称之为螺母旋转式滚珠丝杠惯容器[4]。扭转式惯容器的传动机构为具有一定扭转传递效率的扭转机械结构，惯性装置为飞轮。已开发的扭转式惯容器有少齿差行星齿轮扭转式惯容器和摆线钢球扭转式惯容器[5]。液压泵式惯容器是以液压活塞带动液压泵的叶轮轴旋转作为传动机构，利用活塞杆和液压缸之间的压力差使液压马达旋转，从而驱动飞轮旋转，实现对飞轮惯性的封装[6]。液压活塞式惯容器通过活塞移动形成液压，带动另一个活塞运动来作为传动机构，在此过程中利用两活塞横截面积的差异实现惯性的封装。已开发的液压活塞式惯容器有分体式和一体式两种[7]。本文对液力惯容器进行研究，考虑流体摩擦、沿程压力损失、进出口压力损失等情况。

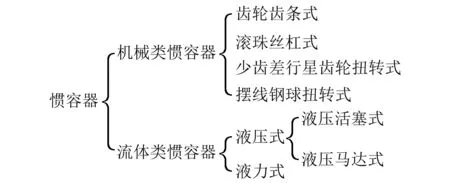
图1 惯容器分类 Fig.1 The classification of inerters

液力惯容器是一种利用具有一定质量的液体在细长管中的流动产生惯性的装置[8]。根据螺旋管的布置形式不同，液力惯容器可以分为外置螺旋管式和内置螺旋管式两种，分别如图2和图3所示。

图2 外置螺旋管式液力惯容器原理简图 Fig.2 Schematic of hydraulic inerter with ex-helical tube

图3 内置螺旋管式液力惯容器原理简图 Fig.3 Schematic of hydraulic inerter with in-helical tube

本文以外置螺旋管式液力惯容器为研究对象，其结构简图如图4所示，主要包括端点A、左腔、活塞、螺旋细长管、右腔、油缸、行程室和端点B。压缩行程和拉伸行程中，左腔和右腔的活塞实际工作面积相等，缸内液体体积维持定值，惯容器在这两个行程中的工作原理相同。以拉伸行程为例，端点A与活塞固结，端点B与油缸固结，当端点A相对于端点B向左运动时，由于液体不可压缩，左腔液体在活塞的推动下经螺旋细长管从左腔流入右腔，通过液体在螺旋细长管中的流动，来实现对液体流动惯性的封装[9-10]。

1-端点A;2-左腔;3-活塞;4-螺旋细长管;5-右腔;6-油缸;7-行程室;8-端点B图4 外置螺旋管式液力惯容器结构简图 Fig.4 Structure of hydraulic inerter with ex-helical tube

1 液力惯容器特性的数学建模

1.1 假设

为便于分析液力惯容器装置的主要性能，建立数学模型时，作以下假设：

(1)液体在流动过程中，不存在泄漏，故系统满足体积守恒；

(2)液体连续且不可压缩，密度保持不变；

(3)不考虑势能、热能散失及温度变化对液体特性的影响。

1.2 数学模型

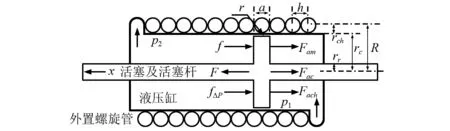
图5 外置螺旋式液力惯容器受力分析图 Fig.5 Force analysis of hydraulic inerter with ex-helical tube

以拉伸行程为例，对活塞进行受力分析，如图5所示。令从右向左方向为正，根据牛顿第二定律，有如下平衡关系：

F-f-fΔp=Fam+Fac+Fach

(1)

式中：F为活塞受到的轴向外力；单位N；f为活塞与油缸内壁的摩擦力，单位N；fΔp为液体流动过程中的阻尼力，单位：N；Fam为活塞运动形成的惯性力，单位N；Fac为油缸内液体流动形成的惯性力，单位N；Fach为螺旋管内液体流动形成的惯性力，单位N。

液体在油缸和螺旋管内流动时，与缸壁和管壁之间产生黏滞摩擦，为系统带来压降损失。此过程中，液体流动受到的阻尼力：

fΔp=(p2-p1)Ap

(2)

式中：p2为油缸左腔压力，单位Pa；p1为油缸右腔压力，单位Pa；Ap为活塞实际工作面积，其近似为油缸截面积Ac减去活塞杆截面积Ar，三者单位均为m2。

螺旋细长管进、出口及螺旋管内壁的压力损失，具有如下关系：

p2-p1=Δpi+Δpch+Δpo

(3)

式中：Δpi为螺旋细长管进口处的压力损失，单位Pa；Δpch为螺旋细长管中液体黏性造成的压力损失，单位Pa；Δpo为螺旋细长管出口处的压力损失，单位Pa。

式(1)可整理得：

F=f+ΔpchAp+ΔpiAp+ΔpoAp+Fam+Fac+Fach

(4)

分析式(4)中各项的物理意义，ΔpchAp为螺旋细长管沿程压力损失引起的阻尼力，记为fch，单位N；ΔpiAp为螺旋管进口压力损失引起的阻尼力，记为fi，单位N；ΔpoAp为螺旋管出口压力损失引起的阻尼力，记为fo，单位N。

为方便计算和理解，将活塞所受摩擦力、阻尼力之和记为Fd，单位N；将所有惯性力之和记为Fa，单位N。对式(4)整理可得：

F=Fd+Fa

(5)

其中：

(6)

1.3 摩擦力、阻尼力分析

(1)液体在螺旋管中流动产生阻尼力fch

根据Rodman和Trenc在2002年的研究成果，液体在螺旋细长管中的压力损失可近似估计：

(7)

式中：fF为范宁摩擦因数，无量纲；u为螺旋管中液体的平均流速，单位m/s；Re为雷诺数，无量纲；lch为螺旋细长管的长度，单位m；Dh为水力直径，单位m；μ为液体运动黏度系数，单位PaS。

根据液体体积守恒有：

(8)

其中：

(9)

(10)

式(9)和式(10)中，rc为油缸内半径，单位m；rr为活塞杆半径，单位m；rch为螺旋管内侧半径，单位m。Ach为细长螺旋管横截面积，单位m2。

整理式(8)可得：

(11)

液体在弯管中流动时在离心力作用下会产生二次流现象，二次流现象受液体流动时的惯性、液体黏度和弯管的曲率半径等影响，其特征参数为狄恩数De(Dean number)，有公式[8]：

(12)

根据Rodman和Trenc在2002年的研究成果，式(7)中的范宁摩擦因数fF与雷诺数Re的乘积fFRe是狄恩数De的函数，该函数关系可简化为线性关系，有公式[8]：

fFRe=0.034De+17.59

(13)

因此，液体流经螺旋管时的压降损失：

(14)

将式(14)改写为：

(15)

式中：

(16)

(2)螺旋管进、出口阻尼力fi和fo

螺旋管进出口处的压力损失是由于液体在油缸与螺旋细长管连接处流速急剧变化引起，有经验公式[11]：

(17)

(18)

将式(17)和(18)分别与式(15)的第一项进行比较，得：

(19)

(20)

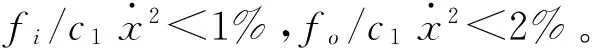
(3)活塞与油缸内壁的摩擦力f

活塞与油缸内壁间的摩擦力为剪切摩擦，可近似表示为[12]：

(21)

显然有：Af=2πrpa

(22)

式中：rp为活塞的半径，单位m；a为活塞高度，单位m。

此时式(21)可整理得：

(23)

将式(23)与式(15)的第二项进行比较，得：

(24)

1.4 惯性力

(1)螺旋管中液体流动产生的惯性力

记螺旋管中流动液体的总质量为mhel，单位kg，则有：

mhel=ρlchAch

(25)

活塞及活塞运动为直线运动，其运动以位移计量。则螺旋管中液体的运动为绕活塞(或油缸)轴线做圆周运动，其运动以弧度计量。根据体积守恒，则有：

(26)

式中：θ为液体在螺旋管中流动的角位移，单位rad。整理得：

(27)

螺旋管中液体流动的转动惯量近似为：

J=mhelR2

(28)

式中：J螺旋管液体流动的转动惯量，单位kg·m2。

同时惯容器储存的惯性能量为：

(29)

结合式(28)和式(29)，可得：

(30)

通常情况下，[h/(2πR)]2远小于1。因此，分析外置螺旋管式液力惯容器的惯质系数b时，可近似有下式：

(31)

由式(31)可知，外置螺旋管式液力惯容器的惯性力与螺旋管中流动液体质量之比近似于活塞实际工作面积与螺旋管道横截面积之比的平方。通常情况下，活塞实际工作面积较螺旋管横截面积大得多，因此，外置螺旋管式液力惯容器的惯质系数很大。

经推导螺旋管中液体流动产生的惯性力为：

(32)

(2)油缸内液体流动产生的惯性力

记油缸中流动液体的总质量为mcyl，单位kg，则有：

mcyl=ρAplc

(33)

式中：lc为油缸的有效长度，单位m。

lc=l-a

(34)

式中：l为油缸的总长度，单位m。

油缸内液体流动形成的惯性力为：

(35)

将式(35)与式(32)进行比较得：

(36)

由于螺旋管横截面半径rch远小于螺旋管的曲率半径R，通常情况下，有Fac/Fach≪1%。因此，油缸内液体流动产生的惯性力可以忽略不计。

(3)活塞运动产生的惯性力

活塞运动形成的惯性力为：

(37)

式中：mpis为活塞及活塞杆的质量，单位kg。

将式(37)与式(32)进行比较得：

(38)

由于螺旋管横截面积Ach远小于活塞实际工作面积Ap，通常情况下，有Fam/Fach≪1%。因此，油缸活塞运动产生的惯性力也可以忽略不计。

1.5 等效模型

拉伸行程中，螺旋管式液力惯容器的合力F：

(39)

对压缩行程进行分析，阻尼力的方向与速度方向相反，有：

(40)

综合式(39)和式(40)可得外置螺旋管式液力惯容器的数学模型：

(41)

式中：c1、c2、b分别由式(16)、(31)计算，它们均只与液力惯容器的结构和液体参数有关。

式(41)中，前两项为非线性阻尼环节，第三项为理想惯性环节。因此，外置螺旋管式液力惯容器可等效为非线性阻尼与理想惯容器的并联结构，其等效模型如图6所示。

图6 外置螺旋管式液力惯容器等效模型 Fig.6 eq-model of hydraulic inerter with ex-helical tube

2 液力惯容器特性的试验研究

通过调研发现国内还没有出现任何一款液力惯容器，很多学者只是停留在理论研究阶段。为了更好的研究液力惯容器的特性，运用三维设计软件PRO/E，作者设计研制了一款外置螺旋管式液力惯容器，其三维结构图和二维图分别如图7、图8所示，这是目前我国第一个外置螺旋管式液力惯容器样机。

1-铰链A;2-活塞及活塞杆;3-端盖A;4-端盖B;5-铰链B;6-传力筒;7-螺旋管;8-缸筒;9-接头总成图7 外置螺旋管式液力惯容器三维结构、实物图 Fig.7 3D and sample diagrams of hydraulic inerter with ex-helical tube

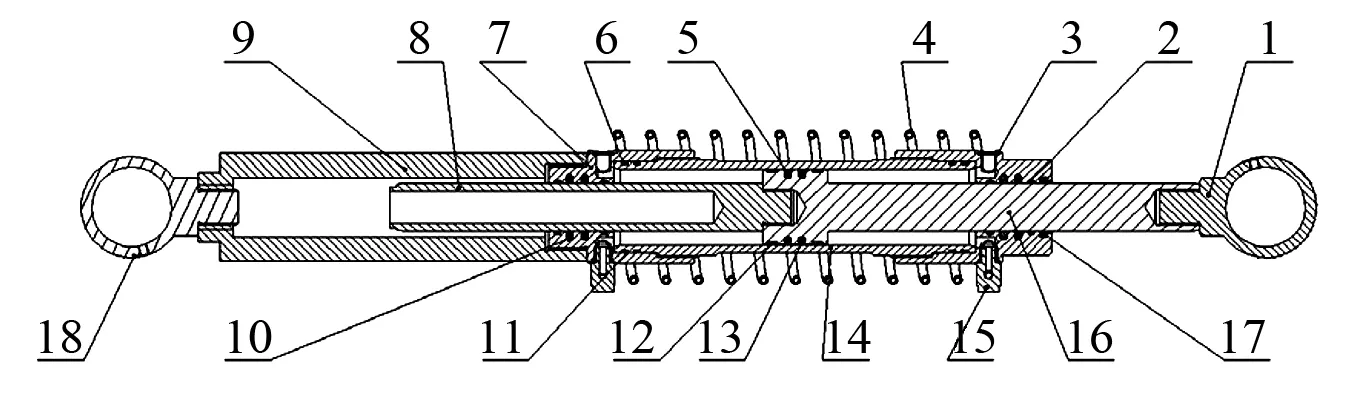
1-铰链A;2-导向带A;3-端盖A;4-螺旋管;5-格莱圈;6-O型圈;7-端盖B;8-活塞杆;9-传力筒;10-斯特封;11-保护圈;12-导向带B;13-T型特康格莱圈;14-缸筒;15-接头总成;16-活塞杆A;17-防尘圈; 18-铰链B图8 外置螺旋管式液力惯容器二维图 Fig.8 engineering drawing of hydraulic inerter with ex-helical tube

验证所研究的液力惯容器的结构功能、工作原理及数学模型的准确性需要对液力惯容器进行行程试验、准静态试验和动态力学特性试验，即选取合适的试验台架对液力惯容器进行行程、准静态及典型频率下的正弦激励；应用与台架相匹配的数据采集与处理系统记录施加给液力惯容器的激振力值随激振位移变化而变化的数据，从而可以得到惯容器对激振头的总的作用力及变化曲线。

验证液力惯容器阻尼力与惯性力的量化关系，需要选取合理的压力传感器获得各试验工况中液压缸两端的压力随时间的变化情况，同时通过相应的数据采集设备和软件对压力值进行完整记录，并在试验结束后进行液力惯容器液压缸两端压力值分析。

对液力惯容器而言，除结构形式和参数外，液体的选择也是液力惯容器设计的关键。液体动力黏度和密度极大地影响液力惯容器的特性，“理想”的惯容器(惯质系数大，阻尼力小)最优的液体应该具备较小的运动黏度和较大的密度，但也要考虑作为试验用油的可行性，我们在第一个液力惯容器的液体选择上选择了常用的矿物油，即10号航空液压油。

2.1 行程试验

液力惯容器行程试验的试验数据以曲线形式表示如图9所示。

图9 1 mm/s行程试验结果 Fig.9 the curve of 1 mm/s stroke testing

液力惯容器活塞由b向c压缩过程中，对应激振器力为CD段，出现微小波动后保持平稳，平均值为-1.698 kN；活塞处于中间位置cd段静止时，对应激振器力值为EF段，力值保持不变，平均值为-0.727 kN；活塞由d向e压缩过程中，对应激振器力为GH段，力值保持不变，平均值为-1.574 kN；活塞处于完全压缩ef段时，对应激振器力为IJ段，力值保持不变，平均值为-0.731 kN。

活塞在缓慢移动过程中激振力值基本维持在-1.580 kN，没有出现剧烈波动，说明液力惯容器结构在工作时没有出现泄漏、卡死等现象，液力惯容器可以正常工作。

2.2 准静态试验

准静态试验数据结果如图10所示。

图10 振幅60 mm，频率0.01 Hz准静态曲线 Fig.10 the quasi-static curve of 60 mm, 0.01 Hz

液力惯容器随着正弦激振出现近似方波周期性响应；在拉伸行程中，对应激振力是为AB段，平均值为0.361 kN；压缩行程中，激振力为CD段，平均值为-1.602 kN。

由理论分析可知，当激励为正弦位移激励时，液力惯容器两端的力应该呈现正弦趋势，本试验测试得到液力惯容器的响应呈近似方波趋势，在压缩或者拉伸行程中力值基本保持不变，因此在0.01 Hz正弦激励下惯容器中存在某一恒力，并起主导作用。

惯容器在拉伸行程和压缩行程激振力值出现不对等、激振力为某一恒力的现象。经过分析可知，惯容器活塞与缸筒接触处的摩擦力、活塞杆上13道密封处的摩擦力、惯容器及工装的重力三个力作用使激振力表现为某一恒力。

假设传力筒受到活塞杆的作用力为摩擦力f1。在整个拉伸过程中，传力筒受到激振台向下的力记F1和惯容器及工装的重力G，同时受到向上的摩擦力f，这三个力作用在传力筒上，使传力筒处于平衡状态，则f1-F1-G=0；同理在整个压缩过程中，有F2-f1-G=0;其中F1的平均值为0.361 kN，F2的平均值为1.602 kN，即惯容器内摩擦力f1约为0.982 kN，惯容器及工装的重力G约为0.621 kN。

通过式(21)计算可得，在0.01 Hz频率下，活塞速度很小，活塞与缸筒接触处的摩擦力接近零，因此摩擦力f1是由活塞杆上13道密封引起。

2.3 力学特性试验

液力惯容器动力学特性试验数据结果如图11所示。

图11 振幅60 mm的各频率力学特性曲线 Fig.11 the force value of 60 mm on different exciting

液力惯容器在激振器正弦位移激励下，激振器力值呈周期性变化，相位相对位移超前四分之一周期；随着激振器激振频率增大，液力惯容器活塞换向后瞬间摩擦力起重要作用的现象一直存在；而在其他时刻摩擦力所占比例减小。

在0.5 Hz正弦激励下，液力惯容器活塞换向后，激振力有微弱波动，如图11(a)中C处所示，随着激振频率增加，激振力波动消失，表现出连续平稳的力学特性。

2.4 力学特性试验与仿真对比

为验证螺旋管式液力惯容器特性数学模型建立的正确性，通过Matlab软件编写螺旋管式液力惯容器力学特性计算模型，采用与试验相同的激励仿真计算，将试验测得激振力与仿真计算求得的惯容器合力进行对比，结果如图12所示。

经过数据统计，图12中各频率激励下，激振器力值和惯容器仿真合力幅值平均值如表1所示。

表1 仿真力值与试验力值对照表Tab.1 the compare of simulating and testing on different exciting

图12 振幅60 mm各频率试验力值与仿真力值对比曲线 Fig.12 the force curves of simulating and testing on different exciting

在1.0 Hz和1.5 Hz激励时，仿真力值的误差分别为3.8%和4.6%，说明仿真力值与试验力值在工程应用允许范围内近似相等。在0.1 Hz激励时，惯容器仿真力值的误差为14.1%，说明其内部存在的摩擦力不可忽略。

在各频率激励下，惯容器换向前时刻均出现激振力值缓慢减小，如图12(b)中A处所示。经过分析可知此时活塞速度为零，惯容器等效阻尼力值近似为零，等效惯性力达到最大值，从而使激振力值出现缓慢减小的现象。

2.5 阻尼力与惯性力量化关系分析

液力惯容器在振幅为60 mm，频率1.0 Hz正弦激励下，惯容器上下腔室压力如图13所示，两腔的压力差如图14所示，惯容器工作时上下腔室压力差发生周期性变化。

图13 上下腔室压力值 Fig.13 the up and down pressure stress of cavity

由公式(2)fΔp=(p2-p1)Ap计算得到液力惯容器试验中的阻尼力与仿真阻尼力对比关系用曲线形式表示如图15所示。通过统计计算，试验阻尼力的最大幅值平均值为30.59 kN，仿真阻尼力的最大幅值平均值为31.53 kN，误差为3%，可以认为仿真阻尼力与试验阻尼力近似相等。

图14 上下腔室压力差 Fig.14 the pressure differential of up and down cavity

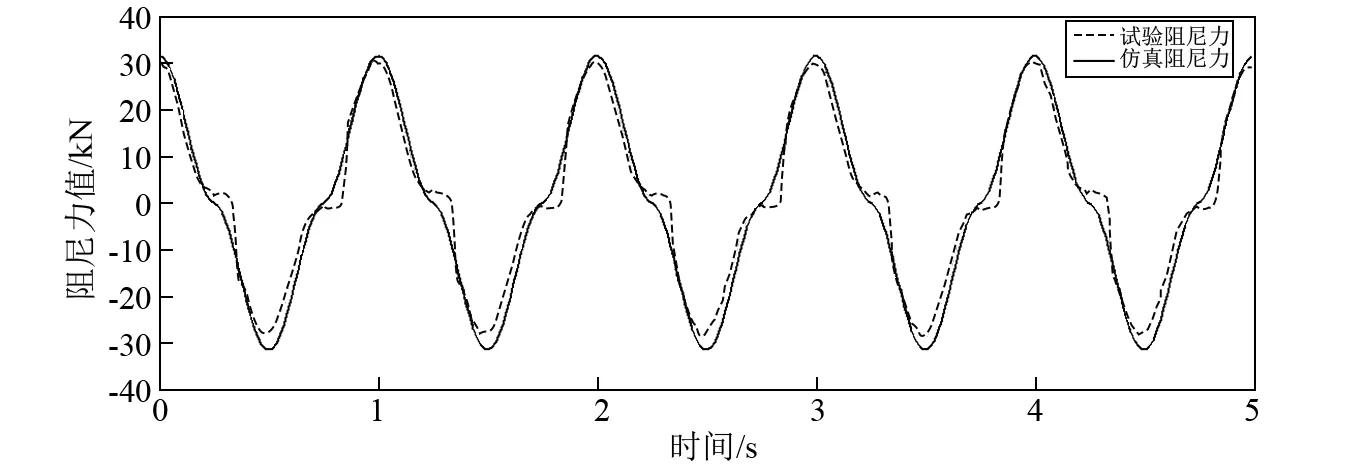
图15 试验阻尼力、仿真阻尼力对比图 Fig.15 the damping force of testing and simulating

液力惯容器试验测得的惯性力与仿真惯性力的对比关系如图16所示。通过统计计算，测得的惯性力最大幅值平均值为1.58 kN，仿真惯性力的最大幅值平均值为1.71 kN，误差为7.6%，可以认为仿真惯性力与试验惯性力近似相等。

图16 试验惯性力、仿真惯性力对比图 Fig.16 the inter force of testing and simulating

3 结 论

(1)外置螺旋管式液力惯容器惯质系数很大，封装的相对惯性(与质量的比)也很大。

(2)外置螺旋管式液力惯容器工作时存在近似定值的摩擦力，当激振频率很小时，阻尼力、惯性力很小，摩擦力占主要成分，随着激励频率增大，摩擦力所占比

例明显减小，此时液力惯容器可以等效为一个阻尼器和一个惯容器的并联结构。

(3)液力惯容器换向冲击小，换向时等效惯性力达到最大值。

(4)选用减振器常用的10号航空油作为液力惯容器的工作液体，使液力惯容器表现出阻尼力相对惯性力较大的特性，因此10号航空液压油不适合作为液力惯容器的工作液体。

(5)理想液力惯容器(只有惯性力，没有阻尼力)中的液体应该是密度足够大，而运动黏度足够小的液体。

[ 1 ] 毛明, 王乐, 陈轶杰，等. 惯容器及惯容器-弹簧-阻尼器悬架研究进展[J]. 兵工学报, 2016(3): 525-534.

MAO Ming, WANG Le, CHEN Yijie et al. Reseach progress in inerter and inerter-spring-damper suspension[J]. Acta Armamentarll, 2016(3): 525-534.

[ 2 ] 陈龙, 张孝良, 汪若尘. 应用惯性蓄能的车辆悬架 [P]. 中国, 发明专利, 专利号: ZL200810123830.8.

[ 3 ] 孙晓强, 陈龙，张孝良，等. 基于ADAMS的滚珠丝杠式ISD悬架平顺性仿真研究[J]. 车辆与动力技术, 2012, 126(2): 1～4.

SUN Xiaoqiang, CHEN Long， ZHANG Xiaoliang，et al. Study of ride comfrt on ball-screw ISD suspension based on ADAMS[J]. Vehicle & Power Technology, 2012, 126(2): 1-4.

[ 4 ] SMITH MALCOLM C. Force-controlling mechanical device: UK PCT/GB02/03056[P]. 2003-01-16.

[ 5 ] 陈龙, 张孝良, 聂佳梅等. 摆线钢球式惯性质量蓄能器[P]. 中国, 发明专利, 申请号: 201010281317.9.

[ 6 ] 林子谦．惯质模型的实现[D]．台北：台湾大学, 2007.

[ 7 ] 张孝良. 理想天棚阻尼的被动实现及其在车辆悬架中的应用[D]. 镇江: 江苏大学, 2012.

[ 8 ] SWIFT S J, SMITH M C, GLOVER A R, et al. Design and modelling of a fluid inerter[J]. International Journal of Control,2013,86(11): 2035-2051.

[ 9 ] JIANG J Z, MATAMOROS-SANCHEZ A Z. Passive suspensions incorporating inerters for railway vehicle[J]. Vehicle System Dynamics, 2012, 50(sup 1): 263-276.

[10] Robin.2011.Fluid inerter :US, PCT/GB2010/000112[P].

[11] RODMAN S, TRENC F. Pressure drop of laminar oil-flow in curved rectangular channels[J]. Experimental Thermal and Fluid Science,2002,26(1): 25-32.

[12] 王积伟. 液压与气压传动[M].北京：机械工业出版社，2005.