三维落角约束自适应分数阶滑模制导律设计*

刘清楷，陈坚，汪立新，秦伟伟

(火箭军工程大学,陕西 西安 710025)

0 引言

多约束制导问题是提高精确武器打击效能的一个重要方面[1]。Kim[2]首次给出满足末端角度约束的次最优制导律方法以来，学者在带有约束的制导问题上，取得了丰硕的成果。

文献[3]将末制导问题转化为带约束条件的最优控制问题，但由于目标高机动性和外界扰动的影响，建立的模型误差较大，造成制导精度较低。而滑模变结构控制对系统参数摄动具有不变性和对外部扰动的鲁棒性，设计滑模面时加入角度约束约束项，得到带角度约束的滑模制导律[4-6]。文献[7-8]采用非奇异终端滑模控制，得到了有限时间收敛的制导律。文献[9]提出了结合最优制导方法和变结构制导方法的复合制导律，但该方法过于复杂，难以进行工程应用。文献[10]研究了利用高增益观测器进行目标加速度的估计方法，取得了较好的效果。

文献[11]将分数阶微积分理论结合比例导引律得到了分数阶微积分比例制导律，但未加入角度约束。屈耀红[12]等将分数阶滑模用于改进传统比例导引，实现了无人机空中加油过程的角度约束，但其受限于加油机为匀速直线飞行的场景。

目前已有的三维制导律大多是直接忽略俯仰通道与偏航通道之间的耦合，本文建立三维弹目相对运动模型，将耦合项作为干扰项，利用扩张状态观测器(extended state obsrever, ESO)进行实时估计，达到解耦的目的。采用分数阶积分器防止积分器饱和现象的出现[13]，引入分数阶微分器来增强控制器的鲁棒性以及削弱抖振。同时设计一种新的滑模趋近律，保证系统状态能够快速收敛到滑模面上，利用ESO对目标机动加速度进行实时估计与补偿，最终得到本文的自适应分数阶滑模导引律(adaptive fractional order sliding mode guidance law, AFOSG)。通过仿真验证，说明本文所设计方法能够削弱抖振，实现偏移量和角度约束。

1 分数阶微积分基本定义

分数阶微积分目前常用的3种定义为：Caputo(C)型、Grünwald-Letnikov(GL)型和Riemann-Liouville(RL)型。其中C型定义的拉普拉斯变换式最为简洁[14]，更为常用。

连续可积函数f(t)的C型分数阶微积分[15]为

(1)

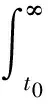
以上可以看出，分数阶微分与过去所有点的信息相关，即记忆性，将其引入到滑模设计中，使其稳定性更强;其次随着时间的增加，权值不断减小，即遗忘性，利用这一特性可减小作用到被控系统上的控制量，达到减小抖振的目的。

2 弹目相对运动模型

由于导弹飞行过程中只能控制正交于速度方向的加速度大小[16]，故先在弹道坐标系建立其动力学方程。如图1所示，图中OxIyIzI为参考惯性系，Mxsyszs为视线坐标系。假设导弹和目标在飞行过程中保持最大速度飞行不变。

导弹和目标在弹道系及航迹系的动力学方程和其在惯性系的质心运动方程[17]为

(2)

(3)

式中：vm为导弹飞行速度;θm为导弹弹道倾角;σm为导弹弹道偏角;vt为目标逃逸速度;φt为目标航迹倾角;ψt为目标航迹偏角。

由文献[18]弹目相对运动模型为

(4)

(5)

(6)

因式(5),(6)形式相近，第3章制导律设计先以式(5)为基础进行设计。

3 带ESO的自适应分数阶滑模制导律设计

3.1 自适应分数阶滑模制导律设计

本文基于零化视线角速率[19]进行制导律设计。传统整数阶积分滑模面[20]为

(7)

本文为利用分数阶微积分算子的记忆性和遗忘性，设计分数阶滑模面如下：

(8)

式中：0<α1<1为分数阶微积分算子的阶次;c11,c12,c13,c14>0为待设计的增益系数。

设计一种新的自适应滑模趋近律如下：

(9)

本文采用误差向量的2-范数作为自适应参数，保证系统的趋近速率保持较大，且避免在接近滑模面时产生抖振。由式(8)和式(9)设计带攻击角约束的自适应分数阶滑模制导律如下：

(10)

式(10)中包含dε总扰动项，根据文献[20]，设计扩张状态观测器如下：

(11)

式中：z13为dε/r的观测值;β11，β12，β13为待设计参数;

式中：δ为线性段的长度。

综合式(10)和式(11)得到含ESO的自适应分数阶滑模制导律如下：

(12)

3.2 稳定性证明

选取Lyapunov函数：

(13)

对式(13)求导可得

2S1[c11e12+c12Dα1e12+c13Dα1e11-

将式(12)带入上式整理得

当β11，β12，β13选取合适的值时，式(11)的观测误差趋于0[21]，即观测值z13以有限时间收敛于dε/r的邻域内，则有

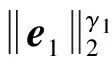
由文献[22]可得，系统状态是有限时间收敛的，且收敛到滑模面S1=0的时间为

(14)

式中：e12≠0;S1(0)为S1的初值。

当e12=0的时，将式(12)代入式(5)整理得：

(15)

由式(15)可得，e12=0不是稳定状态，故系统状态能够在有限时间内收敛到滑模面S1=0。

当S1=0时，得到滑模面动力学方程：

(16)

对式(16)进行Laplace变换[23]得到

c11E(s)+c12sα1E(s)+c13sα1-1E(s)+c14sE(s)=0.

上式可以看作是描述以e11(t)为输出的闭环系统的方程，其开环传递函数可以表示为

上式中0<1-α1<1;c11，c12，c13，c14>0;开环传递函数的相位总是大于-π/2，且不含右半平面的极点，由Nyquist稳定判据可以得到原闭环系统是稳定的，即e11(t)是收敛的。同时由分数阶系统Laplace变换的终值定理[24]，可以得到

c14s2-α1)/c11s1-α1=0.

综上，本文自适应分数阶滑模导引律能够使系统状态渐进收敛到滑模面，弹目视线角误差e11(t)和视线角速率e12(t)能渐进收敛到0。

为减小抖振，将式(12)中的符号函数，用饱和函数替代，得到制导律：

(17)

式中：

ω为边界层厚度，通过调节其值以削减抖振。

同样由式(6)可以得到：

amzs= -cosε[c21re22+c22rDα2e22+

(18)

(19)

4 仿真验证

为证明本文导引律的可行性，将新型自适应分数阶滑模制导律与增强比例导引律(augmented propotional navigation guidance law,APNG)以及非奇异终端滑模导引律(nonsingular terminal sliding mode guidance law，NTSMG)进行对比仿真。导弹初始位置(500,0,-1 500)m，目标初始位置(3 000,5 000,1 000)m，导弹速度为vm=800 m/s，目标速度为vt=300 m/s，导弹初始弹道倾角为θm0=π/3 rad，初始弹道偏角为σm0=-π/10 rad，目标初始航迹倾角为φt0=π/4 rad，初始航迹偏角为ψt0=-π/6 rad。AFOSMG的参数为简单起见，2个方向制导律中同一位置的参数大小相等，即c11=c21=400，c12=150，c13=300，c14=1，k11=260，k12=200，α1=0.45，β11=100，β12=300，β13=1 000，δ=0.01，ω=0.01。利用文献[25]的FOMCON工具箱进行分数阶微积分的计算。APNG定义为

(20)

(21)

式中：N=4。

由于APNG需要获取目标的精确机动信息，本文在利用此方法仿真时认为该信息为已知。NTSMG定义为

(22)

(23)

导引律在视线系中定义，需要将其转换到弹道坐标系中，由于篇幅所限，具体方法见文献[26]。

4.1 仿真1

目标机动加速度为atyd=atzd=5g;期望视线角为εd=π/3 rad，ηd=-2π/9 rad。分别采用3种导引律进行仿真，得到结果如图2～4所示。

从图4可以看出，APNG和NTSMG得到的加速度指令均存在一定程度的跳变或振荡，而AFOSMG的加速度指令则保持平稳变化。仿真的脱靶量和末端角度如表1所示。

导引律偏移量/m视线倾角/(°)视线偏角/(°)APNG0．15748．79-49．11NTSMG0．26558．24-41．85AFOSMG0．13359．33-39．97

从表1中可以看出在目标进行常值机动时，本文所设计的AFOSMG导引律无论是在偏移量还是角度偏差均要小于APNG和 NTSMG，证明本文导引律有较好的效果。

4.2 仿真2

当目标进行正弦机动时，atyd=80 sin 0.2t，atzd=80cos 0.2t;期望视线角为εd=π/3 rad，ηd=-π/3 rad。同样进行仿真得到结果如图5～7所示。

从表2中可以看出，相对于其他2种导引律,本文方法无论是偏移量还是末端角度都得到了更高的精度。而且从图7a)和图7b)导弹加速度指令信号变化中可以看出，AFOSMG加速度变化更为平稳，未出现抖振现象。

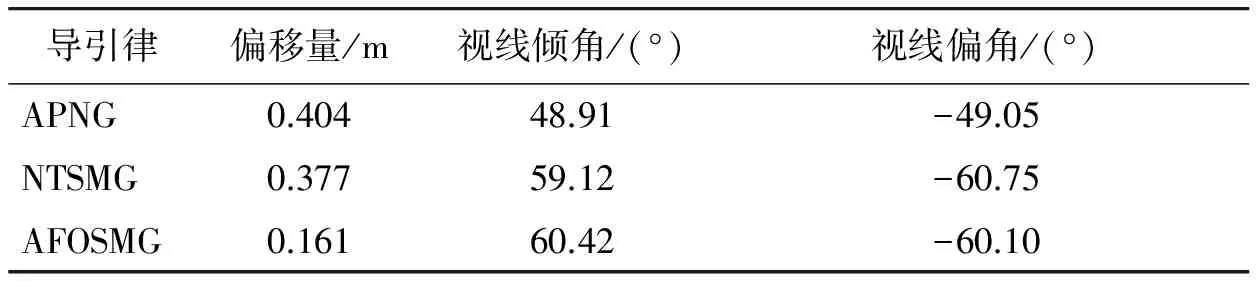
导引律偏移量/m视线倾角/(°)视线偏角/(°)APNG0．40448．91-49．05NTSMG0．37759．12-60．75AFOSMG0．16160．42-60．10

5 结论

本文将分数阶微积分算子引入滑模面的设计，采用一种自适应趋近律得到本文三维AFOSMG，并通过理论证明和仿真实验验证了方法的有效性。

(1) 采用分数阶微积分算子进行滑模面的设计，利用了其记忆性和遗忘性，有效削弱了滑模控制的抖振现象;选取的自适应趋近律能够有效根据系统状态与平衡点的距离，调节速率，并通过Lyapunov稳定性定理对本文的导引律的收敛性进行了证明。

(2) 通过仿真比较，本文的导引律能使导弹的加速度指令更为平稳，降低对导弹过载的要求。

(3) 分数阶微积分的运算耗时较长，但随着弹载机的计算能力增强，其工程应用将不再困难。

本文在制导律设计时，将导弹自动驾驶仪作为理想环节，未考虑其的动态特性，可以在下一步的工作中加以研究;其次本文只是在滑模面的设计中引入了分数阶微积分算子，可以尝试将其引入趋近律的设计中，设计一种新的分数阶滑模趋近律。

参考文献：

[1] 李庆春,张文生,韩刚.终端约束条件下末端制导律研究综述[J].控制理论与应用,2016,33(1):1-12.

LI Qing-chun,ZHANG Wen-sheng,HANG Gang.Review of Terminal Guidance Law with Terminal Constraints[J].Control Theory and Applications,2016,33(1):1-12.

[2] KIM M,GRIDER K V.Terminal Guidance for Impact Attitude Angle Constrained Flight Trajectories[J].IEEE Transactions on Aerospace & Electronic Systems,1973,AES-9(6):852-859.

[3] LEE Y I,KIM S H,TANHK M J.Optimality of Linear Time-Varying Guidance for Impact Angle Control[J].IEEE Transactions on Aerospace & Electronic Systems,2012,48(4):2802-2817.

[4] TAO C,WANG S,MING Y.Angular Constrained Guidance Law and Its Optimization with Hybrid Optimization Algorithm[C]∥Guidance,Navigation and Control Conference,IEEE,2014:2455-2460.

[5] 吴鹏,杨明.带终端攻击角度约束的变结构制导律[J].固体火箭技术,2008,31(2):116-120.

WU Peng,YANG Ming.Variable Structure Guidance Law with Terminal Attack Angle Constraint[J].Journal of Solid Rocket Technology,2008,31(2):116-120.

[6] LEE C H,KIM T H,TAHK M J,et al.Design of Guidance Law for Passive Homing Missile Using Sliding Mode Control[C]∥International Conference on Control Automation and Systems,IEEE,2010:2380-2385.

[7] 周慧波,宋申民,刘海坤.具有攻击角约束的非奇异终端滑模导引律设计[J].中国惯性技术学报,2014,22(5):606-618.

ZHOU Hui-bo,SONG Shen-min,LIU Hai-kun.Nonsingular Terminal Sliding Mode Guidance Law with Impact Angle Constraint[J].Journal of Chinese Inertial Technology,2014,22(5):606-618.

[8] 熊少锋,王卫红,王森.带攻击角度约束的非奇异快速终端滑模制导律[J].控制理论与应用,2014,31(3):269-278.

XIONG Shao-feng,WANG Wei-hong,WANG Sen.Nonsingular Fast Terminal Sliding-Mode Guidance with Intercept Angle Constraint[J].Control Theory and Applications,2014,31(3):269-278.

[9] HU Z,TANG X,WANG Y.A 3-Dimensional Robust Guidance Law with Impact Angle Constraint[C]∥Chinese Control and Decision Conference,IEEE,2011:999-1006.

[10] 马克茂,贺风华,姚郁.目标机动加速度的估计与导引律实现[J].宇航学报,2009,30(6):2213-2219.

MA Ke-mao,HE Femg-hua,YAO Yu.Estimation of Target Maneuver Acceleration and Guidance Law Implementation in Homing Terminal Guidance[J].Journal of Astronautics,2009,30(6):2213-2219.

[11] 叶继坤,韦道知,李炯,等.基于分数阶微积分理论的新型三维末制导律[J].固体火箭技术,2016(3):428-435.

YE Ji-kun,WEI Dao-zhi,LI Jiong,et al.Novel 3D Terminal Guidance Law Based on the Theory of Fractional Order Calculus[J].Journal of Solid Rocket Technology,2016(3):428-435.

[12] 屈耀红,余自权,张友民.无人机空中加油过程中分数阶滑模会合导引控制[J].控制理论与应用,2015,32(11):1464-1469.

QU Yao-hong,YU Zi-quan,ZHANG You-min.Fractional-Order Sliding-Mode Guidance Control for Rendezvous of Unmanned Aerial Vehicles During Air Refueling[J].Control Theory and Applications,2015,32(11):1464-1469.

[13] JOHANASTROM K,RUNDQWIST L.Integrator Windup and How to Avoid It[C]∥American Control Conference,IEEE,1989:1693-1698.

[14] SHAKOOR P,RICARDO A,DELFIM F M T.Numerical Approximations of Fractional Derivatives with Applications[J].Asian Journal of Control,2012,15(3):698-712.

[16] 佘文学,周凤岐.三维非线性变结构寻的制导律[J].宇航学报,2004,25(6):681-685.

SHE Wen-xue,ZHOU Feng-qi.High Precision 3-D Nonlinear Variable Structure Guidance Law for Homing Missile[J].Journal of Astronautics,2004,25(6):681-685.

[17] 严晗,季海波.弹道坐标中三维鲁棒非线性导引律[J].控制理论与应用,2013,30(9):1079-1085.

YAN Han,JI Hai-bo.Three-Dimensional Robust Nonlinear Guidance Law in Trajectory Coordinates[J].Control Theory and Applications,2013,30(9):1079-1085.

[18] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京：北京理工大学出版社,2000.

QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.The Flight Dynanmics of Missiles[M].Beijing:Beijing Institute of Technology Press,2000.

[19] 刘金琨.滑模变结构控制MATLAB仿真[M].2版.北京:清华大学出版社,2012.

LIU Jin-kun.Sliding Mode Control Design and MATLAB Simulation[M].2nd ed.Beijing:Tsinghua University Press,2012.

[20] 雷虎民,王华吉,周觐,等.基于扩张观测器的三维动态面导引律[J].系统工程与电子技术,2017,39(1):138-146.

LEI Hu-min,WANG Hua-Ji,ZHOU Jin,et al.Three-Dimensional Dynamic Surface Guidance Law Based on Extended State Observer[J].Systems Engineering and Electronics,2017,39(1):138-146.

[21] 韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].北京：国防工业出版社,2008.

HAN Jing-qing.Active Disturbance Rejection Control Technique—the Technique for Estimating and Compensating the Uncertainties[M].Beijing：National Defense Industry Press,2008.

[22] BHAT S P,BERNSTEIN D S.Finite-Time Stability of Continuous Autonomous Systems[J].Siam Journal on Control & Optimization,2000,38(3):751-766.

[23] YU S,YU X,SHIRINZADEH B,et al.Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode[C]∥Information Fusion,2003,Proceedings of the Sixth International Conference of IEEE,2003:1433-1440.

[24] MILLER K,ROSS B.An Introduction to the Fractional Calculus Fractional Differential Equations[M].New York:Wiley,1993.

[25] TEPLJAKOV A.FOMCON:Fractional-Order Modeling and Control Toolbox[C]∥Mixed Design of Integrated Circuits and Systems,IEEE,2011:684-689.

[26] SUN Chang-yin，MU Chao-xu，YU Yao.Some Control Problems for Near Space Hypersonic Vehicles[J].ACTA Automatica Sinica,2013,39(11):1901-1913.