新灰色组合模型在沉降变形预测中的作用

2018-04-27张文祥黄张裕于小桐张君儒

地理空间信息 2018年4期

张文祥，黄张裕，于小桐，王彬，张君儒

（1.河海大学地球科学与工程学院，江苏南京211100）

基于建筑物沉降的系统性变化规律，运用可靠的方法，科学、准确、实时地描述建构筑物的沉降变化趋势，从而对人民财产安全提供保障。单一的预测模型具有一定的局限性，传统的GM(1,1)模型主要适用于单一的指数增长模型［1］，对沉降序列数据出现的异常情况很难预测。可以综合利用不同预测模型的优势，从而构成具有较高预测精度的组合预测模型［2］。

国内外关于GM(1,1)模型的研究较多［3-7］，众多学者也依据灰色理论提出了较多的改进模型，如灰色模型与多项式拟合模型的组合、灰色模型与神经网络模型的组合等。本文将传统GM(1,1)模型、初始值修正、背景值优化及组合模型预测数据作为B样条曲线函数的4个型值点［10,12］，确定曲线拟合函数，结合某建筑物沉降监测实例来进行沉降序列的拟合和预测。

1 改进的GM(1,1)模型

单一的传统GM(1,1)模型的预测效果取决于模型的结构参数，随着GM(1,1)模型广泛应用于建筑物等沉降预测中，并取得较多成功的预测作用，在一定程度上为建筑物的实时安全性监测、预测提供了指导，但传统的GM（1,1）模型可能存在一定的预测偏差，主要原因有：①不同程度的指数序列需求的背景值不同；②传统的GM(1,1)模型采用x=x0

(1)的初始条件时，丢失了以新信息数据进行预测的特性。本文从背景值、初始值入手，着重探究两者优化后的数据，并将其作为B样条曲线型值点的研究对象。

1.1 背景值优化

用Sn作为区间[k,k+1]上的背景值

式中，需要确定常数n，对于不同程度的数值序列，需要确定不同的数值。针对预测模型的确立，应根据实际测量数据确定待定常数，也就是依据不同的数据序列确定不同的背景值，更加合理地适用于沉降变形预测模型的建立［10］。

1）对低增长序列，有：

2）对高增长序列，有：

待定常数的确定取决于数据序列的增值速率及变化。一般来说，建筑物的沉降变形较缓慢，因此在本文中待定常数的确定采用低增长序列的参数模型即式（3）。依据实际数据序列确定的待定常数n，可近似逼近实际数据序列，更能够反映建筑物沉降变形规律。

1.2 初始值修正

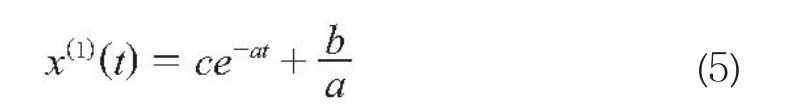
分别令t=1、n，可得：

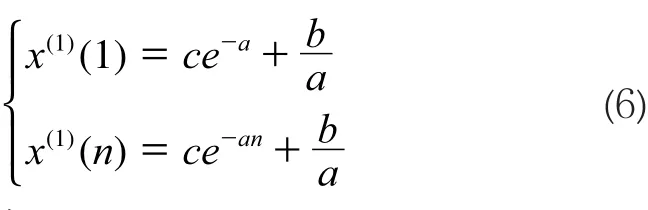
从而得到c的表达式：

只要得到数据预测模型中的c值，将能够有效得到初始值修正后的沉降预测值。考虑到新预测值而不使用原有第一期沉降数据，保留灰色模型的新信息可靠性，能够较好地反映建筑物沉降预测规律。

1.3 基于初始值修正及背景值优化相关性确定权系数

基于优化后的预测数据作为研究对象，以初始值修正、背景值优化后的数据的相关性确定权系数，建立线性方程式，确定组合模型的未知项系数，得到优化后的数据。具体模型如下：初值修正的模型预测数景值优化的模型预测数据用两者建立线性组合模型［7］：

根据误差传播定律得到预测值的组合模型方差为：

实际计算中，e1、e2的计算是相互独立的，故可以认为cov(e1,e2)。当D(e)最小时，则有：

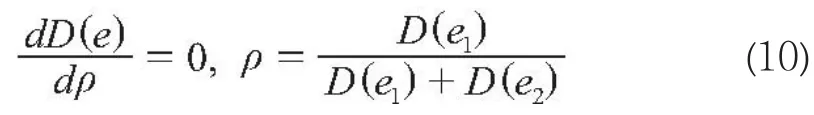
根据（10）计算ρ值，得出背景值优化与初值修正组合模型的系数。

2 B样条曲线模型

常用的B样条曲线因其连续性、局部性，而广泛应用于各类曲线的拟合。本文基于B样条曲线的基本思想，将传统GM（1，1）模型预测数据、背景值优化、初始值修正及组合模型的预测数据作为B样条曲线的型值点，进行新的预测曲线拟合，既可以保留预测模型短期预测精度高、也保留了B样条曲线局部连续的特点，得到较优的新灰色组合模型。

2.1 B样条函数模型

传统的样条曲线拟合是每4个点拟合成一条曲线，其具有连续性、局部性、凸包性的特点，B样条曲线拟合的方程为：

式中，Pi是特征多边形顶点，也称控制顶点，Bi为基函数。具体表示为：

2.2 基本思想

将传统GM(1,1)模型、初始值修正、背景值优化后以及组合模型数据作为曲线的型值点，进行预测曲线拟合，得到新的预测值拟合曲线。将两种优化后的预测数据依据监测周期的推进，分别作为型值点P1、P2、P3和P4。在曲线拟合过程中仅改变一个控制顶点，只会影响局部拟合曲线，能够满足建筑物变形短期预测的目的，并且拟合曲线在端点处连续，若干预测曲线构成一段完整的预测B样条曲线，如图1所示。

图1 B样条曲线基本图示

3 实例分析

为了验证4种预测数据作为B样条曲线型值点所拟合预测曲线的效果，选用某厂房建筑物的沉降监测数据进行分析。该建筑物共31个测点，并定期对建筑物监测点进行沉降监测，共监测10期。以沉降监测点C06为例作为实验验证对象，其原始沉降监测数据见表1。

表1 C06沉降监测点的沉降监测数据

利用Matlab软件进行计算，得出初始值修正数据、背景值优化数据，依据文中的组合模型确定两者的权系数分别是0.499和0.501，两组数据的方差分别是0.120 4和0.120 9，从而得出每一期组合模型的预测值。以上述4种数据作为B样条函数的型值点，既可以保留前3者预测模型的优势，又具备建筑物短期预测效果好的特点，能够更加逼近建筑物的实际变形，达到较好的预测效果。通过上述数据的组合，得到C06点的预测数据见下表2，第一期数据均为0.68 mm，故保留0.68 mm。

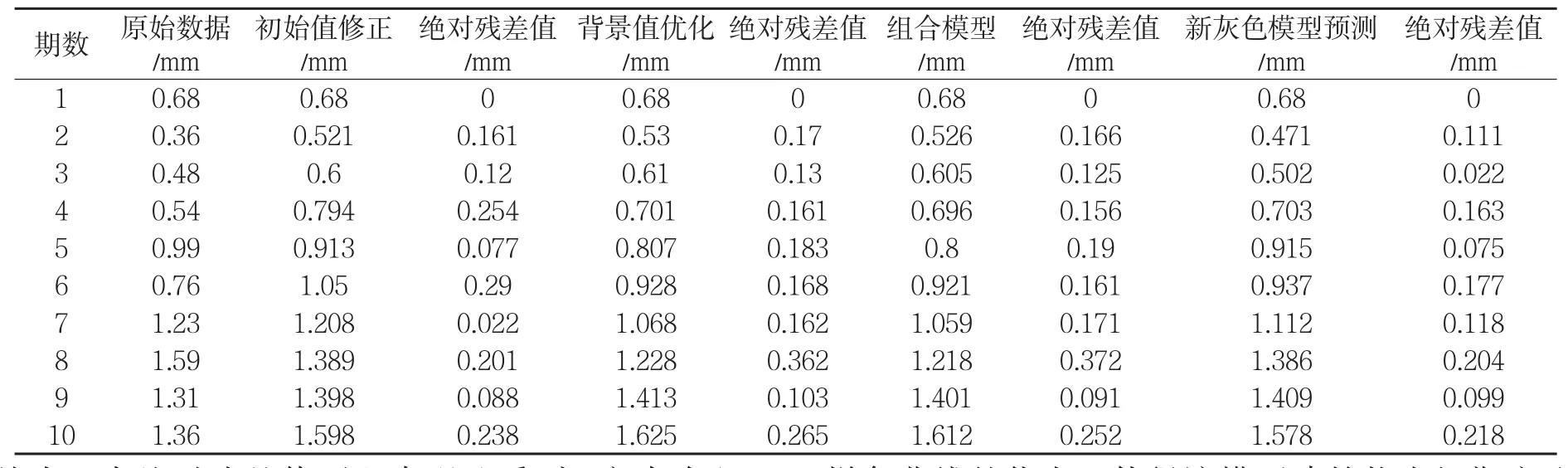
表2 C06沉降监测点各种模型预测值及绝对残差值

从表3中绝对残差值可以直观地看到，新灰色组合模型的预测精度较前几种模式预测精度高。在传统模型中，预测精度会随着监测周期的增加，预测精度逐渐降低；依据初始值修正、背景值优化后的数据相关性确定的组合模型预测精度较传统模型预测精度高；而文中提出的新灰色组合模型在后几期预测过程中，均取得了较好的预测效果。

将沉降原始沉降序列、传统GM(1,1)模型、组合模型及新灰色组合模型的预测值绘制成图2，可以看出：①虽然基于背景值优化、初始值修正的方差确定权系数的组合模型预测精度较高，但是拟合曲线较为平滑，严重脱离实际沉降监测序列；②新灰色模型的预测值与实际测量值的逼近程度更加明显，特别是在第5、8期预测数据与实际测量序列偏差较小，其他模型偏差较大。