基于建筑角点的机载和车载点云数据配准
2018-04-27钟若飞孙海丽
曾 卓,钟若飞,孙海丽
(1.首都师范大学 北京成像技术高精尖创新中心 ,北京 100048;2.首都师范大学 资源环境与旅游学院 ,北京100048;3.首都师范大学 三维数据获取与应用重点实验室,北京100048)
建筑物是地理空间中一种常见的人文景观,其形状规则、特征明显、易于区分。角点作为建筑轮廓线的交点,是一种良好的配准基元,如何获取高精度的角点对配准结果至关重要。本文提出一种提取建筑角点的新方法,采用该方法提取高精度的同名建筑角点,从而实现机载和车载点云数据的配准[1-5]。
1 同名建筑角点提取
在提取同名建筑角点时,先采用平面投影的方式提取角点的二维平面坐标,再运用数学方法解算出角点的第三维坐标。建筑角点提取的流程如图1所示。首先运用RANSAC算法提取得到建筑物的顶面和立面点云,用最小二乘法拟合出建筑物顶面和立面方程;再将提取到的顶面点云投影到xoy平面上,立面点云投影到yoz平面上,通过Alpha Shape算法检测投影平面上的建筑轮廓,之后对平面上的建筑轮廓线进行最小二乘拟合,轮廓线交点的坐标即为建筑角点在该平面上的二维坐标;最后将角点的二维坐标分别代入对应的平面方程,计算得到建筑角点的第三维坐标。

图1 建筑角点提取流程
1.1 建筑面片点云提取
RANSAC算法是根据一组包含异常数据的样本数据集,计算出数据的数学模型参数,得到有效样本数据[6]。RANSAC算法提取平面点云的过程如下:
1)在原始点云中任取3个点,判断这3个点是否共线,如果共线,再重新随机选取3个点,直到不共线为止,计算不共线的3点确定的平面方程ax+by+cz+d=0;
2)计算其余点到该平面的距离:

3)选取阈值t=σ,σ为其余点到平面距离的标准偏差,当di>σ时被认为是异常数据,反之则为有效数据,统计有效数据的个数m;
4)重复上面的步骤,迭代k次,用m最大时的数据点表达该平面。
1.2 建筑面片平面投影轮廓提取
建筑面片的轮廓线反映了建筑物的结构特征,轮廓线的交点即为建筑物的角点。Edelsbrunner等在1983年提出的Alpha Shape算法能够有效提取离散点集的边缘轮廓[7],如图2所示。该算法原理是:用一个半径为α的圆在点集S外滚动,当半径α足够大时,该圆就不会滚到点集S内部,此时该圆的滚动轨迹就是点集S的边界。国内外也有不少学者利用Alpha Shape算法从机载点云数据中提取建筑物轮廓线;李鹏程等在建筑物轮廓提取的实验中得出,α取点云数据平均间距3倍时,效果最好[8]。

图2 Alpha Shape算法原理
1.3 建筑角点三维坐标计算
本文通过最小二乘法拟合建筑面片的平面方程以及在二维平面上投影的轮廓线方程来计算角点的三维坐标。角点坐标的计算思想如图3所示。首先对RANSAC算法提取到的建筑面片点云进行最小二乘平面拟合,将拟合得到的平面标记为P;然后对Alpha Shape算法提取到的投影轮廓线进行最小二乘直线拟合,将拟合得到的直线标记为l1和l2;求解直线l1和l2的交点,记为p'(x0,y0),p'即为建筑角点在二维平面上的投影点;将点p'坐标代入平面P的方程解算得到第三维坐标z0,则p(x0,y0,z0)即为建筑角点的三维坐标。
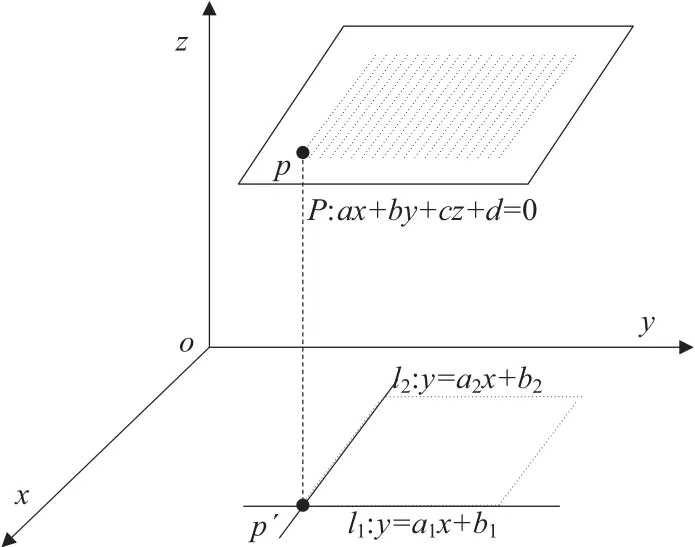
图3 建筑角点坐标计算
2 点云数据配准
机载和车载点云数据配准的实质是两种点云数据集之间的一种刚性变换。设(xi,yi,zi)和(Xi,Yi,Zi)表示的是i点分别在空间直角坐标系o-xyz和O-XYZ中的坐标,则O-XYZ坐标系中的点向o-xyz坐标系转换的数学模型为[9]:
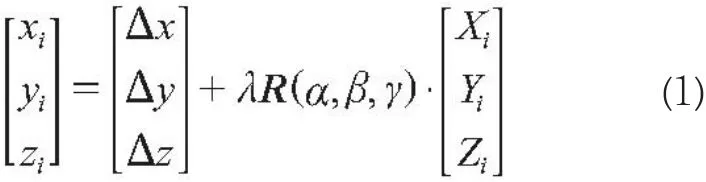
其中,R(α,β,γ)=RαRβRγ。式(1)中,Δx、Δy、Δz分别是x轴、y轴、z轴方向上的平移量;α、β、γ分别是绕x轴、y轴、z轴的旋转量;λ为缩放系数。由于机载点云和车载点云数据之间是一种刚性配准,因此缩放系数为1,即无尺度变换。
在获得同名建筑角点的基础上,采用六参数转换模型计算机载点云数据的3个旋转参数α、β、γ和3个平移参数Δx、Δy、Δz,利用得到的转换参数对机载数据进行旋转和平移变换,实现机载和车载点云数据的配准。
3 实验与分析
3.1 实验数据
实验所用数据由首都师范大学所研制的机载车载一体化移动测量系统于2015-12-30在湖北麻城市扫描获取。本研究截取800 m×600 m范围的数据作为试验数据,如图4所示。其中,机载点云数据平均点间距为0.6 m,车载点云数据平均点间距为0.15 m。

图4 原始点云数据
3.2 实验过程
3.2.1 同名建筑角点提取
本文在配准过程中,通过RANSAC算法提取得到分布均匀的10座建筑的顶面点云和立面点云,并用最小二乘法对其进行平面拟合,拟合的平面方程如表1、2所示。然后将提取到的顶面点云投影到xoy平面上,立面点云投影到yoz平面上,用Alpha Shape算法提取得到投影平面上的点云轮廓,并对相交得到建筑角点的两条轮廓线进行最小二乘直线拟合,拟合的直线方程如表3、4所示。解算出拟合的两条相交直线的交点坐标,即为建筑角点在该二维平面上的平面坐标,将平面坐标代入对应的平面方程,计算得到角点的第三维坐标。提取得到的同名建筑角点坐标如表5所示。
3.2.2 机载和车载点云数据配准
鉴于点云数据绝对坐标值较大,为避免计算转换参数时出现奇异矩阵,先对原始点云数据和提取的角点坐标进行整体平移。将x坐标减去591 500,y坐标减去3 448 000,利用整体平移后的同名建筑角点,解算平移后的机载点云数据的转换参数,如表6所示。根据转换参数,对平移后的机载点云数据进行转换,再把经转换后的点云数据平移回去,即x坐标加591 500,y坐标加3 448 000,最终实现两种数据的配准。

表1 建筑顶面拟合方程
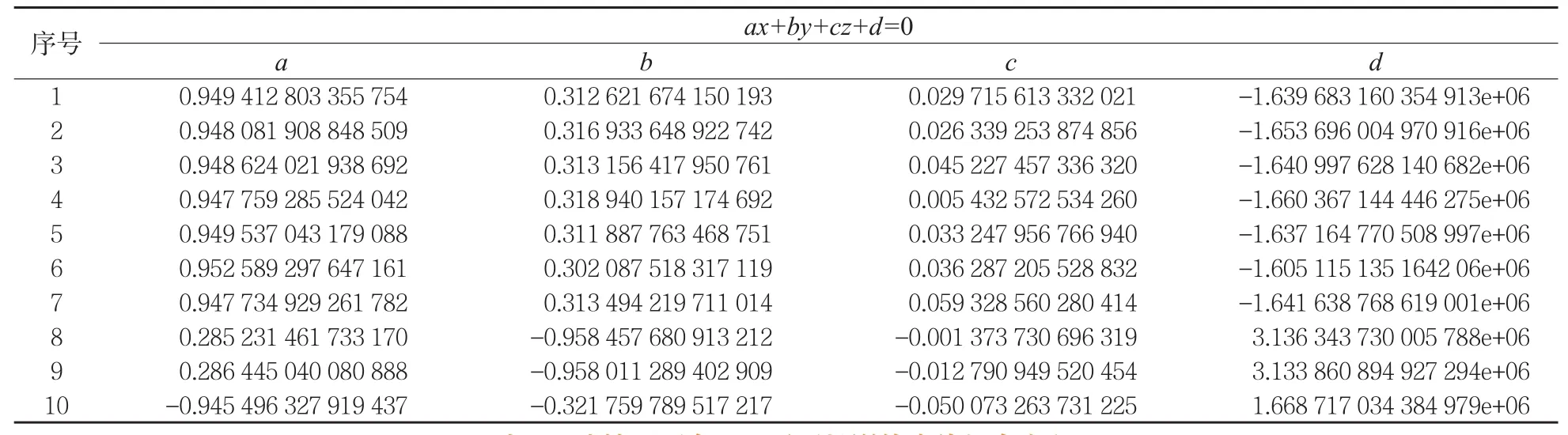
表2 建筑立面拟合方程
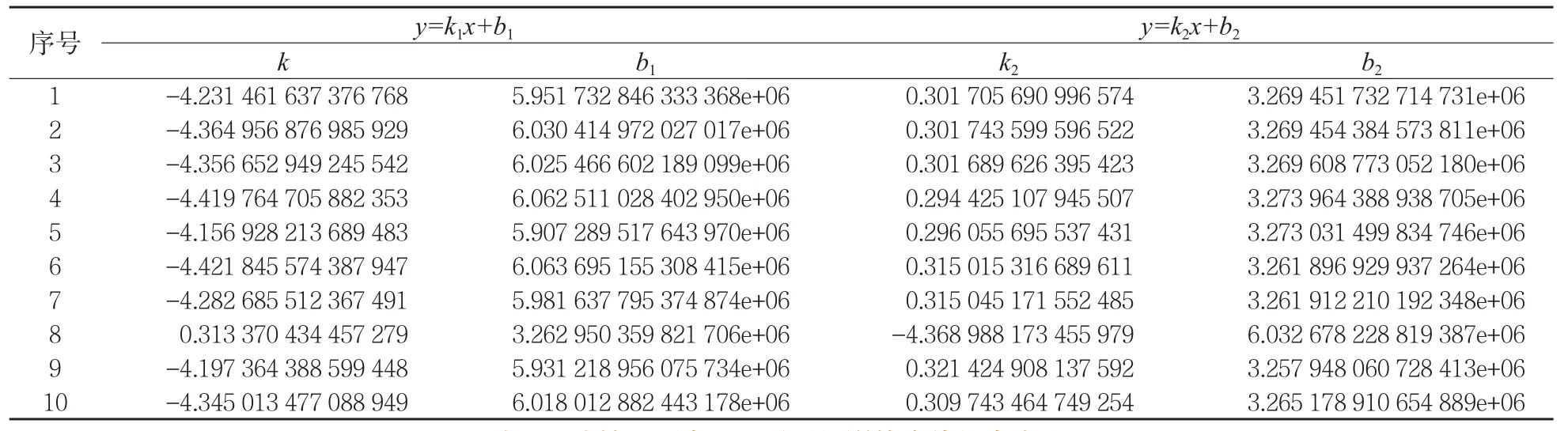
表3 建筑顶面在xoy平面投影轮廓线拟合方程

表4 建筑立面在yoz平面投影轮廓线拟合方程

表5 同名建筑角点提取结果

表6 机载点云数据转换参数
3.3 结果分析与精度评价
图5为机载和车载点云数据配准结果,绿色点云为机载数据,橙色点云为车载数据。从整体配准结果来看,建筑物的侧面车载点云数据和顶面机载点云数据已经较好地融合在一起。

图5 机载和车载点云数据配准
首先选取几何特征明显的建筑轮廓线和道路边缘线,对比配准前和配准后轮廓线的吻合程度,作为平面配准精度评价依据。如图6、7所示,绿色点云为车载激光数据,白色点云为机载激光数据,配准前两种数据所表示的建筑轮廓线和道路边缘线间隙较大,吻合程度较低。通过量测,配准前建筑轮廓线平均偏离2.321 m(图6a),道路边缘线平均偏离2.284 m(图7a)。配准后,可以清晰地看出轮廓线吻合程度较好。通过量测,配准后建筑轮廓线平均间距为0.122 m(图6b),道路边缘线平均间距为0.118 m(图7b)。

图6 建筑轮廓线配准效果图

图7 道路边缘线配准效果图
边缘轮廓线的吻合程度仅能从平面位置上评价数据配准的精度,为了客观评价数据在高程上的配准情况,分别对配准前后的点云数据绘制剖面线,通过对比配准前后的点云剖面图来评价高程配准精度。
图8a为配准前绘制的剖面线,图8b为配准后在同一位置绘制的剖面线,其中蓝色点云为车载激光数据,红色点云为机载激光数据。从图8a可以看出配准前的机载点云数据和车载点云数据在平面上和高程上都有一定的偏差。经量测,平面位置偏差在2.3 m左右,高程偏差在1.5 m左右。从图8b可以看出,配准后,点云在平面和高程上的偏差得到纠正,缩小至0.108 m,高低起伏的地表完全融合到了一起,具有较高的配准精度。

图8 点云剖面图
4 结 语
提出一种基于建筑角点的机载和车载点云数据配准方法。该方法能够有效地提取高精度的建筑角点,将点云数据的配准精度由m级提高到dm级,实现机载和车载点云数据的精确配准。由于该方法是基于建筑角点的特征匹配,对于测区内建筑数量少、分布不均匀的情况,会使配准结果出现局部最优。因此,下一步的研究将对配准结果进行全局优化,进而实现机载、车载点云数据的最优匹配。
[1] 李永强,刘会云,曹鸿,等.基于空-地多源数据融合的建筑物精细建模研究[J].测绘工程,2015,24(8):1-4
[2] Kedzierski M,Fryskowska A.Terrestrial and Aerial Laser Scanning Data Integration Using Wavelet Analysis for the Purpose of 3D Building Modeling[J].Sensors,2014,14(7): 12 070-12 092
[3] Teo T A,Huang S H.Surface-Based Registration of Airborne and Terrestrial Mobile LiDAR Point Clouds[J].Remote Sensing,2014,6(12): 12 686-12 707
[4] Cheng L, Wu Y, Tong L, et al. Hierarchical Registration Method for Airborne and Vehicle LiDAR Point Cloud[J].Remote Sensing, 2015, 7(10):13 921-13 944
[5] 童礼华.多平台点云点云数据集成技术研究[D].南京:南京大学,2014
[6] Fischler M A,Bolles R C.Random Sample Consensus:A Paradigm for Model Fitting with Applications To Image Analysis and Automated Cartography[J]. Communication of the ACM,1980,24(6):381-395
[7] Edelsbrunner H,Kirkpatrick D, Seidel R.On the Shape of a Set of Points in the Plane[J].IEEE Transactions on Information Theory,1983,29(4):551-559
[8] 李鹏程,邢帅,徐青,等.关键点检测的复杂建筑物模型自动重建[J].遥感学报, 2014, 18(6):1 237-1 246
[9] 姚宜斌,黄书华,张良,等.求解三维坐标转换参数的整体最小二乘新方法[J].武汉大学学报:信息科学版,2015,40(7):853-857
