船舶减摇鳍/水舱联合控制技术研究

刘胜 韩研

（哈尔滨工程大学自动化学院，哈尔滨，150001）

在众多的船舶减摇装置中，减摇鳍和减摇水舱普遍被人们应用于船舶减横摇领域，但是它们自身都存在一定局限。减摇鳍在船舶航速较高时可以明显有效地减摇，但在低航速或者零航速下的减摇效果很差甚至没有减摇效果；减摇水舱在任何航速下都有减摇作用，但其减摇效率相对较低，并且在低频扰动下易增摇[1-6]。因此，为了满足船舶在全航速下都能够达到期望的减摇效果，采用减摇鳍和减摇水舱联合减摇的方案，将二者组成船舶减摇鳍/水舱联合控制系统，就可以达到两种减摇装置的互补，从而实现船舶在任何航态下都具有明显的减摇效果。

近年来，国内外的研究主要集中在装备单一减摇装置的减摇效果研究上，对联合减摇装置，尤其是减摇鳍和减摇水舱的联合控制技术上研究甚少。金鸿章和赵为平等人对鳍舱联合减摇进行了理论分析，证明其减摇的可行性。中船重工七〇四研究所在 2015年研制出了“减摇鳍-减摇水舱联合控制器”，可以通过用户选择“联合”和“独立”两种工作模式来切换控制方式，但实际使用采取用户手动切换方式，没有给出何时切换控制能够达到最优控制效果。目前国内外有关舱鳍联合控制的研究中，采用的控制方式都是单独对减摇鳍施加控制，对减摇水舱却没有施加任何控制，这并不能够使“舱鳍联合控制”达到最优的控制效果[7-12]。本文以“船舶减摇鳍/水舱联合控制系统”（后文简称联合系统）为对象，进行了联合控制技术的研究。

1 鳍/水舱联合控制系统数学模型

当船舶同时装备减摇鳍和被动式减摇水舱时，联合系统的数学模型为：

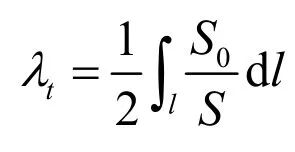
根据减摇鳍控制的动力学机理, 有：

其中，αw为海浪波倾角，αc为鳍角。

将式（3）代入式（1），并对代入后的式子进行无量纲化处理，得：

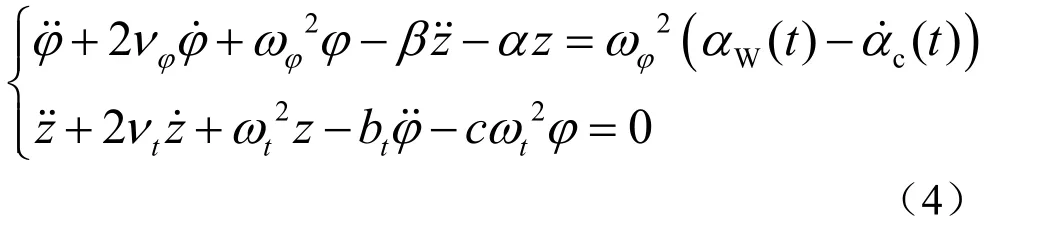
式中：

2 联合控制系统控制方案设计

通过建立数学模型，由式（4）可得到联合系统的模型，如图1所示。其中，减摇鳍采用按横摇角度、角速度和角加速度三者加和的“力矩控制”。船舶/水舱系统分为船舶和被动式水舱两个系统，被动式水舱采用可控的方式进行减摇。

图1 船舶减摇鳍/水舱联合控制系统模型

2.1 减摇鳍控制方案分析与设计

为达到较好的减摇效果，减摇鳍通常采用按横摇角φ、横摇角速度φ˙和横摇角加速度φ˙综合的“对抗控制”，其产生的稳定力矩可由下列关系式确定：

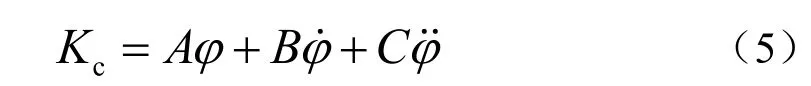
当采用PID控制时，参数 A、B、C 可表示为：

式中，Kh为航速调节系数，KP、KI、KD为 PID参数， lf为减摇鳍上水动力压力中心到船舶重心的作用力臂，ρt为海水密度，V为航速，AF为减摇鳍的投影面积， ∂ Cy/∂α为升力系数斜率。

将式（6）代入式（1），并整理成式（4）的形式，则式（4）中有关(Il+Jt)的式子将改变：

其它不变。当A、B、C满足下式：

则按对抗控制时PID控制器的特点为：

当F、船型以及减摇鳍的参数确定后，为使得等式满足，当船舶航速改变时，PID参数也实时改变，分别为：

可见，当减摇鳍按力矩控制时，不同航速、海况对应不同PID参数。常规PID控制器只能在某个具体工况时使控制效果最好，不能保证任意工作范围内最优。为取得良好的减摇效果，必须引入变参数的 PID。

2.2 减摇水舱控制方案分析与设计

由图1可知，减摇水舱是一个独立的整体，分为船舶和被动式减摇水舱两部分。简单的被动式减摇水舱并不能使船舶在航行时始终保持在比较好的减摇状态下，它会因为海浪干扰的差异而改变。当航行遇到高频干扰时，由于船舶和水舱内的液体本身都具备的比较大的惯性，所以它们对于来自高频海浪干扰所产生的响应不太明显；然而当船舶遭遇低频海浪干扰时，被动式水舱经常会对本来需要减摇的船舶产生比较大的增摇效果。如果仅加入无控制的被动式减摇水舱，不能达到期望的减摇效果。所以，对减摇水舱我们应考虑如何对其施加适当的控制作用，从而可以使水舱内液体振荡的周期和船舶的横摇固有周期相一致协调，控制水舱内液体的液位使船舶的横摇状态保持在可以对船舶横摇运动产生有效减摇效果的相位关系。

设计采用“气阀开关控制式减摇水舱”，由于水舱内的液体在流动的过程中，会产生气体压力差，这种压力差进而会对水舱内的液体做功。打开气阀时，该水舱就相当于完全被动式减摇水舱，水舱两边舷的气体是自由运动的，气体的压缩性对液体运动产生的影响近似为零。如图2所示。

图2 气阀开关控制式减摇水舱

当边舱气阀控制时，气阀和液体表面之间的空气将随边舱内水柱的振荡而产生膨胀或压缩，这一过程可看作多变压缩过程。设气阀关闭时，水舱内水位的相对位移h=h0，下标1、2分别代表左舷边舱和右舷边舱，则左舷边舱内气体状态由多变过程的气体状态方程可得：

式中：P1为气阀关闭时刻左边舱内气体压力，P′1为任意时刻左边舱内气体压力，V1为气阀关闭时左边舱液面上方气体体积，V′1为任意时刻左边舱液面上方气体体积。

则左边舱气阀关闭后气体压强变化量为：

同理，右边舱气阀关闭后气体压强变化量为：

式中，γ为多变压缩过程指数。如果是等温过程，取1；如果是绝热过程，取1.4。则气阀关闭后两边舱之间由于气体膨胀压缩产生的压强差为：

设χ为阀门控制函数，当阀门关闭时，1χ=；当阀门打开时，0χ=。则气阀开关控制式减摇水舱的数学模型：

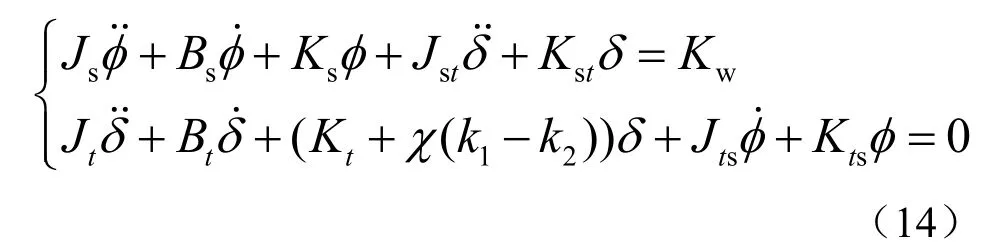
对水舱气阀开关的控制方法采用“以水舱流体速度为反馈信号的闭环控制”，即：将水舱底部连通道水的流动方向作为控制输入，当舱内液体的流动方向改变时，即流过水舱底部连通道的液体速度过零时，控制信号控制气阀使其关闭；当船舶的横摇运动向一侧运动达到最大的横摇角度时，即流过水舱底部连通道的液体速度为零时，控制信号控制气阀使其开启。其控制方法时序图如图3所示。

图3 气阀开关控制

2.3 减摇鳍/水舱联合控制方案分析与设计

综合以上设计分析，联合系统的控制方案设计如下：对减摇鳍采用“变参数 PID的力矩控制”，对减摇水舱采用“以水舱流体速度为反馈信号的闭环控制”。二者联合控制，实现船舶在全航速下有效地减摇。

3 仿真分析

以某船为模型，其参数为：正常排水量为2 320 t；初稳心高为1.438 m；正常排水量下横摇周期为9.140 s；船舶总长为86 m；型宽为13.6 m；型深（至主甲板）为6.2 m；结构方形系数为0.523。设计水舱的参数见表1（a）、（b）。

表1 (a)减摇水舱尺寸

表1 (b)减摇水舱尺寸

减摇鳍采用一对可收放式NACA型减摇鳍。对于减摇鳍的控制器的 PID参数采用粒子群算法的PID参数寻优。PSO算法的方案选取如下：初始化种群规模为N=20，确定表征粒子的维数j=3，加速因子 c1=c2=2，惯性权重 W=0.8，最大迭代次数Kmax=110，参数搜索空间为KP∈[0.1,40]，KI∈[0.1,40]，KD∈[0.1,40]。通过寻优，得到 PID 参数整定结果为：KP=19.8，KI=1.47，KD=11.6。

为验证“系统”控制方案的有效性和优越性，分别对无减摇装置、单独减摇鳍减摇、鳍/水舱联合控制系统在不同海况下进行了仿真，并对仿真结果进行了统计。

图4～图6为有义波高4 m、航速18 kn、遭遇角90°的海况下时的船舶横摇状况。

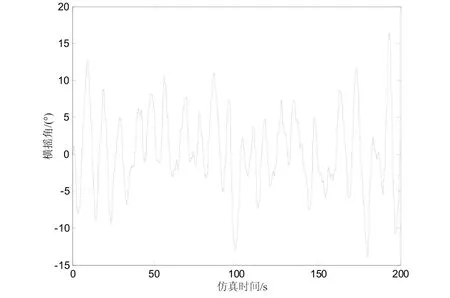
图4 船舶无减摇装置系统

图5 船舶单独减摇鳍控制系统

图6 船舶减摇鳍/水舱联合控制系统

图7～图9为有义波高4 m、航速6 kn、遭遇角90°的海况下的船舶横摇状况。

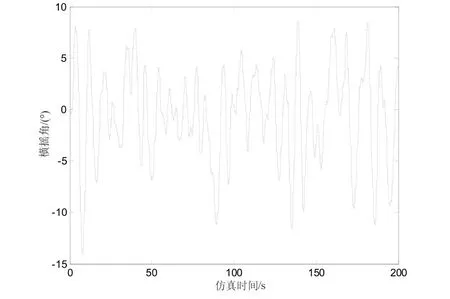
图7 船舶无减摇装置系统

图8 船舶单独减摇鳍控制系统

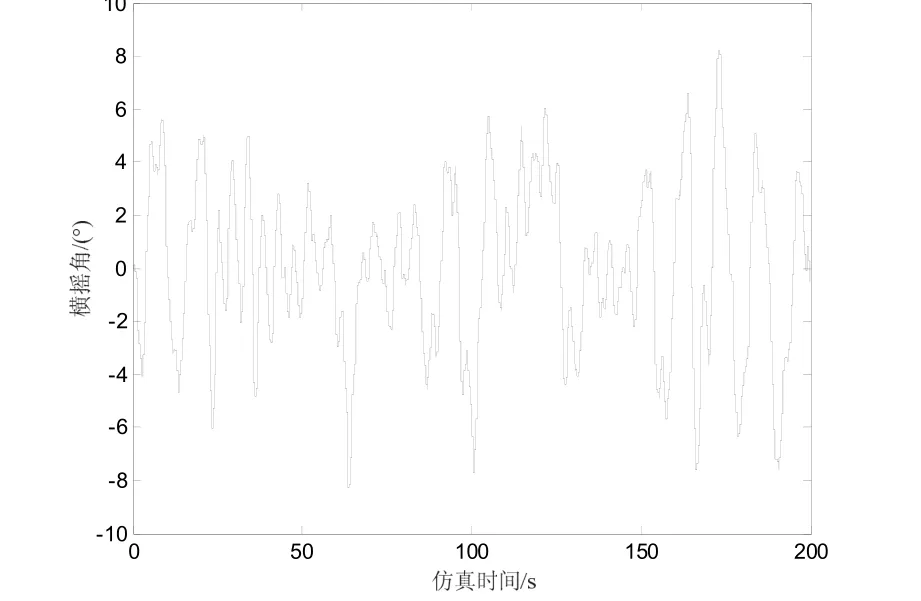
图9 船舶减摇鳍/水舱联合控制系统

图9～图12为有义波高4 m、航速10 kn、遭遇角90°的海况下船舶横摇状况。

图10 船舶无减摇装置系统

图11 船舶单独减摇鳍控制系统

图12 船舶减摇鳍/水舱联合控制系统

对有义波高4 m、船舶航速10 kn、不同遭遇角时，船舶横摇角的均值E(φ)和方差STD(φ)的统计结果如表2、表3。由表中数据可知，在任何遭遇角度下，鳍/水舱联合控制系统和船舶单独减摇鳍控制系统都可以减横摇。单独减摇鳍控制系统的减摇效率很低，特别是在遭遇角为90°时，减摇鳍的减摇效率仅达 23.8%。而鳍/水舱联合控制系统的减摇效率仍可以达到45.8%，比单独减摇鳍减摇提高了22%。

表2 横摇角均值的统计结果

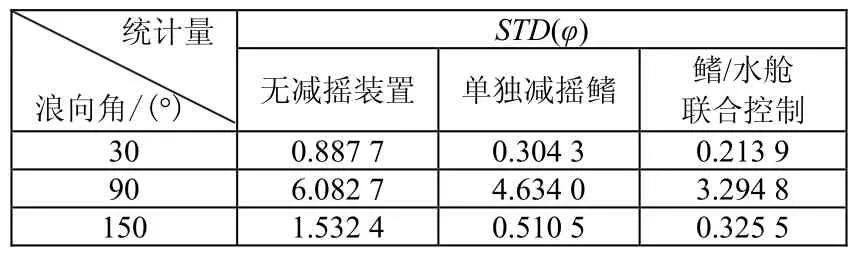
表3 横摇角方差的统计结果

对有义波高4 m、船舶航速18 kn、不同遭遇角时，船舶横摇角的均值E(φ)和方差STD(φ)的统计结果如表4～5。由表中数据可知，在任何遭遇角度下，鳍/水舱联合控制系统的减摇效果均达到70%以上，这是单独的减摇鳍或者单独减摇水舱控制系统无法达到的。

表4 横摇角均值的统计结果

表5 横摇角方差的统计结果

对有义波高4 m、船舶航速6 kn、不同遭遇角时，船舶横摇角的均值E(φ)和方差STD(φ)的统计结果如表6～7。由表中数据可知，单独减摇鳍控制系统和船舶无减摇装置系统的横摇状况基本一致，也就是说，此时减摇鳍并不能起到减摇的作用。而鳍/水舱联合控制系统的减摇效率可以达到 31.1%以上，起到了很好的减摇作用。

表6 横摇角均值的统计结果

表7 横摇角方差的统计结果

4 结论

通过对船舶鳍/水舱联合控制系统进行方案设计和仿真分析，可知：联合控制系统实现了全航速下的有效减摇。尤其在低航速下，加入可控被动式减摇水舱的鳍/水舱联合控制系统解决了以往水舱不加控制的鳍/水舱联合控制系统减摇效率低下的问题。为联合减横摇控制技术提供了新的思路，也为其实际应用提供了理论依据。

参考文献：

[1]金鸿章, 赵为平, 綦志刚, 等. 大型船舶综合减摇系统研究[J]. 中国造船, 2005, 46(1)： 29-35.

[2]金鸿, 姚绪梁. 船舶控制原理[M]. 哈尔滨： 哈尔滨工程大学出版社, 2001：146-47.

[3]马洁, 陈智勇,侯忠生.大型舰船综合减摇系统无模型自适应控制[J]. 控制理论与应用, 2009,11(11)： 1290-1292.

[4]赵为平, 金鸿章, 张海鹏,等. 鳍/被动水舱联合减摇理论研究[J]. 中国造船, 2004, 45(3)： 84-88.

[5]于立君, 金鸿章, 王辉, 等. 减摇鳍-减摇水舱综合减摇实验装置的研究[J]. 海军工程大学学报, 2007,19(2)：25-35.

[6]金鸿章, 赵为平, 綦志刚, 等. 基于遗传算法的减摇鳍-被动式减摇水舱综合平衡系统最优控制器研究[J]. 中国航海,2004, 60(3)： 6-11.

[7]洪超, 陈莹霞. 船舶减摇技术现状及发展趋势[J]. 船舶工程, 2012,34(S2)：236-298.

[8]宋芳. 船舶减摇进入智能时代[J]. 中国船检，2015,(5)：96-97.

[9]宋吉广,梁丽华,金鸿章,等. 零航速减摇鳍自适应主从控制器设计[J]. 控制理论与应用, 2015,(5)：703-708.

[10] LUO WEILIN, HU BINGBING, YU HONGSHAN, et al.Neural network based fin control for ship roll stabilization with guaranteed robustness[J]. Neurocomputing, 2017, 230：210-218.

[11] LUIS CERCOS-PITA JOSE, BULIAN GABRIELE,PEREZ-ROJAS LUIS, et al. Coupled simulation of nonlinear ship motions and a free surface tank[J].Ocean Engineering,2016,120：281-288.

[12] YU LIJUN, DONG ZEQUAN, WANG HUI. The application of dual neural network for control system of four stabilizer fins of ship anti-rolling[C]. 2016 IEEE International Conference on Mechatronics and Automation,2016：2413-2418.

[13] LIU SHENG, SONG YINGHUI. Fin/flap fin anti-roll control for ship based on MSA-PSO intelligent allocation[C].2014 33RD Chinese Control Conference(CCC), 2014：8607-8611.

[14]吴春梅.现代智能优化算法的研究综述[J].科技信息,2012, (8)：31-33.

[15]康琦, 汪镭, 安静,等. 群体智能计算[J]. 上海大学学报(自然科学版), 2004,10(z1)：73-76.

[16]李婷. 基于双种群的改进粒子群优化算法研究[D]. 中南大学, 2007.

[17]朱小明, 张慧斌. PSO算法的稳定性分析及算法改进[J].计算机科学, 2013, (3)：275-278.

[18]刘娇. 改进PSO算法在主汽温系统PID参数优化中的应用[J]. 计算机与现代化, 2009, (12)：29.

[19]汤伟, 袁志敏, 杨鹏飞, 等. 基于 PSO算法的 PID控制器参数优化及其在置换蒸煮立锅温差控制中的应用[J].中国造纸学报,2016,31(4)：39-43.

[20]唐俊. PSO算法原理及应用[J].计算机技术与发展, 2010,(2)：213-216.

[21]姜长元, 赵曙光, 沈士根,等. 惯性权重正弦调整的粒子群算法[J].计算机工程与应用, 2012,48(8)：40-42.

[22] MEHDI MEHDINEJAD, BEHNAM MOHAMMADIIVATLOO, REZA DADASHZADEH-BONAB, et al. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms[J]. International Journal of Electrical Power & Energy Systems, 2016,39(3)：104-116.

[23] YONG ZHANG, DUN-WEI GONG, XIAO-YAN SUN, el al. Adaptive bare-bones particle swarm optimization algorithm and its convergence analysis[J].Soft computing, 2014,18(7)：1337-1352.

[24] MARINAKIS YANNIS, MIGDALAS ATHANASIOS,SIFALERAS ANGELO. A hybrid particle swarm optimizationvariable neighborhood search algorithm for constrained shortest path problems[J]. European Journal of Operational Research, 2017, 261(3)：819-834.

[25]刘志雄, 梁华. 粒子群算法中随机数参数的设置与实验分析[J]. 控制理论与应用,2010,(11)：1489-1496.

[26]王东风, 孟丽, 赵文杰. 基于自适应搜索中心的骨干粒子群算法[J]. 计算机学报,2016,(12)：2652-2667.