考虑既有地下连续墙影响的地铁车站外墙优化设计
2018-04-27雨周钢蒋俊杰
王 雨周 钢蒋俊杰
(1.北京市建筑设计研究院有限公司,100045,北京;2.Thornton Tomasetti Inc.,100004,北京∥第一作者,工程师)
在民用建筑领域,将基坑围护结构与主体地下结构相结合的“桩墙合一”、“两墙合一”技术已得到了初步应用并获得了良好效果[1]。在地铁车站结构设计中,通常直接建立土与结构相互作用的荷载-结构模型进行包络设计,忽略地下连续墙等围护结构的作用,而仅将其作为安全储备。
随着地铁的发展,换乘车站越来越多,明挖基坑的开挖深度也相应增加。地下连续墙结构因工程施工对环境影响小,刚度大、整体性好、安全性高、支护结构变形较小,及抗渗性能良好等优点,被越来越多地用作车站主体基坑的围护结构[2]。由于基坑开挖深度越来越大,为保证基坑本体安全,也为满足对周边环境变形的控制要求,地下连续墙的厚度逐渐增加(一般为 800 mm、1 000 mm、1 200 mm),混凝土强度等级也逐渐提高(现多采用C30、C35等)。
当地下连续墙刚度较大按永久结构设计时,应考虑正常使用阶段地下连续墙与主体结构外墙的共同作用,可对地铁车站主体结构进行优化。这样的设计可有效提高材料利用率,减少相应主体结构投资,节约资源。
1 案例车站工程概况
现以北京某地下三层岛式换乘车站为例进行优化分析。案例车站为双柱三跨混凝土结构,其施工方法采用明挖。有效站台中心处车站顶板覆土厚度为4.47 m,底板埋深约为26.87 m。标准段总宽23.10 m,总高22.40 m;车站总长185.25 m,岛式站台宽度为14.00 m,有效站台长118.00 m。车站主体结构采用C40混凝土,HRB 400级钢筋。
明挖基坑标准段开挖深度约为27.07 m,盾构段开挖深度约为27.98 m。开挖深度内土层主要有第②层粉质黏土,第②2层粉土,第③4层中细砂,第③6层卵石,第④层粉质黏土,第④2层粉土,第④3层粉细砂,第⑤层卵石,第⑤2层中细砂,第⑤4层粉质黏土。基底位于第⑥层粉质黏土及第⑥2层粉土中。
车站基坑工程采用800 mm厚地下连续墙围护结构+内支撑的围护形式。内支撑采用钢支撑,共设置5道钢支撑及+1道倒撑。地下连续墙采用抗渗等级为P8的C35水下混凝土及HRB400级钢筋。
车站3层主体结构原设计均采用800 mm厚C40混凝土外墙。现将既有地下连续墙与车站外墙“水平向结合”“两墙合一”,使地下连续墙与车站外墙成为共同受力体系。在近期正常使用阶段,静止土压力和水压力直接作用于地下连续墙;在远期正常使用阶段,水压力作用于车站外墙结构,静止土压力作用于地下连续墙,并通过地下连续墙-车站外墙体系传递给车站地下室外墙。
经分析,抗震组合荷载不起控制作用,故优化设计中按承载力使用极限状态、正常使用极限状态及人防荷载组合状态等3种情况进行包络。地面超载及人防荷载中的水平荷载作用于地下连续墙,竖向荷载作用于车站结构顶板及底板。
2 仿真模拟
本文采用SAP2000软件建立了包含地下连续墙及车站结构的板墙二维有限元模型。其中,框架柱按等刚度原则折算为每延米的杆件,在顶板两侧根据抗浮验算设置结构压顶;车站结构与地下连续墙及压顶之间采用只压型刚性链杆连接;以GAP单元模拟土弹簧作用,以LINEAR单元模拟地下连续墙及车站外墙间的相互作用。考虑地下连续墙及不考虑地下连续墙的计算模型分别如图1及图2所示。按是否考虑地下连续墙刚度进行优化设计,分析了地下连续墙刚度对车站外墙内力及配筋率的影响,并对车站结构进行优化设计。
图1 考虑地下连续墙的计算模型
图2 不考虑地下连续墙的计算模型
2.1 地下连续墙刚度对车站外墙内力的影响
为分析地下连续墙对车站外墙内力的影响,按车站外墙厚度分别为600 mm、700 mm、800 mm及900 mm等4种情况,分析顶板、2层中板及底板的墙支座(边跨支座)、梁支座(中跨支座)、边跨跨中及中跨跨中,以及3层外墙的上端支座、跨中及下端支座等几个控制界面。由于正常使用极限状态与承载力极限状态下的内力存在相关性,故内力影响分析只考虑承载力极限状态(以下简称“基本组合”)和人防荷载组合状态(以下简称“人防组合”)的弯矩。
未考虑地下连续墙刚度的外墙弯矩为M0,考虑地下连续墙刚度后的外墙弯矩为M0+ΔM,则弯矩变化率(ΔM/M0)如图3所示。由图3可见,弯矩变化率有如下特点:
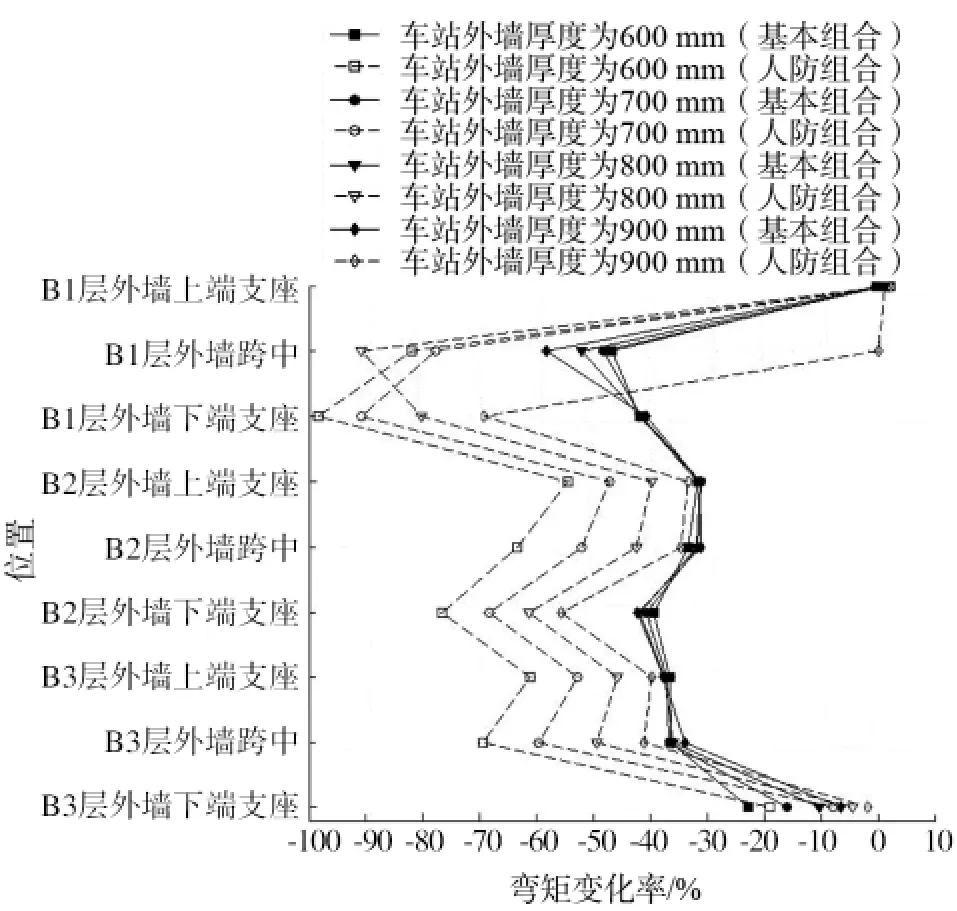
图3 外墙弯矩变化率
(1)在顶板支座处,在不同墙厚、不同工况中外墙弯矩变化率并未显著减小,反而有小幅度(约2%)的增加,且人防组合的弯矩增加较基本组合更明显。
(2)在顶板支座处,基本组合的外墙弯矩增长率随墙厚增加而增加,人防组合的外墙弯矩增长率随墙厚增加而减小。
(3)在底板支座处,外墙弯矩有一定幅度的减小,基本组合的外墙弯矩变化率高于人防组合,且变化率随外墙厚度增加而减小。
(4)其他位置的外墙弯矩减小幅度显著高于顶板及底板支座处。
(5)在顶板及底板支座处,人防组合的外墙弯矩变化率小于基本组合;在其他位置,基本组合的外墙弯矩变化率小于人防组合。
顶板及底板的弯矩变化率(如图4所示)有以下特点:
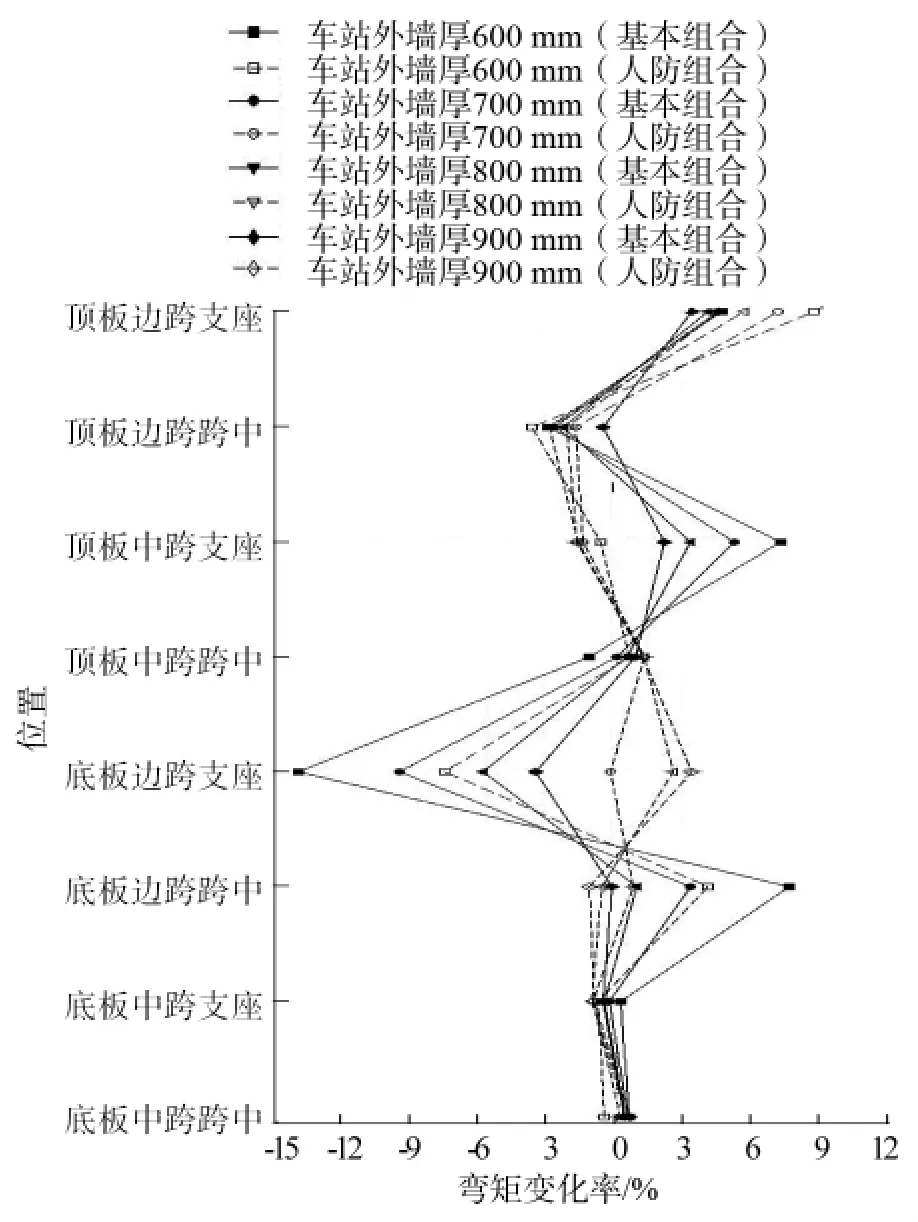
图4 顶板及底板弯矩变化率
(1)由于地下连续墙的作用,顶板墙支座处弯矩不降反升,且人防组合的弯矩变化率大于基本组合,与外墙顶板支座处变化规律一致。
(2)在人防组合与基本组合中,顶板墙支座处弯矩变化率均随墙厚增加而减小。
(3)在基本组合下,底板墙支座处的弯矩均有一定幅度减小,且弯矩变化率均随墙厚增加而减小;在人防组合下除600 mm厚的外墙外,其他外墙的弯矩均小幅增加。
(4)在考虑了地下连续墙刚度影响后,顶板中跨支座及底板边跨跨中处的弯矩增加,且增加幅度随结构厚度的增加而减小。
(5)地下连续墙刚度对顶板边跨跨中、顶板中跨跨中、底板中跨支座及顶板中跨跨中等处弯矩的影响较小。
由于地下连续墙刚度的影响,中板弯矩变化率(如图5所示)有以下特点:
(1)B1层边跨支座在基本组合及人防组合组合下,弯矩均呈现减小,且变化率随外墙厚度增加而减小。
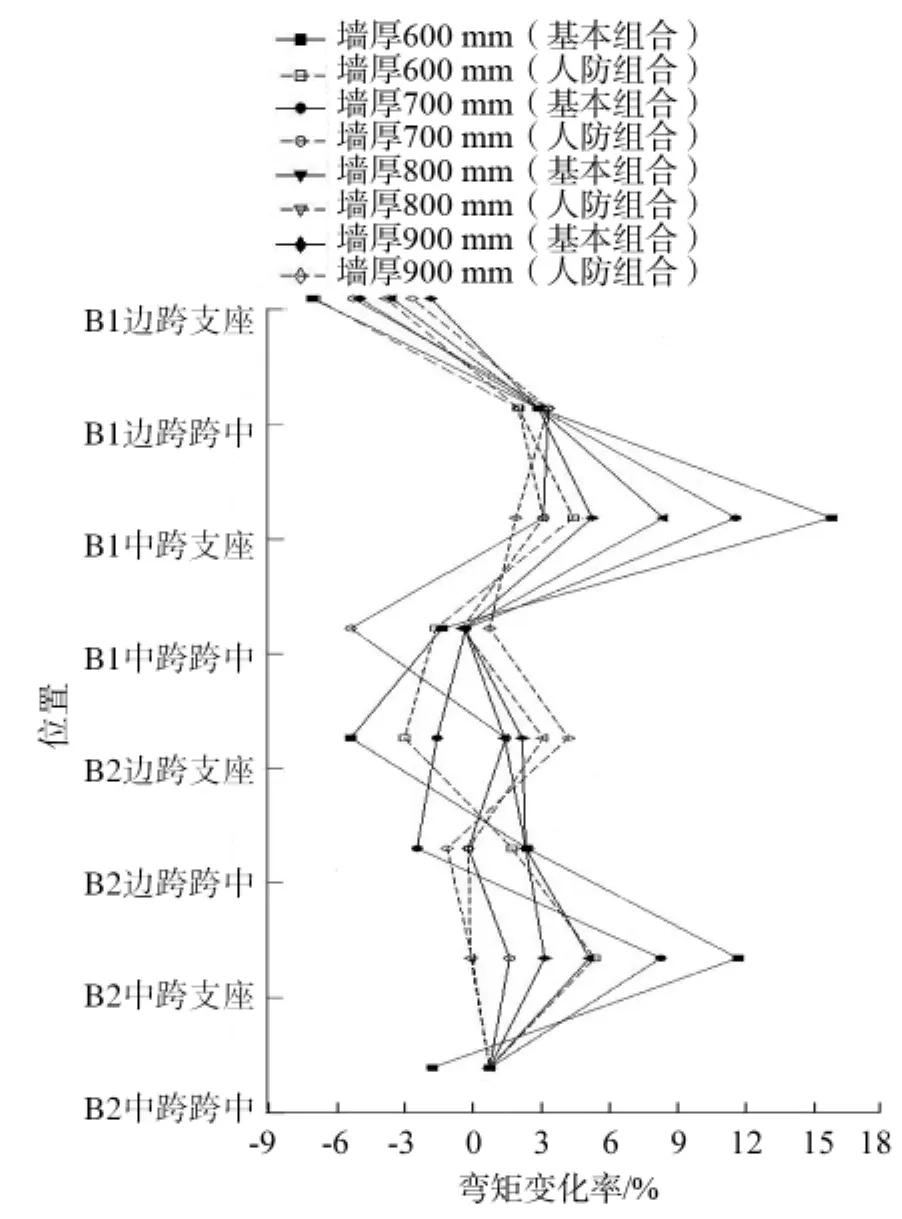
图5 中板弯矩变化率
(2)B2层中跨跨中处的弯矩变化很小,可忽略。
(3)B1层与B2层中板其他位置的弯矩均有增大的可能。
2.2 地下连续墙刚度对车站配筋率的影响
在车站外墙的配筋设计中,正常使用极限状况按迎土面结构裂缝不大于0.2 mm、背土面结构裂缝不大于0.3 mm的要求来控制。
当以裂缝控制作为配筋设计考虑因素时,随着埋深加大,各层外墙受到的水平侧力差别也增大,从而导致外墙各处弯、压状态程度不同。因此,应将外墙分别按纯弯构件和压弯构件两种情况考虑。
当车站外墙按纯弯构件计算时,如考虑地下连续墙刚度的影响,则车站外墙配筋率变化(见图6)呈如下特点:
(1)顶板与底板支座处的配筋率变化较小,对墙厚仍起控制作用。
(2)当外墙厚度与地下连续墙厚度(800 mm)接近时,顶板支座处的配筋率呈小幅上升。
(3)B1层跨中处弯矩本来就较小,因此在地下连续墙刚度影响下虽该处弯矩大幅减小,也仍按照最小配筋率配筋,其配筋率变化为0。
(4)车站外墙厚度越大,地下连续墙对实际配筋率的优化影响越小。
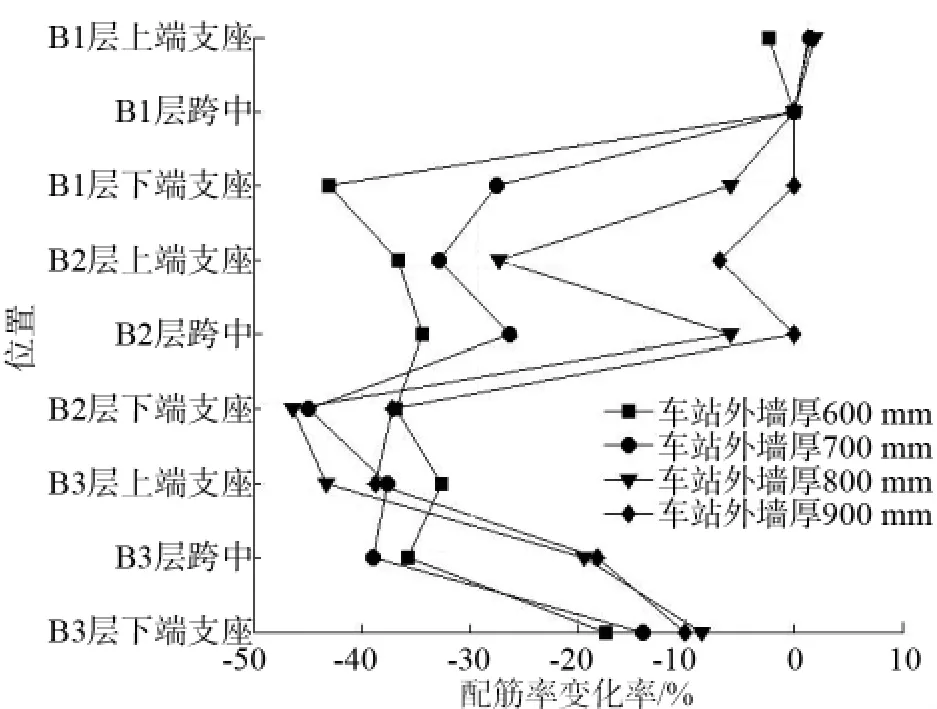
图6 外墙按纯弯构件计算的配筋率变化
(5)除顶板与底板支座处,考虑地下连续墙刚度后,车站外墙在迎土面的配筋率减小大于背土面一侧。
当车站外墙按照压弯构件计算时,考虑地下连续墙刚度的影响,车站外墙的实际配筋率变化(见表1)呈如下特点:
(1)地下连续墙刚度的变化趋势与纯弯构件配筋率的变化趋势基本一致,考虑压力的有利影响时,能更大幅地降低墙体配筋率。
(2)原设计中800 mm厚外墙按照压弯构件考虑时,B1层及B2层大多数位置可按照最小配筋率配筋。而在考虑地下连续墙影响后B2层下端支座处配筋率降低很多。由此说明了B1层与B2层外墙截面优化的必要性。
考虑地下连续墙刚度影响,顶板与底板配筋率变化(见图7)有如下特点:
(1)外墙厚度不同时,顶板边跨支座及中跨支座处的实际配筋率均出现了小幅上升。
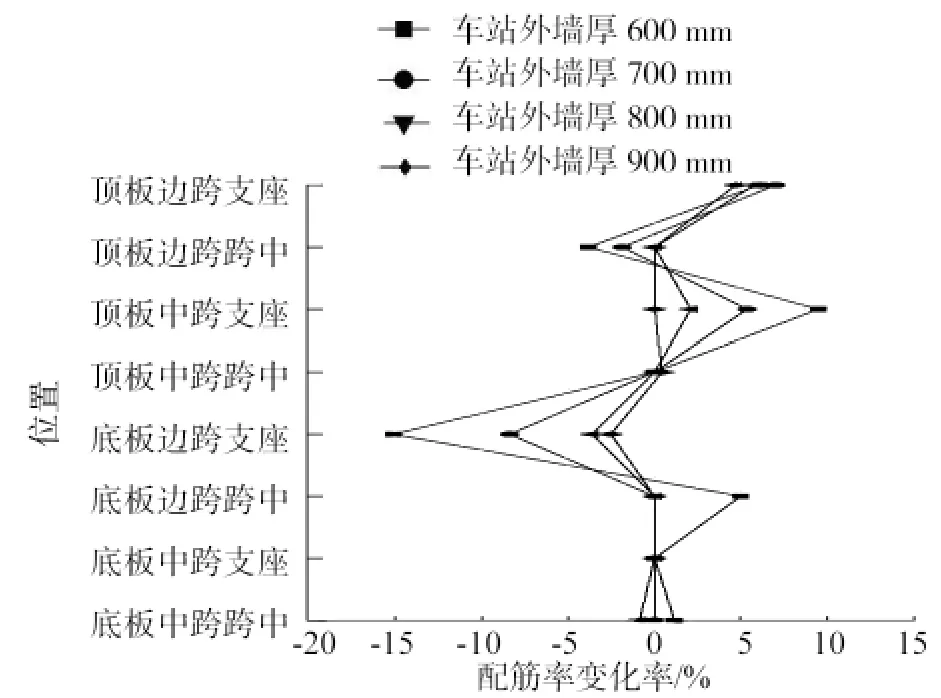
图7 顶板与底板配筋率变化
(2)底板边跨支座处的配筋率有所降低,且外墙厚度越小,配筋率降低幅度越大。
(3)地下连续墙刚度对顶板及底板其他位置的实际配筋率影响不大。
B2层中板配筋率变化(见表2)有如下特点:

表2 外墙厚度不同时的B1、B2层中板配筋率变化率
(1)B1层及B2层中板边跨支座配筋率均有降低。
(2)B2层中板支座配筋率在不同外墙厚度情况下均有所增加。
(3)地下连续墙对中板其他位置的配筋率基本没有影响。
2.3 外墙优化设计
车站外墙的外侧支座为配筋控制截面。B3层外墙下端支座处配筋率最高。墙厚不同时,考虑地下连续墙刚度影响的实际配筋率见表3。车站外墙厚900 mm的方案经济性差且配筋变化率小;墙厚600 mm及700 mm方案虽配筋率变化较大,但标准断面配筋率仍偏大。根据一般规律,侧墙一侧或两侧开洞后,侧墙弯矩及配筋都高于标准断面。因此,B3层外墙可选择800 mm厚度。
为施工方便,车站B1及B2层外墙选择同一厚度,外墙厚600 mm及700 mm时的配筋率均符合要求。但由于B3层与B2层外墙支座处钢筋拉通,故600 mm厚外墙配筋率略大,且与800 mm厚B3层外墙衔接时的刚度突变较多,故B1层及B2层选择700 mm厚外墙。
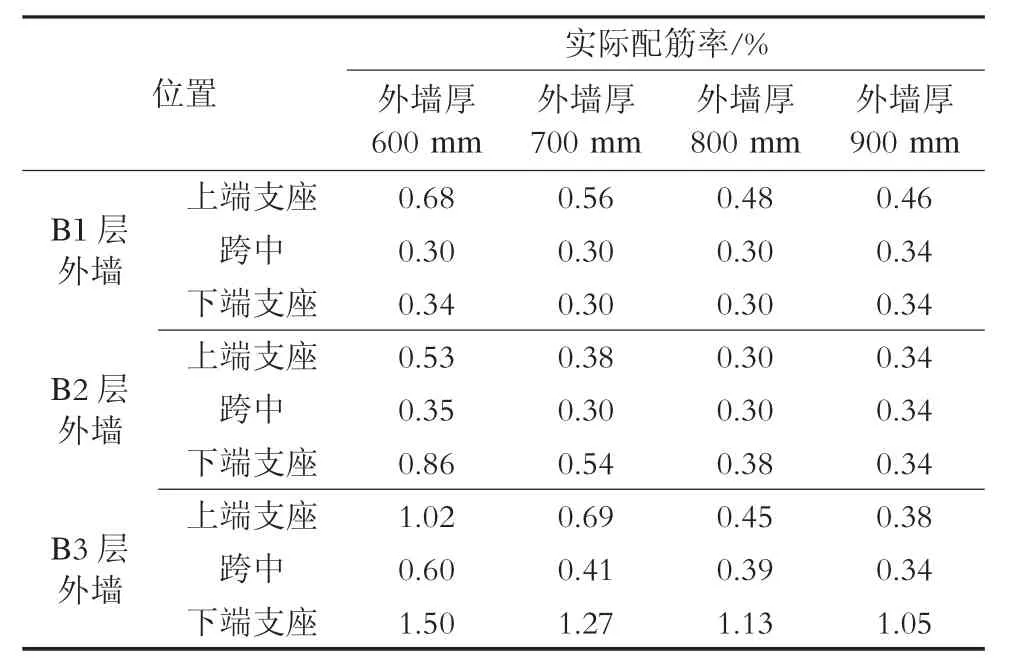
表3 考虑地下连续墙刚度后各墙厚实际配筋率
3 结论
(1)在考虑地下连续墙刚度时,应建立完整的地下连续墙与地下主体结构共同作用的模型。直接折减外墙荷载算法的结果偏差较大。
(2)计算中如考虑地下连续墙刚度,则对外墙的内力和配筋有一定幅度的优化,对B1层和B2层的内力及配筋减小幅度比B3层的大,且优化幅度随外墙厚减小而增加。
(3)当以裂缝控制作为配筋设计考虑因素时,既有地下连续墙的影响规律在假定外墙为纯弯构件和压弯构件时基本一致。外墙作为压弯构件分析时,墙体配筋率更小。
(4)地铁车站外墙作为纯弯构件分析时,地下连续墙对外墙的顶板支座影响很小,考虑地下连续墙刚度时的顶板、中板和底板部分位置的内力及实际配筋比不考虑地下连续墙刚度时有一定增加。可见,地下连续墙不能全面优化整个结构所有位置的内力及实际配筋。
(5)假定外墙为压弯构件时,考虑地下连续墙刚度可整体优化各层外墙的实际配筋,且随墙厚减小,优化作用越明显。
(6)考虑地下连续墙刚度影响时,顶板、中板和底板部分位置的内力及实际配筋比不考虑地下连续墙刚度影响时有一定幅度的增加。因此地下连续墙不能全面优化整个结构所有位置的内力及实际配筋。
(7)由于地下连续墙刚度影响的实际存在,顶板、中板及底板的配筋设计不宜过低。
[1] 胡耘,王卫东,沈健.“桩墙合一”结构体系的受力实测与分析[J].岩土工程学报,2015,37(S2):197.
[2] 刘国彬,王卫东.基坑工程手册[M].2版.北京:中国建筑工业出版社,2009.
[3] 王雨,刘国彬,屠传豹.基于遗传-GRNN在深基坑地下连续墙测斜预测中的研究[J].岩土工程学报,2012(S1):167.
