纳米孔单分子传感器电导特性有限元分析*

伍根生， 张泓伟， 于 波， 马冬琴， 宋福磊

(南京林业大学 机械电子工程学院，江苏 南京 210037)

0 引 言

常见的纳米孔[1,2]材料有氮化硅、氧化硅以及最近热门研究的一些二维材料如石墨烯[3～5]、二硫化钼[6]、氮化硼[7]等。根据目前的微机电系统工艺，氮化硅可以加工最薄至20 nm左右，但石墨烯以及一些二维材料的厚度往往在1 nm以下，10层石墨烯厚度也只有3.4 nm左右。运用二维材料加工纳米孔的主要原因是考虑到DNA分子上各个碱基的距离与二维材料的厚度接近，这样有便于DNA碱基序列检测。而实验研究表明，厚度的降低并不能有效地提高纳米孔识别生物分子的精度[3,4]。模拟研究也表明三层石墨烯纳米孔的分辨率比单层以及五层的高[8]。另外，生物纳米孔相关实验研究表明其分辨率比一般固态纳米孔的要高[9～11]。如果从结构上来看，生物纳米孔除了有比较窄的纳米孔区域，还有一段孔径较大的区域。而石墨烯纳米孔在转移过程中，一般是用2 μm的氮化硅纳米孔作为衬底。为了让固态纳米孔的结构与生物纳米孔的结构接近，可使得氮化硅衬底的直径进一步减小到20 nm左右。这样来模拟生物孔结构，便于分析其分辨率。

本文模拟了常见的两种纳米孔结构，以及一种仿生纳米孔结构。通过模拟的结果比较下不同纳米孔对于检测纳米杆以及纳米杆上带有亚结构的相对电流堵塞值。

1 模型验证

纳米孔的电导主要由2部分组成，孔内电阻和接入电阻值[12]，如图1(a)所示。随着纳米孔的厚度逐渐降低，接入电阻值逐渐占主导地位，比如超薄纳米孔中基本只考虑接入电阻值的影响[5]，如图1(b)所示。模拟生物纳米孔的结构，可得到图1(c)所示的两层纳米孔结构。

常用的模拟纳流体离子输运的模型主要有两种，在文献[13]中有详细的讨论，本文采用Nernst-Plank，Possion以及Navier-Stokes方程组成的NP模型。相应地，在COMSOL有限元模拟中考虑了在1mol/L氯化钾(KCl)溶液中离子迁移相关的3个物理场，分别为静电场、稀物质传递、N-S方程。模拟开始以纳米孔A为例，验证所建立的有限元模拟的有效性，纳米孔A的电导可以理论公式计算直接得到。对于复杂形状纳米孔的电导，采用有限元模拟进行电导计算。纳米孔的电导除了受到孔的几何尺寸影响以外，还与纳米孔壁面电荷相关。本文分别从壁面无电荷和有电荷的角度，来计算纳米孔的电导，验证理论公式的适用条件。

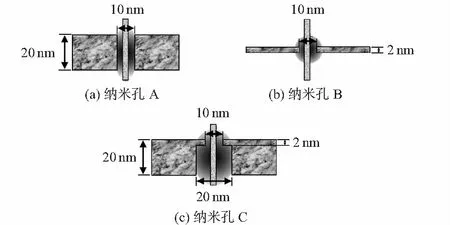
图1 3种不同尺寸结构的纳米孔示意图

1.1 无壁面电荷的纳米孔电导计算

1)根据Kowalczyk描述的纳米孔电导计算公式如下[14]

(1)

式中σ=F(μK+μCl)c为离子溶液电导率[5]，F为法拉第常数(9.649×104C/mol)，μK=7.616×10-8m2/(V/s),μCl=7.909×10-8m2/(V/s)分别为钾离子(K+)和氯离子(Cl-)的离子迁移率[15];l,d分别为纳米孔的厚度与直径，nm。该模型主要考虑了形成纳米孔圆柱部分的电导和接入部分电导，计算结果如图2所示。

2)根据Smeets描述的纳米孔电导计算公式为[15]

(2)

式中σW为壁面电荷密度；e为元电荷；nKCl为KCl溶质的数密度。该公式主要考虑了纳米孔圆柱部分和壁面电荷对电导的影响。

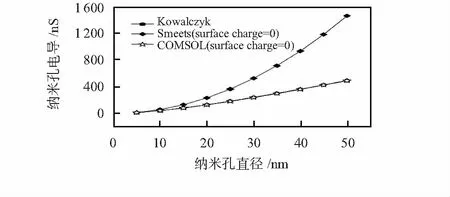
图2 不考虑壁面电荷纳米孔的电导模拟

图2所示为纳米孔孔径在5～50 nm范围内的电导计算，通过式(1)和式(2)的计算以及有限元模拟纳米孔A的结果。在有限元模拟过程中，设置纳米孔壁面电荷密度为0。有限元模拟的结果与Kowalczyk的结果比较接近，因为有限元模拟过程中既考虑纳米孔圆柱部分电阻值，也考虑了接入电阻值的影响。因此，在同一纳米孔直径的条件下，纳米孔电导均较Smeets模型预测的值要低。

1.2 考虑壁面电荷的纳米孔电导计算

大部分的固体物质在盐溶液中均带电，考虑壁面电荷密度后，Kowalczyk模型因不能描述壁面电荷的影响而失效，但Smeets模型又未考虑接入电阻值的影响。本文综合考虑这两个因素，将Smeets模型中加入了接入电阻值的影响也即得到Smeets+Access模型，其表达式为

(3)

假设壁面材料为氮化硅，取壁面电荷密度为σW=-0.012 C/m2[16]，根据式(2)和式(3)计算的结果以及有限元模拟结果对比如图3所示。由图3可见，Smeets+Access模型计算结果与有限元模拟结果基本吻合。

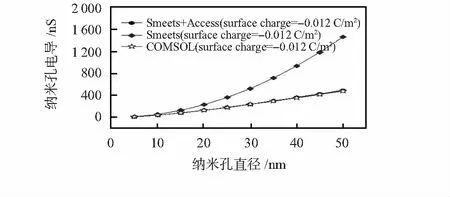
图3 考虑壁面电荷的纳米孔电导模拟

通过以上分析，本文中有限元的模拟设置，可以适用于本文所列出的纳米孔电导模拟，并综合考虑了孔电阻值、接入电阻值和壁面电荷对纳米孔电导的影响。

2 不同纳米孔结构电导计算

模型设置：纳米杆的长度为100 nm，直径为4 nm。纳米杆的壁面电荷密度为-0.076 25 C/m2[16]，纳米孔壁面电荷密度为-0.012 C/m2。为了便于比较，3类纳米孔的最小直径均设为10 nm,如图4。

网格设置：模型采用三角形网格对区域进行划分，最小单元尺寸0.04 nm，最大单元尺寸2.8 nm，网格数控制在4 000～8 000，并对模拟结果做网格相关性检查。

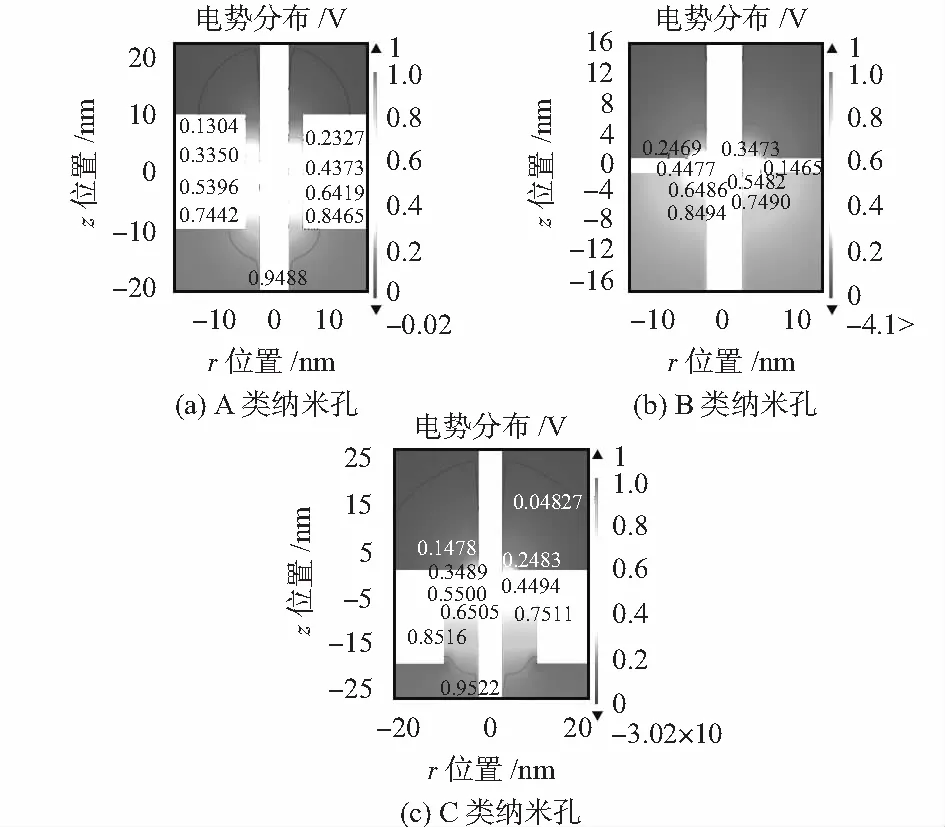
图4 纳米杆位于3类纳米孔结构中的电势分布

2.1 纳米杆堵塞电流计算

图4分析3类纳米孔中存在纳米杆时的电势分布，对于A类和C类纳米孔电势降主要集中在纳米孔内，对于B类纳米孔，由于纳米孔的厚度较薄，电势影响范围更大，约50 nm左右，纳米杆的长度大于其电势影响范围。

为了比较各类纳米孔检测纳米杆的分辨率亦即相对电流堵塞值，首先要计算无纳米杆时的纳米孔电流，在有限元模拟中，纳米孔的离子电流可通过沿着半径方向对电流密度j进行积分计算得到，认为纳米孔内电流密度j在环形微元相同，环形微元的面积为2 πrdr，截面内的电流为

(4)

式中R为纳米孔半径；zi为第i个组分的价态(对于KCl溶液，i=1,2分别代表了K+和Cl-)；Ni为沿着z方向的离子总通量中，在多物理场模拟中可通过耦合求解得到，F为法拉第常数。

运用同样方法计算3类纳米孔内存在纳米杆时的离子电流。并计算各自的相对堵塞电流值，ΔIrod=(I-Irod)/I，计算结果如表1所示。

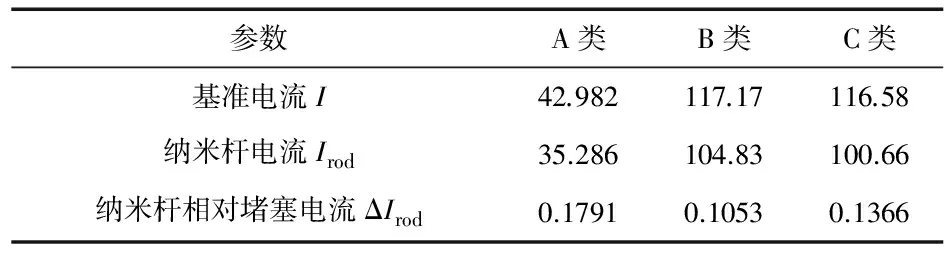
表1 不同纳米孔中纳米杆堵塞电流值 nA

从表1可以看出，对于链状纳米杆，A类纳米孔的电流堵塞值在3种类型纳米孔中最大，为17.91 %，其次为C类纳米孔，B类纳米孔的相对电流堵塞值最小。因为对于B类纳米孔，其接入电阻值占主导地位，由于纳米杆的尺寸与接入电阻值区域相比，实在太小，影响非常有限。

2.2 纳米杆上亚结构的堵塞电流计算

亚结构设置为一半径为2 nm的环状结构。模拟结果如图5所示，由于亚结构的存在，电流堵塞值相应地增大，所以电势降都更集中在纳米孔附近，纳米杆沿着长度方向向外，对纳米孔电势影响越来越小。同样地，计算这三类纳米孔中存在带亚结构的纳米杆时的相对电流堵塞值，依据ΔIsub=(I-Isub)/I，其结果如表2所示。由表中结果可以发现，C类纳米孔的堵塞电流值在三类纳米孔中最大为61.42 %，其次为B类纳米孔，亦即B类纳米孔在检测亚结构方面，较A类纳米孔确有一定的优势。如果将A，B两类纳米孔的特点结合起来，也即C类纳米孔，那么分辨率可以达到更高，从结构特点角度也解释了生物纳米孔比固态纳米孔分辨率高的原因。

3 纳米杆堵塞纳米孔离子电流机理

3类纳米孔在检测纳米杆的对比中，A类纳米孔厚度(长度)较大，对于检测z方向尺寸(l)较大的纳米杆具有更大的优势，B类纳米孔的接入电阻值影响着其主要电导G=σd，检测直径方向尺寸较大的纳米杆具有优势。带有亚结构的纳米杆对纳米孔电导的堵塞分为两个部分：纳米杆自身部分和增大了部分纳米杆的直径。因此C类纳米孔对于检测带亚结构的纳米结构具有更大的优势。

图5 带有亚结构的纳米杆位于不同纳米孔结构中的电势分布

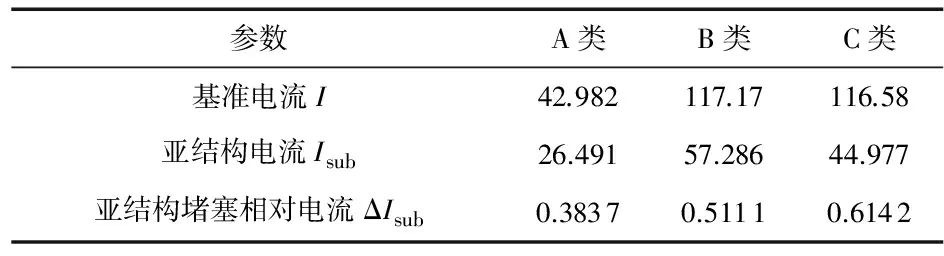
参数A类B类C类基准电流I42．982117．17116．58亚结构电流Isub26．49157．28644．977亚结构堵塞相对电流ΔIsub0．38370．51110．6142

4 结 论

本文主要采用有限元方法模拟了3种不同结构纳米孔的电导特性，从识别链状纳米杆的结果来看，A类常规纳米孔的相对电流堵塞值最大，识别精度最高达到17.91 %。如果检测纳米杆上的亚结构，结果显示C类纳米孔的相对电流堵塞值最大，为61.42 %。从模拟结果也可以看出，对于不同结构的分子，应采用不同结构的纳米孔加以区分。

参考文献:

[1] Zhang X Y,Price N E,Fang X,et al.Characterization of interstrand DNA-DNA cross-links using the alpha-hemolysin protein nanopore[J].AES Nano,2015,9(12):11812-11819.

[2] Merchant C A,Healy K,Wanunu M,et al.DNA translocation through graphene nanopores[J].Nano Letters,2010,10(8):2915-2921.

[3] Schneider G F,Kowalczyk S W,Calado V E,et al.DNA translocation through graphene nanopores[J].Nano Letters,2010,10(8):3163-3167.

[4] Garaj S,Hubbard W,Reina A,et al.Graphene as a subnanometre trans-electrode membrane[J].Nature,2010,467(7312):190-193.

[5] Liu K,Feng J,Kis A,et al.Atomically thin molybdenum disulfide nanopores with high sensitivity for DNA translocation[J].ACS Nano,2014,8(3):2504-2511.

[6] Liu S,Lu B,Zhao Q,et al.Boron nitride nanopores:Highly sensitive DNA single-molecule detectors[J].Advanced Materials,2013,25(33):4549-4554.

[7] Li J,Zhang Y,Yang J,et al.Molecular dynamics study of DNA translocation through graphene nanopores[J].Physical Review E,2013,87(6):062707—1-062707—6.

[8] Borsenberger V,Mitchell N,Howorka S.Chemically labeled nucleotides and oligonucleotides encode DNA for sensing with nanopores[J].Journal of the American Chemical Society,2009,131(22):7530-7531.

[9] Clarke J,Wu H,Jayasinghe L,et al.Continuous base identification for single-molecule nanopore DNA sequencing[J].Nature Nanotechnology,2009,4(4):265-270.

[10] Derrington I M,Butler T Z,Collins M D,et al.Nanopore DNA sequencing with MspA[C]∥Proceedings of the National Academy of Sciences,2010:16060-16065.

[11] Hall J E.Access resistance of a small circular pore[J].The Journal of General Physiology,1975,66(4):531-532.

[12] Liu H,Qian S,Bau H H.The effect of translocating cylindrical particles on the ionic current through a nanopore[J].Biophysical Journal,2007,92(4):1164-1177.

[13] Kowalczyk S W,Grosberg A Y,Rabin Y,et al.Modeling the conductance and DNA blockade of solid-state nanopores[J].Nanotechnology,2011,22(31):315101—1-315101—5.

[14] Smeets R M,Keyser U F,Krapf D,et al.Salt dependence of ion transport and DNA translocation through solid-state nano-pores[J].Nano Letters,2006,6(1):89-95.

[15] Zhang Y,Wu G,Si W,et al.Ionic current modulation from DNA translocation through nanopores under high ionic strength and concentration gradients[J].Nanoscale,2017,9(2):930-939.