基于多元退化数据的航空机电系统竞争故障预测∗

孟 蕾 许爱强 董 超

（1.海军航空工程学院飞行器工程系 烟台 264001）（2.海军航空工程学院科研部 烟台 264001）（3.海军航空工程学院基础部 烟台 264001）

1 引言

航空机电系统发生故障模式有两种，退化故障和突发故障，其最终故障是两种故障模式竞争的结果。目前国内外文献研究竞争故障问题，都是在突发故障与退化故障两者不相连的情况下，着重于从单边退化角度展开论述，是退化量、突发故障单一化的集中体现，退化量的多元化始终未能在学界占主导。对于这样的问题，本文主要是通过航空机电系统提出了退化特性，构建了多元退化量的航空机电系统的竞争和预测模型。

本文中，以最小二乘支持向量机预测法为基本计算工具，简要的对退化参数做了基本测算，如非线性、小样本等；退化量、故障间存在着非常特殊的联系，为寻找隐含性质，引入了“位置-尺度模型”，得出突发故障与退化量的相关参数，进而根据竞争故障预测模型得到了航空机电系统未来一段时间内的竞争故障概率。立足案例，在比较研究之后，认为本文在方法论上具有优势，满足精度要求。

2 构建航空机电系统竞争故障预测模型

假设存在的性能特征参数数量是n，xi(t)、Ui和Li分别代表i(i=1，…，n)个性能特征参数的退化量与上、下阈值。测试起始时间为t，则有G(x，βi)（其中βi=(β1，β2，…，βk)，为该分布的参数向量），对应的概率密度函数g(x，βi) 可表示为

工业部门对故障的概念进行了界定，对性能特征参数的退化量的标准值和阈值范围，有着严格的退化量限制，如果大于了规定的标准，则故障难免。假设第i个性能特征参数在发生了退化故障，则可依据下式计算其可能性：

因为航空机电系统本身就具有n个特定性能的参数，任一参数出现了退化故障，将会导致整个系统会产生故障。所以，可以把系统的故障视为由n个性能特征参数的退化故障通过竞争而产生的。假设所有的性能和特征参数之间保持相对独立，则在t时刻航空机电系统的退化故障的概率可以通过下面的公式进行估算。

突发故障这一指标不但和时刻t等有关联，而且与t时刻某性能特征参数的退化量xi(t) 等指标有关联。在航空机电系统中，若突发故障必然由退化量引起，故障出现时间是Th，且在产生关系的临界时间Th会伴随失效率（λi(t，x)）的同时出现，则Th的可靠性关系式为

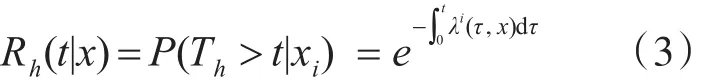
航空机电系统在t时刻的突发故障概率可表示为

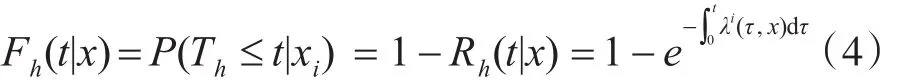
对于竞争故障出现的概率，其算式是

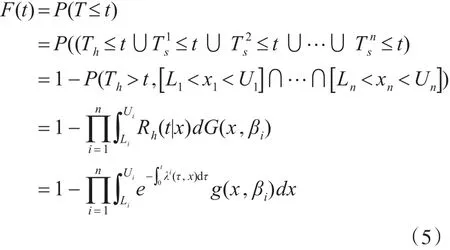
3 航空机电系统竞争故障的预测流程

航空机电系统进行竞争故障预测的具体流程如下：首先确定性能退化参数与突发故障参数的分布类型；然后预测退化的未知参数，确定下一阶段性能退化参数的分布函数；在考虑突发故障与退化量的相关度的情况下，求出突发故障预测模型的未知参数；最后对航空机电系统退化与突发竞争故障概率进行预测。

3.1 分布函数的确定

性能退化参数分布类型的检验，本文采取Копмогоров检验方法。假设其分布函数G(x，β)的分布类型与时间t无关，只是参数向量β随时间t的变化而改变，则G(x，β)即可看作β与时间t的函数，可表示为G(x，β(t))。在确定G(x，β(t))的分布种类前，不妨借鉴工程实践经验，并且针对假设进行分布拟合检验，最终确定出G(x，β(t))的分布类型。综合考虑航空机电系统的双向退化与单边退化。通常情况下，都会将正态分布N(x;μ，σ2)作为理想化选择，相应的密度函数如式（6）所示：

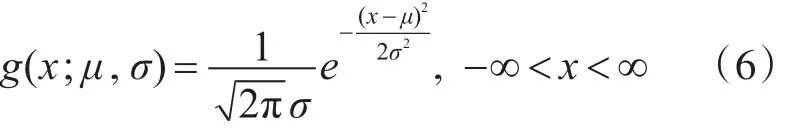
式中，μ和σ2分别表示t时刻性能退化数据的均值和方差，则性能退化数据的分布参数向量β=(μ，σ2)，易知，β与时间t相关。

对航空机电系统性能退化数据分布类型的检验就变为一个正态性检验过程，可利用样本(X1，X2，…，Xn)对总体的分布是否服从N(μ，σ2)进行检验。 样本从小到大排列成：X(1)≤X(2)…≤X(n)。利用式（7）计算统计量W，式中ak(W)的值可查表获得［1］。

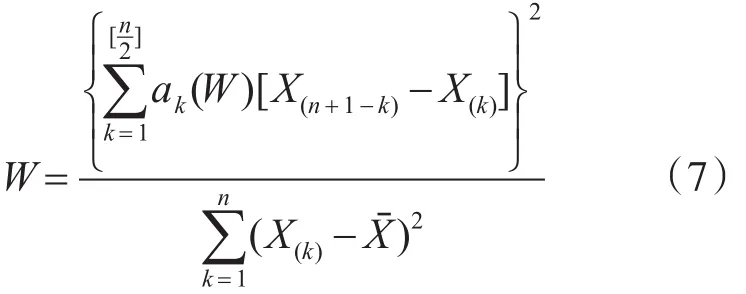
然后在给定显著性水平α与样本容量n下，通过查表可得Wn，α。若W＜Wα，则拒绝H0，否则接受H0。

针对突发故障数据，本文根据工程经验假设其服从威布尔分布。检验方法仍采用Копмогоро对假设的航空机电系统突发故障数据分布类型进行验证，验证过程与性能退化数据分布类型的检验类似。

3.2 参数的预测

3.2.1 退化故障参数预测

3.1节得出性能退化数据的分布类型，从而得出性能退化分布参数。根据历史性能退化数据求解分布参数的历史数据值，求解将来参数，确定分布函数，对退化故障、发生几率做预测。

航空机电系统的性能退化数据的获取主要基于状态监测系统或者是加速退化实验，本文研究的性能退化数据主要是来源于状态监测系统获取的数据。通过测试取得了相应的性能数据是和时间相关的指标，分布参数也将会随着时间的变化而调整。为此，可从时间序列角度审视。根据上文相关论述，可以很清晰得知：从时间序列角度展开预测性能退化故障活动将显得非常的简便与合理。

在上述领域中，其主要的方法为神经网络、时间序列分析、支持向量机等［2～3］。由于航空机电系统性能大多数分布参数都集中体现出了非线性性质，这决定了只有应用统计学原理方可得出理想结果。支付向量机（SupportVector Machine，SVM）在处理小样本、高维数的非线性问题方面具有很强的适用性，但是SVM算法随着样本量的增大，运算速度会降低［4］。最小二乘支持向量机（LV-SVM）算法既节约了计算时间又降低了计算难度。因此，本文选用LV-SVM预测模型对航空机电系统各性能退化数据的分布参数时间序列进行预测［5］。

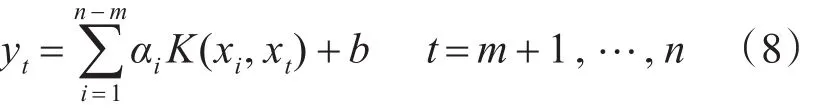
上式（8）中，αi为拉格朗日乘子，K为核函数，b⊂R为常数。由于，则预测模型可表示为

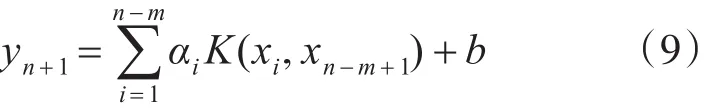
3.2.2 突发故障参数预测

本文将突发故障时间当作响应变量，在回归函数中，退化量并不需要被排除。这说明退化量、故障出现时间的研究能够被放置于回归模型中讨论。借助回归分析，还需要寻找理想的模型——位置-尺度模型［6］，而且它在退化量x等参数的基础上对Y=lnT的分布进行了描述，模型可以使用下面的关系式进行表述：

当中，e的分布和x没有联系。H(e)-e的可靠度函数。μ(x)-位置参数，σ＞0-不变的尺度参数，x，Y的可靠度函数为

针对其中的突发故障时间Th，使用Yh=lnTh的分布，则Th=exрYh的可靠度函数可表示为

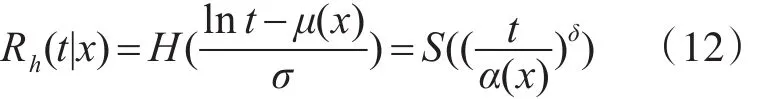
式中，α(x)=exр(μ(x))，δ=1/σ，S(w)=H(ln(w))。利用该模型，式（6）可进一步表示为

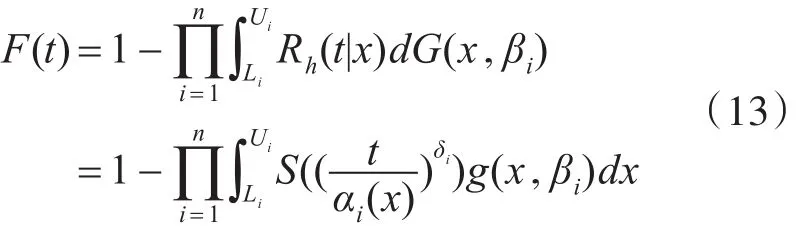
由3.1节分析可知，航空机电突发故障时间Th服从威布尔分布［7］。现对给定退化量x下Yh=lnTh的分布进行分析，由于Th吻合于威布尔分布，则Yh=lnTh服可以吻合于极值分布［8］，其密度函数使用以下的公式进行计算：

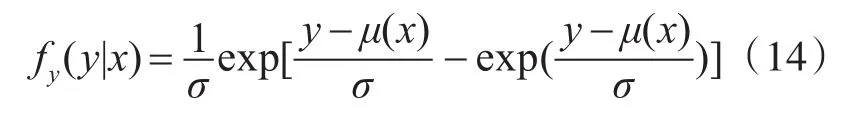
式中，位置参数μ(x)=lnη(x)，尺度参数σ=1/m，若采用标准极值分布［9］进行表示，则Yh如式（15）所示：

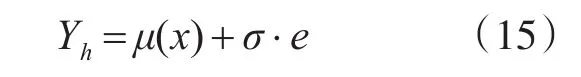
式中，e的密度函数是exр(e-exр(e))。μ(x)以线性为主，令μ(x)=γ1+γ2·x，σ=γ3，则式（16）可表示为

在综合研究了诸多的机电系统后，发现对象系统的故障并不是单一存在的，而是事件、时间的综合表现，即tj(j=1，2，…，K)（退化量）必然在某个tj(j=1，2，…，K)（突发故障时间）中出现，此类关系被称为似然关系［10-12］，由式（17）函数来阐述突发故障数据：

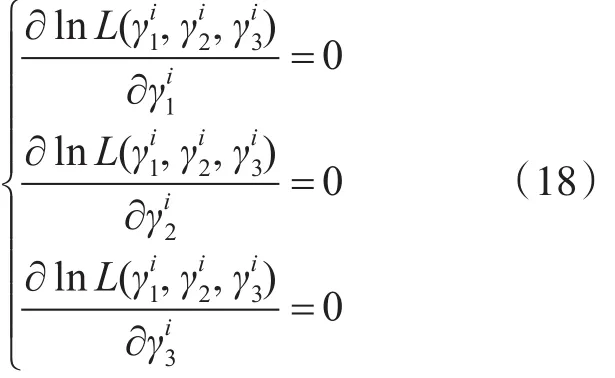
4 实例分析

某海军航空飞行团生产的某型机电系统综合ATS测试数据为例，随机抽取10组机电系统某特征参数作为样本进行故障预测。其测试信息进行测试的时间从2010年持续到2016年，主要是针对性能退化数据和突发故障数据进行测试，因此可根据2010年～2015年的测试信息对机电系统2016年的故障概率进行预测，而且把结果和机电系统的真实情况进行对比，以以便可以检验本次系统设计的有效性和针对性。

结合在工程中的相关经验，可假定航空机电系统的一些性能特征的参数退化中的数据可以吻合于正态分布。以提取的十组机电系统中的特征性能参数2010年的相关的数据为实例，并最终得到以下退化数据（抽取而来）：9.93，10.61，11.00，10.43，12.10，10.22，10.53，10.55，10.67，11.12。按照分布拟合法对抽取值开展验算，并最终得到分布状态。

在集中整理了测试信息后，设该性能退化数据为X，则检验X服从正态分布与否就变为检验假设H0:X～N(μ，σ2)是否成立。按升序排列性能退化数据，并对其进行正态性检验，为方便计算，列表如下。

表1 性能退化数据的正态性检验

由表1可计算得到

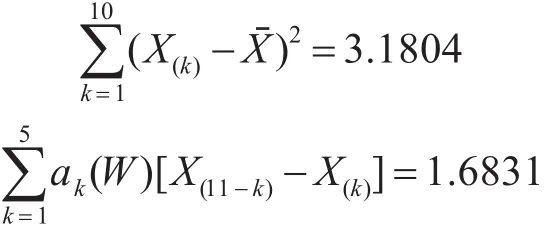
将上述计算结果代入式（7），可得：W=0.8907。

若取显著性水平α=0.05，则通过查阅W检验统计量W的α分位数表Wα可得W10，0.05=0.842。由于W＜W10，0.05，所以在显著性水平α=0.05的情况下，可以接受原假设H0，即可确定2010年测试时某的一些性能参数的特征和正态分布相吻合。

按照提取的十组机电系统某的一些性能参数，针对2010～2015的性能参数进行退化数据的正态性检验，结果表明所有的年份的数据都吻合正态分布。此外，正态性测试也适合剩余数据，相关操作方式如上。通过测算，发现如果结果出现了α=0.05的情况，其余性能特征参数的性能中的退化数据也吻合于正态分布。同理，结合工程中的经验，假定机电系统的突发故障数据仍然使用Копмогоров方法对其中的分布类型进行证实，可得机电系统的突发故障参数服从威布尔分布。

由3.2节分析结果得出，航空机电系统性能退化参数可以吻合于正态分布，所以在针对性能参数进行预测的过程中，也只是需要针对预测均值和方差等指标进行测试。

经过对数据的分析处理，从2007～2015年中，提取了十组机电系统某性能特征参数，并对此类参数进行特殊处理，得到方差、均值。其时间序列为：（10.7160，10.7530，10.7960，10.8000，10.8160，10.8240，10.9340，11.0020，11.0870）和（0.3534，0.3771，0.6871，0.5370，0.5003，0.4050，1.0234，0.5728，0.5980）。首先预测均值μ，选取m=1，相空间重构均值序列的前5个数据，可得样本对Xμ=[10.7160，10.7530，10.7960，10.8000，10.8160，10.8240]T、Yμ=[10.7530，10.7960，10.8000，10.8160，10.8240，10.9340]T。选取RBF函数作为核函数，设定参数γ和δ的搜索区域分别为[0.1，500]和[0.01，100]，采用交叉检验和网格搜索算法进行求解，可得最优参数δ2=3.2463，γ=116.4963。使用LS-SVM训练对样本执行输入和输出等操作，可以取得均值μ的预测的回归直线，如下图。得到训练完毕的LS-SVM回归函数之后，即可开始预测输入样本10.7530， 10.7960， 10.8000， 10.8160， 10.8240，10.9340]T。预测结果显示实测值与预测值基本吻合：同理，可以预测性能退化数据的方差时间序列，结果显示绝对误差小于-0.05，相对误差小于0.009。

图1 均值预测回归曲线

分析2007年～2015年的故障数据可以发现，提取了十组机电系统的记录，持续的时间为2008年～2015年，其故障的总数分别为2,2,2,2,1,1,1,1。因为对于机电系统进行了实时的测试，所以需要以天为单位进行测试，所以提取的十组数据的突发时间可以表示为具体的天数。以某退化特征参数的退化量为例，与突发故障时间的对应关系可得，同时可以得出突发故障与退化量的相关参数的估计值。明确了数据的分类模型和相应的参数，即可根据式（13）对机电系统在2015年和2016年的故障概率进行预测。结果发现，实际进行测评的结果和预测值是基本上一致的，所以建立的故障预测模型是合理而有效的。

5 结语

文章中，借助于航空机电系统中关系复杂的退化性质，集中论述了退化发生频率、故障出现时间的数学关联，引入航空系统的故障和预测模型，而且针对退化数据中的分布参数的小样本、非线性的特征，使用最小支持向量机预测的算法针对故障进行了预测，基于退化量与突发故障的相关性，预测了突发故障预测模型相关参数。最后实例分析结果表明：本文设计的方法预测精度更高，更加合理有效。

［1］吴翊，李永乐，胡庆军.应用数理统计［M］.北京：国防科技大学出版社，2008.

［2］张广明，袁宇浩，龚松建.基于改进最小二乘支持向量机方法的短期风速预测［J］.上海交通大学学报，2011，45（8）：1125-1129.

［3］丛林虎，徐廷学，杨继坤，董琪.导弹退化故障预测方法研究［J］.电光与控制，2014，21（5）：78-82.

［4］洪杰，韩磊，苗学问，马艳红.基于支持向量机的滚动轴承状态寿命评估［J］.北京航空航天大学学报，2010，36（8）：896-899.

［5］唐杰明，刘俊勇，杨可等.基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测［J］.电网技术，2009，33（3）：63-65.

［6］Lawless J F.寿命数据中的统计模型与方法［M］.北京：中国统计出版社，1998.

［7］苏春，张恒.基于性能退化数据和竞争失效分析的可靠性评估［J］.机械强度，2011，33（2）：196-200.

［8］孙绍辉.面向预知维修的航空发动机可靠性评估与预测研究［D］.南京：南京航空航天大学，2013.

［9］GOLDSTEIN M，WOOFF D.Bayes linear statistics，theo⁃ry and methods［M］.New York：Wiley Publisher，2007.

［10］喻天翔，孙玉秋，张祖明.多模式失效的机械零件可靠度计算新理论［J］.机械工程学报，2003（03）：34-35.

［11］苏春，张恒.基于性能退化数据和竞争失效分析的可靠性评估［J］.机械强度，2011（02）：22-23.

［12］李方方，赵英凯，颜昕.基于Matlab的最小二乘支持向量机的工具箱及其应用［J］.计算机应用，2006（26）：358-360.