基于角点检测与特征点配准的图像拼接算法∗

李养胜 李 俊

（陕西工业职业技术学院 咸阳 712000）

1 引言

图像拼接在全景图像导航、机器人、智能交通、公共安全和工业视觉检测等领域有着广泛的应用［1］。图像拼接的主要过程为：图像预处理、图像角点检测、图像配准、建立变换模型、统一坐标变换和图像融合；算法基本上可以分为两类：基于频域的方法（相位相关方法）和基于时域的方法［2］。本研究的对象是背景相对复杂，特征杂乱微弱的轴承目标，且图像重叠区域较少，在此背景下，本文展开针对图像准确拼接研究。

在图像拼接方面，国内研究人员已经取得了一定研究成果，如张莹［3］提出基于ORB算法和OECF模型的快速图像拼接算法，利用SIFT算法提取特征点，再用ORB算法获取特征点的二进制码串描述子进行匹配，而后通过投影变换模型获取参数，最后估计摄像机的光电转换函数，利用模型参数对拼接图像进行色彩调整，解决了多幅图像拼接中颜色不一致的问题。但是，此技术未充分考虑复杂背景的干扰，往往影响了拼接准确性。陈月［4］提出了基于SIFT特征矢量图的快速图像拼接系统，首先结合相位相关算法，确定待拼接图像的重叠区域，限定SIFT特征点检测范围；然后考虑特征点的空间位置信息，构建SIFT特征矢量图像，以便在特征匹配时限制匹配点的搜索范围，快速获得匹配点。然而，这种技术未考虑重叠区域较少的情况，当待拼接图像重叠区域较少时，往往不能达到准确拼接的目的。

为达到提高算法拼接准确度的目的，本研究提出基于角点检测与特征点配准的图像拼接算法。利用输入图像得Hessian矩阵来构建尺度空间，通过积分图像转换，设计基于surf的角点检测算子，精准定位图像拼接参考点的目的。然后，根据角点匹配参数，推导计算出单应性矩阵，进行两幅图像间拼接转换处理，进一步精确并全自动化图像拼接结果。最后，基于软件开发环境VS2015实现算法，并系统集成。最后，测试了所提算法的拼接性能。

2 本文图像拼接算法

背景相对复杂，特征杂乱微弱的轴承目标，且图像重叠区域较少。首先，基于图像采集器，分别读取两帧带有少量重叠的轴承目标图像，作为待拼接的他对象。然后基于角点检测与图像配准的图像拼接算法。首先，根据图像Hessian矩阵，构建尺度空间，通过积分图像转换，设计基于surf的角点检测算子，精确定位角点，达到精准定位图像拼接参考点的目的。然后，根据角点匹配参数，推导计算出单应性矩阵，进行两幅图像间拼接转换处理，进一步精确并全自动化图像拼接结果。最后进行功能测试和稳定性测试，实验验证本系统算法，本文算法流程如图1所示。待处理图像如图2所示，可见轴承目标特征微弱，背景复杂，且重叠部分较少。

2.1 基于surf的角点检测算子

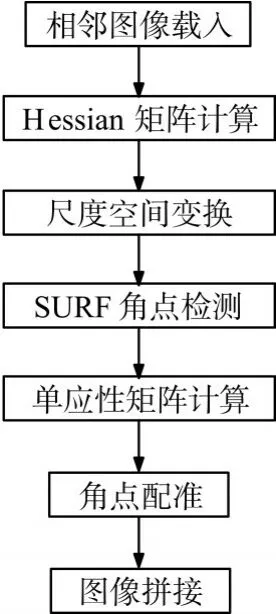
图1 本文图像算法过程

图像拼接准确的前提是准确检测到图像重叠区域的角点，而角点往往具有不明显性，本研究基于Hessian矩阵和积分图像，设计出基于surf的角点检测算子。SURF算法是对SIFT算法的一种改进，SURF算法对积分图像进行操作，卷积只和前一幅图像有关，其降采样的方法是申请增加图像核的尺寸，SURF算法允许尺度空间多层图像同时被处理，不需对图像进行二次抽样，从而提高算法性能［5～7］。首先构建Hessian矩阵：

式中f（z，y）代表图像函数，x，y代表横、纵坐标，H矩阵判别式为

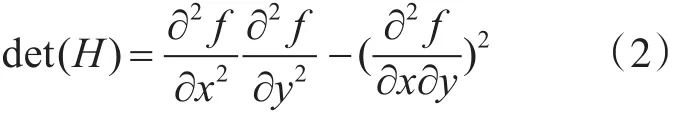
其中，g代表H矩阵的特征值和判别式，可以利用判定结果的符号将所有点分类，根据判别式取值正负，来判别该点是或不是极值点，用图像像素l（x，y）代替函数值f（x，y），选用二阶标准高斯函数作为滤波器，通过特定核间的卷积计算二阶偏导数，这样便能计算出H矩阵的三个矩阵元素的值，从而计算出H矩阵［8］。

图2 待处理原图

图像尺度空间代表图像在不同解析度下的表示，表述为一个图像金字塔，其中输入图像函数反复与高斯函数的核卷积并反复对其进行二次抽样，SURF算法申请增加图像核的尺寸，允许尺度空间多层图像同时被处理。经过Hessian矩阵处理的像素点与其3维领域26个点进行大小比较，若该像素点为26个点中的最大值或者最小值，则判为特征点［9］。

采用本研究角点检测算子，处理图2，得图3，角点定位在图像重叠区域的特征点，可见本研究角点检测准确。

2.2 基于单应性矩阵的图像配准

得到图像重叠区域角点后，需进行配准，本研究采用单应性矩阵，完成图像拼接。矩阵重要作用是将空间中的点变换到另一个空间中，单应性变换是图像矩阵变换其中一种方法，单应性变换的目标是通过给定的几个点（通常是4对点）来得到单应性矩阵，下面是单应性矩阵的推导过程［10］：

矩阵H将拼接前图像上的一个点坐标（x，y，1）映射成拼接后图像上点坐标(x1，y1，1)，进一步展开：

一般所选取的角点是相对于其领域表现出来具有某种奇异性的像素点，特征点往往容易被提取到，但是特征点所包含的信息相对较少，只能反映出其在图像中的位置坐标信息［11～12］。本研究进一步精确化角点匹配，推导H矩阵参数，完成图像拼接：

式中H矩阵代表单应性变换参数，后续实验中详细给出。最后采用本研究算法，结合特征点检测和单应性配准，完成图像拼接。采用本节算法，结合上节特征点检测结果，处理图2，得到图4，位图像配准结果，可见配准准确；得到图5，为图像拼接结果，可见拼接准确。

图3 角点检测结果

图4 图像配准结果

图5 图像拼接结果

3 实验与讨论

为了体现本文算法的优势，将拼接性能较好的技术-文献［3］、文献［4］设为对照组，本文系统基于VS平台开发实现，软件界面见图6（a）。算法实验参数如：h11=3.2431，h21=3.7504，h31=14.2226，h21=2.8158，h22=1.5170，h23=12.7276，h31=22.0293，h32=24.0287，h33=21.0323。

待拼接图像，如图6（b）所示，图像重叠区域少，背景复杂，本研究基于surf进行角点检测，根据单应性矩阵变换，进一步准确角点配准，如图7所示，可见本研究，重叠区域角点检测和配准正确，如图8所示，可见本研究，拼接正确。

图6 本次实验的软件与测试对象

而利用对照组文献［3］技术，利用SIFT算法提取特征点，通过投影变换模型获取参数，利用模型参数对拼接图像进行色彩调整。但是，此技术未充分考虑复杂背景的干扰，往往影响了拼接准确性，如图9所示，可见存在拼接失误。

图7 本研究角点配准图

图8 本文算法的拼接结果

图9 文献［3］算法的拼接结果

利用对照组文献［4］技术，首先结合相位相关算法，限定SIFT特征点检测范围；构建SIFT特征矢量图像，快速获得匹配点，然而，这种技术未考虑重叠区域较少的情况，当待拼接图像重叠区域较少时，往往不能达到准确拼接的目的，如图10所示，可见存在拼接失误。

图10 文献［4］的拼接结果

4 结语

为了解决当前图像拼接算法在背景复杂和重叠区域较少的情况下，导致算法拼接不准确的问题，本文分别从角点检测与单应性配准的角度出发，提出了基于角点检测与图像配准的图像拼接算法。根据图像Hessian矩阵，构建尺度空间和图像转换，设计基于surf的角点检测算子，精确定位角点。根据单应性矩阵计算，进行图像拼接。最后，基于VS实现算法，并系统集成，达到准确图像拼接的目的。实验结果表明：本文拼接算法具有更高准确度。

［1］A.Laraqui，A.Baataoui，A.Saaidi.Image mosaicing us⁃ing voronoi diagram［J］.Multimedia Tools and Applica⁃tions，2017，76（6）：8803-8826.

［2］Zhicheng Wang，Yufei Chen，Zewei Zhu.An automatic panoramic image mosaic method based on graph model［J］.Multimedia Tools and Applications，2016，75（5）：2725-2740.

［3］张莹.基于ORB算法和OECF模型的快速图像拼接研究［J］. 计算机工程与应用，2017，13（21）：71-76.

［4］陈月，基于SIFT特征矢量图的快速图像拼接方法［J］.吉林大学学报（理学版），2017，8（15）：42-47.

［5］Anto A.Micheal，K.Vani，S.Sanjeevi.Automatic Graben Detection in Lunar Images Using Hessian Technique［J］.Journal of the Indian Society of Remote Sensing，2014，42（2）：445-451.

［6］詹曙，王少武，蒋建国.基于尺度限制SURF的图像配准［J］. 电 子 测 量 与 仪 器 学 报 ，2013，27（10）：963-967.

［7］顾漪，王保平.基于旋转SURF算子的图像配准新方法［J］.计算机测量与控制，2017，25（7）：197-201

［8］杨加东.一种基于图像展开与拼接的精密轴承表面缺陷光学检测方法［J］. 机床与液压，2017，16（4）：181-185.

［9］孙苗苗.基于图像拼接和帧间差分输电线路图像分割方法［J］. 红外技术，2017，17（12）：47-50.

［10］李玉峰.基于区域分块与尺度不变特征变换的图像拼接算法［J］. 光学精密工程，2016，16（4）：181-185.

［11］Zong-yan Li，Li-mei Song，Jiang-tao Xi.A stereo matching algorithm based on SIFT feature and homogra⁃phy matrix［J］.Optoelectronics Letters，2015，11（5）：390-394.

［12］陈月.图像局部特征自适应的快速SIFT图像拼接方法［J］. 中国光学，2016，20（12）：71-76.