空天飞行器弹道/轨道一体化设计

方群，刘怡思，王雪峰

1.西北工业大学 航天学院，西安 710072 2.西北工业大学 航天飞行动力学技术国家重点实验室，西安 710072

空天飞行器是航空航天飞行器的简称，是航空技术与航天技术高度结合的飞行器。在现代空天飞行器的飞行任务中，越来越多地涉及到了大气层内外的穿梭，因此弹道/轨道一体化设计的需求也越来越凸显[1]。弹道/轨道一体化设计具有精度高、易于优化的优点，同时也能从宏观角度整体、全面地描述和设计空天飞行器的整个任务轨迹[2]。目前，针对弹道/轨道一体化设计的研究主要是集中在任务一体化和参数一体化上：任务一体化的设计方法是根据飞行器的飞行任务将飞行轨迹分为弹道段和轨道段分别建模设计，然后将设计结果按照任务要求进行拼接，最终得到完整的弹道/轨道设计结果；而参数一体化的设计方法是将轨道六要素用弹道的相关参数来表示，从而统一整个弹道段和轨道段参数，将弹道和轨道的设计转化为弹道参数的设计[2-5]。上述方法存在的主要问题是没有建立统一的空天飞行器动力学模型，因此不能真实准确地描述空天飞行器的受力和运动情况。同时弹道方程较为复杂，参数数量多，不易于优化。

由于弹道是飞行器在大气层内飞行时质心的运动轨迹，而轨道则是飞行器运动在外层空间中质心的运动轨迹，因此两者虽然都是表征飞行器运动轨迹的特征曲线，但有着区别较大的飞行环境，以及不同的动力学特性。为此针对大气层内和大气层外力学环境不同难以统一动力学建模的问题，罗亚中等采用将轨迹拆分再拼接的建模方法[4-6]，将整个任务轨迹拆分为弹道段和轨道段来分别求解，最后将所得结果拼接获得整个空天飞行器的轨迹解。该方法的特点是利用拆分再拼接的方法将任务轨迹拆分为弹道段和轨道段，使得原本变量耦合的复杂问题变成了采用两种算法以一定的时间顺序分别求解两个相对简单的问题，所建立的算法和模型具有较广泛的适应性。但是由于这种简单的拆分拼接所反映的是一种单一任务过程，针对多次重复往返大气层的任务该方法将难以反映真实情况，同时这种建模方法在弹道和轨道的转换段精度较低，并且由于这种方法要进行弹道和轨道的联合设计，所以如果有一方设计结果不理想，将会影响到另一方的设计结果和精度。另外这种分段设计再拼接的方法也难以进行轨道的优化设计。

针对上述方法优化难以进行的问题，张卫华等提出了一种弹/轨参数一体化建模和优化方法[3,7]。该方法利用弹道参数和轨道参数之间的转化关系来统一处理任务轨迹，利用弹道参数来表示轨道根数，从而实现了将整个过程转化为对弹道发射参数以及控制的优化。该方法实现了弹道/轨道的参数一体化，从而使得对任务轨迹的整体优化问题转化为对发射初始参数和控制律的优化问题，得到了满足任务需求的优化结果。然而，这种方法依然没有摆脱将任务轨迹分解为弹道和轨道简单叠加的建模方法，将一个实际上存在较强耦合的问题人为地线性化，一个实际上较为复杂的任务进程顺序化、简单化，从而导致无论是建模的精度还是优化的程度都存在着明显的不足。

由此可见，目前针对空天飞行器轨道设计所采用的方法主要是将飞行器的任务轨迹拆分为弹道段和轨道段，对弹道段和轨道段分别进行设计，再拼接产生空天飞行器轨道设计结果。这种方法计算效率较低，并且不利于后续的优化设计。为此亟待解决针对空天飞行器的弹道/轨道一体化建模以及整体优化设计的问题。本文首先提出采用轨道方程统一描述空天飞行器弹道/轨道一体化建模思想，即将除引力之外的合力都视为摄动力，并写入轨道摄动方程中，从而建立弹道/轨道一体化动力学模型。然后在此基础上，提出基于轨道设计反方法的弹道/轨道一体化设计方法。仿真分析表明本文提出的弹道/轨道一体化设计方法是可行和有效的，为空天飞行器的轨道设计开辟了新的思路。

1 弹道/轨道一体化设计

1.1 极坐标下的飞行器动力学建模

假设飞行器处于二体引力场中，即飞行器只受中心天体地球引力的影响，且中心天体地球对飞行器的引力为指向地心，引力大小与飞行器到地心距离的平方成反比，飞行器所受的其他力全部作为摄动力来表述。建立以地心为极点，从地心出发沿着赤道向某方向的射线作为极轴的二维极坐标下的轨道摄动方程为

(1)

式中：r为飞行器的位置矢量，r=‖r‖为飞行器位置矢量的模，表示飞行器到坐标原点即地心的距离；m为飞行器的质量；f表示除了引力之外飞行器所受的其他力的合力；μ为引力常数。

图1为极坐标下的飞行器受力图，O表示中心天体，A表示飞行器的质心，极角θ和距离r为两个自变量，表征飞行器的位置，V为飞行器的速度。令R为飞行器径向单位矢量，θ为法向单位矢量，γ为V与θ的夹角。

由r=rR，有

(2)

(3)

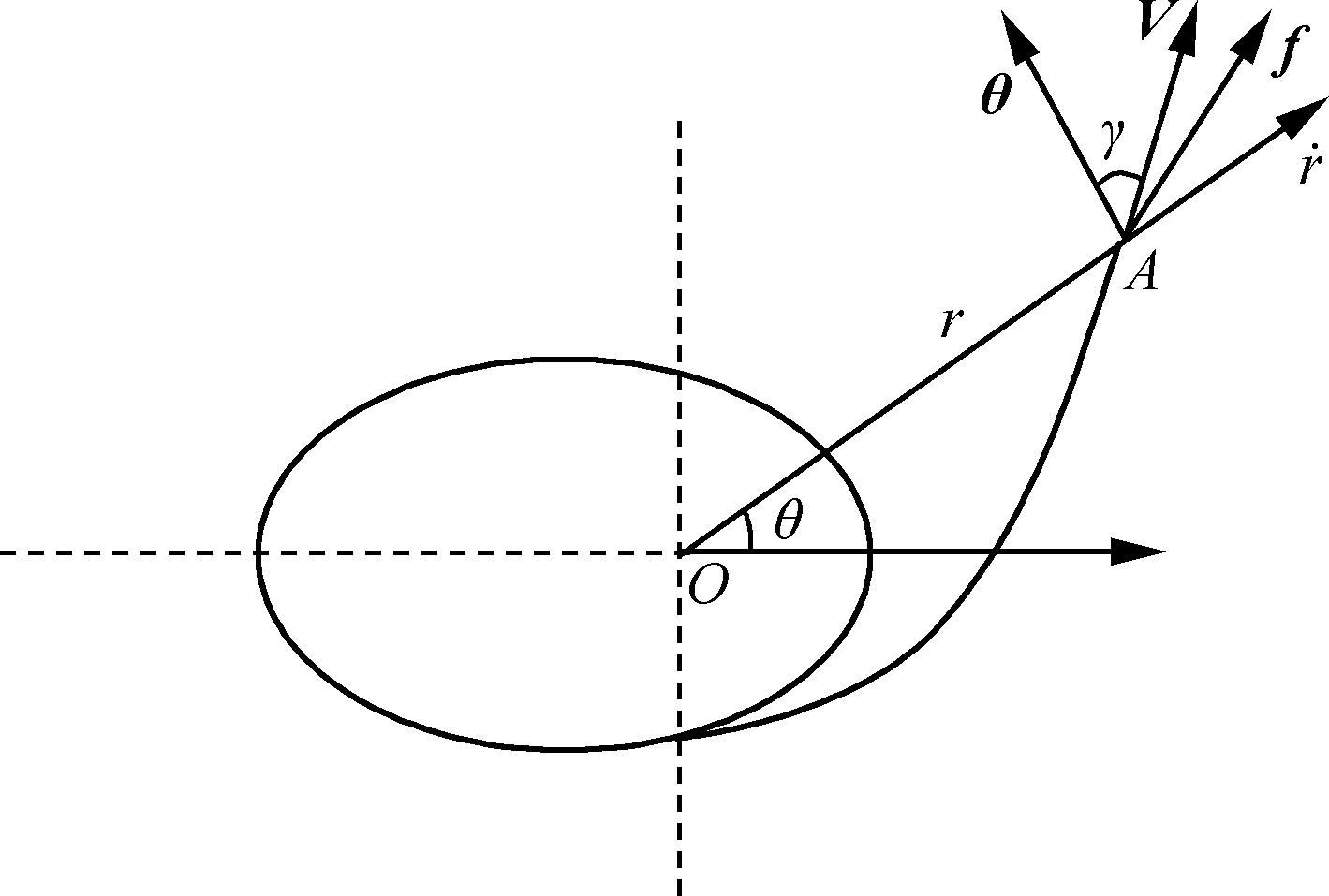
图1 极坐标下的飞行器受力Fig.1 Forces of aircraft in polar coordinate

将式(3)代入式(1)，有

(4)

将式(4)沿径向和法向展开，有[8-11]

(5)

式中：fjing和ffa分别为除引力外其他作用力在径向和法向的投影。

飞行器除引力之外的其他受力如图2所示。图中：A点表示飞行器的质心，两条虚线表示θ和R的单位矢量方向，L是飞行器所受的升力，D是飞行器所受的空气阻力，F为飞行器的推力，假设发动机没有安装偏差角，则迎角α即为推力方向与V之间的夹角。

将除引力之外的气动力和推力代入式(5)，有

(6)

根据γ的定义，有

(7)

而位置矢量的极坐标形式为r=(rcosθ,rsinθ)，则有

(8)

将式(8)代入式(7)，可得

(9)

图2 飞行器所受除引力之外的其他力Fig.2 Forces of aircraft except gravity

将式(9)代入式(6)，有

(10)

定义无量纲化地心距、时间、速度以及各力分别为

(11)

(12)

(13)

(14)

式中：r0为地球半径；v为飞行器速率。经无量纲处理后，式(10)可表示为

(15)

式中：z′、z″、θ′和θ″分别为各个变量对广义时间τ的一、二阶导数。

由式(12)，有

(16)

由此可得

(17)

将式(16)、式(17)代入式(15)，得极坐标下飞行器无量纲动力学模型为

(18)

1.2 无量纲处理

为了编程方便，将式(18)写成便于积分的形式，即

(19)

为了实现弹道/轨道的一体化设计，需要将动力学模型式(19)转化为只含有状态变量z、z′、θ、θ′和时间τ以及控制变量f、α的方程组，其他参数包括m、l和d等需要用状态变量、控制变量与飞行器的特性参数来表示，其具体过程如下所述。

1) 气动力

升力、阻力的基本计算模型为

(20)

(21)

式中：CL为升力系数；CD为阻力系数；ρ为大气密度；s为飞行器横截面积。

选取某型号飞行器为研究对象，对该飞行器在雷诺数Re=1.34，马赫数Ma=8.02，努森数Kn=0.001下的气动力系数进行了仿真计算，其结果如表1所示。

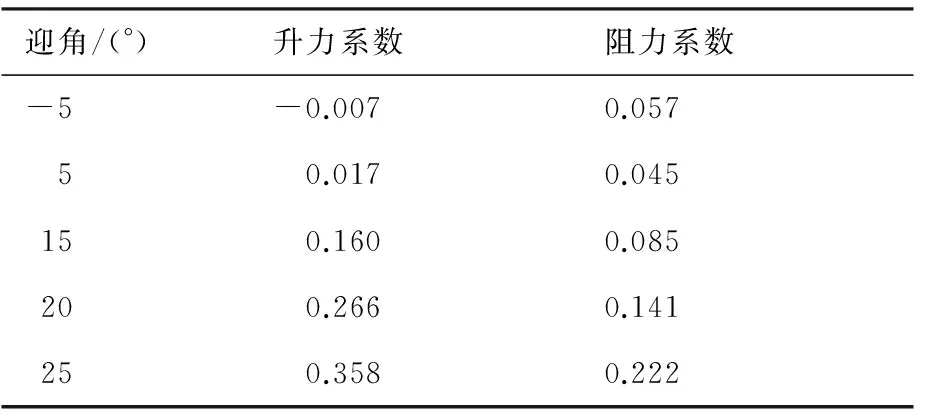
表1 某飞行器的气动参数计算结果

经拟合之后得到升力系数CL及阻力系数CD的表达式为

CL=1.253 4(α-γ)2+

0.259 6(α-γ)+0.006 1

(22)

CD=1.346 2(α-γ)2-

0.154 7(α-γ)+0.033 2

(23)

2) 飞行速率

飞行速率的无量纲表达式为

(24)

将式(17)代入式(24)，得飞行速率的无量纲表达式为

3) 推 力

由于本文推力是作为设计量和优化量来处理的，因此推力可以看作可控制力，为此只需要给出推力约束条件即可，即

{F∈[0,Fmax]

Is=uef

(25)

式中：Fmax为最大推力；Is为发动机的比冲；uef为等效喷气速度。

4) 飞行器质量

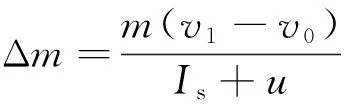
(26)

式中：v0、v1分别为飞行器初速率和末速率。

将式(12)代入式(26)，则有

(27)

式中：v为无量纲化之前的飞行器速度，由式(24)确定，由此可得

(28)

式中：v′为飞行速度对广义时间的导数。

5) 无量纲的一体化模型

将式(20)～式(28)整理之后,得到式(19)可积分的形式为

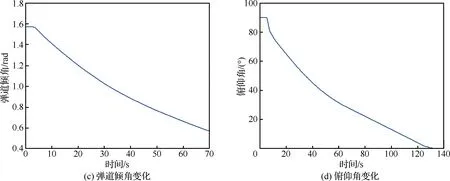
图4 弹道设计仿真结果Fig.4 Simulation results of trajectory design

3.2 轨道设计

将3.1节弹道设计的结果作为初值，目标轨道设定为轨道高度为35 860 km的圆轨道，即地球同步轨道。取距离单位为1 DU=1Rearth，Rearth为地球半径,时间单位为1 TU=806.8 s，推力约束为Fmax=0.01 DU/TU2。得到仿真结果如图5和图6所示，图5为应用形状方法得到的飞行器轨迹，图6为飞行器推力加速度ac随时间t变化的曲线。

由于本节的设计是将3.1节设计结果的末状态作为初值，所以其与3.1节的弹道设计结果能够自然地衔接，如此就完成了整个弹道/轨道的一体化设计。

图5 形状轨道Fig.5 Shape-based trajectory

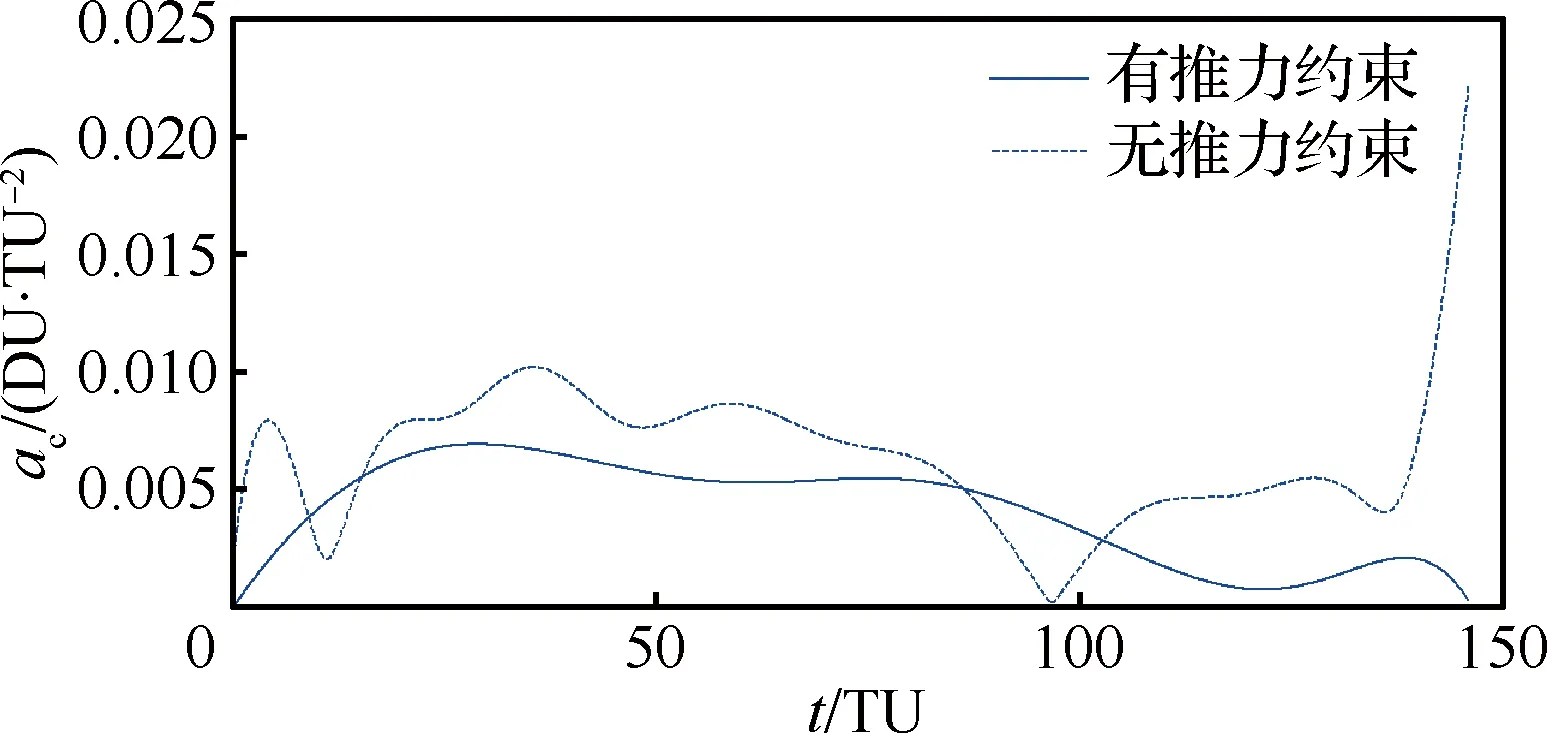
图6 飞行器轨道机动所需的推力加速度Fig.6 Required thrust acceleration using aircraft orbit maneuver

4 结 论

1) 提出了采用轨道方程统一描述弹道/轨道的思想，即将除引力之外的合力都视为摄动力，并写入轨道摄动方程的摄动力项中，通过整合连续推力、气动力、引力以及摄动力等多种作用力，建立弹道/轨道一体化动力学模型，为空天飞行器一体化轨道设计建立基础。

2) 为了解决目前存在的弹道段轨迹设计方法与轨道段轨迹设计方法不统一的问题，将轨道设计中的反方法设计思想应用于弹道设计中，提出了一种基于弹道/轨道一体化模型的弹道设计反方法，使得同时从模型与方法的角度体现一体化的设计思想。

3) 将弹道段的终端状态参数值作为初值，目标轨道参数值作为终值，通过合理选择轨道转移时间和绕转圈数，采用基于傅里叶级数展开的形状方法，完成了轨道段轨迹的设计。由于是将弹道段的末状态作为轨道段的初值，所以轨道设计结果能够自然地与弹道衔接，形成了整个弹道/轨道的一体化设计结果。

4) 本文提出的弹道/轨道一体化设计方法的适用性和限制条件为：① 由于针对三维空间的轨迹设计需要考虑姿态运动方程，目前还不能实现统一建模，故现阶段该方法只能应用于二维平面的轨迹设计；② 应用傅里叶级数法设计轨道段，需要事先给出一个飞行时间。与此同时，考虑到傅里叶级数的项数对计算效率和精度的影响，项数不能无限增加。

虽然目前本文方法受技术瓶颈的制约还存在着应用局限性，但给未来先进空天飞行器的弹道/轨道一体化设计提出了新的思路和技术途径。随着相关技术问题的解决，方法的适用性将会得到提高。

[1] 赵瑞安.空间武器轨道设计[M]. 北京: 中国宇航出版社, 2008: 176-178.

ZHAO R A. Space weapon orbit design[M]. Beijing: China Astronautic Press, 2008: 176-178 (in Chinese).

[2] 黄文博, 张强, 肖飞，等. 空间快速响应航天器轨道/弹道一体化规划[J]. 固体火箭技术, 2012, 35(1): 11-16.

HANG W B, ZHANG Q, XIAO F, et al.Orbit-trajectory integrated programming for operationally responsive space spacecraft[J]. Journal of Solid Rocket Technology, 2013, 35(1): 11-16 (in Chinese).

[3] 肖飞, 向敏, 张卫华. 多级运载火箭总体/弹道/轨道一体化设计与优化[J]. 空军工程大学学报， 2008, 9(5): 19-23.

XIAO F, XIANG M, ZHANG W H. Orbit trajectory and system integration design and optimization of multi-stage solid rocket[J]. Journal of Airforce Engineering University, 2008, 9(5): 19-23 (in Chinese).

[4] 罗亚中, 唐国金, 梁彦刚, 等.近地轨道运载火箭轨迹/总体参数一体化设计与优化[J]. 中国空间科学技术， 2003，10(5)： 16-32.

LUO Y Z, TANG G J, LIANG Y G, et al. Integrated optimization design for trajectory/system parameter of low earth orbit launch vehicle[J]. Chinese Space Science and Technology, 2003, 10(5): 16-32 (in Chinese).

[5] 罗亚中, 唐国金, 梁彦刚. 基于分解策略的SSO发射轨道遗传全局优化设计[J]. 航空学报， 2004， 25(5)： 443-446.

LUO Y Z, TANG G J, LIANG Y G. Decomposition approach and genetic algorithm based global optimization of launch trajectory for sun synchronous orbit[J]. Acta Aeronautica et Astronautica Sinica, 2004， 25(5)： 443-446 (in Chinese).

[6] 罗亚中, 唐国金, 梁彦刚, 等. GTO发射轨道的两级分解全局优化设计策略[J]. 中国空间科学技术， 2004, 24(4)： 36-46.

LUO Y Z, TANG G J, LIANG Y G, et al. Bilevel decomposition based global optimization approach for launch trajectory of GTO launchers[J]. Chinese Space Science and Technology, 2004,24(4): 36-46 (in Chinese).

[7] 杨希祥, 江振宇, 张卫华. 小型运载火箭大气层飞行段飞行程序设计研究[J]. 飞行力学, 2010, 28(4): 68-72.

YANG X X, JIANG Z Y, ZHANG W H. Flight program design for small launch vehicle in atmosphere flight stage[J]. Flight Dynamics, 2010, 28(4): 68-72 (in Chinese).

[8] BATTIN R H. An introduction to the mathematics and method of astrodynamics[M]. New York: AIAA Education Series, 1987: 408-418.

[9] BATTIN R H, FILL T J. Extension of gauss method for the solution of Kepler’s equation[J]. Journal of Guidance, Control and Dynamics, 1979, 2(5-6): 190-195.

[10] BATTIN R H.A scrapbook of beautiful equations and great ideas[C]∥ Astrodynamics Symposium, 2000:423-433.

[11] 郑莉莉. 连续推力作用下的机动轨道设计与优化[D]. 西安: 西北工业大学, 2011: 15-43.

ZHENG L L. Orbit design and optimization for spacecraft maneuver under continuous thrust[D]. Xi’an: Northwestern Polytechnical University, 2011: 15-43 (in Chinese).

[12] TAHERI E, ABDELKHALIK O. Shaped-based approximation of constrained low-thrust space trajectory using Fourier series[J]. Journal of Spacecraft and Rockets, 2012, 49(3): 535-546.