CRM-WB风洞模型高阶精度数值模拟

王运涛，孟德虹，孙岩，李伟

1.中国空气动力研究与发展中心 计算空气动力学研究所， 绵阳 621000 2.中国空气动力研究与发展中心 空气动力学国家重点实验室， 绵阳 621000

AIAA阻力预测研讨会[1-4](Drag Prediction Workshop， DPW)吸引了世界范围内空气动力学研究工作者的广泛参与，已成为CFD验证与确认研究领域最重要的国际合作之一。2012年6月召开的第5届DPW(DPW Ⅴ)采用了CRM (Common Research Model)[5]翼身组合体构型作为基准研究模型，并在NASA Langley的NTF(National Transonic Facility)风洞、NASA Ames的TWT(Transonic Wind Tunnel)中开展了相应的风洞试验[6-7]。DPW Ⅴ上，基于雷诺平均Navier-Stokes(RANS)方程和2阶空间离散精度的计算方法，来自世界各地的22家研究机构共提供了57组CRM翼身组合体构型计算结果[8]，对这些计算结果的统计分析表明，设计升力系数下，来流迎角的计算结果普遍低于相应的试验结果，低头力矩的计算结果普遍大于相应的试验结果；相同迎角下，升力系数、低头力矩的计算结果普遍大于相应的试验结果。本文作者在前期研究工作[9]中采用5阶空间离散精度的WCNS(Weighted Compact Nonlinear Scheme)开展了CRM翼身组合体构型的数值模拟，计算结果与试验结果之间同样存在较大的差异。

Levy等在文献[8]中总结了导致CRM翼身组合体构型气动特性风洞试验与计算结果之间差异的主要因素包括：数值计算模型中没有包括试验模型在气动载荷作用下的静气动弹性变形，数值计算模型没有包括风洞模型尾部支撑装置，数值模拟中没有考虑风洞试验中固定转捩位置等。基于风洞试验中测量得到的风洞模型静气动弹性变形数据，David[10]采用二阶精度计算方法和结构网格技术研究了CRM翼身组合体构型静气动弹性变形对数值模拟结果的影响；Keye等[11]采用2阶精度格式、非结构网格技术和流固耦合方法研究了静气动弹性变形对CRM翼身组合体构型数值模拟结果的影响；但上述研究工作所采用的计算模型中并没有包含模型支撑装置。2016年6月召开的第6届DPW(DPW Ⅵ)选择了包括静气动弹性变形的CRM翼身组合体构型作为基准研究模型，以期提高数值模拟结果与风洞试验结果的吻合程度，来自世界各地的25家研究机构共提供了54组计算结果[12]。DPW Ⅵ数值模拟结果的统计分析表明，考虑了CRM翼身组合体构型的静气动变形后，气动特性计算结果与试验结果的吻合程度有显著改善，但升力系数、低头力矩系数的计算结果普遍高于试验结果的现象依然存在，计算方法基本采用2阶空间离散精度的差分格式依然没有包含模型支撑装置的影响。

在文献[9]网格收敛性研究工作的基础上，基于DPW Ⅵ组委会提供的CRM翼身组合体数值模拟和NASA NTF风洞的支撑装置数值模拟，本文采用5阶空间离散精度的WCNS和多块对接结构网格技术，开展了CRM翼身组合体风洞试验模型的高阶精度数值模拟，主要目的是采用高阶精度方法，评估风洞模型静气动弹性变形和支撑装置对CRM翼身组合体构型气动特性的影响。

1 CRM翼身组合体风洞模型

CRM构型是由NASA和DPW组织委员会联合设计开发的宽体运输机构型，主要目的是为CFD的验证和确认工作提供基准外形，设计马赫数为0.85、升力系数为0.50。CRM系列构型包括了翼身组合体、翼/身/平尾组合体和翼/身/平尾/挂架/吊舱组合体等不同构型，DPW Ⅴ组委会和DPW Ⅵ组委会均选择了CRM翼身组合体构型做为基准研究模型，不同的是DPW Ⅵ组委会选择的CRM翼身组合体构型包含了不同迎角下风洞试验测量得到的静气动弹性变形。

NASA NTF风洞试验中，CRM翼身组合体试验模型缩比为0.027，基本参数为：模型参考面积Sref=0.279 7 m2;平均气动弦长c=1.891 m;展长b=1.587 m;梢根比λ=0.275;展弦比AR=9.0;1/4弦线后掠角Λc/4= 35.0°;马赫数Ma=0.85;雷诺数Re=5.0×106。图1给出了DPW Ⅵ组委会提供的包含不同来流迎角α下静气动弹性变形的CRM翼身组合体计算模型，同时给出了CRM翼身组合体“刚性”外形的计算模型(图1中红色部分)。在固定迎角下，机翼的静气动弹性变形沿机翼展向逐渐增加；随着来流迎角的增加，机翼的静气动弹性变形逐渐增加；迎角α=3.0°时，翼梢处的弯曲变形为17.4 mm，扭转变形达到-1.1°。为方便讨论，将CRM翼身组合体“刚性”外形计算模型标识为CRM-WB，将包含静气动弹性变形的CRM翼身组合体外形计算模型标识为CRM-WB-A。

风洞模型采用安装于机身后体的叶片尾撑方式固定于风洞迎角变换装置(如图2所示)。由于风洞试验模型后部的迎角变换装置对气动特性的影响属于二次影响[13]，本文的数值模拟没有考虑模型支撑后部的迎角变换装置；对模型叶片尾撑延伸段进行了局部修型处理以避免底部分离导致的计算收敛困难(图2中红色部分)。本文将包含支撑装置和静气动弹性变形的CRM翼身组合体计算模型标识为CRM-WBS-A。

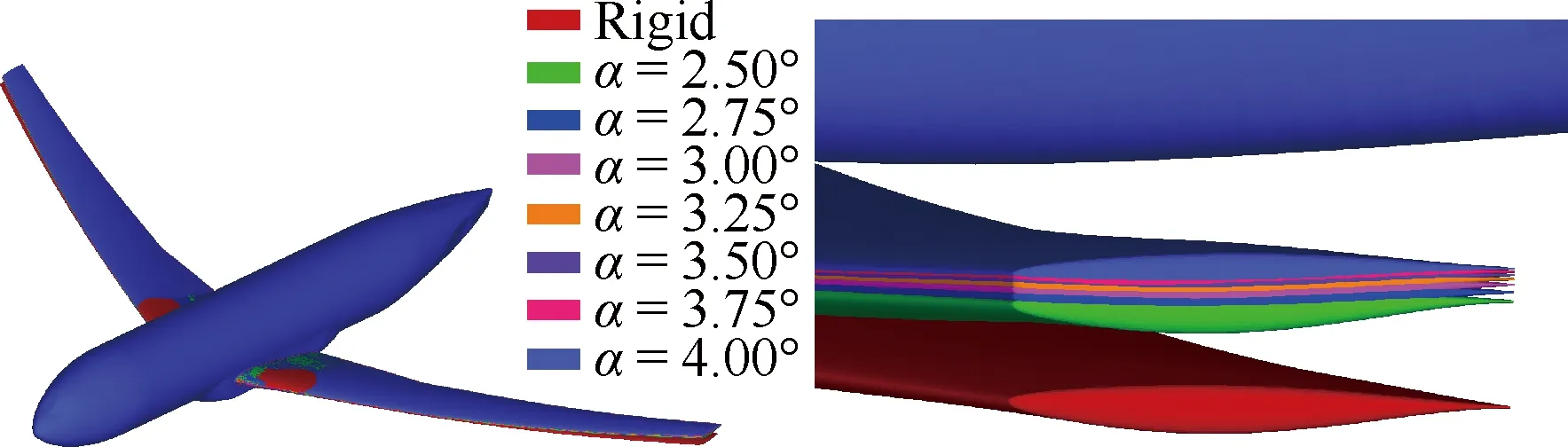
图1 CRM-WB-A构型的计算模型Fig.1 Computational model of configuration ofCRM-WB-A

图2 CRM-WBS-A构型的计算模型Fig.2 Computational model of configuration ofCRM-WBS-A

2 计算网格与高阶精度计算方法

根据DPW组织委员会给出的网格生成指导原则，文献[9]采用粗、中、细和极细4套多块对接结构开展了CRM-WB模型的网格收敛性研究，并获得了具有网格收敛性的气动特性高阶精度计算结果。采用文献[9]中CRM-WB构型的中等网格作为基准网格开展本文的研究工作。CRM-WB构型半模网格规模为8 440 223，物面第1层法向无量纲距离为0.94。利用DPW Ⅵ组委会提供的不同迎角下的静气动弹性变形(如图1所示)，采用与基准网格相同的网格拓扑及网格分布，通过基于径向基[14]与超限插值[15]的复合型动态网格变形方法RBF-TFI[16]，构造了不同来流迎角下的CRM-WB-A构型的计算网格。在此基础上，进一步构造了不同来流迎角下CRM-WBS-A构型对称面计算网格如图3所示，半模网格规模达到了16 133 343。

本文采用有限差分方法离散任意坐标系下的RANS方程组，控制方程的对流项离散采用5阶精度的WCNS，黏性项的离散采用6阶精度中心格式，边界及近边界条件采用单边4阶精度离散，以上方法的详细介绍见文献[17-18]；湍流模型采用Menter 剪切应力输运(SST)两方程湍流模型[19]，数值模拟采用“全湍流”方式；离散方程组的求解采用BLU-SGS方法[20-21]。

图3 CRM-WBS-A构型对称面计算网格Fig.3 Computation grid on symmetric plan of CRM-WBS-A configuration

3 计算结果及讨论

采用CRM-WB、CRM-WB-A和CRM-WBS-A共3种计算模型和高阶精度计算方法，开展设计马赫数下静气动弹性变形和模型支撑装置对数值模拟结果的影响研究，对比数据为NASA 2.5 m×2.5 m NTF风洞试验测力和测压数据[4]。数值模拟来流条件为：马赫数Ma=0.85;基于平均气动弦长的雷诺数Re=5.0×106;迎角α=2.5°～4.0°，迎角间隔Δα=0.25°。

3.1 气动力系数随迎角的变化

图4给出了采用高阶精度计算方法得到的CRM翼身组合体3种计算模型的升力系数CL、阻力系数CD和俯仰力矩系数Cm随来流迎角的变化，同时给出了NASA NTF风洞的测力试验结果。

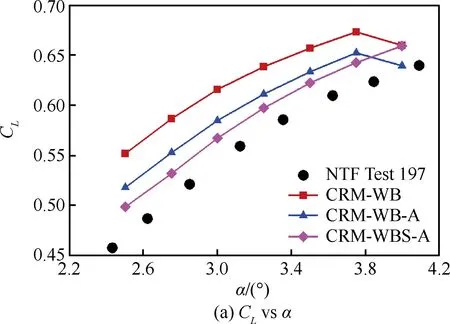
图4 CRM翼身组合体构型气动特性Fig.4 Aerodynamic characteristics of CRM wing-body configuration

在计算迎角范围内，CRM-WB构型与CRM-WB-A构型气动特性的计算结果相比较，静气动弹性变形的影响使得相同迎角下的升力系数、阻力系数和低头力矩系数-Cm均下降，数值模拟得到的2种构型的失速迎角均在3.75°左右。CRM-WB-A构型与CRM-WBS-A构型气动特性的计算结果相比较，进一步考虑了模型尾部支撑后，相同迎角下的升力系数、阻力系数和低头力矩系数进一步下降，失速迎角后移。3种构型的气动特性计算结果相比较，失速迎角以前静气动变形对升力系数和俯仰力矩系数的影响量略高于模型支撑的影响量，而静气动弹性变形和模型支撑对阻力系数的影响量基本相当；CRM-WBS-A构型的气动特性计算结果最接近风洞试验测力结果。计算结果和试验结果仍存在偏差的原因主要是2个方面：① 风洞试验应给出试验结果的误差带并对风洞试验结果的各种修正方式作进一步的研究。② 风洞试验在机翼、机头粘贴了转捩带，而本文的数值模拟采用的是全湍流方式。

3.2 机翼表面压力系数分布 (α=3.0°)

图5给出了迎角α=3.0°时，采用高阶精度计算方法得到的CRM翼身组合体构型3个典型展向位置机翼剖面的压力系数Cp分布曲线，同时给出了NTF风洞相邻迎角的测压数据[4]，图5中横坐标x为机翼流向无量纲距离，η为机翼展向无量纲距离。

从图5可以看出，在内侧机翼(η=0.131、0.397)的位置，静气动弹性变形使得机翼上翼面激波位置略微前移，对其他位置的压力分布基本没有影响；而模型支撑装置使得机翼上翼面的激波位置明显前移。在η=0.727站位，静气动弹性变形使得机翼上翼面激波位置前移、激波位置以前的负压明显下降， 机翼下翼面50%弦长前的压力略有增加；模型支撑装置使得上翼面的激波位置显著前移。在机翼梢部(η=0.950)的位置，静气动弹性变形对压力分布的影响与η=0.727站位类似；而模型支撑装置使得上翼面流动结构发生显著变化，机翼上翼面出现了明显的双激波结构。总之，由于静气动变形导致机翼负扭转角由翼根到翼梢逐渐增加，静气动弹性变形对机翼表面压力系数分布的影响也由翼根到翼梢逐渐增加，主要使得机翼上表面激波位置前移和外侧激波位置以前的负压值下降；支撑装置引起机翼上表面激波位置前移(翼梢处除外)，并在机翼翼梢处导致机翼上表面激波结构发生变化。

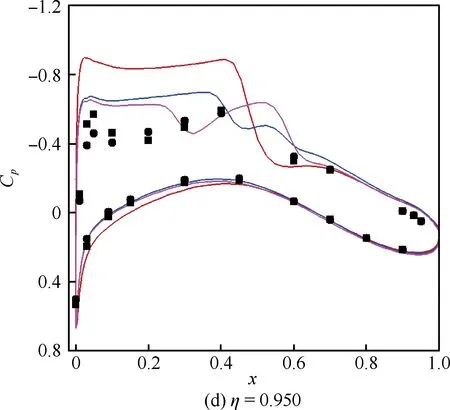
图5 CRM翼身组合体构型典型站位压力系数分布曲线 Fig.5 Curves of pressure coefficients distribution at different spanwise locations of CRM wing-body configuration

3.3 机翼上表面流线 (α=4.0°)

从图4(a)中看出，迎角α=4.0°时，与CRM-WBS-A构型的计算结果不同，采用CRM-WB构型与CRM-WB-A构型得到升力系数均出现明显下降。图6给出了迎角α=4.0°时，采用高阶精度计算方法得到的CRM翼身组合体3种构型的上表面流线，机翼用压力分布着色。由图6可见，迎角α=4.0°时，CRM-WB构型与CRM-WB-A构型升力系数下降是由于翼身结合部后缘分离区突然增加导致的，而CRM-WBS-A构型在翼身结合部后缘则没有明显的分离区。

图6 CRM翼身组合体构型机翼上表面流线(α=4.0°)Fig.6 Streamlines on wing upper surface of CRM wing-body configuration (α=4.0°)

4 结 论

基于5阶空间离散精度的WCNS和SST两方程湍流模型，开展了静气动变形和模型支撑装置对CRM翼身组合体构型气动特性的影响，通过与CRM-WB计算模型和NASA NTF风洞试验结果的对比分析，基本结论如下：

1)α=3.0°时，模型的静气动弹性变形主要导致机翼上表面的激波位置前移及外侧机翼激波位置以前的负压下降。

2)α=3.0°时，模型支撑装置主要导致机翼上表面激波位置前移(翼梢除外)，并使得翼梢位置上表面流动结构发生明显变化。

3)α=4.0°时，计算模型中没有包含支撑装置是导致翼身结合部后缘出现局部分离进而导致升力系数下降的主要原因。

4) 计算模型中同时包含静气动弹性变形和模型支撑装置显著改善了数值模拟结果与试验结果的吻合程度。

致 谢

感谢张玉伦、洪俊武、张书俊和杨小川等同志在高阶精度格式程序实现方面所作的研究工作，感谢中国航空研究院白文博士在数据分析方面提供的帮助。

[1] LEVY D W, VASSBERG J C, WAHLS R A, et al. Summary of data from the First AIAA CFD Drag Prediction Workshop[J]. Journal of Aircraft, 2003, 40(5): 875-882.

[2] LAFLIN K R, VASSBERG J C, WAHLS R A, et al. Summary of data from the Second AIAA CFD Drag Prediction Workshop[J]. Journal of Aircraft, 2005, 42(5): 1165-1178.

[3] VASSBERG J C, TINOCO E N, MANI M, et al. Abridged summary of the Third AIAA CFD Drag Prediction Workshop[J]. Journal of Aircraft, 2008, 45(3): 781-798.

[4] VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the Fourth AIAA Computational Fluid Dynamics Drag Prediction Workshop[J]. Journal of Aircraft, 2014, 51(4): 1070-1089.

[5] VASSBERG J C, DEHAAN M A, RIVERS S M, et al. Development of a common research model for applied CFD validation studies: AIAA-2008-6919[R].Reston, VA: AIAA, 2008.

[6] RIVERS M B, DITTBERNER A. Experimental investigation of the NASA common research model (invited): AIAA-2010-4218[R]. Reston,VA: AIAA, 2010.

[7] RIVERS M B, DITTBEMER A. Experimental investigation of the NASA common research model in the NASA Langley transonic facility and NASA Ames 11-ft transonic wind tunnel (invited): AIAA-2011-1126[R]. Reston, VA: AIAA, 2011.

[8] LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the Fifth Computational Fluid Dynamics Drag Prediction Workshop[J]. Journal of Aircraft, 2014, 51(4): 1194-1213.

[9] 王运涛, 孙岩, 孟德虹, 等. CRM翼身组合体模型高阶精度数值模拟[J]. 航空学报, 2017, 38(3): 120298.

WANG Y T, SUN Y, MENG D H, et al. High-order numerical simulation of CRM wing-body model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120298 (in Chinese).

[10] DAVID H. CFD investigation on the DPW-5 configuration with measured experimental wing twist using the elsA slover and the far-field approach: AIAA-2013-2508[R]. Reston, VA: AIAA, 2013.

[11] KEYE S, BRODERSEN O, RIVERS M B, et al. Investigation of aeroelastic effects on the NASA common research model[J]. Journal of Aircraft, 2014, 51(4): 1323-1330.

[12] TINOCO E N, BRODERSEN O P, KEYE S, et al. Summary of data from the Sixth AIAA CFD Drag Prediction Workshop: CRM case 2 to 5: AIAA-2017-1208[R]. Reston, VA: AIAA, 2017.

[13] RIVERS M B, HUNTER C A, CAMPBELL R L. Further investigation of the support system effects and wing twist on the NASA common research model: AIAA-2012-3209[R]. Reston, VA: AIAA, 2012.

[14] RENDALL T C S, ALLEN C B. Efficient mesh motion using radial basis functions with data reduction algorithms[J]. Journal of Computational Physics, 2009, 228(17): 6231-6249.

[15] SONI B K. Grid generation for internal flow configuration[J]. Computers & Mathematics with Applications, 1992, 24(5-6): 191-201.

[16] 孙岩, 邓小刚, 王运涛, 等. RBF_TFI结构动网格技术在风洞静气动弹性修正中的应用[J]. 工程力学, 2014, 31(10): 228-233.

SUN Y, DENG X G, WANG Y T, et al. Application of structural dynamic grid method based on RBF_TFI on wind tunnel static aero-elastic modification[J]. Engineering Mechanics, 2014, 31(10): 228-233 (in Chinese).

[17] DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 24-44.

[18] DENG X G, MIN R B, MAO M L, et al. Further studies on geometric conservation law and application to high-order finite difference scheme with stationary grid[J]. Journal of Computational Physics, 2013, 239: 90-111.

[19] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[20] CHEN R F, WANG Z J. Fast, Block lower-upper symmetric Gauss-Seidel scheme for arbitrary grids[J]. AIAA Journal, 2000, 38(12): 2238-2245.

[21] 王光学, 张玉伦, 王运涛, 等. BLU-SGS方法在WCNS高阶精度格式上的数值分析[J]. 空气动力学学报, 2015, 33(6): 733-739.

WANG G X, ZHANG Y L, WANG Y T, et al. Numerical analysis of BLU-SGS method in WCNS high-order scheme[J]. Acta Aerodynamica Sinica, 2015, 33(6): 733-739 (in Chinese).