前缘直板扰流对高速空腔的降噪效果分析
2018-04-27周方奇杨党国王显圣刘俊施傲
周方奇,杨党国,*,王显圣,刘俊,施傲
1.中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000 2.中国空气动力研究与发展中心 高速空气动力研究所,绵阳 621000
空腔流动普遍存在于航空航天领域。高速气流流经空腔,当满足一定的空气动力学和几何条件时,腔内流动会产生剧烈的压力脉动并诱发高强度噪声,不仅对空腔流场结构影响较大,而且还威胁腔内设备和空腔自身结构安全。因此针对空腔噪声的抑制研究一直受到广泛关注[1-7],其中前缘扰流流动控制是一种简单有效的噪声抑制方法。Stanek等[8]研究了前缘锯齿、横向圆柱和绕有细铁丝的圆柱杆等扰流装置对腔内流动和噪声的影响。Schmit等[9-11]利用高速摄影技术研究了超声速条件下前缘直板、圆柱和锯齿对腔内流动和噪声的影响,发现前缘扰流装置可以通过抬高剪切层的位置削减进入空腔的流量,从而抑制空腔高强度噪声。Thangamani等[12-14]研究了前缘锯齿对空腔噪声抑制效果,指出前缘锯齿可以改变空腔上方剪切层的三维形态和高度并破坏其连续性。Panickar和Raman[15-16]研究了前缘圆柱对空腔噪声和自持振荡的影响,指出前缘圆柱可以在较大的速度范围内抑制腔内噪声。Dudley和Ukeiley[17-19]发现前缘圆柱可以使剪切层向腔外偏转,从而抬高剪切层的位置并增加其厚度和稳定性,有效减弱与后壁相撞的冲击。国内研究人员也通过在空腔前缘添加锯齿和吹吸气装置等方式,开展了空腔噪声控制研究[20-22]。国内外对空腔流动/噪声的控制研究大多集中在亚声速来流条件下,且关注的重点是对噪声控制效果的分析,而对超声速条件下结合空腔壁面和空间流谱结构的空腔流动/噪声控制研究机理探讨较少。
本文以某型号飞机的工程具体应用为研究背景,通过对比多种不同控制参数状态下腔内的噪声声压级分布,确定前缘直板控制参数的优化选择方法和最优控制参数;综合利用风洞试验测量腔内静态/动态压力、腔壁面油流图谱和流场结构拓扑图,深入分析了跨超声速条件下具有代表性的优选出的典型前缘直板对腔内流动/噪声的控制机理、效果和影响规律,为建立具有工程实用价值的控制对策提供理论支撑和方法借鉴。
1 风洞试验
1.1 试验设备
试验在中国空气动力研究与发展中心高速所的FL-21风洞中完成。FL-21风洞系横截面为 0.6 m×0.6 m半回流暂冲式亚、跨、超三声速风洞,试验马赫数范围为0.2~3.5,试验段长度为 1.775 m。跨声速时试验段上下为槽壁,两侧为实壁,超声速时四壁均为实壁。
利用美国Kulite公司型号为XCE-062的压阻式传感器测量腔内脉动压力,其量程为30 PSI (1 PSI=6.895 kPa),固有频率为200 kHz,试验中传感器采样频率设置为50 kHz。腔内静压则通过PSI 9016电子扫描阀系统进行测量,其量程为15 PSI,测量精度达到±0.05% FS (Full Scale),采样率为每通道100 Hz。
1.2 试验模型
试验模型总长为514 mm,宽为320 mm,腔体的长度L为200 mm,深度D为33.3 mm,宽度W为66.7 mm,长深比为6,宽深比为2。空腔流动控制模型实物如图1所示。
为开展不同类型的试验研究,分别加工了“测压腔”和“油流腔”两种腔体。“测压腔”底部和前壁中轴线上交替分布有脉动压力和静压测点,腔内压力传感器分布如图2所示,其中:x/L为流向坐标与空腔长度的比值。由于模型还需完成后缘修型等其他控制方法的试验研究,有些控制装置需通过空腔后壁的螺孔进行安装,因而后壁面并未布置传感器测点。“油流腔”内部为光滑的金属表面,为了增强油流的对比度,通过电化学的方法使腔体表面黑化(见图1)。

图1 空腔流动控制模型Fig.1 Cavity flow controlling model

图2 腔内压力传感器分布Fig.2 Distoribution of pressure sensors in cavity

图3 空腔前缘处的直板结构Fig.3 Plate structure at leading edge of cavity
空腔前缘设有卡槽用以安装前缘直板扰流装置,与模型前缘之间为200 mm的光滑平板,来流在其上发展形成湍流边界层,并在空腔前缘与直板控制装置相互作用。前缘直板的几何形状通过3个参数确定,分别为展度e、倾斜角度θ和底缝开度h(如图3所示)。来流边界层形态和厚度δ是影响空腔上方剪切层形成、发展和涡脱落频度的一个关键参数,对空腔的流动特征有着重要影响,因而对空腔内的多尺度湍流结构和噪声的控制对策一定要考虑边界层的模拟和影响。为此,依据空腔流动尺度影响和控制技术构建思路,引入前缘直板控制参数e*和h*,分别定义为e*=e/δ,h*=h/δ,代表了前缘直板装置展度e和底缝开度h与空腔前缘来流边界层厚度δ之比,可有效反映空腔前缘直板控制装置尺度与边界层厚度的相对关系以及控制对策的特征参数,指导真实环境和条件下控制措施的构建。
2 数据处理
通过脉动压力传感器采集到的时域信号中包含直流和交流2种成分,经过滤波处理去除直流成分,保留交流成分p(t),其均方根计算式为
(1)
式中:T为样本长度。从而获取脉动压力时域样本的声压级SPL为
(2)
式中:pref=2.0×10-5Pa为参考压力。样本的声压级反映了测点处流场中压力脉动的强度,可以有效描述腔内噪声的分布状况。
利用MATLAB软件函数库中的Pwelch函数计算时域脉动压力样本的功率谱密度PSD,然后通过式(3)获取样本的声压频谱SPFS,从而对腔内噪声进行频谱分析。
(3)
3 控制参数的影响及优化选择
试验中共准备了9种不同控制参数的前缘直板装置,在Ma=0.9和Ma=1.5来流条件下分别开展空腔流动控制试验。根据腔内噪声分布,对比分析展度e、倾斜角度θ和底缝开度h共3种控制参数对控制效果的影响,并确定试验中最优的控制参数和优化选择方法。通过前期的边界层特性测量试验,获取了Ma=0.9和Ma=1.5两种来流条件下空腔前缘处的边界层厚度δ分别为3.3 mm和3.4 mm。利用边界层厚度δ的试验结果和直板的几何尺寸,可以确定Ma=0.9和Ma=1.5来流条件下直板的控制参数e*和h*。
3.1 直板展度的影响
通过对比不同展度前缘直板控制条件下腔内的声压级分布,分析直板展度e对腔内噪声的影响。图4给出了4种不同展度的直板控制条件下腔内壁面中心线上的声压级分布曲线,其中直板的倾角均为45°,底缝开度均为0 mm,展度依次为2.2、3.3、4.4和5.5 mm,具体的参数见表1。通过图4中声压级曲线的对比可以看出:在倾角和底缝开度不变的情况下,随着直板展度的增加,腔内声压级逐渐降低,其中Ma=0.9时声压级的变化主要集中在空腔的两端,中段变化相对微弱;Ma=1.5时则表现为声压级曲线整体向下平移。另外,直板展度从2.2 mm增加至3.3 mm时声压级下降的幅度最大,在后缘测点处Ma=0.9和Ma=1.5时分别达1.3 dB和1.2 dB,展度继续增加后声压级降低的幅值逐渐减小。上述现象表明:当e<3.3 mm,e*<1.0时,即前缘直板的展度小于来流边界层厚度时,腔内噪声对展度的变化较敏感,直板展度的增加对噪声抑制具有较强的效果;当展度大于边界层厚度时,腔内噪声对展度的敏感性逐渐减弱。

图4 不同展度的直板控制条件下腔内声压级分布Fig.4 Distribution of sound pressure level in cavity for controlling with plates of different extents
表1 不同展度直板的具体参数Table 1 Parameters of plates with different extents

Platee/mmθ/(°)h/mme*Ma=0.9Ma=1.5Plate-12.24500.670.64Plate-23.34501.000.97Plate-34.44501.331.29Plate-45.54501.671.62
直板展度的增加虽然可以降低腔内噪声,但同时也会增大直板在来流法向上的投影面积,导致空腔附近阻力的提升,进而影响飞行器的整机气动特性和飞行性能。因而结合噪声抑制效果和气动特性需求,前缘直板的展度与边界层厚度相当(本试验中为3.3 mm左右)时应用价值最大。
3.2 直板倾角的影响
直板的倾角主要是依据超声速来流条件下空腔前缘产生的典型流动特征(如膨胀波或激波等)的倾斜角度来确定的。通过对比不同倾角前缘直板条件下腔内的声压级分布,分析直板倾角对腔内噪声的影响。图5给出了3种不同倾角的直板控制条件下腔内的声压级分布曲线,其中直板的展度均为3.3 mm,与来流边界层厚度基本相当,底缝开度均为0 mm,倾角θ依次为30°、45°和60°,具体的参数见表2。从图5中不同曲线间的对比可以看出:在直板展度和底缝开度不变的情况下,当倾角从30°增长到45°时,Ma=0.9条件下后缘附近声压级显著下降,Ma=1.5条件下声压级曲线整体向下平移;当倾角从45°增大到60°,Ma=0.9条件下大部分区域声压级变化微弱,而Ma=1.5条件下两条声压级曲线几乎重合。上述现象表明:当前缘直板的倾角θ<45°时,腔内噪声对直板倾角的变化比较敏感,倾角的增加有利于对腔内噪声的抑制;当倾角θ>45°时,继续增大倾角对腔内噪声影响微弱。另外,倾角的增大也会增加直板在来流法向上的投影面积,提高空腔附近的阻力,因而综合考虑噪声抑制和气动特性需求,空腔前缘直板控制的最优倾角为45°。
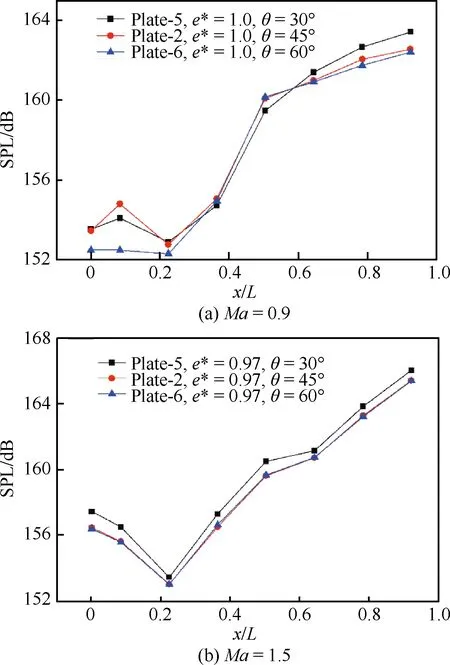
图5 不同倾角的直板控制条件下腔内声压级分布Fig.5 Distribution of sound pressure level in cavity for controlling with plates of different angles
表2 不同倾角直板的具体参数Table 2 Parameters of plates with different angles
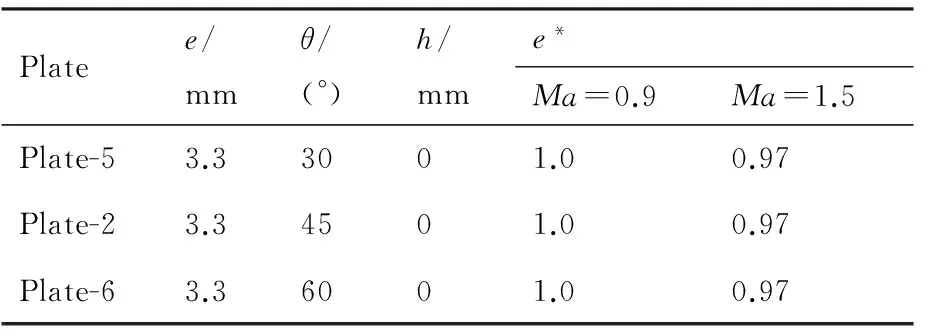
Platee/mmθ/(°)h/mme*Ma=0.9Ma=1.5Plate-53.33001.00.97Plate-23.34501.00.97Plate-63.36001.00.97
3.3 直板底缝开度的影响
通过对比不同底缝开度前缘直板条件下腔内的声压级分布,分析直板底缝对腔内噪声的影响。图6给出了4种不同底缝开度的直板控制条件下腔内声压级分布,4种直板的展度均为3.3 mm,倾角θ均为45°,底缝开度依次为0、0.5、1.0和1.5 mm,具体参数见表3。从图6中可以看出:当直板展度和倾角不变时,随着直板底缝开度的增加,除Ma=0.9条件下个别测点外,腔内声压级均逐渐减小。通过声压级曲线的变化趋势可以发现:当h<1 mm,h*<0.3时,腔内声压级对底缝开度的变化较敏感,随着底缝开度的增加,后部声压级显著下降,底缝开度h从0.5 mm增加到1.0 mm时,Ma=0.9和Ma=1.5条件下后缘声压级降低幅值均达到0.7 dB以上;当h>1 mm,h*>0.3时,虽然噪声对开度的敏感性减弱,增加底缝开度仍然可以使得声压级继续下降。上述现象表明在试验提供的底缝开度变化范围内,即h≤1.5 mm条件下,通过在前缘直板的底部增加底缝可以增强对腔内噪声的抑制,底缝开度的增大可以提升噪声的抑制效果。另外,由于底缝开度变化的过程中直板在来流法向上的投影面积保持不变,对飞行器的气动特性影响较小。因而增加底缝开度有利于直板对空腔噪声的抑制,试验提供的底缝开度最大值h=1.5 mm为最优底缝开度。

图6 不同底缝开度直板控制条件下腔内声压级分布Fig.6 Distribution of sound pressure level in cavity for controlling with plates of different crack sizes
表3 不同底缝开度直板的具体参数Table 3 Parameters of plates with different crack sizes

Platee/mmθ/(°)h/mmh*Ma=0.9Ma=1.5Plate-23.345000Plate-73.3450.50.150.147Plate-83.3451.00.300.290Plate-93.3451.50.450.440
通过以上9种前缘直板控制条件下腔内声压级的分类对比,分别对前缘直板的展度、倾角和底缝开度3个控制参数进行了优化选择,并确定了试验中的最优控制参数:展度e=3.3 mm,倾角θ=45°,底缝开度h=1.5 mm。而前缘直板Plate-9的展度、倾角和底缝开度均与3种最优控制参数相符,同时在其作用下腔内声压级也低于其他流动控制状态,因而第4节将以直板Plate-9为研究对象,对前缘直板流动控制条件下腔内的流场和噪声进行深入分析。
4 典型前缘直板控制效果分析
开展Ma=0.9和Ma=1.5来流条件下的风洞试验,根据无流动控制的基准状态及前缘直板Plate-9流动控制状态下腔内静态/动态压力测量和壁面油流试验结果,分析前缘直板Plate-9对腔内流场和噪声特性的影响规律和控制机理。
4.1 静压分布
利用壁面的静压测点可以获取不同来流条件下腔内流场的静压分布,基准状态和前缘直板Plate-9流动控制状态下腔内底面中轴线上无量纲静压系数Cp的分布曲线如图7所示,从中可以看出:无论在Ma=0.9还是Ma=1.5来流条件下,基准状态时Cp曲线均呈明显的3段式拟线性分布,因此可以根据该特征将腔内流场沿流向划分为3个区域:Ⅰ区域x/L∈(0,0.43)、Ⅱ区域x/L∈[0.43,0.85)和Ⅲ区域x/L∈[0.85,1.00),并从以上3个区域分别分析前缘直板对腔内静压的影响。

图7 基准状态和Plate-9流动控制条件下腔内 无量纲静压分布 Fig.7 Distribution of dimensionless static pressure in cavity under basic and Plate-9 flow controlling conditions
对比基准状态和流动控制状态下的Cp曲线,发现在空腔前缘安装直板Plate-9后,腔内3个区域静压系数均有所下降,其中:Ⅲ区域中的变化最为显著,Ma=0.9和Ma=1.5条件下后缘附近Cp分别降低0.394和0.258;而Ⅰ区域中控制效果相对较弱,表现为曲线整体向下平移,Ma=0.9和Ma=1.5时分别下移幅度约0.1和0.05左右。另外,前缘直板还改变了Ⅱ区域中静压的发展趋势,使得压力最低点的位置发生变化,不同来流条件下腔内静压的最低点均由基准状态时的x/L=0.42附近移至x/L=0.71,同时Ⅱ区域中Cp曲线变化趋势也随之改变,由基准状态时的线性增加,转变为先减小后增大。腔内静压的变化状况说明前缘直板流动控制主要对Ⅲ区域中产生较大作用,并引起Ⅱ区域流场结构的改变,而对前部Ⅰ区域影响相对较弱。
4.2 油流图谱
油流图谱代表了壁面的摩擦力线分布情况,可以有效反映流体在壁面的分离和附着特征,以及附近流场结构,因而通过对比前缘直板Plate-9流动控制前后空腔壁面流谱,可以进一步分析前缘直板对腔内流场的影响。图8和图9分别给出了Ma=0.9和Ma=1.5来流条件下基准状态和流动控制状态腔内各壁面的油流图谱照片。
侧壁照片中空腔上缘处的横向轨迹反映了剪切层的发展状况。从图8(a)和图9(a)中可以看出:Ma=0.9和Ma=1.5时,基准状态条件下剪切层均从前缘附近产生并沿空腔上缘向后运动,在此过程中其厚度逐渐增长并向腔内延伸,其中亚声速条件下剪切层厚度的增长率高于超声速。而流动控制状态下,空腔侧壁上缘附近基本无横向轨迹,流谱主要呈纵向分布,与基准状态时的表现差异较大,这是由于前缘倾斜的直板装置不仅抬高了剪切层分离点的位置,同时增强了流体向腔外的速度分量,导致剪切层的运动高度大幅度上升并从腔外掠过,因而侧壁的流谱中难以观察到其流动轨迹。
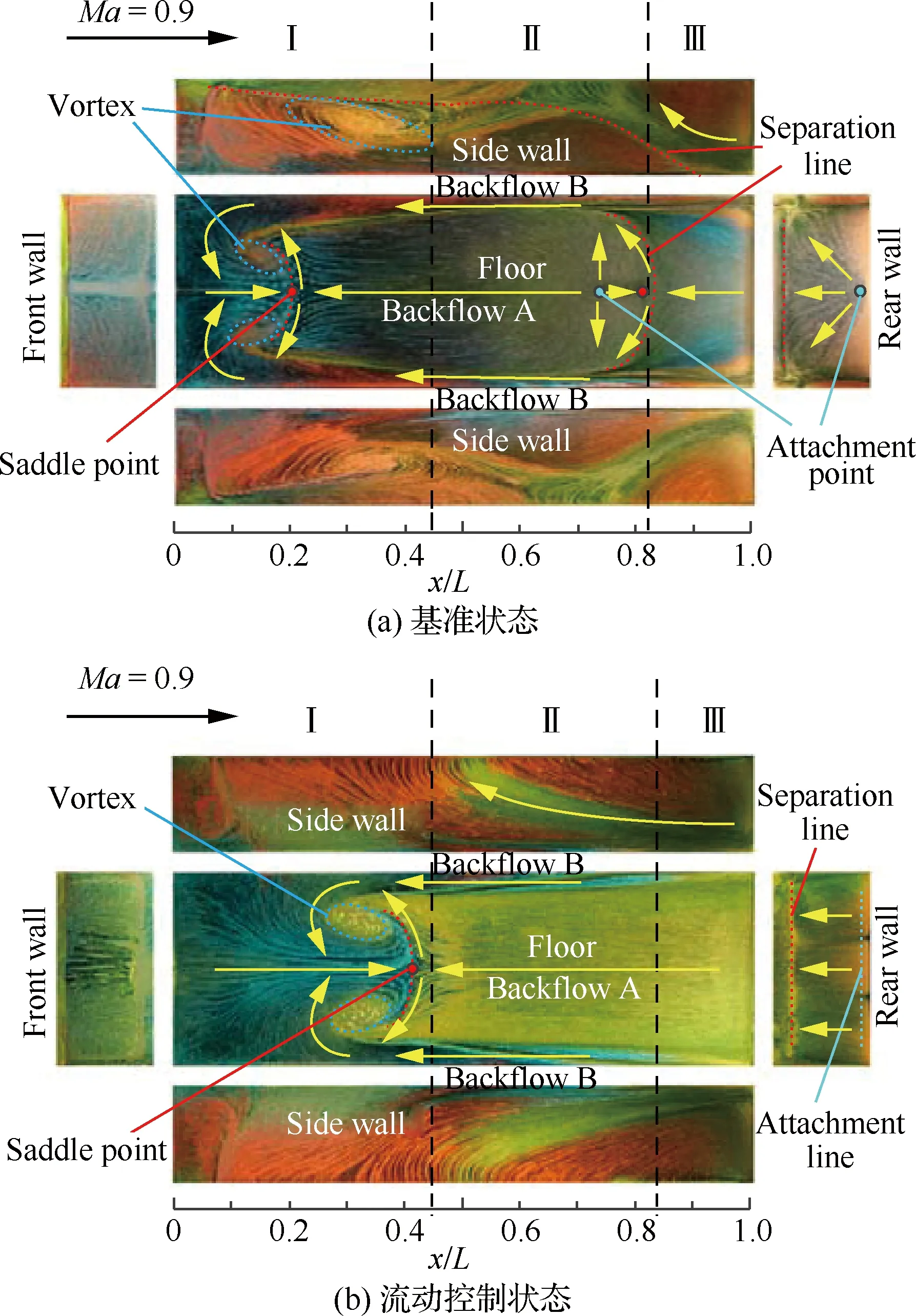
图8 Ma=0.9时基准状态和直板Plate-9流动 控制条件下空腔壁面油流图谱 Fig.8 Oil flow patterns on cavity surfaces under basic condition and Plate-9 flow controlling conditions at Ma=0.9

图9 Ma=1.5时基准状态和直板Plate-9流动 控制条件下空腔壁面油流图谱 Fig.9 Oil flow patterns on cavity surfaces under basic condition and Plate-9 flow controlling conditions at Ma=1.5
剪切层的抬升导致流体对后缘的撞击位置发生改变。基准状态下剪切层沿流向运动过程中,在到达后壁之前已接触底面,图8(a)和图9(a)中底面和后壁上附着点的位置说明流向流体撞击范围从底面后部延伸至后壁。而在流动控制状态下,由于剪切层位置的上升以及向腔外速度分量的增加,流体的横向运动距离增大,在后缘的撞击位置也向后推移,从图8(b)和图9(b)可以看出流体在后缘的附着区域主要集中在空腔后壁面,与基准状态相比流体的撞击范围显著缩小,从而进入腔内的流量也随之减少。
撞击空腔后缘后,流体沿底面向前回流。根据底面流谱中横向轨迹的颜色,可将回流分为两部分:回流A沿底面中轴线向前运动,直至Ⅰ区域中的分离线,其流动轨迹集中在底面中轴线及其两侧;回流B则沿两侧壁向前缘流动,在Ⅰ区域中撞击前壁后改变方向,向底面中轴线汇聚同时转为沿流向流动。通过Ⅱ区域底面照片可以看出回流A流谱轨迹的截面宽度远大于回流B,说明回流A的流量远多于回流B,为腔内的主要回流。
Ma=0.9来流条件下,两部分回流在Ⅰ区域相撞并发生流动分离,底面图谱中可以清晰地看见两者交汇形成的鞍点、分离线以及沿中轴线对称的两个旋涡分离点。基准状态下剪切层在后缘的撞击范围较大,底面回流强度也较高,回流A的流量远多于回流B,因而Ⅰ区域中两部分流体相撞产生的鞍点和分离线的位置趋于前壁,位于x/L=0.2左右(见图8(a))。而在流动控制状态下,从后缘进入腔内的流量减少,导致回流A的强度显著下降,因而底面鞍点和分离线向右移动,从x/L=0.2右移至x/L=0.4附近(见图8(b))。
Ma=1.5时,基准状态条件下空腔底面油流图谱与Ma=0.9时类似(见图9(a)),流动控制状态下,Ⅰ区域中沿中轴线对称的分离线和两个旋涡分离点被一个旋涡分离点取代(见图9(b)),回流A和回流B共同汇入该分离点,使得底面流谱表现出一定的非对称性。超声速条件下来流的非稳定性较强,而前缘直板又进一步放大了流动的非稳定性,从而引起两侧回流B的失衡,在前壁附近汇聚的过程中偏离了中轴线,因而在Ⅰ区域与回流A的撞击并不充分,两者在交汇过程中形成一个距离前壁较近的旋涡分离点。
4.3 流场结构
根据油流图谱中底面流动分离和附着的位置以及侧壁旋涡的形态定性描绘了Ma=0.9和Ma=1.5条件下腔内中轴面上的流场结构,如图10和图11所示。
基准状态下剪切层在发展过程中厚度逐渐增加,最终撞击空腔底面和后壁,形成后缘高压和沿底面向前的回流,以及横跨Ⅰ和Ⅱ区域的主回流旋涡(图8(a)和图9(a)底面照片中Ⅰ区域的分离线反映了回流区的范围);流动控制状态下,前缘直板有效地抬高了剪切层,增加了其流向的运动距离,使得部分流体直接跨过空腔,从而降低了流体进入腔内的流量,以及对后缘的撞击强度。
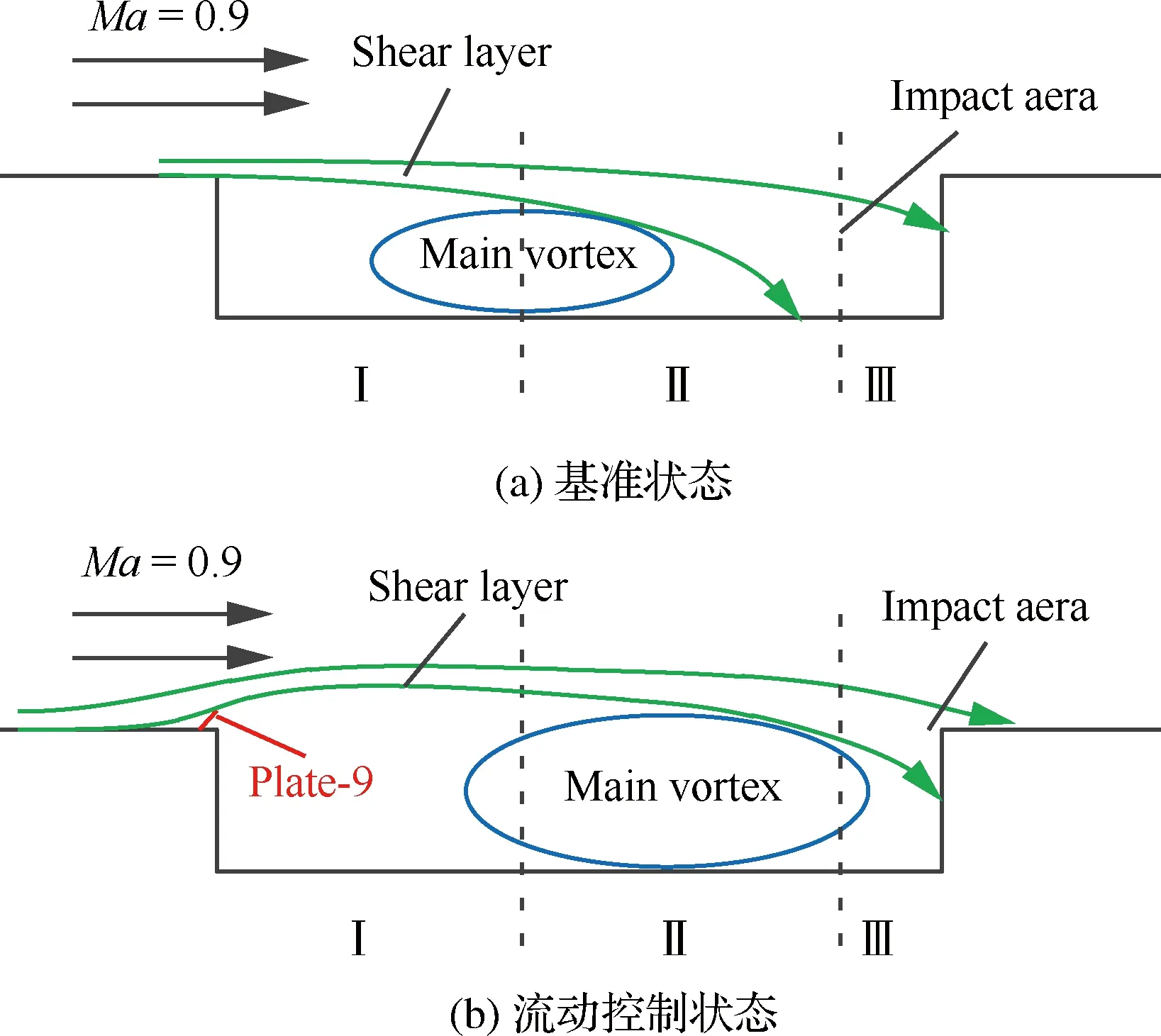
图10 Ma=0.9时腔内流向中轴面流场结构Fig.10 Flow configuration on axis surface of cavity at Ma=0.9

图11 Ma=1.5时腔内流向中轴面流场结构Fig.11 Flow configuration on axis surface of cavity at Ma=1.5
通过对剪切层的抬高作用,前缘直板不仅降低了腔内静压和后缘逆压梯度(见图7),同时削弱了腔内回流的强度,抑制了回流区的范围。Ma=0.9时底面Ⅰ区域的分离线在前缘直板的作用下从x/L=0.2附近移动至x/L=0.4(见图8),反映了主回流旋涡的后移。另外,主旋涡中心压力较低,在Ⅱ区域的流场中形成压力最低点,而随着主回流旋涡的后移,底面静压最低点的位置也随之向右移动,图7中压力最低点位置与图10和图11中主回流旋涡中心保持一致。
4.4 腔内声压级
腔内的复杂流动会产生剧烈的压力脉动,从而形成高强度噪声,利用脉动压力传感器的测量结果,对腔内噪声的分布特性进行分析。图12给出了Ma=0.9和Ma=1.5来流条件下腔内总声压级的分布曲线,可以看出基准状态下腔内声压级沿流向均成波浪式上升分布,并在空腔后缘分别达到最大值172.27 dB和172.13 dB。

图12 基准状态和直板Plate-9流动控制条件下 腔内声压级分布曲线 Fig.12 Curves of sound pressure level in cavity under basic conditions and Plate-9 flow controlling conditions
在空腔前缘安装直板Plate-9后,腔内噪声得到有效抑制,尤其在空腔中后部分声压级显著下降,Ma=0.9和Ma=1.5来流条件下后缘附近声压级降低幅值分别达11.13 dB和8.0 dB。在前缘直板流动控制条件下,剪切层被大幅度抬高,有效减弱了流体撞击后缘时的强度和流量,从而抑制了后缘高强度噪声的产生。
4.5 声压频谱
空腔后缘附近声压级最强,且前缘直板Plate-9对后缘处噪声的抑制效果也十分显著,因此通过后缘测点的声压频谱进一步分析腔内噪声的特性。图13对比了基准状态和流动控制状态下后缘附近x/L=0.92处的声压频谱。根据频谱曲线的峰值确定腔内噪声的模态频率,并利用蓝色虚线在图13中对其位置进行了标注,可以看出在Ma=0.9和Ma=1.5条件下基准状态和流动控制时峰值位置保持一致,说明前缘直板对腔内噪声的模态频率基本无影响。
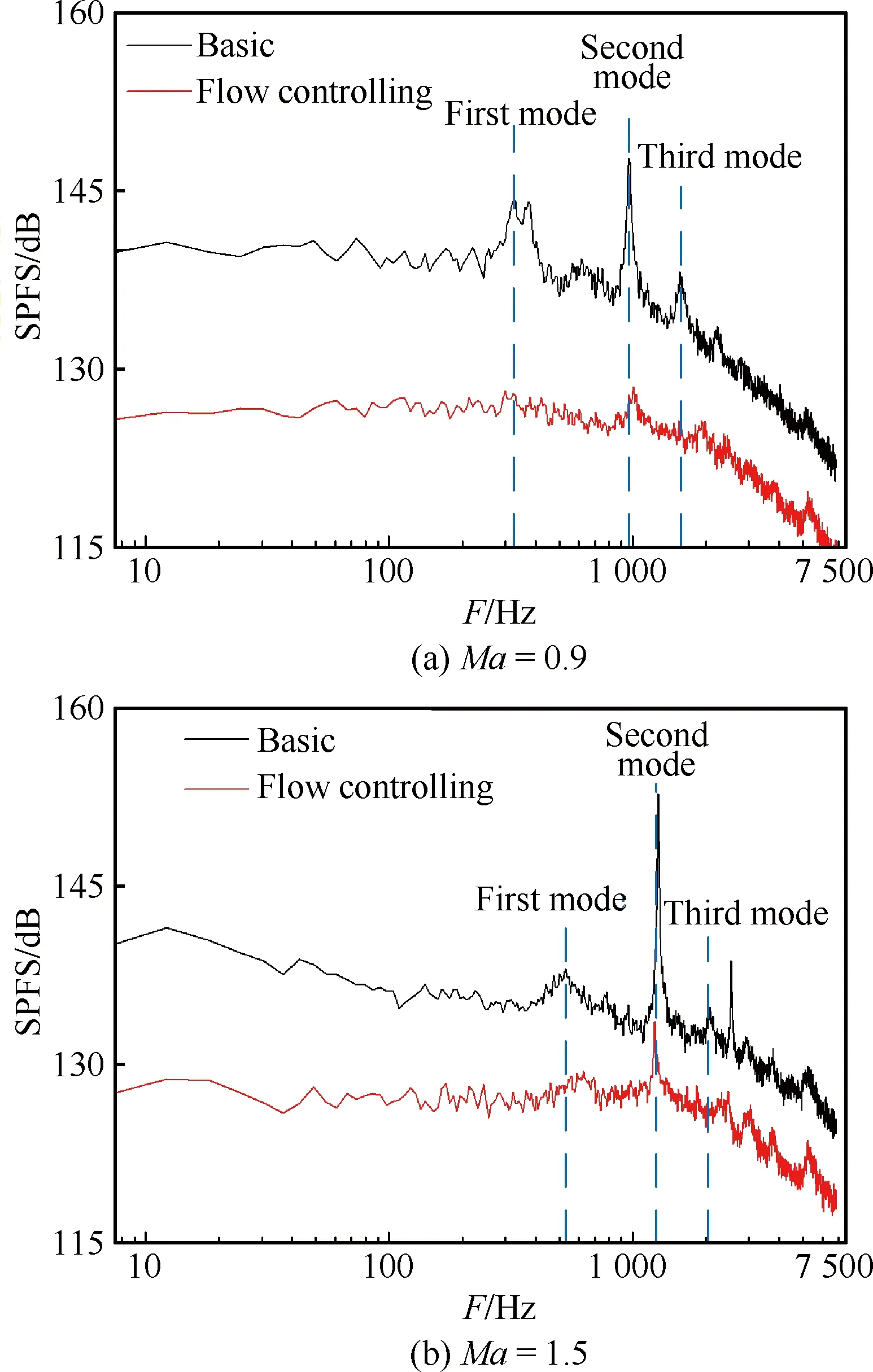
图13 空腔后缘附近测点处的声压频谱Fig.13 Sound pressure level spectra of aft edge in cavity
在空腔前缘安装直板Plate-9之后,无论是亚声速还是超声速条件下,声压频谱曲线显著向下平移,宽频噪声和峰值噪声都受到显著影响。在前缘直板的作用下,宽频噪声在低频范围内(小于1 000 Hz)受到明显的抑制,该效果随着频率的增加逐渐减弱;同时,腔内峰值噪声的幅值也大幅度降低,尤其是最高峰值(二阶模态峰值),在Ma=0.9和Ma=1.5来流条件下分别下降了19.4 dB和22.5 dB。
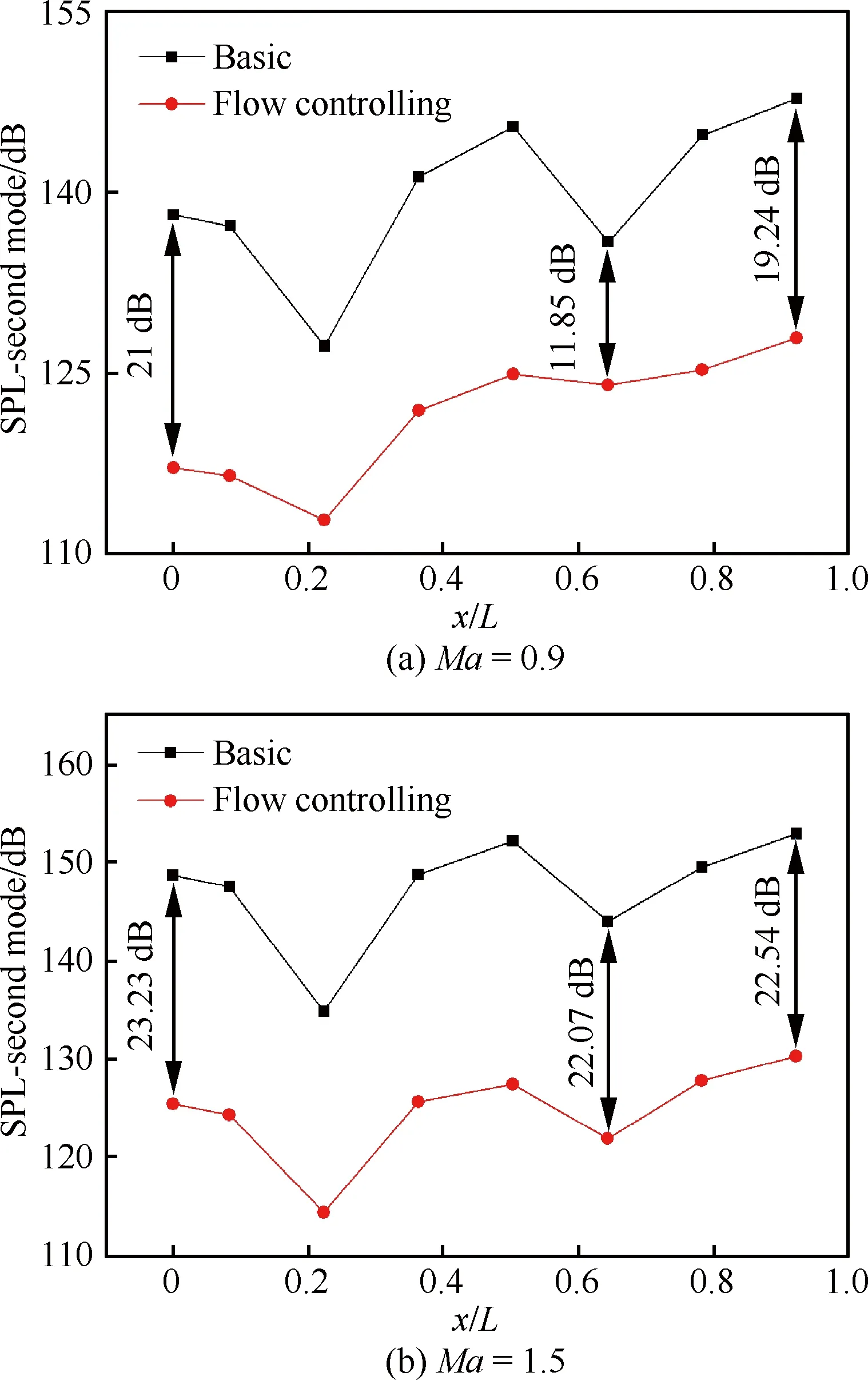
图14 基准状态和直板Plate-9流动条件下腔内 二阶模态噪声空间分布曲线 Fig.14 Curves of spatial distribution of the second mode noise in cavity under basic and Plate-9 flow controlling conditions
为进一步分析前缘直板对腔内峰值噪声的影响,图14给出了不同Ma条件下腔内二阶模态峰值噪声幅值在底面的分布曲线。基准状态条件下峰值噪声在腔内呈波浪式分布,而在前缘安装直板Plate-9之后,峰值噪声的幅值曲线整体向下平移,Ma=0.9和Ma=1.5时分别降低11 dB和20 dB以上,表明前缘直板对峰值噪声的抑制效果在整个空腔内均十分显著。峰值噪声产生于剪切层中非定常运动对后缘的周期性撞击,并以压力波的形式在腔内传播。由于前后壁面的多次反射,压力波在腔内叠加形成驻波,因而其幅值在空间上呈波浪式分布。前缘直板抬高了剪切层的高度,并削弱了其对后缘的撞击作用,从声源上抑制了峰值噪声的产生,减小了腔内压力波的强度和驻波的幅值,从而使得峰值噪声的幅值在整个腔内大幅度下降。
5 结 论
1) 在前缘直板的作用下,剪切层的位置大幅度抬高,导致与腔后缘的撞击位置显著后移,从而削弱流体进入空腔的流量及对后缘的撞击强度。
2) 前缘直板通过减少进入腔内的流量降低了腔内静压和前后缘的压差,抑制了回流的强度和范围,并导致回流旋涡和静压低点向下游移动。
3) 前缘直板通过削弱剪切层对后缘的撞击强度,有效降低了空腔后壁处的噪声源强度,进而实现了空腔内声压级的控制,不仅使激振频率处的峰值噪声大幅度下降,还使宽频噪声也受到明显抑制。
[1] FLAHERTY W, REEDY T M, GREGORY S, et al. Investigation of cavity flow using fast-response pressure sensitive paint[C]∥51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston, VA: AIAA, 2013: 1-15.
[2] THIEMANN C L, MILNE G J, VAKILI A D. An experimental investigation of supersonic cavity flow control with vertical cylinders[C]∥43rd Fluid Dynamics Conference. Reston, VA: AIAA, 2013: 1-13.
[3] GUPTA A D, ROY S. Noise control of cavity flows for subsonic receptive channels[C]∥53rd AIAA Aerospace Sciences Meeting. Reston, VA: AIAA, 2015: 1-10.
[4] SHAABAN M, MOHANY A. Passive control of flow excited acoustic resonance in rectangular cavities using upstream mounted blocks[J]. Experiments in Fluids, 2015, 56(72): 1-12.
[5] ALHADDABI N, KONTIS K, ZARE-BEHTASH H. Control of low-speed cavity flow using steady jets[C]∥8th AIAA Flow Control Conference. Reston, VA: AIAA, 2016: 1-13.
[6] 杨党国, 范召林, 李建强, 等. 后壁倒角对空腔噪声的抑制效果[J]. 实验流体力学, 2010, 24(5): 22-25.
YANG D G, FAN Z L, LI J Q, et al. Suppression effect of rear-face angle of cavity on aerodynamic noise[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(5): 22-25 (in Chinses).
[7] 宁方立, 史红兵, 丘廉芳, 等. 前缘高频振动对亚声速开式空腔内强噪声影响的数值研究[J]. 航空学报, 2015, 36(12): 3843-3852.
NING F L, SHI H B, QIU L F, et al. Numerical research of high frequency vibration effect on subsonic open cavity macro-noise[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3843-3852 (in Chinese).
[8] STANEK M J, RAMAN G, ROSS J, et al. High frequency acoustic suppression-the role of mass flow, the notion of superposition, and the role of inviscid instability-a new model (Part II)[C]∥8th AIAA/CEAS Aeroacoustics Conference & Exhibit. Reston, VA: AIAA, 2002: 1-30.
[9] SCHMIT R F, MCGAHA C, TEKELL J, et al. Performance results for the optical turbulence reduction cavity[C]∥47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston, VA: AIAA, 2009: 1-13.
[10] SCHMIT R F, SEMMELMAYER F, HAVERKAMP M, et al. Analysis of cavity passive flow control using high speed shadowgraph image[C]∥47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston, VA: AIAA, 2009: 1-13.
[11] SCHMIT R F, SEMMELMAYER F, HAVERKAMP M, et al. Examining passive flow control devices with high speed shadowgraph images around a Mach 1.5 cavity flow field[C]∥6th AIAA Flow Control Conference. Reston, VA: AIAA, 2013: 1-19.
[12] THANGAMANI V, KNOWLES K, SADDINGTON A J. The effects of scaling on high subsonic cavity flow oscillations and control[C]∥18th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2012: 1-16.
[13] THANGAMANI V, KNOWLES K, SADDINGTON A J. An investigation of passive control methods for a large scale cavity model in high subsonic flow[C]∥19th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2013: 1-13.
[14] SADDINGTON A J, KNOWLES K, THANGAMANIET V, et al. Scale effects on the performance of sawtooth spoilers in transonic rectangular cavity flow[J]. Experiments in Fluids, 2016, 57(2): 1-12.
[15] PANICKAR P, RAMAN G. Understanding the mechanism of cavity resonance suppression using a cylindrical rod in cross-flow[C]∥46th AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2008: 1-27.
[16] PANICKAR P, RAMAN G. Cavity resonance suppression using high frequency excitation the mystery of the cylinder in crossflow revisited[C]∥14th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2008: 1-24.
[17] DUDLEY J G, UKEILEY L. Suppression of fluctuating surface pressures in a supersonic cavity flow[C]∥5th Flow Control Conference. Reston, VA: AIAA, 2010: 1-22.
[18] DUDLEY J G, UKEILEY L. Detached eddy simulation of a supersonic cavity flow with and without passive flow control[C]∥20th AIAA Computational Fluid Dynamics Conference. Reston, VA: AIAA, 2011: 1-18.
[19] DUDLEY J G, UKEILEY L. Passively controlled supersonic cavity flow using a spanwise cylinder[J]. Experiments in Fluids, 2014, 55(9): 1-22.
[20] 杨党国, 吴继飞, 罗新福. 零质量射流对开式空腔气动噪声抑制效果分析[J]. 航空学报, 2011, 32(6): 1107-1114.
YANG D G, WU J F, LUO X F. Investigation on suppression effect of zero-net-mass-flux jet on aerodynamic noise inside open cavities[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1107-1114 (in Chinses).
[21] 吴亚东, 欧阳华, 黄友. 基于被动控制的空腔脉动压力实验研究[J]. 工程热物理学报, 2013, 34(9): 1640-1644.
WU Y D, OUYANG H, HUANG Y. Experimental investigation on the fluctuating pressure of cavity based on passive controls[J]. Journal of Engineering Thermophysics, 2013, 34(9): 1640-1644 (in Chinese).
[22] 吴继飞, 徐来武, 范召林, 等. 开式空腔气动声学特性及其流动控制方法[J]. 航空学报, 2015, 36(7): 2015-2165.
WU J F, XU L W, FAN Z L, et al. Aeronautica characteristics and flow control method of open cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2015-2165 (in Chinese).
