从一题多解走向多题归一

刘韩

深度和广度是思维的两个特性，培养学生思维的广度要强化一题多解，重视一题多变。训练学生思维的深度要培养学生追根溯源的习慣，强调多解归一，并注重知识的系统性。从思维的发展来看，二者维度不同，方向不一，但从知识形成的过程来看，二者相辅相成，不可割裂。思维的广度和深度之间有着怎样的联系呢？

拓展思维的广度，强化一题多解，达到熟练

在人教版四年级下册“数学广角”鸡兔同笼问题的教学中，有这样一道例题：

笼子里有若干只鸡、兔。从上面数，有8个头，从下面数，有26只脚，鸡和兔各有几只？

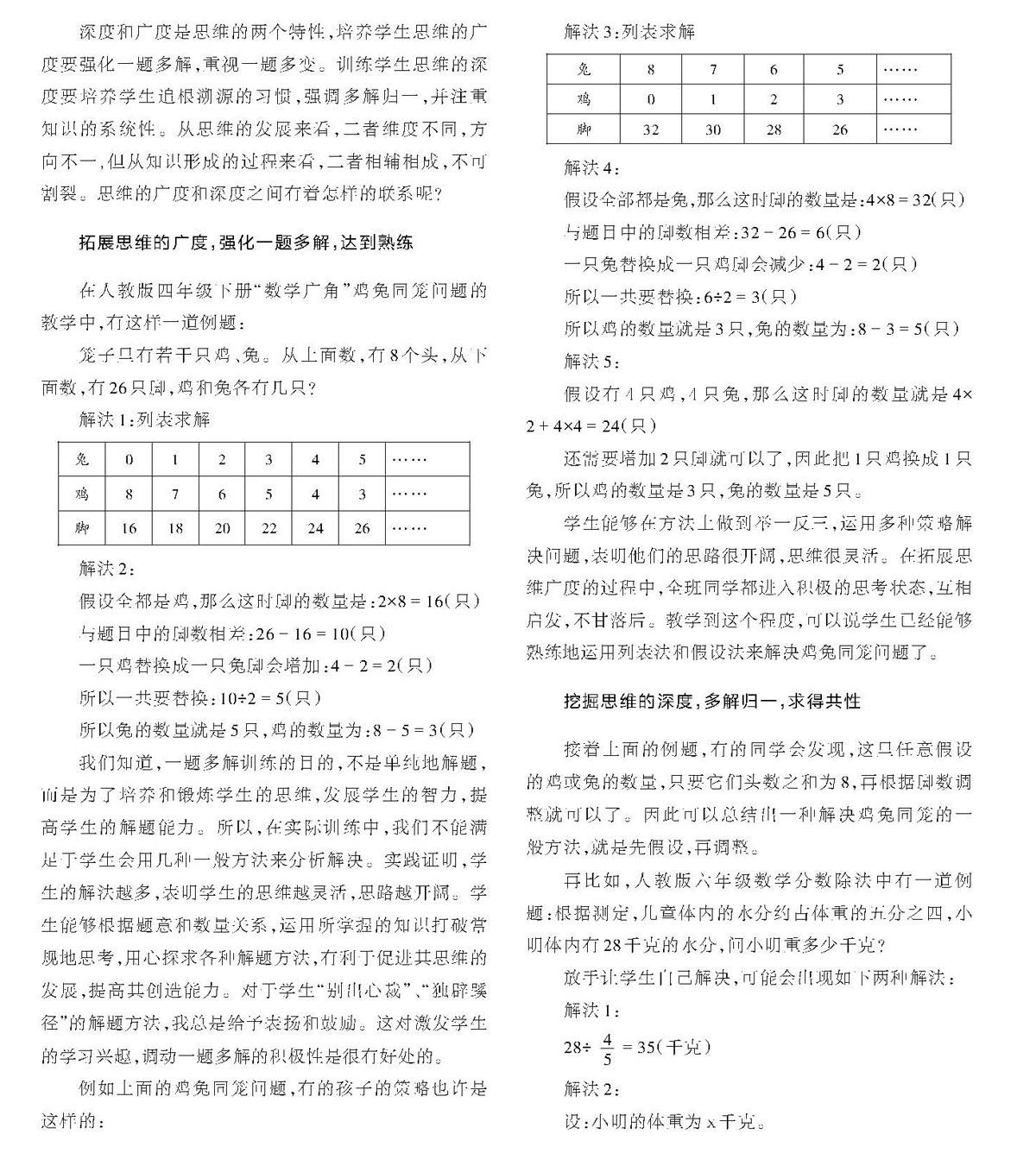
解法1：列表求解

解法2：

假设全都是鸡，那么这时脚的数量是：2×8=16（只）

与题目中的脚数相差：26-16=10（只）

一只鸡替换成一只兔脚会增加：4-2=2（只）

所以一共要替换：10÷2=5（只）

所以兔的数量就是5只，鸡的数量为：8-5=3（只）

我们知道，一题多解训练的目的，不是单纯地解题，而是为了培养和锻炼学生的思维，发展学生的智力，提高学生的解题能力。所以，在实际训练中，我们不能满足于学生会用几种一般方法来分析解决。实践证明，学生的解法越多，表明学生的思维越灵活，思路越开阔。学生能够根据题意和数量关系，运用所掌握的知识打破常规地思考，用心探求各种解题方法，有利于促进其思维的发展，提高其创造能力。对于学生“别出心裁”、“独辟蹊径”的解题方法，我总是给予表扬和鼓励。这对激发学生的学习兴趣，调动一题多解的积极性是很有好处的。

例如上面的鸡兔同笼问题，有的孩子的策略也许是这样的：

解法3：列表求解

解法4：

假设全部都是兔，那么这时脚的数量是：4×8=32（只）

与题目中的脚数相差：32-26=6（只）

一只兔替换成一只鸡脚会减少：4-2=2（只）

所以一共要替换：6÷2=3（只）

所以鸡的数量就是3只，兔的数量为：8-3=5（只）

解法5：

假设有4只鸡，4只兔，那么这时脚的数量就是4×2+4×4=24（只）

还需要增加2只脚就可以了，因此把1只鸡换成1只兔，所以鸡的数量是3只，兔的数量是5只。

学生能够在方法上做到举一反三，运用多种策略解决问题，表明他们的思路很开阔，思维很灵活。在拓展思维广度的过程中，全班同学都进入积极的思考状态，互相启发，不甘落后。教学到这个程度，可以说学生已经能够熟练地运用列表法和假设法来解决鸡兔同笼问题了。

挖掘思维的深度，多解归一，求得共性

接着上面的例题，有的同学会发现，这里任意假设的鸡或兔的数量，只要它们头数之和为8，再根据脚数调整就可以了。因此可以总结出一种解决鸡兔同笼的一般方法，就是先假设，再调整。

再比如，人教版六年级数学分数除法中有一道例题：根据测定，儿童体内的水分约占体重的五分之四，小明体内有28千克的水分，问小明重多少千克？

放手让学生自己解决，可能会出现如下两种解法：

解法1：

28÷ [45]=35（千克）

解法2：

设：小明的体重为x千克。

[45]x=28

x=35

解法1是利用算式计算，解法2利用了方程。如果问为什么用28÷[45]就是小明的体重呢？列算式的同学会解释说，因为根据题意可以得出，小明的体重×[45]=小明体内的水分，那么小明体内的水分÷[45]=小明的体重。同样的，如果问为什么设小明的体重为x千克，那么就可以列方程[45]x=28呢？此时列方程的同学也会解释说，根据题意，小明的体重×[45]=小明体内的水分，这里小明的体重是未知，小明体内的水分是已知，所以可以根据这个等量关系来设未知数列方程。看来两种方法的共同点都是使用了“小明的体重×[45]=小明体内的水分”这个等量关系式。从而发现，不管是列算式，还是列方程，解决这个问题的关键都在于分析题目中的数量关系。

与追求一题多解相比，有经验的教师往往会引导学生思考“多解归一”，即这个问题为什么会有不同的解法，这些不同的思路之间存在着怎样的共同点，并在此基础上揭示出问题的深层结构，从而得到一般性的方法。多坚持这样的训练，学生就会形成“解一题，通一类，连一片”的思维。

提升思维的灵活性，在多题归一中寻找规律

人教版五年级数学上册的“数学广角”植树问题中，有道习题是这样的：一张桌子坐6人，两张桌子并起来坐10人，三张桌子并起来坐14人……照这样，10张桌子并成一排可以坐多少人？乍一看，这道题跟植树问题好像风马牛不相及，为何会出现在植树问题的课后习题中呢？这就要从例题说起。

例1：同学们在全长100m的小路一边植树，每隔5m栽一棵（两端要栽），一共要栽多少棵树？

分析：100m太长，我们可以用简单数来试试。

假设只有20m，5m一个间隔，一共有4个间隔，通过画图，我们发现需要栽5棵树。

如果是25m，5m一个间隔，一共有5个间隔，通过画图，我们发现需要栽6棵树。

进而发现栽树的棵树和间隔数之间有着一定的联系。再经过思考和论证，发现两端都栽，栽树的棵数就比间隔数多1。

列式：100÷5=20

有20个间隔，两端都要栽，所以一共要栽21棵树。

例2：大象馆和猴山相距60m，绿化队要在两馆间的小路两旁栽树（两端不栽），相邻两棵树之间的距离是3m。一共要栽多少棵？

分析：由于两端不栽，棵树与段数的关系跟例1可能会不同。全长60m，3m一个间隔，一共有20个间隔，数据比较大，因此我们还是可以先将大数据化为小数据试一试。如果只有3个间隔，通过画图我们发现要栽2棵树。如果是4个间隔，那么就需要栽3棵树。经过思考发现两端都不栽，栽的棵数比间隔数少1，所以这里20个间隔，一边就要栽19棵，两边就是19×2=38（棵）。

例3：张伯伯准备在圆形池塘周围栽树，池塘的周长是120m，如果每隔10m栽一棵，一共要栽多少棵树？

分析：继续研究棵树与段数之间的关系，如果周长是40米，4个间隔，通过画图发现能栽4棵树。再举例，如果周长是30米，3个间隔，那么能栽3棵树。经过思考我们发现，这里间隔数与棵数相等。

列式：120÷10=12

有12个间隔，所以一共要栽12棵树。

整理这个三个解决问题的过程，都经历了这么几步：一，把大数据转化为小数据；二，发现规律，并验证规律；三，运用规律，并总结形成数学思考的方法。将这三种植树问题归结到一起，我们会发现，虽然三个植树问题总结的规律不同，但都运用了化繁为简的数学思考方法。

例4：一张桌子坐6人，两张桌子并起来坐10人，三张桌子并起来坐14人……照这样，10张桌子并成一排可以坐多少人？

分析：一开始想10张桌子坐多少人，不知道如何下手。我们先来看看小一些的数据信息，两张桌子和一张桌子相比，桌子数增加了1，人数增加了4，三张桌子和两张桌子相比，桌子数增加1，人数也是增加4，因此，我们发现，只要桌子数增加1，人数就会增加4。10张桌子比6张桌子增加了9张桌子，所以人数就增加4×9=36（人）。36+6=42，所以，10张桌子可以坐42人。

这种解题过程，正是化繁为简在练习中的运用，而化繁为简又正是四道例题的共性所在。因此，将这种同类但不同型的例题做对比时，不光要体现区别，更要注重多题归一，寻找解题规律。

（作者单位：武汉经济技术开发区实验小学）