多个多弹头在轨武器平台的目标分配优化
2018-04-26刘庆国刘新学郭会军
刘庆国, 刘新学, 夏 维, 郭会军
(1. 火箭军工程大学初级指挥学院, 陕西 西安 710025; 2. 中国人民解放军31102部队, 江苏 南京 210018)
0 引 言
随着军事航天力量在战争中的作用日趋显著,争夺制天权已经成为各军事大国在作战中的首要任务之一[1]。众所周知,卫星是军事航天力量最重要的组成部分,天基武器在反卫作战中有着不可替代的优越性:全球部署、机动性强、反应时间短等[2-3]。多弹头在轨武器平台是一种携带多个子弹的天基动能反卫星武器,单个该类型武器平台具备打击多个敌方卫星的能力,所以能够有效地减少发射成本,威慑能力更强。在此背景下,本文研究了多个多弹头在轨武器平台的目标分配优化问题。
现有相关文献包括飞行器在轨服务任务分配[4]、卫星系统的多目标分配[5]等。现有文献在指标计算时大多考虑的是“单对单”问题,在此基础上进行的目标分配优化;部分文献并未充分考虑能量的重要影响,而能量计算是造成计算量较大的关键所在。本文结合多弹头在轨武器平台“单对多”的武器特点,建立了基于遗传算法(genetic algorithm, GA)的单个多弹头在轨武器平台拦截轨道优化模型,为后续计算目标分配优化的评价指标打下基础;在指标计算时将能量最优作为评价指标之一;由于计算目标分配优化时计算量较大,本文在离散粒子群算法(discrete particle swarm optimization, DPSO)[6-9]的基础上引入禁忌搜索(taboo search, TS)[10]进行局部操作以提高算法性能,在此基础上建立了基于DPSO-TS算法的目标分配优化模型;仿真结果表明该算法能够快速有效地解决多个多弹头在轨武器平台的目标分配优化问题。
1 单个多弹头在轨武器平台的拦截轨道优化模型
多弹头在轨武器平台实施打击地过程为:在轨控/姿控发动机的作用下,携带子弹机动变轨,当调整到合适轨道后释放第一个子弹(即子弹释放后按照当前速度位置可以实现对目标卫星的打击),而后武器平台再次机动变轨,准备释放下一个子弹,以此类推。该小节为后续计算目标分配优化的评价指标打下基础。
在忽略各种摄动力的前提下,本文基于单脉冲拦截假设,以总速度增量‖Δvall‖最小值作为单个多弹头在轨武器平台的拦截轨道优化模型的目标函数,表示为
(1)
式中,ti为武器平台机动变轨时刻;n为拦截目标个数。其约束条件为
(2)
式中,Tmax为多弹头在轨武器平台拦截目标卫星的时间上限;n为子段数目;Δvi为第i段轨道的速度增量;Δvmax为最大速度增量。
轨道消耗的燃料质量表示为
(3)
式中,Δmi为第i段轨道消耗的燃料质量;g0为重力加速度;mi为第i段轨道的起始时刻质量。
利用GA对武器平台机动时刻进行全局优化搜索,进而通过求解Lambert问题(见图1),得到单脉冲拦截的速度增量,单个多弹头在轨武器平台在原轨道运行时,点P1处的位置矢量和速度矢量分别为r1和v1,假设单个多弹头在轨武器平台在点P1处进行变轨,飞行Δt时间到达点P2,其在P1、P2处的位置矢量分别为r1、r2,速度矢量分别为v1、v2,则多单个弹头在轨武器平台在点P1处速度增量Δv的确定即为Lambert问题。Lambert问题的具体求解过程参考文献[11]。
GA[12-13]的实现步骤如下:
步骤1对武器平台机动时刻t1,t2,…,tn进行编码,随机产生50个染色体作为初始种群,设置交叉概率为Pc,变异概率Pm,最大迭代次数N。
步骤2适应度函数为fitness=1/‖Δvall‖,计算种群个体的适应度值及群体的适应度值总和。
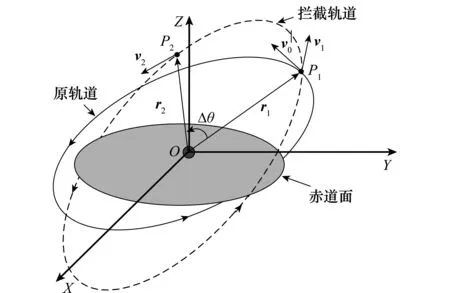
图1 Lambert问题Fig.1 Lambert problem
步骤3利用轮盘赌(roulette wheel selection, RWS)方法进行选择,轮盘中的区域大小与适应度函数值成正比(见图2),每转动一轮,指针指向的作为繁殖后代的个体(R1,R2,…,Rk表示染色体1,2,…,k);本文采用单点交叉作为交叉方式:在选择两个交叉个体后,随机选取交叉点,然后将两个交叉体位于交叉点右侧的基因进行交换;假设变异概率为Pm变异的具体操作为:产生(0,1)上的随机数α,若α≤Pm,则改变随机染色体上随机位置的基因值。

图2 轮盘赌Fig.2 Roulette wheel selection
步骤4重复执行步骤2、步骤3,直到算法收敛或者达到最大迭代次数。
通过上述方法即可求解给定顺序的‖Δvall‖,进而可以得到完成拦截所需的最少燃料质量。
2 基于DPSO-TS算法的目标分配优化模型
由于多弹头在轨武器平台的目标分配优化问题中计算评价指标时(尤指评价指标(2))计算量较大,所以快速计算成为影响解决该问题的关键。本文的DPSO-TS算法是DPSO与TS相结合的一种混合算法。惯性权重是DPSO算法的一项重要参数,其值越大则全局搜索能力越强,越小则局部搜索能力越强[14-15],本文在具有较强全局搜索能力DPSO算法的基础上加入局部搜索能力较强的TS算法,进而提高算法性能,使算法能够快速收敛。
2.1 目标分配的数学描述
假设有个多弹头在轨武器平台W=(W1,W2,…,WN),M个目标卫星T=(T1,T2,…,TM),每个多弹头在轨武器平台携带K个子弹,定义目标分配矩阵XN×M[16-18]中各元素为
(4)
可以得到多弹头在轨武器平台目标分配问题[19-20]的数学描述为
maxf(X)=(f1,f2,…,fn)T
(5)
式中,(f1,f2,…,fn)为评价指标;K为多弹头在轨武器平台携带的子弹数目;mxi为第i个多弹头在轨武器平台消耗的燃料;mmax为单个多弹头在轨武器平台携带总燃料。约束条件的意义在于:单个武器平台最多打击K个目标卫星;单个目标卫星最多被一个子弹打击;单个多弹头在轨武器平台消耗燃料不得多于携带总燃料。
2.2 优化指标
对于数学描述中的优化指标f(X)=(f1,f2,…,fn)T主要包括两个方面:一是打击目标卫星的数目,二是完成打击后所有多弹头在轨武器平台中单个武器平台剩余燃料的最小值。
(1) 打击目标数目
打击的目标数目越多,对敌方的破坏越大,则以打击目标数目作为评价指标,即
(6)
(2) 单个多弹头在轨武器平台剩余燃料的最小值
平台剩余燃料为用来机动变轨的剩余燃料。该评价指标是在评价指标(1)的基础上计算的,即评价指标(1)达到最大后再考虑该评价指标。单个多弹头在轨武器平台剩余的燃料越多,其在轨时间越长,对目标卫星的在轨威慑时间越长。为了强调对所有目标卫星的总体控制,则以单个多弹头在轨武器平台剩余的燃料最小值作为评价指标,即
f2(X)=min{mx1,mx2,…,mxn}
(7)
在计算评价指标(2)时,需要通过第1节单个多弹头在轨武器平台的拦截轨道优化模型求解剩余燃料质量。
通过上述分析,得到优化指标f(X)为
(8)
式中,k1、k2为权重系数,为了体现评价指标(2)是在评价指标(1)的基础上计算的,本文用式(9)来约束k1、k2的取值。
(9)
式(9)的含义在于增加或者减少一个打击目标(指标1)对评价指标的影响大于全部用来机动变轨燃料剩余(指标2)对于评价指标的影响,如果优化结果f1对应的打击目标数目小于优化结果f2,即使f1燃料全部剩余,其优化指标值也将会小于f2。
2.3 DPSO算法的元素构建
(1) 粒子编码
采用实数编码方式,粒子长度为KN,K为多弹头在轨武器平台携带的子弹数目,N为多弹头在轨武器平台数目,其编码方式如图3所示。
(2) 粒子适应度计算
采用式(8)作为粒子适应度函数f(X)。
(3) 位置和速度更新公式
粒子的位置是由粒子的速度、个体极值和全局极值作用的结果,其位置和速度的更新公式为
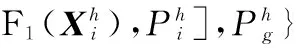
(10)
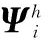

(13)
式(11)表示粒子对自身飞行速度的思考,rand()表示区间(0,1)上的随机数,当rand()<ω时,即在[1,N]之间产生2个随机数a和b,粒子产生a,b两个位置并进行交换;式(12)表示粒子根据Pi调整位置,c1为两者的交叉概率;式(13)表示粒子根据Pg调整位置,c2为两者的交叉概率。式(12)和式(13)的位置产生方式和式(11)一致。
2.4 DPSO-TS算法的步骤及流程图
TS算法的计算是在每计算一步DPSO算法后进行的,TS算法的基本元素包含:初始解、适配值函数、邻域、移动、候选集、禁忌表及其长度、特赦准则、多样性搜索策略和终止条件等。各元素的具体含义参考文献[10]。基于TS算法的局部操作流程如下:
步骤1设置参数,算法初始化,包括禁忌长度LT,候选集大小MT以及最大迭代次数TMT。
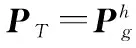
步骤3根据集中性与多样性搜索策略,生成当前解的邻域,并且从邻域中选取NT个粒子作为候选集Openlist(Y)。
步骤4根据计算的适度值fitT(Yi),判断是否满足特赦准则,若满足,则用被解禁的候选解代替当前的Yi,并将Yi置入禁忌表;若不满足,保持Yi不变。
步骤5从Openlist(Y)中选出未被禁忌表Tabulist(Z)所禁忌的当前最优解,更新Tabulist(Z)。
步骤6判断是否满足禁忌搜索的终止条件,若满足,则输出PTbest;若不满足,执行步骤3。
依据上述内容,基于DPSO-TS算法的目标分配优化计算流程图如图4所示,具体流程如下:
步骤1设置参数,设定粒子群的规模大小P,多弹头在轨武器平台的数目N,单个多弹头在轨武器平台的子弹数目K,最大迭代次数TM,以及ω、c1和c2。
步骤2初始化种群并计算各粒子的适应度函数值f(X),记录初始个体极值Pi和全局极值Pg。
步骤3利用式(10)更新粒子的位置,计算适应度函数值f(X)并更新Pi和Pg。
步骤4TS算法初始化,包括候选集大小MT,最大迭代次数TMT以及禁忌长度LT。
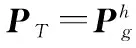
步骤6根据多样性与集中性搜索策略,生成解的邻域,并且从邻域中选取NT个粒子作为候选集Openlist(Y)。
步骤7判断fitT(Yi)是否满足特赦准则,若满足,则用满足的解代替当前的Yi,并将Yi置入禁忌表;若不满足,保持Yi不变。
步骤8从Openlist(Y)中选出未被禁忌的当前最优解,并更新Tabulist(Z)。
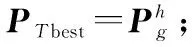
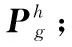
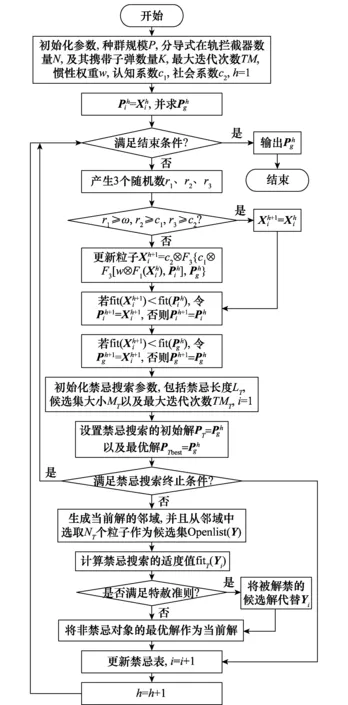
图4 DPSO-TS算法的计算流程图Fig.4 Calculating flow of DPSO-TS
3 仿真计算及结果分析
3.1 仿真条件
本文给定3个多弹头在轨武器平台(A1、A2和A3)以及22颗目标卫星(T1~T22)的轨道参数如表1所示。本文假设单个多弹头在轨武器平台的质量为1 000 kg,携带燃料250 kg,Tmax为8小时,同时每个多弹头在轨拦截器至少剩余50 kg燃料用来轨道保持;发动机比冲为300 s,发动机推力的最大值为480 N;粒子群的规模P=10,最大迭代次数TM=20,为了提高粒子群算法的全局搜索能力,设定惯性权重,认知系数,社会系数;在进行禁忌搜索时,从邻域中随机选取5个作为候选解,即NT=5;依据式(9),给定评价指标中的权系数k1,k2分别为0.996和0.004。
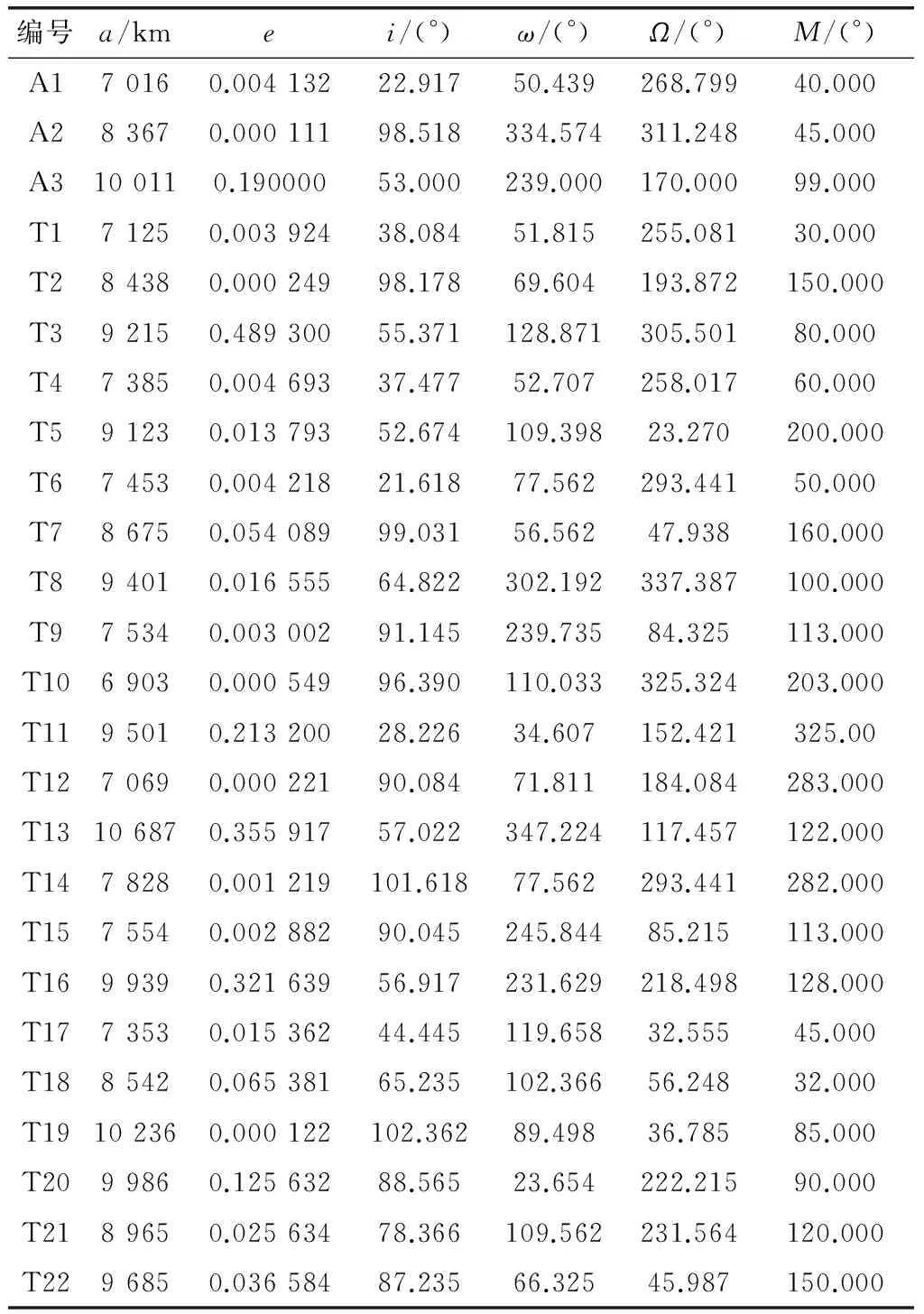
表1 武器平台和目标卫星的轨道参数
3.2 仿真结果及分析
DPSO算法和DPSO-TS算法的算法性能如表2所示,两者的收敛曲线以及两者最优解对比随迭代次数的变化曲线分别如图5~图7所示,随迭代时间的变化曲线分别如图8~图10所示。表2给出了图5~图10中的关键参数,通过仿真结果可以看出,DPSO和DPSO-TS算法两者运算得到的结果一致:两者的优化指标值均为9.372,多弹头在轨武器平台A1对应的目标卫星为T1、T12和T14,A2对应的目标卫星为T6、T9和T16,A3对应的目标卫星为T8、T19和T20;DPSO-TS算法迭代4次后终止计算并得到最优解,迭代时间为392.852 s,DPSO算法在迭代8次后终止计算并得到最优解,迭代时间为721.329 s。

表2 DPSO和DPSO-TS的算法性能比较
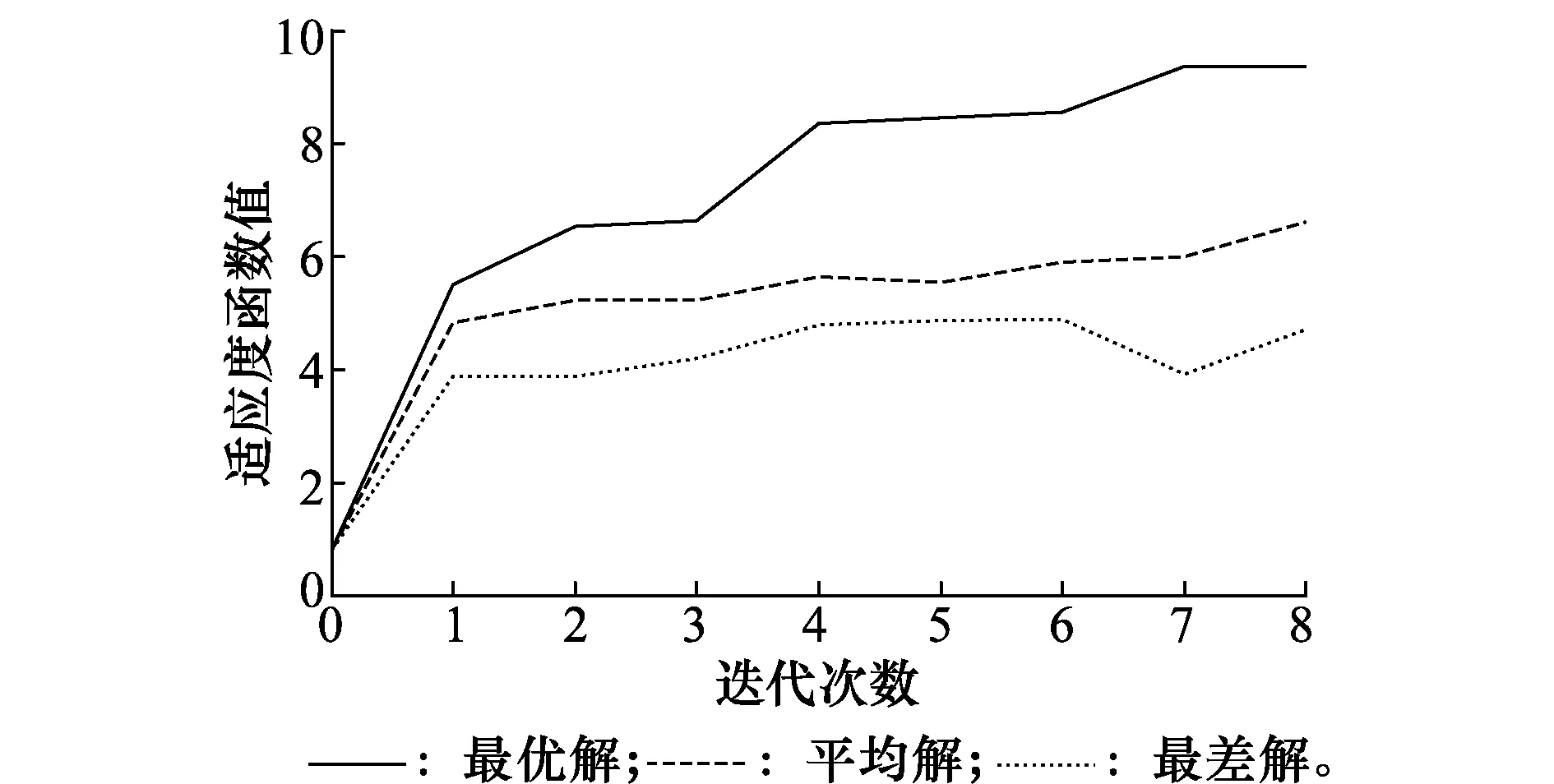
图5 DPSO算法收敛曲线Fig.5 Convergence curve of DPSO algorithm

图6 DPSO-TS算法收敛曲线Fig.6 Convergence curve of DPSO-TS algorithm
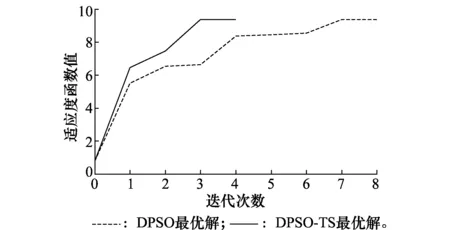
图7 DPSO和DPSO-TS的算法收敛曲线对比图Fig.7 Convergence curve comparison between DPSO and DPSO-TS
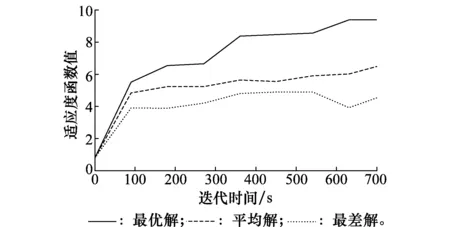
图8 DPSO算法收敛曲线Fig.8 Convergence curve of DPSO algorithm
仿真结果表明DPSO-TS算法在保证优化结果与DPSO算法一致的前提下,其完成计算的时间只是DPSO算法所用时间的54.5%,收敛速度更快,因此该方法能够快速有效地解决多个多弹头在轨武器平台的目标分配优化问题。
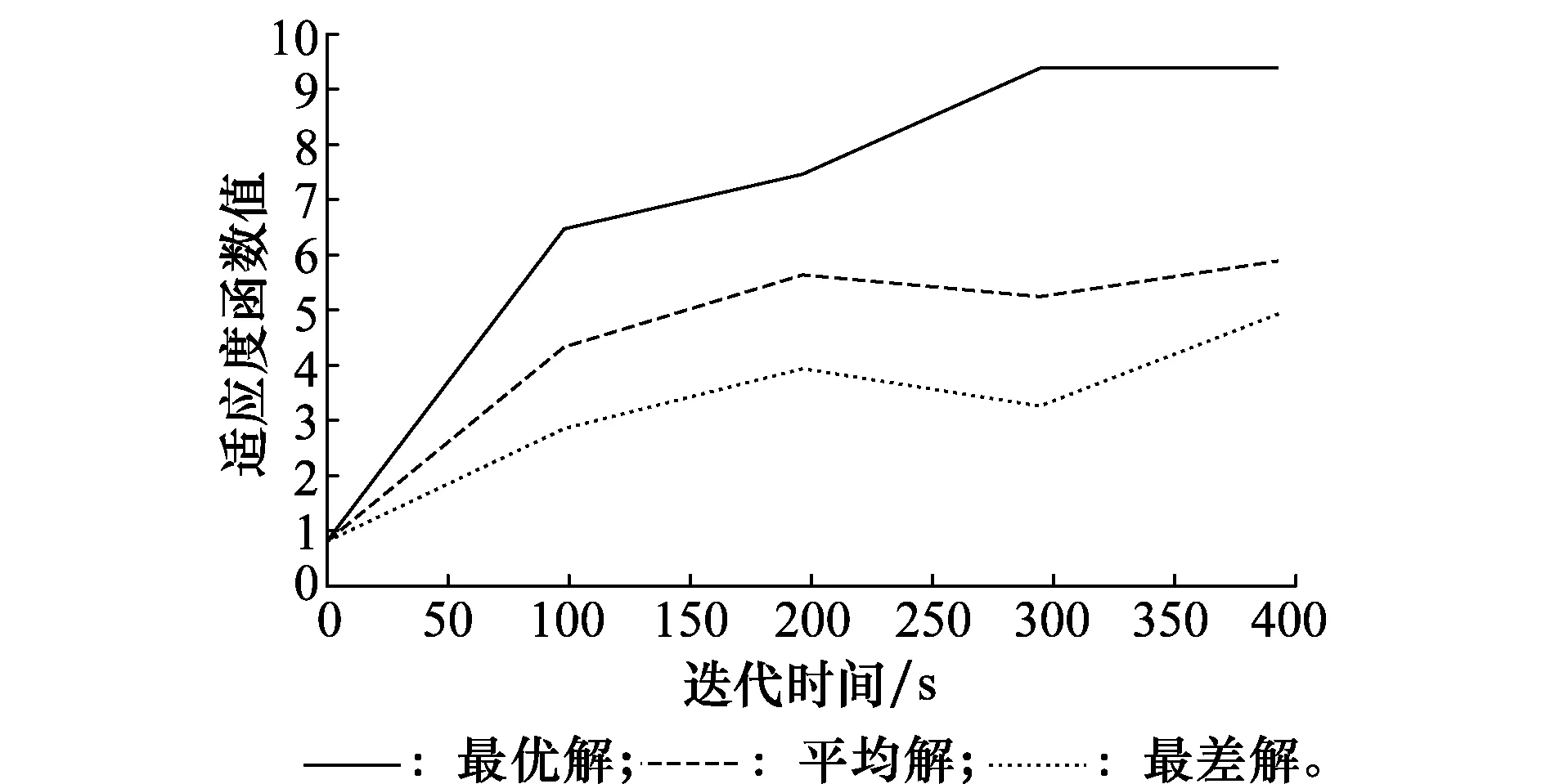
图9 DPSO-TS算法收敛曲线Fig.9 Convergence c urve of DPSO-TS algorithm

图10 DPSO和DPSO-TS的算法收敛曲线对比图Fig.10 Convergence curve comparison between DPSO and DPSO-TS
4 结束语
考虑到多弹头在轨武器平台目标分配优化时指标计算复杂的问题,本文将TS算法与DPSO算法相结合,以减少计算量;根据武器特点对粒子进行编码;为了实现多个多弹头在轨武器平台能够长期对目标卫星的控制,将能量最优作为评价之一。仿真结果表明本文采用的方法能够快速有效地解决多弹头在轨武器平台目标分配优化问题。
在计算评价指标时,实现单个多弹头在轨武器平台有限推力作用下的拦截轨道优化将会是今后研究的重点之一;轨道保持是在轨武器平台的一项关键能力,如何准确地给出轨道保持时间和所需燃料的关系也是今后研究的重点。本文着眼于解决问题实际,进一步完善了空间武器的相关理论研究,具有一定的理论研究和现实意义。
参考文献:
[1] FERGUSSON J, WONG W W S. Military space power: a guide to the issues[M].Santa Bara: Praeger, 2010:1-3.
[2] 周文雅,刘恒,李顺利,等.基于空间交会的天基反卫作战方案[J].上海航天,2009,12(3): 12-17.
ZHOU W Y, LIU H, LI S L, et al. Anti-satellite operation scheme based on space rendezvous [J]. Aerospace Shanghai, 2009,12(3):12-17.
[3] SHINAR J, OSHMAN Y, TURETSKY V. Integrated estimation guidance design for hit-to-kill accuracy [C]// Proc.of the American Control Conference, 2003: 402-407.
[4] 张琪新, 孙富春, 叶文, 等. 基于离散粒子群算法的航天器在轨服务任务分配问题研究[J]. 中国空间科学技术, 2012, 39(2): 68-76.
ZHANG Q X, SUN F C, YE W, et al. On-orbit servicing task allocation for space-crafts using discrete particle swarm optimization algorithm [J]. Chinese Space Science and Technology, 2012, 39(2): 68-76.
[5] 黄勇, 李小将, 张东来, 等. 分布式卫星系统在轨操作的多目标分配[J]. 宇航学报, 2013, 34(11): 1475-1482.
HUANG Y, LI X J, ZHANG D L, et al. A multi target assignment method for on-orbit operation of distributed satellites system [J]. Journal of Astronautics, 2013, 34(11): 1475-1482.
[6] ZOU C M. An improved particle swarm optimization [J]. Computer Knowledge & Technology, 2009, 380(16): 1-5.
[7] QIN Q D, CHENG S, ZHANG Q Y, et al. Particle swarm optimization with inter-swarm interactive learning strategy [J]. IEEE Trans. on Cybernetics, 2016, 46(10): 2238-2251.
[8] TAN G Z, BAO K, RICHARD M R. A composite particle swarm algorithm for global optimization of multimodal functions [J]. Journal of Central South University: Science and Technology, 2014, 21(6): 1871-1880.
[9] TRELEA I C. The particle swarm optimization algorithm: convergence analysis and parameter selection [J]. Information Processing Letters, 2003, 85(6): 317-325.
[10] 刘光远, 贺一, 温万惠. 禁忌搜索算法及应用[M]. 北京: 科学出版社, 2014: 35-54.
ZHAO G Y,HE Y,WEN W H. Taboo search and its application[M].Beijing: China Science Press, 2014: 35-54.
[11] 赵瑞安. 空间武器设计[M]. 北京: 中国宇航出版社, 2008: 155-181.
ZHAO R A. Space weapon design [M]. Beijing: China Astronautics Publishing House, 2008: 155-181.
[12] CHENG Y H, JIANG B, SUN J, et al. Low-thrust orbit transfer by combing genetic algorithm with refinedQ-law method[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2010, 27(4): 313-320.
[13] ZHANG X, CHENG Y H, JIANG B. Time-optimal coplanar orbit transfer using genetic-simplex algorithm [C]∥Proc.of the 3rd International Symposium on Systems and Control in Aeronautics& Astronautics, 2010: 12-16.
[14] WANG S Z, MENG B. Chaotic particle swarm optimization algorithm for support vector machine [C]// Proc.of the IEEE International Conference on Bio-Inspired Computing: Theories and Applications, 2010: 1654-1657.
[15] TATSUMI K, IBUKI T, TANINO T. A chaotic particle swarm optimization exploiting a virtual quartic objective function based on the personal and global best solutions [J]. Applied Mathematics and Computation,2013,219(17):8991-9011.
[16] LEE Z J, SU S F, LEE C Y. Efficiently solving general weapon-target assignment problem by genetic algorithm with greedy eugenics [J]. IEEE Trans. on Systems, Man, and Cybernetics, Part B: Cybernetics, 2003, 33(1): 113-121.
[17] ZBIGNIEW R B, ANTONY T, KETULA P. Effect-based weapon-target assignment with minimized collateral damage [J]. International Journal of Operational Research, 2016, 27(4): 624-641.
[18] MEKAWEY H I, ABDEL W M S, HASHEM M. Novel goal based weapon-target assignment doctrine [J]. Journal of Aerospace Computing, 2009, 27(6): 622-629.
[19] BHABANI S P M, EUIWHAN K, GUCK C B, et al. Weapon target assignment problem: multi-objective formulation, optimization, using MOPSO and TOPSIS [J]. International Journal of Intelligent Defense Support Systems, 2015, 5(3): 226-252.
[20] ONUR O. A mathematical approach to neuron marketing: a weapon-target assignment model [J]. International Journal of Academic Research in Business and Social Sciences,2016,6(1): 164-173.
