基于矩阵分解的惯导安装误差矩阵解耦方法

吴华丽, 肖支才, 周大旺, 王玲玲

(海军航空工程学院控制工程系, 山东 烟台 264001)

0 引 言

惯性仪表误差是捷联惯性导航系统(strapdown inertial navigation system，SINS)的重要误差源,对导航精度有重要影响。因此,对惯性仪表误差参数的精度具有很高的要求[1-4]。然而,惯导系统由于自身及外界等多种原因影响,使用一段时间后需要对惯性仪表的误差参数重新标定[1,3]。惯导的标定方法常分为分立标定和系统级标定,而对于惯导的定期标定一般使用系统级标定方法[1,5-6]。系统级标定指的是利用导航输出误差对惯性仪表参数进行标定的方法,这是一种能有效减小标定对转台依赖的方法,适合外场标定使用[3,7]。然而与分立标定方法相比,其对安装误差矩阵不能有效辨识,根本原因是惯性仪表的12个安装误差参数存在3组耦合关系[8-13]。这种耦合关系存在,不但影响传统惯性仪表的标定工作,还对不断发展的微电子机械系统惯性测量单元(micro electronical mechnical system inertial measurement unit,MEMS IMU)的标定产生重大影响[14-18]。因此,如何解决这种耦合关系成为一个重要待解决问题。

针对这个问题,传统方法是直接将陀螺仪表组安装误差矩阵的上三角定义为0(下文称这种解耦方法为传统方法)[8,11-12],而文献[10]则通过引入加速度计的脉冲输出加入限制条件。总结这些传统解耦方法发现其没有深入分析耦合原因。比如:文献[10]虽从可辨识性出发指出了耦合现象,但是并没有分析耦合引起的原因,其利用加速度计脉冲输出引入的限制条件虽然可以求解待标参数,但是该方法只适合转台标定;文献[8]虽然通过导航方程指出这种参数耦合原因是导航系表示的观测量对载体坐标系b系缺乏约束引起,但是没有进一步分析其使用传统方法的依据是什么,也无法给出该方法是否为最佳方法。

针对上述问题,本文利用矩阵分解的方法深入分析耦合生成原因,提出使陀螺斜对称误差矩阵为零的最佳解耦方法。首先推导了分解后的误差矩阵对姿态和速度方程的影响;接着深入分析引起安装误差矩阵耦合的原因,从更深层次揭露了这种耦合关系,并在此基础上提出最佳解耦方法;然后将本文方法与传统方法进行对比分析;最后利用两种方法进行标定仿真,并对标定结果进行原位导航,仿真结果验证本文所提方法是有效的。

1 问题描述

惯性仪表误差模型(待标参数模型)[10]为

(1)

(2)

假设待标参数误差为常值误差,随机噪声为零均值不相关白噪声,则

(3)

为了论述方便,记δKω和δLa构成的各个元素分别为

(5)

式中,δKii和δLii(i=X,Y,Z)表示惯性传感器的刻度系数;δKij和δLij(i≠ji,j=X,Y,Z)表示惯性传感器的安装误差系数。

(6)

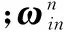
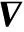
2 基于矩阵分解的解耦方法

2.1 安装误差矩阵分解

下面首先给出矩阵分解原理。

引理1矩阵分解原理[20],任何矩阵A可分解成对称矩阵和斜对称矩阵之和,即

(7)

式中,矩阵F为斜对称矩阵(FT=-F);G为对称矩阵(GT=G)。

根据引理1可以将刻度系数/安装误差矩阵分解成两部分:斜对称误差矩阵和对称误差矩阵,用数学表达式表示为

(8)

式中,δKScal/sym,δLScal/sym表示δKω,δLa中的对称误差矩阵;δKSksym,δLSksym表示δKω,δLa中的斜对称误差矩阵。

由于δKSksym,δLSksym具有斜对称性,还可以写成向量叉积形式，即

(9)

由于对称误差矩阵δKScal/sym,δLScal/sym包含了刻度系数误差和安装误差的对称性误差,将其分开表示,则可分解为

(10)

式中,δKScal表示刻度系数误差,是一个对角阵;δKSym表示安装误差的对称性误差。

因此,式(8)可以表示为

(11)

根据矩阵分解原理,矩阵分解后的误差矩阵物理含义为:斜对称误差矩阵δKSksym和δLSksym表示安装误差阵的不对准特性,指惯性仪表组相对参考轴的不对准;对称性误差矩阵δKSym和δLSym表示安装误差阵的非正交特性,指惯性仪表组输出轴之间是非正交的;对角矩阵δKScal和δLScal表示刻度系数误差。

根据对称误差矩阵和斜对称误差矩阵性质,可以得到

(12)

(13)

(14)

(15)

式(15)说明了可以通过刻度系数/安装误差矩阵来求解对称误差矩阵和斜对称误差矩阵,为实际应用提供方便。

为了理解斜对称误差矩阵和对称误差矩阵物理意义,以二维平面为例进行解释。

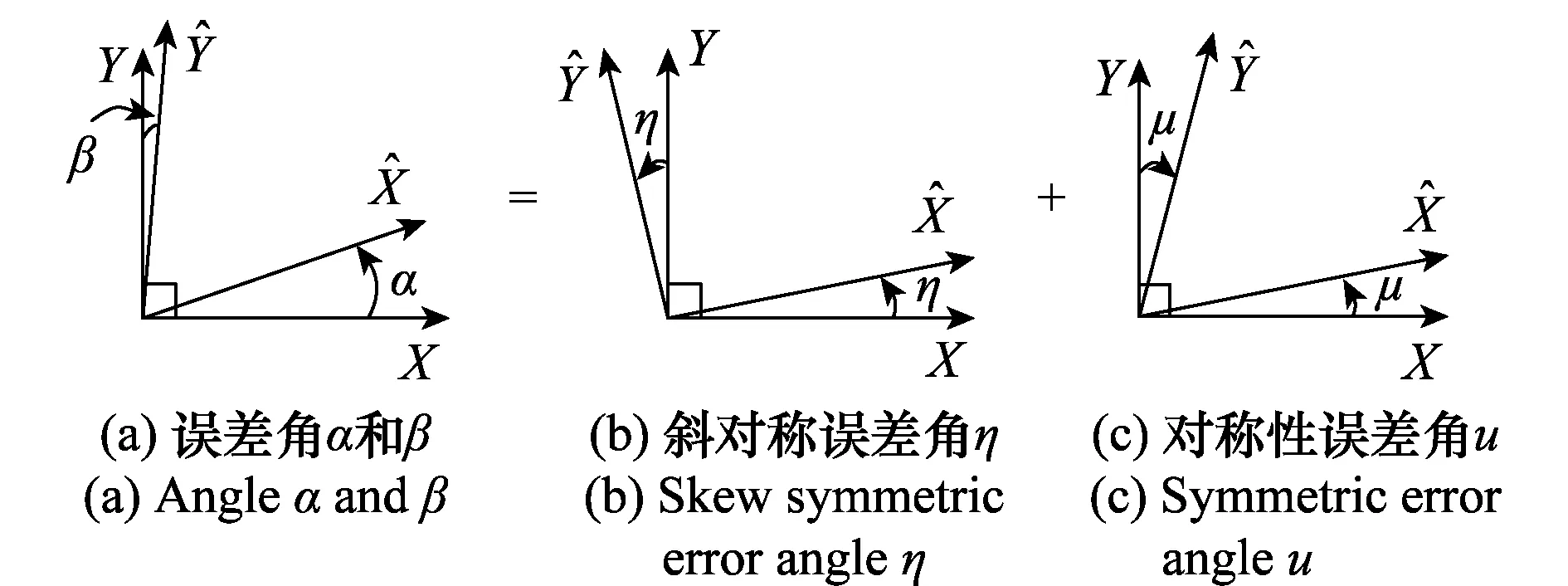
图1 安装误差矩阵的分解Fig.1 Decomposition of installation error matrix

从二维平面可以看出,安装误差矩阵分解就是将这两类误差分开,其中斜对称误差矩阵是因坐标系失准导致的,对称误差矩阵是非正交特性导致的。

对陀螺仪表组安装误差矩阵分解是对二维平面物理意义分析,该过程同样适用于加速度计的安装误差分解阵的解释。

2.2 两类误差对捷联惯导姿态和速度方程的影响

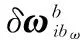
(16)

将式(10)和式(11)代入式(16),可得

(17)

δfb=δLScalfb+δlSksym×fb+δLSymfb

(18)

2.2.1 两类误差对姿态误差方程的影响

(19)

(20)

对式(20)两边微分可以得到

(21)

将式(17)的误差方程代入式(21)得

(22)

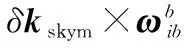
(23)

从式(23)可以看出,斜对称误差不影响陀螺仪误差的增长,即不对姿态误差增长有影响。

接着分析斜对称误差对姿态方向影响，这种影响可以通过将该部分影响代入式(19)进行分析，得

(24)

对式(24)进行积分可得

(25)

式(25)说明斜对称误差对姿态误差影响等价于加入一个从t=0开始的从b系到i系的姿态误差。

2.2.2 两类误差对速度误差方程影响

从捷联惯导解算可以发现,安装误差是通过比力fn对系统速度产生影响,而比力fn将通过被积分得到系统速度。因此若分析了安装误差对fn的影响就可以知道安装误差对系统速度的影响过程。因此仅对比力进行分析。

对惯导速度微分方程中的比力变换项进行变形得

(26)

为了分析斜对称误差的影响,对式(26)进行微分展开,得

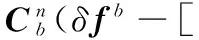
(27)

式中,Others项表示不受安装误差影响。

(28)

(29)

(30)

积分式(30)得到

(31)

将式(18)和式(31)代入式(27)可得

(32)

式(32)中相关项存在关系为

(33)

(34)

(35)

将式(33)～式(35)代入式(32)得到

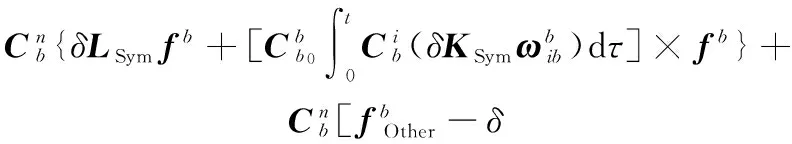
(36)

2.3 安装误差矩阵解耦方法

首先明确两个问题,第一是系统级标定的待标参数是在什么坐标系定义的,第二是误差方程在什么坐标系下解算的。由式(1)和式(2)可知,24个待标参数是针对体坐标系b系定义的,而从方程式(6)可以得知误差方程是在导航系n系中解算的。

其次分析安装误差矩阵产生耦合的原因。第2.2节内容已经推导并简要分析了分解后的斜对称和对称性误差对在n系上解算的误差方程的影响过程,可以看出参数耦合的问题。陀螺斜对称误差矩阵δKSksym对姿态误差增长无影响,对姿态误差微分项的影响是与初始姿态误差融合在一起共同影响的。因此,无法从姿态误差中分离出陀螺斜对称误差矩阵δKSksym。由式(36)可以知道加速度计组斜对称误差δLSksym对速度误差的影响是通过(δLSksym-δKSksym)项完成的,即δLSksym与δKSksym是耦合的。可见,通过捷联惯导的误差方程,无论采用什么机动方式,都无法同时分离出δKSksym和δLSksym待标参数,这里的6个参数必然存在3组耦合关系。这就是耦合产生的根源。

接着分析解耦的途径。通过分析,如果δKSksym或者δLSksym项为0,那么待标参数的3组耦合关系可以消除,从而完成解耦。但是,由于δKSksym影响不仅涉及姿态误差方程,还涉及速度误差方程,而δLSksym仅出现在速度误差方程中,因此,从二阶舍项误差最小角度分析,理论上最佳的解耦方式是使δKSksym为0。然而,是否能做到使δKSksym为0还需要进一步分析。与δKSksym为0相关联问题是δKSksym是怎么定义的。本节一开始便首先明确了δKSksym是在b系下定义的。使δKSksym=0意味着b系与I+δKSksym所确定的坐标系重合。可见,能否根据所提方式解耦的前提条件是b坐标系是否可以自由选择。然而,体坐标系定义是先决条件,只有定义了体坐标系才可以列写飞行力学方程、安装载体上的各种设备(各种设备是以这个体系为基准进行安装)等,惯性导航设备就是以这个基准安装在载体上[1,3]。可见体坐标系的确定不是任意的。国外文献一般定义体坐标系为:x轴沿着载体纵轴指向前,y轴沿着载体横轴指向右,z轴与x,y轴构成右手直角坐标系[1]。国内教科书更多使用x轴沿着载体横轴指向右,y轴沿着载体纵轴指向前,z轴与x,y轴构成右手直角坐标系的定义方法[3-4]。

最后提出解耦方法。从安装误差产生的节点考虑问题。惯性仪表组先是集中安装在IMU上,然后再安装到载体上。存在两次安装过程,相应有两次安装误差。第1次的安装误差可以按照所提的矩阵分解法分为斜对称误差和对称误差,而第2次的安装误差只有斜对称性误差,也即只有失准误差。第1次的安装误差参数可以在高精度转台上进行标定,然而第2次的安装误差是无法在转台上进行的。幸运的是，这些误差都是一个小量,可以假设体坐标系在这微小范围内是可以重新定义的。

因此,最佳解耦方法:定义体坐标系b系与I+δKSksym所确定的坐标系重合,则式(9)和式(10)中的待标参数变为

(40)

可以看出这种解耦方法其实是一种均值分配方法,使各项的安装误差进行一项平均,这种平均可以使捷联惯导计算中的二阶舍项误差影响最小。

3 与传统方法关系

分析本文所提解耦方法与传统方法的关系。

传统方法的待标参数为

(42)

式中，上标c表示传统方法。

为了得到传统方法与本文最佳方法的关系,需要梳理其各自的定义过程。设真实的体坐标系为b0,传统方法的体坐标系定义为bc,而本文的体坐标系为bnew,根据定义有下面关系:

转动b0系,使得新坐标系的z轴与z向陀螺单位矢量重合,而y向陀螺单位矢量在体坐标系的yz平面内,从而得到bc。

转动b0系,使得陀螺仪表组的安装误差失准角为0,即陀螺仪表组只存在正交性误差,则得到bnew。

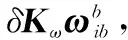
可见本文方法与传统方法的区别是体坐标系选择不同,本文的选择方法是一种均值分配方法,其使各项的安装误差进行一次平均。下面以二维平面为例对体坐标系选择进行说明。

如图2所示,xgyro,xacce,ygyro,yacce分别表示x,y向陀螺和加速度计的安装位置,x和y轴是根据载体定义的b0坐标系。xgyro,xacce,ygyro,yacce与x和y轴的误差角分别为:θx_gyro,θx_acce,θy_gyro,θy_acce。由前面分析可知,bc系是转动b0系,使x轴与xgyro重合,并且使ygyro在xy平面内,而bnew系是转动b0系,使陀螺不存在失准角,即图2中xnew位置。

图2 二维平面例子展示图Fig.2 Schematic diagram of two dimensional plane

设斜对称误差角为η,对称性误差为μ,则有

(43)

因此有

η=(θx_gyro+θy_gyro)/2

(44)

4 仿真研究

仿真首先针对系统级标定设计滤波器,然后基于该滤波器分别利用本文方法和传统方法进行标定,最后分别利用两种标定结果进行原位导航仿真。

系统级标定滤波器设计:

根据误差微分方程,设计27维Kalman滤波器。滤波器状态为

(45)

式中,Xg,Xa表示陀螺和加速度计待标参数向量,分别为

(46)

(47)

式中

(48)

滤波器方程为

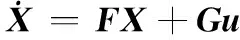
(49)

式中

(50)

其中

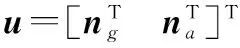
滤波器观测方程为

Z=HX+V

(51)

式中,Z=δv；V是观测噪声,观测矩阵为

H=[03×3,I3×3,03×21]

(52)

系统级标定中的转动激励采用Camberlein设计的编排方式[6],如表1所示。设转速为10°/s,转台转动中心的速度为仿真的速度观测值(速度为0),仿真中待标参数设置如表2所示。

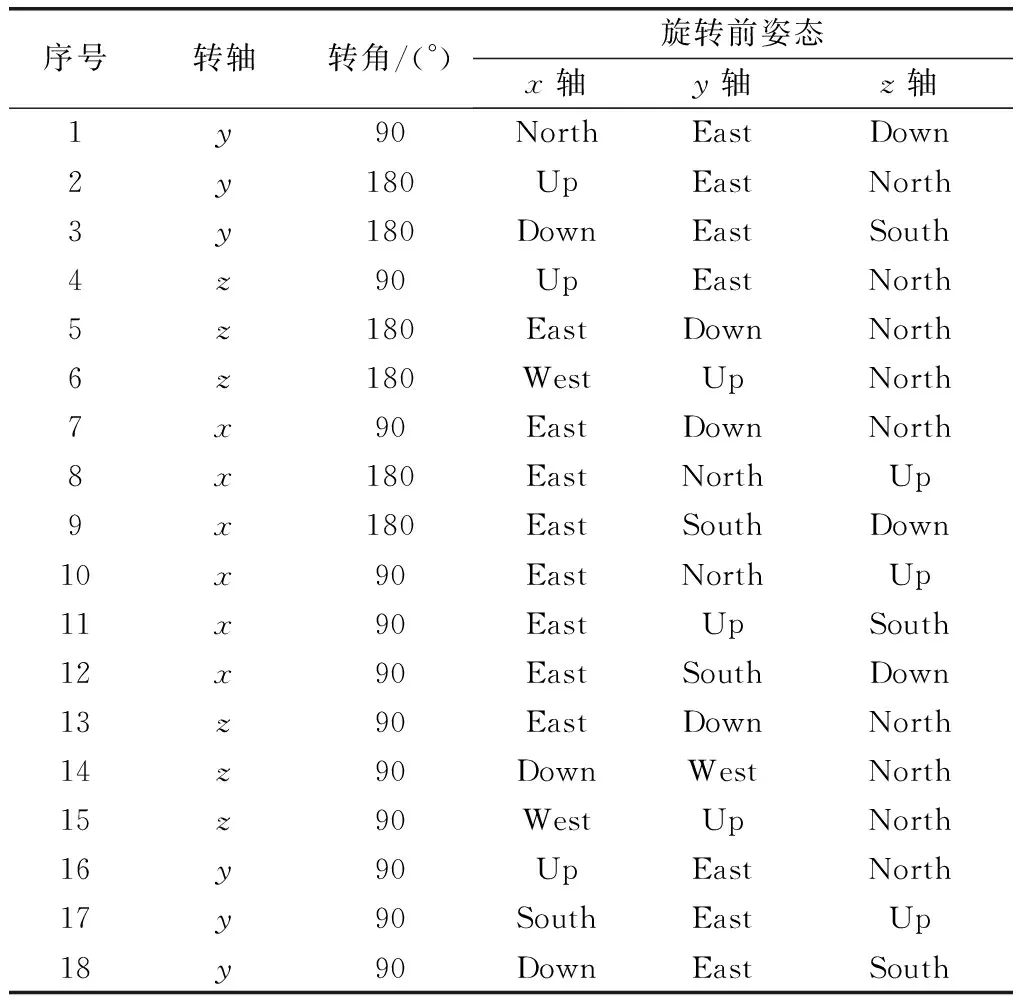
表1 Camberlein设计的编排方式

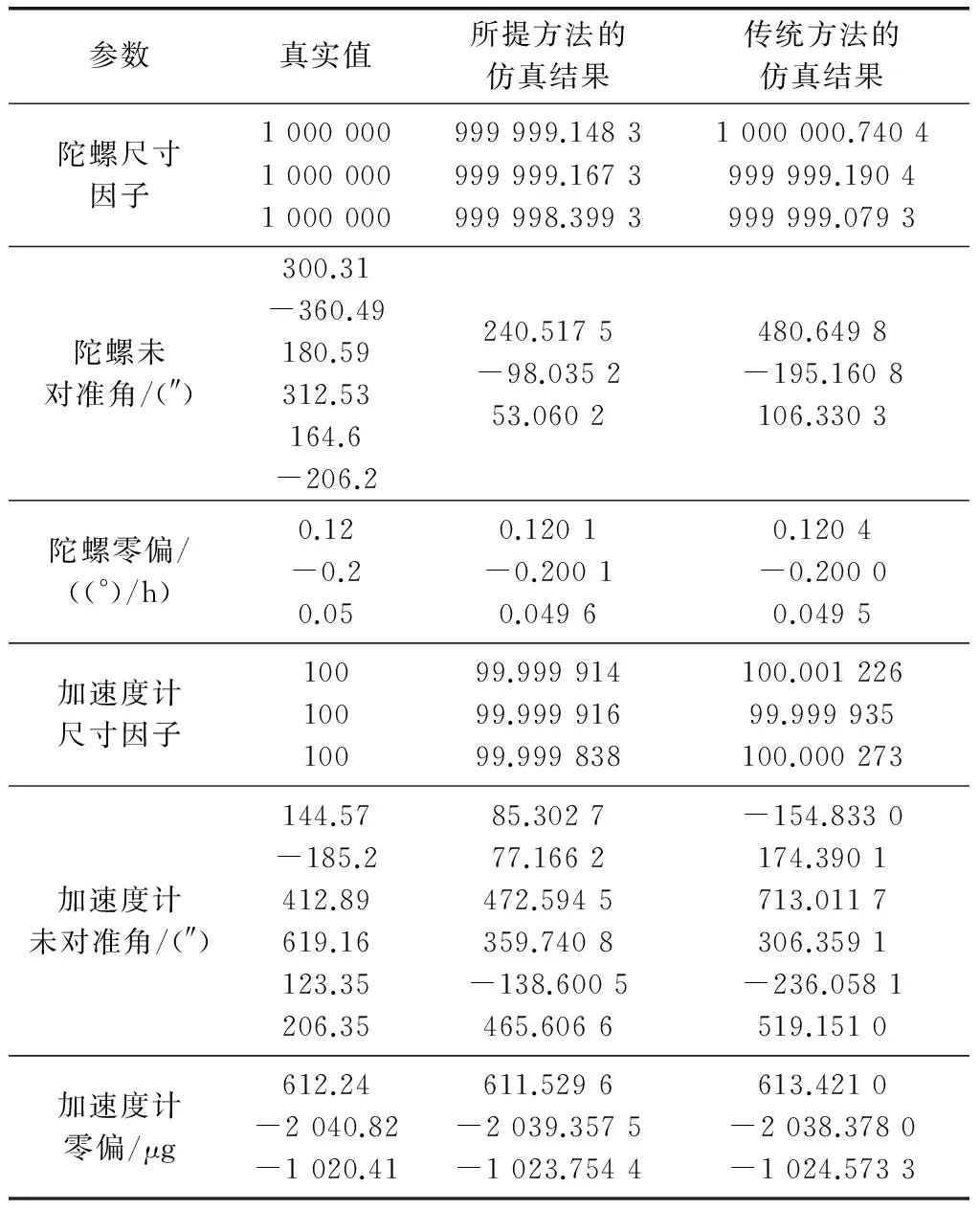
表2 待标参数仿真数值

Kalman滤波仿真结果如表2所示。其中陀螺仪安装误差角的3个参数分别为相应方法的3个待标参数。

利用标定结果进行原位导航仿真,导航结果如图3～图5所示。图3为三轴姿态误差,图4为速度误差,图5为位置误差,从仿真结果可以看出本文方法比传统方法在整体上具有小的偏差,与理论相符。

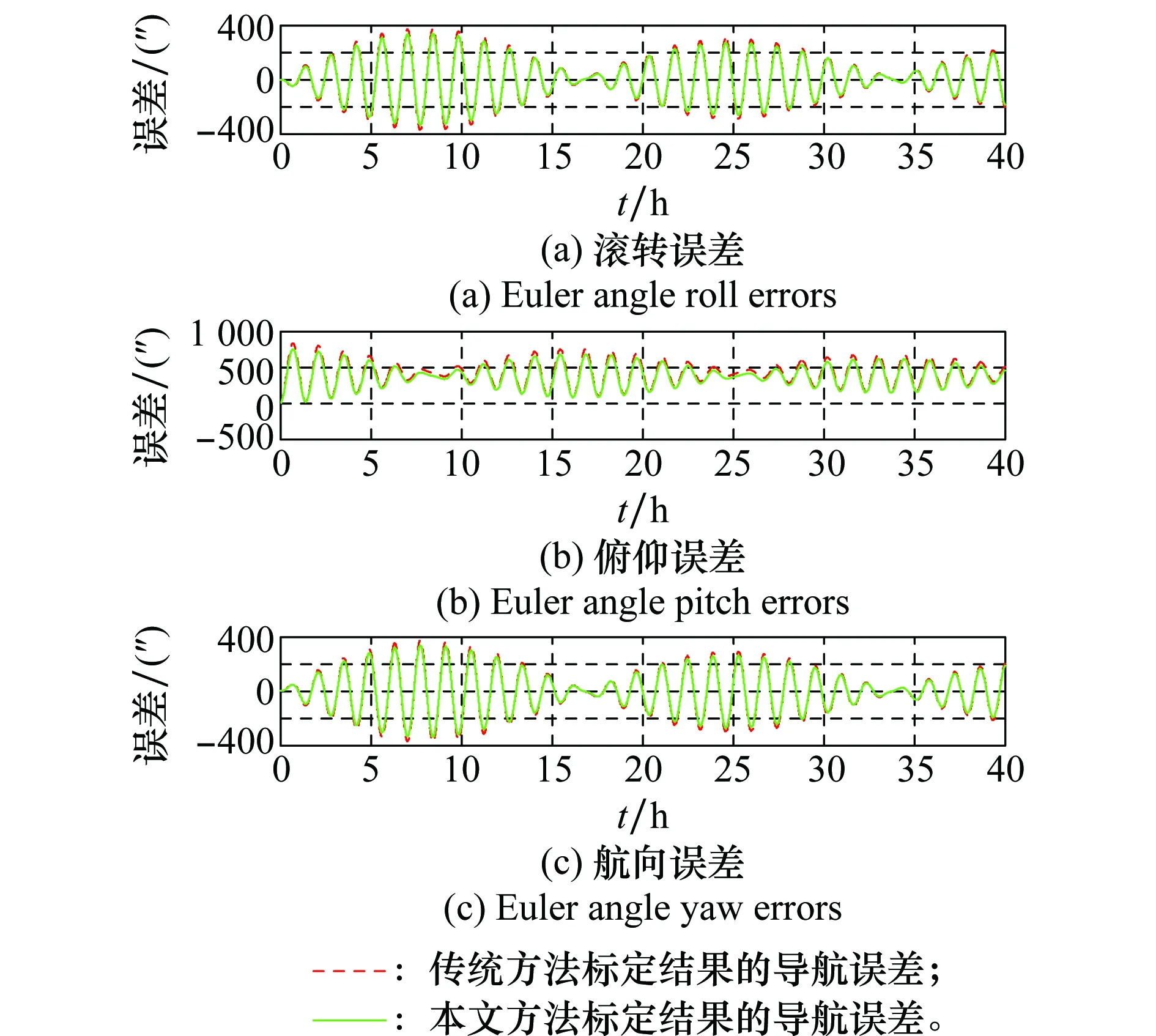
图3 姿态角误差Fig.3 Simulation results of attitude angle error

图4 速度误差Fig.4 Simulation results of velocity error

图5 位置误差Fig.5 Simulation results of position error

5 结 论

本文利用矩阵分解方法研究了惯导安装误差矩阵在系统级标定中的耦合问题,提出一种最佳解耦方法,得到如下结论:

(1) 陀螺仪表组的斜对称误差矩阵δKSksym对姿态误差增长无影响,对姿态误差的动态方程影响等价于一个初始姿态误差,而加速度计仪表组的斜对称误差δLSksym是与δKSksym通过做差对速度方程产生影响的,从而导致12个安装误差矩阵存在3组耦合关系；

(2) 最佳解耦方式是使陀螺仪表组的斜对称误差矩阵为0,即令陀螺仪表组安装误差中的失准误差为0；

参考文献：

[1] TITTERTON D H, WESTON J L. Strapdown inertial navigation technology [M]. 2nd ed. London: The Institute of Electrical Engineers, 2007.

[2] SAVAGE P G. Strapdown analytics[M]. Maple Plain, Minnesota: Strapdown Associates, Inc., 2007.

[3] 邓正隆. 惯性技术[M]. 哈尔滨:哈尔滨工业大学出版社,2006:55-57.

DENG Z L. Inertial technology[M]. Harbin: Harbin Institute of Technology Press, 2006: 55-57 .

[4] 秦永元. 惯性导航[M]. 北京:科学出版社, 2006:78-82.

QIN Y Y. Inertial navigation[M]. Beijing: Science Press, 2006:78-82.

[5] PITTMAN D N, ROBERTS C E. Determining inertial errors from navigation-in-place data[C]∥Proc.of the IEEE Position Location and Navigation Symposium, 1992:153-164.

[6] GREWAL M S, HENDERSON V D,MIYASAKO R S. Application of Kalman filtering to the calibration and alignment of inertial navigation systems[J].IEEE Trans.on Automatic Control,1991, 36(1): 4-13.

[7] CAMBERLEIN L, MAZZANTI F. Calibration technique for laser gyro strapdown inertial navigation systems[C]∥Proc.of the Symposium Gyro Technology, 1985:323-345.

[8] 张红良. 陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究[D]. 长沙: 国防科技大学,2010.

ZHANG H L. Research on error parameter estimation of land high-precision ring laser gyroscope strapdown inertial navigation system[D]. Changsha: National University of Defense Technology, 2010.

[9] 党建军,罗建军,万彦辉. 基于单轴速率转台的捷联惯测组合标定方法[J]. 航空学报,2010,31(4): 806-811.

DANG J J, LUO J J, WAN Y H. Calibration method of strap-down inertial measurement unit based on single-axis rate turntable[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(4): 806-811.

[10] 杨晓霞,黄一. 激光捷联惯导系统的一种系统级标定方法[J]. 中国惯性技术学报,2008,16(1):1-7.

YANG X X, HUANG Y. Systematic calibration method for laser gyro SINS[J]. Journal of Chinese Inertial Technology, 2008, 16(1): 1-7.

[11] LEE T G, SUNG C K. Estimation technique of fixed sensor errors for SDINS calibration[J]. International Journal of Control, Automation and Systems,2004, 2(4): 536-541.

[12] DIESEL J W. Calibration of a ring laser gyro inertial navigation system [C]∥Proc.of the 13th Biennial Guidance Test Symposium, 1987:456-462.

[13] SEONG Y C, CHAN G P. Calibration of a redundant IMU[C]∥Proc.of the AIAA Guidance, Aviation and Control Conference and Exhibit, 2004:144-162.

[14] BEKKENG J K. Calibration of a novel MEMS inertial reference unit[J]. IEEE Trans. on Instrumentation and Measurement, 2009, 58(6):1967-1974.

[15] FRISO I, PEDERSINI F, BORGHESE N A. Autocalibration of triaxial MEMS accelerometers with automatic sensor model selection[J]. IEEE Sensor Journal, 2012, 12(6):2100-2108.

[16] 刘占超,房建成. 基于双捷联算法的POS误差在线标定方法[J]. 航空学报,2012, 33(9):1679-1687.

LIU J C, FANG J C. Online calibration of POS error based on double strapdown algorithm[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(9):1679-1687.

[17] PALERMO E, ROSSI S, MARINI F. Experimental evaluation of accuracy and repeatability of a novel body-to-sensor calibration procedure for inertial sensor-based gait analysis[J]. Measurement, 2014, 52(1):145-155.

[18] KIM M S, YU S B, LEE K S. Development of a high-precision calibration method for inertial measurement unit[J]. Inertial Journal of Precision Engineering and Manufacturing, 2014, 15(3): 567-575.

[19] GOSHEN-MESKIN D, BAR-ITZHACK I Y. Unified approach to inertial navigation system error modeling[J]. Journal of Guidance Control and Dynamics, 1992, 15(3): 648-653.

[20] 许以超.线性代数与矩阵论[M].北京:高等教育出版社,2008.

XU Y C. Linear algebra and matrix theory[M]. Beijing: Higher Education Press, 2008.