基于rollout策略下的决策实体配置问题求解方法

廖梦琛, 孙 鹏,2, 张杰勇, 武君胜

(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 西北工业大学计算机学院,陕西 西安 710077;3. 西北工业大学软件与微电子学院, 陕西 西安 710077)

0 引 言

在信息化军事对抗中,如何建立战场环境下平台资源、作战任务、决策实体三者之间的关系是指挥控制(command and control, C2)组织设计中的关键问题[1-4]。当平台-任务匹配关系生成后,大量的平台资源将通过一定的规则和方法划分给有限个决策实体,建立平台与决策实体之间的配置关系RDM-P,这种关系的构建过程实质上是平台资源的聚类过程[5-6],也就是C2组织三阶段设计方法[7]中的第二阶段设计内容。

在平台聚类问题中,高效、准确的决策实体与平台之间的指挥控制关系是确保敌我对抗过程中取得优势的关键因素。文献[8]以最小化决策实体的最大工作负载为目标函数建立了数学模型,从平台、任务数量的角度衡量工作负载,并提出了基于最小工作负载的合并准则。文献[9]进一步研究了每层聚类的合并规则,定义了平台分组之间的矢量距离,提出了基于最小矢量距离的合并规则。文献[10]以作战任务的执行时间作为决策实体工作负载的测度标准,建立了以工作负载的最小均方根(root mean square,RMS)值为目标函数的数学模型,利用层次聚类法求解了该问题。文献[11]定义了指控复杂度,利用自适应量子遗传算法生成平台聚类方案。文献[12]从多个方面考虑工作负载的测度建立了多目标优化模型,通过对一系列前沿解的筛选得到符合要求的聚类方案。

层次聚类法是平台与决策实体配置关系设计的主要方法,考虑到采用传统层次聚类法在合并过程中采用了贪婪策略,即每一层的合并过程都选择当前层的最优合并方案,并未从全局的角度考虑解的最优性,得到的最终聚类方案可能不是全局最优方案。因此,本文将采用rollout策略对层次聚类法进行改进优化,以作战任务的执行时间作为决策实体工作负载的测度标准,建立平台与决策实体配置问题的数学模型,以工作负载的最小RMS值为模型目标函数,在平台合并过程中采用基于最小RMS合并准则并使用rollout策略下的层次聚类法以对该问题进行求解,通过仿真算例说明该方法能够降低工作负载的RMS值,并且能均衡每个决策实体之间的工作负载,验证了该方法的适用性,并通过和传统层次聚类法的对比分析验证了该方法的优越性。

1 问题描述及建模

1.1 变量定义

战场环境中,所有被用于作战的平台资源将被决策实体DMm控制和指挥,决策实体作为战场要素中的核心要素,负责控制平台Pj完成相应的作战任务Ti。平台与决策实体配置关系的构建的实质就是平台聚类问题。对平台聚类问题进行数学描述和建模,首先对变量作如下定义。

定义1任务与平台的分配变量ωij(i=1,2,…,I;j=1,2,…,J):如果任务Ti被分配给平台Pj执行,则ωij=1,否则ωij=0。在平台与决策实体关系设计阶段,任务与平台的分配关系作为该问题的输入信息,因此分配变量为已知量。

定义2平台与决策实体的配置变量xmj(j=1,2,…,J;m=1,2,…,D):平台需要在决策实体的指挥控制下才能执行既定作战任务,当平台Pj隶属于决策实体DMm时,xmj=1,否则xmj=0。

定义3任务与决策实体的分配变量umi(i=1,2,…,I;m=1,2,…,D):当平台与决策实体的配置关系生成后,决策实体继承了平台对任务的执行关系,即平台Pj被分配执行任务Ti,当Pj隶属于决策实体DMm时,决策实体DMm即执行任务Ti,umi=1,否则umi=0。

定义4决策实体在任务中的协作变量ymni(m,n=1,2,…,D,m≠n;i=1,2,…,I):当决策实体DMm与DMn共同执行任务Ti时,ymni=1,否则ymni=0。

1.2 约束条件分析

(1) 任何一个平台P有且只有一个决策实体DMm对其进行控制,即不存在多个决策实体控制同一个平台的情况,同时配置给任意一个平台的决策实体数量都不为0,描述为

(1)

(2) 每个决策实体至少控制一个平台,即

(2)

(3) 对于每个决策实体而言,DMm控制的每一个平台均只执行该平台分配到的任务,隶属于同一决策实体的不同平台之间的任务互不影响,即

umi≥ωij·xmj

i=1,2,…,I;j=1,2,…,J;m=1,2,…,D

(3)

已知当ymni=1时，表明决策实体DMm和DMn在任务Ti上存在协作,可以得到协作变量ymni与分配变量umi和uni之间的关系为

ymni=min(umi,uni),m≠n;i=1,2,…,I

(4)

1.3 决策实体配置问题的目标函数和模型建立

1.3.1 决策实体工作负载的定义

决策实体的工作负载反应了隶属于该决策实体的平台资源对作战任务的执行情况。在考虑决策实体的工作负载时,选择以面向作战任务的形式,将作战任务的执行时间作为工作负载的测度标准,从内部工作负载I(m)和外部工作负载E(m)两个方面对工作负载进行描述[8]。

(1) 决策实体DMm的内部工作负载I(m)

决策实体的内部负载表示决策实体控制的平台所承担的工作负载,数值上表示为所控制平台处理的全部作战任务的时间之和,即

(5)

式中,ti为任务Ti的执行时间。

(2) 决策实体DMm的外部工作负载E(m)

决策实体的外部工作负载表示决策实体所控制的平台和其他决策实体协作处理任务时承担的工作负载,数值上表示为与其他不属于该决策实体的平台协作执行的全部作战任务的时间之和,即

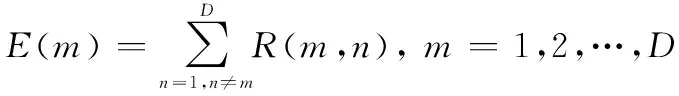
(6)

式中,R(m,n)表示决策实体DMm与DMn协作处理作战任务的时间之和

n=1,2,…,D;m≠n

(7)

结合式(6)、式(7),决策实体的外部工作负载可以表示为

(8)

(3) 总工作负载CW(m)

决策实体的总工作负载以内部工作负载I(m)与外部工作负载E(m)加权和的形式表示,即

CW(m)=WI·I(m)+WE·E(m)

(9)

式中,WI表示内部工作负载权重；WE表示外部工作负载权重。WI和WE分别表示对总工作负载的影响程度。一般地,取WI=WE=1。

1.3.2 目标函数的构造

在平台与决策实体配置问题中,已知的输入信息为平台-任务的调度关系,当平台-任务的调度方案生成后,初始的决策实体工作负载的内部负载部分将不再发生变化,因此对于该平台聚类过程实质上就是最小化外部工作负载的过程。

由于每个决策实体的能力有限,如何对平台进行合理地分组、将分组的平台配置给有限数量的决策实体,是实现决策实体对平台的指挥控制的关键。在这一问题中,一方面要求所有决策实体的平均工作负载尽可能小,另一方面要求所有决策实体的工作负载尽可能均衡。因此,目标函数从均值和方差两个方面进行描述:

(1) 工作负载的均值

(10)

式中,D表示决策实体的个数,对于该问题的目标函数而言,工作负载的均值μ越小越好。

(2) 工作负载的方差

(11)

工作负载的方差σ2体现了每个决策实体工作负载的差异,因此对于该问题工作负载之间的方差σ2越小，表示每个决策实体的工作负载越均衡。

因此,决策实体工作负载的RMS可以表示为

(12)

1.3.3 数学模型建立

由式(12)可知,工作负载的RMS值综合了工作负载的均值和方差两个方面，充分体现了每个决策实体工作负载的水平,因此,本文构建的平台与决策实体配置问题的数学模型为

(13)

2 基于rollout策略下的层次聚类法求解方法

2.1 rollout策略

平台聚类的问题即将不同的平台分配给一定数量的决策实体,由决策实体控制各个平台执行既定的作战任务。在聚类过程中,要在满足问题约束条件的同时得到符合问题模型目标函数的最优解,因此平台聚类方案体现了所设计的平台与决策实体之间配置关系的合理性。使用层次聚类法实现平台聚类的过程可以描述为:将当前的J个平台按照某一合并规则进行合并,选择合并后使目标函数值满足问题模型的需求的两个平台进行合并,逐层合并直至平台个数J与决策实体数量D相同时合并结束。

传统的层次聚类方法在逐层合并的过程中均采用了贪婪策略,最终形成决策实体与平台的指挥关系。然而,这种每层合并都基于贪婪策略的解只考虑了当前层的最优性,得到的最终聚类结果可能不是全局最优解。为了改善最终聚类结果的性能和效果,本文将采用rollout策略[13-15]对层次聚类法的合并过程进行改进。基于rollout策略改进的层次聚类法的基本思想是:每一层生成m个备选合并方案,这些方案按照目标函数值大小排序,令当前层的合并方案分别为1,2,…,m,后续的平台合并过程均采用贪婪策略生成最终聚类方案,若当前层的第p个合并方案使最终目标函数值最小,则选用p方案作为当前层的合并方案,进入下一层合并重复该过程,直至满足结束条件。合并过程如图1所示。

图1 rollout策略下的层次聚类法的合并过程Fig.1 Merge processing of hierarchical clustering algorithm based on rollout strategy

2.2 最小RMS的平台合并准则下的聚类过程

本文提出了基于rollout策略下的层次聚类法对该问题进行求解。根据式(13)中的问题目标函数,选择任意两个平台进行合并,合并后计算生成的所有决策实体的工作负载的RMS值,根据聚类后的RMS值生成m个当前层的备选合并方案,每个方案后续的合并过程均采用贪婪算法,利用rollout策略确定当前层的最佳合并项。满足该条件的平台合并规则称为基于最小RMS平台分组合并规则[10],基于rollout策略的层次聚类法在该合并规则下的聚类流程如图2所示。

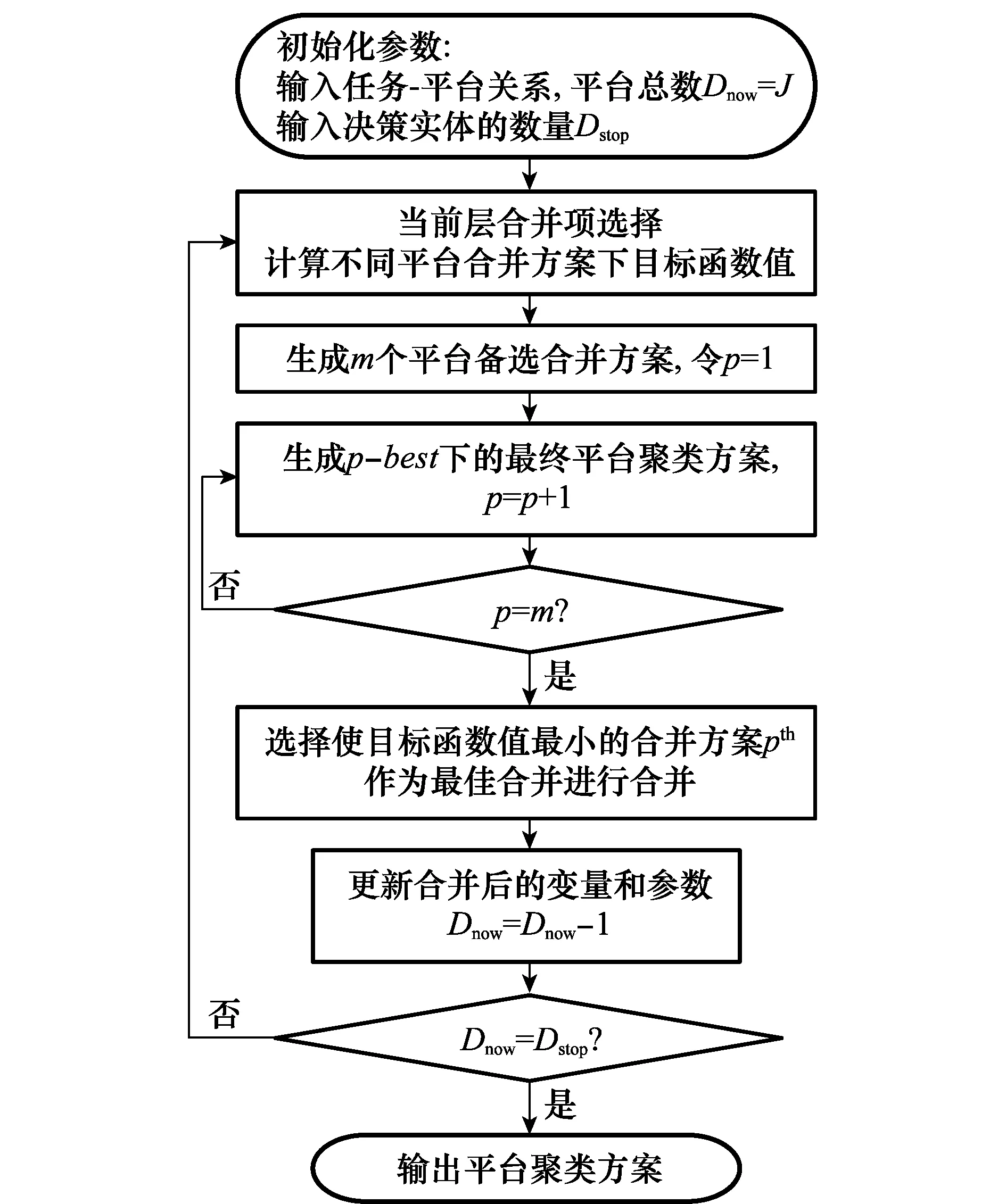
图2 rollout策略下的层次聚类法聚类流程图Fig.2 Flowchart of hierarchical clustering based on rollout strategy

步骤1选择任意的两个平台进行合并

平台聚类开始前,假设每一个平台由一个决策实体控制,此时的决策实体的数量Dnow与平台数量J相等。聚类开始时,选择任意两个决策实体DMh与DMk进行分组合并(h,k=1,2,…,Dnow, 且h≠k),合并后的形成新的决策实体DMg,此时新决策实体的DMg的总工作负载为

CW(g)=CW(h)+CW(k)-

(14)

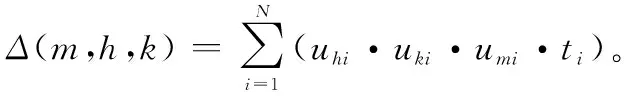
经过合并后,其他决策实体DMm的工作负载也要进行相应地更新,具体体现为消除合并后的两个决策实体对于其他决策实体而言产生重叠的外部工作负载。更新后的决策实体DMm的工作负载表示为

CW(m)=CW(m)-WE·Δ(m,h,k),m≠h,k

(15)

步骤2计算合并后的所有决策实体工作负载RMS值

平台合并后当前的决策实体数量为Dnow-1,计算此时决策实体工作负载的RMS值为

(16)

步骤3建立备选平台合并方案集

计算合并后工作负载的RMS值后,根据RMS(h,k)矩阵中的结果按升序进行排列,生成备选合并方案集M={1-best, 2-best, …,m-best},其中1-best对应平台合并后RMS值最小的合并选项(r1,s1),2-best对应平台合并后RMS值次小的合并选项(r2,s2),集合M中包含了m个互不相同的备选平台合并方案。

步骤4确定最佳合并选项

分别令当前层的平台合并方案为集合M中的p-best(p=1,2,…,m),后续聚类过程采用贪婪策略得到最终的平台聚类方案,比较m个不同方案最终的工作负载RMS值,选择使最终聚类RMS值最小的平台合并选项(r,s)作为当前层的平台合并方案。若Dnow=Dstop,则合并结束,否则Dnow=Dnow-1,重复步骤1。

2.3 合并过程中的变量更新法则

(1) 两个决策实体DMr与DMs合并形成新的决策实体DMG,更新平台与决策实体的隶属关系、任务与决策实体的执行关系:

xGj=max(xrj,xsj)

(17)

uGi=max(uri,usi)

(18)

(2) 更新其他决策实体与新决策实体DMG之间的协作工作负载:

R(m,G)=R(m,r)+R(m,s)-Δ(m,r,s)

(19)

(3) 更新合并后的决策实体DMG的总工作负载CW(G):

CW(G)=CW(r)+CW(s)-

(20)

(4) 更新其他决策实体DMm的总工作负载CW(m):

CW(m)=CW(m)-WE·Δ(m,r,s)

(21)

(5) 计算合并后的决策实体总工作负载的RMS值:

(22)

3 算例分析

3.1 特殊算例分析

本文选用文献[16]中的联合作战的战役想定作为特殊算例,对基于rollout策略下的层次聚类法的可行性和有效性进行验证。在该算例中,任务数量I=18,平台数量P=20,具体的平台、任务属性详细描述见参考文献[16]。该战役想定中的平台调度方案的甘特图(平台与任务的匹配关系在聚类开始前是已知的输入信息)如图3所示。

图3 平台调度方案甘特图Fig.3 Gantt chart of platform scheduling scheme

针对该算例,作以下仿真实验:

在基于rollout策略下的层次聚类法的参数设置中,内部工作负载与外部工作负载分别为WI=1、WE=1,决策实体的数量D=5,平台备选合并方案个数m的取值为m=1,2,…,10,得到在该方法下的基于最小RMS合并准则的决策实体的工作负载RMS值(问题模型的目标函数)与m值关系的变化曲线,如图4所示。由图4可知,随着m值的增大,聚类后工作负载的RMS值将减小,当m>3时,RMS值趋于稳定,随着m值继续增大RMS值稳定在249.238 8。

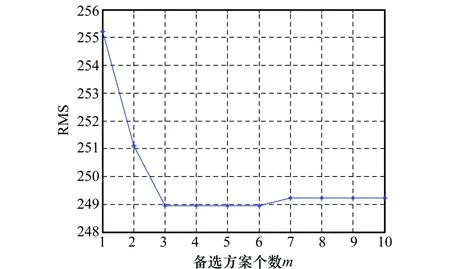
图4 RMS值随备选方案个数m的变化曲线Fig.4 RMS value with change of scheme number m

通过对仿真过程的分析能得出,当m的取值为3～6时,由11个平台分组聚类为10个平台分组的过程中产生了使RMS值达到最小值248.937 7的聚类方案,因此最终聚类后工作负载的RMS值为248.937 7。而当m>6时,在12个平台分组聚类为11个平台分组时产生能使工作负载RMS值达到最小值249.238 8的平台合并方案,后续的逐层的合并方案中将不再产生使RMS值小于该值的合并方案,因此当m>6时,工作负载稳定在249.238 8。实验结果说明,rollout策略下的层次聚类法具有可行性,能改善最终聚类的效果。

为验证该方法的优越性,令平台备选方案个数m=4,其余参数不变,与传统贪婪策略下的层次聚类法[10]在基于最小RMS的合并规则下对所得聚类方案进行对比,从每个决策实体的工作负载、聚类后的RMS值以及方差3个方面进行比较分析,最终的聚类结果如表1、表2所示。

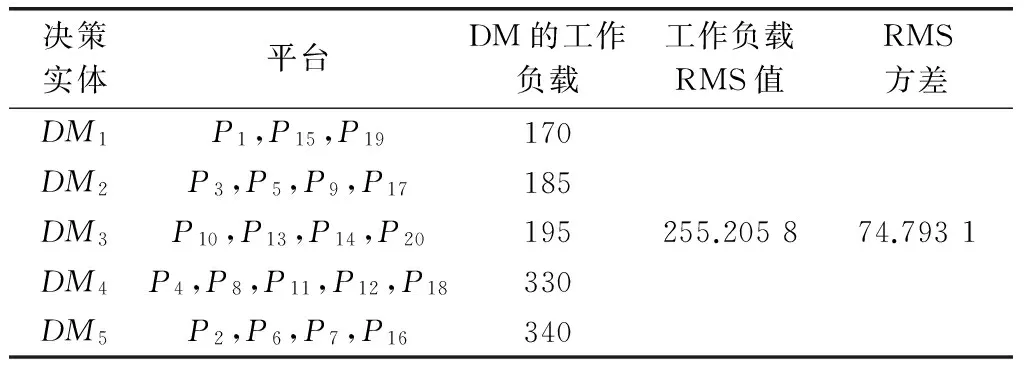
表1 贪婪策略下的层次聚类结果

表2 基于rollout策略下的层次聚类

由表1、表2可知,当决策实体数量为5时,对比贪婪策略下的层次聚类法与基于rollout策略的层次聚类法的聚类方案,决策实体工作负载的最大值由340降低至300,决策实体工作负载的最小值由170提高至185,RMS方差整体降低了25.457 6,表明每个决策实体的工作负载更加均衡,并且问题的目标函数值更小,验证了该方法具有有效性和优越性。

为了验证该方法的适用性,设置不同的工作负载系数进行仿真实验分析。令外部工作负载系数WE=1,设置内部工作负载系数分别为WI=1,2,3,4,在这4种不同负载系数情况下,决策实体的数量D的取值为D=1,2,…,8,分别使用一般层次聚类法和基于rollout策略的层次聚类法(令m=4)在基于最小RMS的合并规则下生成平台聚类方案,得到D个决策实体工作负载的RMS值在不同负载系数下的变化曲线,如图5所示。

图5 不同工作负载系数下RMS值随决策实体数量D值变化曲线图Fig.5 RMS value with change of decsion makes’ number D under different work load factor

由图5中的4幅曲线变化图可知,在不同外部工作负载条件下,使用rollout策略下的层次聚类法都能得到优于一般层次聚类法的聚类结果,该方法下的工作负载RMS值普遍小于一般层次聚类法的RMS值。并且决策实体的数量D越少,基于rollout策略的层次聚类法所得到的聚类方案的效果越好,该结论体现了本文所提方法的优越性,也说明该方法在不同工作负载系数下的适用性。

3.2 一般算例分析

为进一步验证基于rollout策略的层次聚类法对聚类结果具有改善效果,本文将引入一般算例进行仿真分析。设计一般案例的任务数量I=18,平台数量P=20,任务处理时间和不同任务设定下的平台-平台匹配关系均在所引用特殊算例的基础上通过蒙特卡罗方法随机生成。分别使用一般层次聚类法和基于rollout策略的层次聚类法计算聚类方案工作负载的RMS值并进行对比分析,以一般层次聚类法打得到的RMS值作为基准,对比算法改进前后得到的RMS值相对于该基准的优化率(本文优化率指当前算法与一般层次聚类法目标函数值的比值,体现优化程度),通过200次蒙特卡罗仿真实验得到的优化率统计盒须图对比如图6所示。由图6中的两种不同算法下的优化率盒须图可知,采用基于rollout策略的层次聚类法所得到的优化率平均值为1.083 1,使用该方法得到的优化率普遍大于一般层次聚类法。因此对于该聚类问题,本文所提出的基于rollout策略的层次聚类法在统计意义上要优于一般层次聚类法,表明使用该方法能够得到更优的平台聚类方案,充分体现了使用方法的优越性。

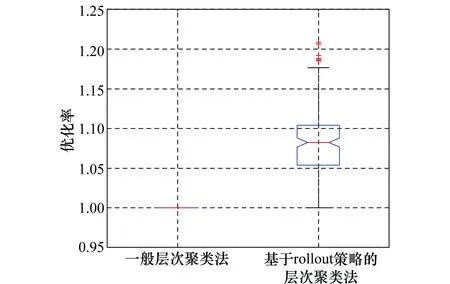
图6 蒙特卡罗仿真两种算法优化率盒须图Fig.6 Boxplot of different algorithm optimization rate under Monte Carlo simulation

4 结 论

本文提出了一种改进的传统C2组织平台与决策实体配置求解方法,针对一般的层次聚类法在聚类时每一层平台合并均采用了贪婪策略可能导致聚类结果无法达到全局最优的情况,提出rollout策略对层次聚类过程进行改进,在每一层合并选项确定前生成该层的m个平台合并备选方案,根据最小RMS合并准则通过rollout策略选择当前层的最佳合并项进行合并,聚类直至平台分组数量与决策实体个数相等时结束。通过特殊案例分析可知,基于rollout策略的层次聚类法可以有效的从整体上降低决策实体的工作负载,并且能进一步均衡决策实体之间的工作负载,减小每个决策实体工作负载之间的差异,使最终得到的聚类方案更加符合实际需求,最后再通过一般案例进一步验证了该方法的适用性与优越性。

工作负载的定义方式将影响最终的聚类方案的生成,不同的定义产生不同的决策实体与平台之间的指控关系,因此充分考虑战场环境的综合因素,从作战任务难度、作战激烈程度等方面综合考虑对工作负载进行测度,会使工作负载的设计更加符合实际需求。同时,决策实体的差异性、决策实体的知识约束也是会对平台聚类结果产生影响的重要因素,后续工作过程中将对上述问题进一步研究。

参考文献：

[1] BUI H, HAN X, MANDAL S, et al. Optimization-based decision support algorithm for a team-in-the-loop planning experiment[C]∥Proc.of the IEEE International Conference on Systems, Man, and Cybernetics, 2009: 4685-4689.

[2] 阳东升, 张维明, 刘忠, 等. 指控组织设计方法[M]. 北京: 国防工业出版社, 2010: 161-189.

YANG D S, ZHANG W M, LIU Z, et al. Designing of command and control organization[M]. Beijing: Nation Defense Industry Press, 2010: 161-189.

[3] HAN X, MANDAL S, PATTIPATI K R, et al. An optimization-based distributed planning algorithm: a blackboard-based colla-borative framework[J]. IEEE Trans.on Systems, Man, and Cybernetics-Part A:Systems and Humans,2017,48(6):673-684.

[4] 孙昱,姚佩阳,张杰勇.C2组织信息结构效能测度及综合评估[J]. 系统工程与电子技术,2015,37(6): 1313-1318.

SUN Y, YAO P Y, ZHANG J Y. Measurement and comprehensive evaluation of C2 organizational information structure efficiency[J]. Systems Engineering and Electronics, 2015, 37(6): 1313-1318.

[5] 周翔翔, 姚佩阳, 尹忠海. 指挥决策实体层次结构设计方法[J]. 电光与控制, 2012, 19(2): 68-72.

ZHOU X X, YAO P Y, YIN Z H. A method for design of command decision-making entity’s hiberarchy architecture[J]. Electronics Optics & Control, 2012, 19(2): 68-72.

[6] SCHEIDT D, SCHULTZ K. On optimizing command and control structures[C]∥Proc.of the 16th International Command and Control Research Symposium, 2011: 1-10.

[7] LEVCHUK G M, LEVCHUK Y N, LUO J, et al. Normative design of organizations—Part Ⅰ: mission planning[J]. IEEE Trans.on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2002, 32(3): 346-359.

[8] LEVCHUK G M, LEVCHUK Y N, LUO J, et al. Normative design of organizations—Part Ⅱ: organizational structure[J]. IEEE Trans.on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2002, 32(3): 360-375.

[9] 刘宏芳, 阳东升, 刘忠, 等. 兵力编成裁剪算法研究:决策节点裁剪[J]. 系统工程与理论实践, 2007, 27(5): 106-112.

LIU H F, YANG D S, LIU Z, et al. Research on algorithm of tailoring military force tailoring nodes of decision-making[J]. Systems Engineering-Theory & practice,2007,27(5):106-112.

[10] 张杰勇,姚佩阳.C2组织决策实体配置问题建模与求解方法[J].系统工程与电子技术,2012,34(4):737-742.

ZHANG J Y, YAO P Y. Model and solving method of collocating problem of decision-makers in C2 organization[J]. Systems Engineering and Electronics, 2012, 34(4): 737-742.

[11] 吴瑞杰,孙鹏,孙昱,等.自适应量子遗传算法在指挥控制结构设计中的应用[J].计算机应用与研究,2016,33(7):113-119.

WU R J, SUN P, SUN Y, et al. Self-adaptation quantum genetic algorithm used in design of command and control structure[J]. Application Research of Computers, 2016, 33(7): 113-119.

[12] 孙昱, 姚佩阳, 吴吉祥, 等. 兵力组织扁平化指挥控制结构设计方法[J]. 系统工程与电子技术, 2016, 38(8): 1833-1839.

SUN Y, YAO P Y, WU J X, et al. Design method of flattening command and control structure of army organization[J].Systems Engineering and Electronics,2016,38(8):1833-1839.

[13] TU F, PATTIPATI K R. Rollout strategies for sequential fault diagnosis[J]. IEEE Trans.on Systems Man & Cybernetics-Part A: Systems & Humans, 2002, 33(1):86-99.

[14] TIAN X, BAR-SHALOM Y, PATTIPATI K R. Multi-step look-ahead policy for autonomous cooperative surveillance by UAVs in hostile environments[C]∥Proc.of the 37th IEEE Conference Decision Control, 2008, 16(5): 2438-2443.

[15] HAN X, BUI H, MANDAL S, et al. Optimization-based decision support software for a team-in-the-loop experiment: asset package selection and planning[J]. IEEE Trans.on Systems, Man, and Cybernetics-Part A:Systems and Humans,2013,44(3): 237-251.

[16] YU F, TU F, PATTIPATI K R. A novel congruent organizational design methodology using group technology and a nested genetic algorithm[J]. IEEE Trans.on Systems, Man, and Cybernetics-Part A: Systems and Humans,2005,36(1):5-18.