基于进化粒子滤波的数据域直接跟踪方法

逯志宇, 巴 斌, 任衍青, 王大鸣

(信息工程大学信息系统工程学院, 河南 郑州 450001)

0 引 言

目标跟踪是对目标位置和速度的实时估计,无论是在民用领域还是军事领域,都是不可或缺的重要技术。尤其随着航空航天事业的蓬勃发展,以及现代战争信息化的转变,运动目标位置与速度的实时估计和预测具有重要研究价值,已成为一个十分活跃的研究方向[1]。

传统跟踪方法首先利用接收信号估计含有目标位置信息的到达时间(time of arrival, TOA)[2]、到达角度(angle of arrival, AOA)[3]、到达时间差(time difference of arrival, TDOA)[4]或到达频率差(frequency difference of arrival, FDOA)[5]等位置参数,然后通过求解这些参数构成的跟踪方程获得目标运动轨迹。由于跟踪方程非线性较强,在目标位置和速度的联合估计中面临高维搜索问题,为此文献[6]提出了一种加权两步最小二乘算法对定位方程进行求解,然后利用卡尔曼滤波(Kalman filtering, KF)方法对估计结果进行平滑得到运动轨迹。虽然这种方法简单易于实现,但是在低信噪比条件下性能恶化严重,跟踪效果不佳。为了解决此问题,扩展卡尔曼滤波(extended KF, EKF)被引入到跟踪系统中[7],不需要求解跟踪方程,而是根据位置参数对目标运动状态进行实时估计,相对KF方法具有更好的性能。但是,EKF算法利用泰勒级数展开近似非线性函数,并且只保留了一阶项,在低信噪比下会带来较大误差,甚至滤波发散[8]。针对EKF算法的缺点,很多改进算法被提出,如无损卡尔曼滤波(unscented Kalman filter, UKF)[9]、积分卡尔曼滤波(quadrature Kalman filter, QKF)[10]、容积卡尔曼滤波(cubature Kalman filtering, CKF)[11]、粒子滤波(particle filter, PF)[12]等,这些算法在非线性函数拟合上能够达到更高阶的近似,跟踪性能不断提升。

虽然经过算法改进,传统两步跟踪算法的精度不断提高,但这种跟踪方法在本质上仍然存在两点不足:一是在参数估计阶段忽略了观测站之间的联系,各观测站之间参数估计过程相互独立,并未考虑定位参数来自于同一目标这一先验信息,损失了部分位置信息;二是第一步参数估计将引入处理误差,误差的传递和累积不可避免,导致第二步跟踪精度受限。因此两步方法是次优的,不能获得最佳的估计精度[13]。与之相比,近些年被提出的直接定位(direct position determination, DPD)算法不需要参数估计和位置解算分步计算,而是基于采样信号直接估计目标位置,避免了两步定位算法的缺点,能够获得更好的定位效果,已得到广泛的研究[14-19]。

文献[20-21]首先详细阐述了DPD算法的基本原理,并给出了利用角度和时延信息的最大似然估计方法。针对最大似然估计高复杂度问题,文献[22]提出了子空间数据融合DPD算法,文献[23-24]提出了最小方差无失真响应(minimum variance distortionless response, MVDR)算法,均降低了参数估计维度,减轻了计算压力。考虑观测站运动场景,文献[25]提出了异步观测条件下的多运动站DPD算法,文献[26]提出了基于时间和多普勒信息的DPD算法。将数据域直接位置解算思想引入到目标跟踪领域,以基于TOA[27]、TDOA[28]和FDOA[29]等信息的DPD算法为基础,文献[30-31]提出了一种目标直接跟踪(direct trajectory determination, DTD)算法,给出了利用时延和多普勒频率信息的算法原理,证明了DTD算法性能优于传统两步跟踪算法。然而上述文献利用了离散时延和多普勒信息,引入量化误差,在采样率较低时严重影响跟踪精度,性能仍有待进一步提高。

综上所述,为了进一步提高目标跟踪性能,本文提出了一种利用连续时延和多普勒信息的直接跟踪算法。与现有文献相比,本文的贡献在于,进一步提高了目标直接跟踪精度,并利用进化PF方法提高跟踪收敛速度,使算法更具实用价值。同时,本文还推导了所提跟踪模型的克拉美罗下界(Cramer-Rao lower bound, CRLB),给出了基于直接数据域跟踪的误差界限。

1 数据域直接跟踪模型

设xk为目标发送的信号,假设信号模型为

x(t)=s(t)ej2πfct

(1)

式中,fc是载频;s(t)是信号的包络。设采样点数为Nk,第l个观测站在第k次观测时得到采样信号为

nk=1,2,…,Nk

(2)

(3)

(4)

(5)

Bτl,k(ok)=diag{exp(-j2π/Nknkτl,k(ok)/Ts)}

(6)

令

Bvl,k(ok)=diag{exp(j2πTsvl,k(ok)nk)}

(7)

联合式(5)～式(7),令

Hl,k(ok)=Bvl,k(ok)VHBτl,k(ok)V

(8)

Hl,k(ok)包含了目标的位置和速度参数,由于利用了时间和多普勒信息,称之为时频观测矩阵。因此可将接收信号表示为

rl,k=Bvl,k(ok)VHBτl,k(ok)Vxk+wl,k=Hl,k(ok)xk+wl,k

(9)

令

(10)

则所有观测站的接收信号联合表示为

rk=Hk(ok)xk+wk

(11)

通过上述方法,使用连续时间信息避免了量化误差的引入,将进一步提升跟踪性能。系统基于接收信号的状态方程和观测方程可以表示为

ok+1=Fok+σk

(12)

rk=H(ok)xk+wk

(13)

式中,F为状态转移矩阵;σk为零均值高斯白噪声,表示目标状态的抖动误差,其协方差矩阵为

(14)

2 PF直接跟踪算法

在两步跟踪算法中,时间和频率等参数作为观测量,可采用的滤波方法较多,如EKF、UKF、CKF、PF等,并且在高信噪比条件下,性能相差并不明显。但是在直接跟踪方法中,由于观测量是接收信号,非线性更强,导致EKF、UKF等方法效果并不理想,所以在直接跟踪中选择能够处理更强非线性问题的PF算法较为合理。

(15)

根据大数定理,当M足够大时,p(ok|rk)将收敛于真实的后验概率。粒子权重计算公式为

(16)

(17)

(18)

(19)

(20)

根据式(11),利用最小二乘准则,xk可表示为

(21)

将式(21)代入式(20),可以得到

(22)

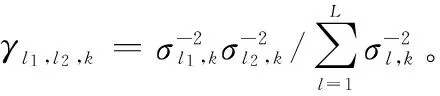
(23)

从而得到估计结果为

(24)

根据式(17),下一时刻的采样粒子为

(25)

为了解决PF存在的退化和贫化问题,基于遗传进化思想的粒子空间构造(evolutionary particle filter, EPF)方法较为常用,即对某些粒子进行变异来增加粒子的多样性,然后根据一定的准则选择出优质粒子进行下一代的计算。下面给出一种进化策略,由变异操作和选择方法组成。在每一代滤波过程中,根据式(25)产生的新粒子,利用式(26)进行如下操作。

(26)

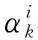
基于数据域的运动目标直接跟踪算法相比于两步跟踪算法精度得到了提升。针对其高度非线性特点,本节给出了利用进化PF的迭代求解算法,与文献[31]所用的标准PF相比,目标跟踪效率得到提升,仿真实验中将进一步证明所提算法的有效性。结合上述原理分析,可以将基于EPF的直接跟踪(EPF-DTD)算法概括如下:

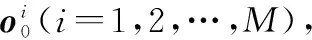
步骤2根据式(26)对采样粒子进行变异操作,得到新的粒子集;

步骤5根据权重大小对粒子进行筛选,选择权重较大的一半作为优质粒子;

步骤6利用优质粒子,根据式(24)得到本次迭代的目标状态估计;

步骤7利用轮盘赌方法对粒子进行重采样,根据式(25)得到下一代粒子;

步骤8如果迭代终止,将本次结果作为输出,否则跳转步骤2进行下一次迭代。

3 CRLB

CRLB给出了无偏估计量的方差下限,对研究模型的理论性能具有重要意义。本节将推导一种所提直接跟踪模型CRLB的递归求解算法,给出目标状态的估计性能界限。

设P(r,o)是(r,o)联合概率分布,则费希尔信息矩阵(Fisher information matrix, FIM)可以表示为

(27)

式中,Δ为偏导算子,表示为

(28)

(29)

则o2的FIM矩阵可以表示为

(30)

式中,J2也称为o2的信息子矩阵。

Pk+1=PkP(rk+1|ok+1)P(ok+1|ok)

(31)

从而k时刻的FIM矩阵可以表示为

(32)

进一步,在k+1时刻可以得到

(33)

根据式(31),可以得到

lgPk+1=lgPk+lgP(rk+1|ok+1)+lgP(ok+1|ok)

(34)

所以式(33)可以表示为

(36)

令

(37)

显然,有式(38)成立

(38)

从而有

(39)

根据式(30),第k+1时刻对新增ok+1的信息子矩阵为

(40)

化简可得

(41)

根据式(32)有

(42)

所以结合式(41)和式(42),可以得到CRLB的递推公式为

(43)

结合第1节给出的跟踪模型,式(37)可以表示为

(44)

式中

(45)

表示在k+1时刻状态ok+1独立的FIM矩阵,根据式(11)和式(27),有

(46)

利用链式法则,可以得到

(47)

式中

(48)

(49)

(50)

(51)

4 仿真分析

为了验证所提算法的性能,本节将对EPF-DTD算法的跟踪精度和CRLB进行仿真,并与文献[31]中提出的时延和多普勒信息离散化直接跟踪算法(简记为PF-DTD)和基于时频差的两步跟踪算法(简记为PF-TDOA/FDOA)进行对比。

为了说明各算法的跟踪性能,在信噪比20 dB条件下,得到算法的跟踪效果如图1所示,运动方向由下向上,跟踪误差变化曲线如图2所示。可以看出,3种算法在经过短暂的调整后都能以一定的误差跟踪目标,其中PF-DTD算法的跟踪精度和速度比PF-TDOA/FDOA算法略有提升,证明直接跟踪方法具有一定优势。但是由于PF-DTD算法对时延做了量化处理,引入了部分量化噪声,直接跟踪方法的性能优势并未完全展现。EPF-DTD算法避免了量化问题,并且对PF算法做了改进,所以在跟踪速度和精度上相对于PF-DTD算法具有较大的提高。在图1的放大图中可以看到,当目标做折线运动时,EPF-DTD能够在短时间内快速的跟踪目标运动变化,并且误差能够保持在较低水平,而PF-DTD和PF-TDOA/FDOA算法的跟踪速度相对较慢,误差变化较大,进一步证明了本文所提算法的有效性。

图1 不同算法位置跟踪过程Fig.1 Position tracking of different algorithms

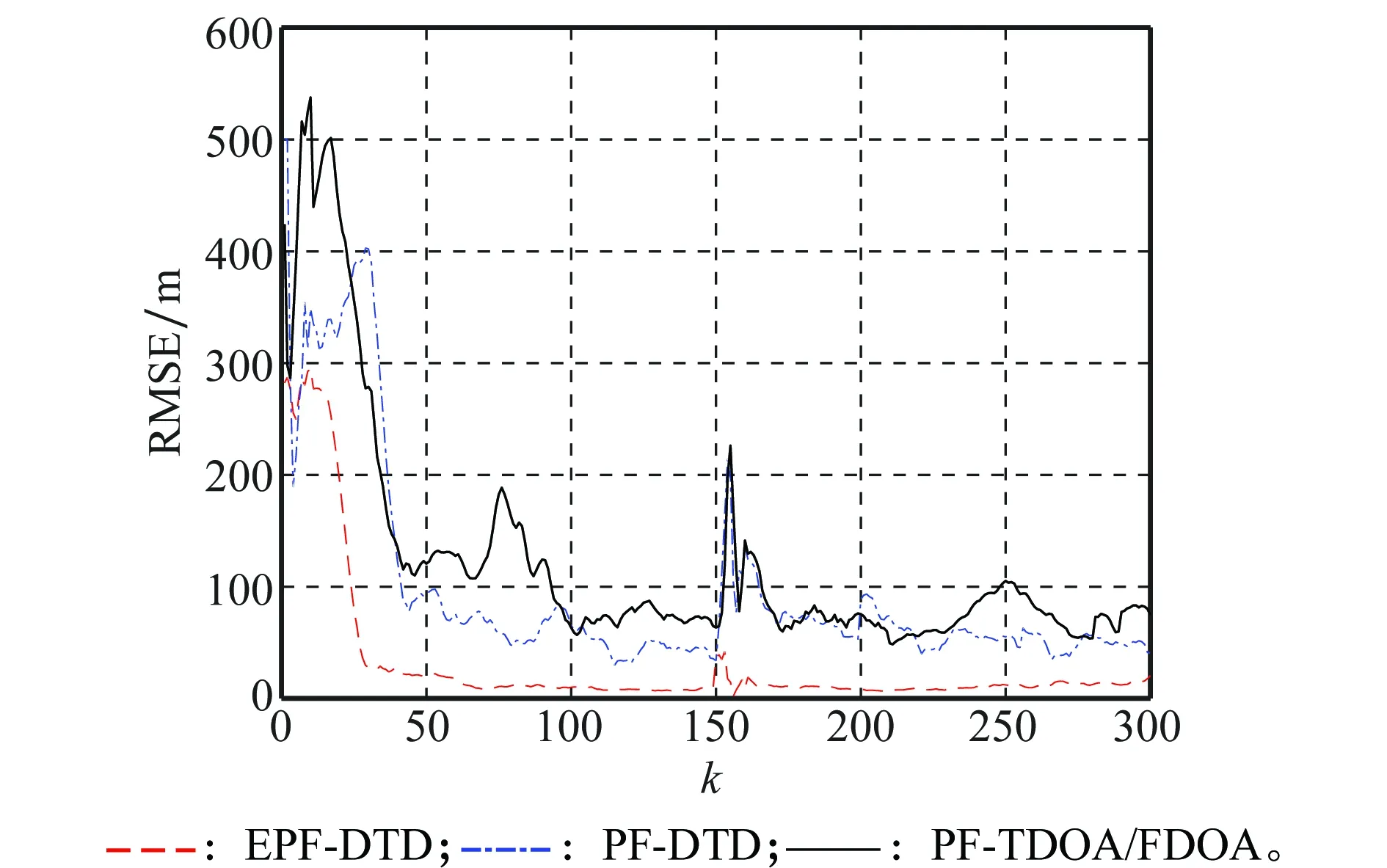
图2 不同算法位置均方根误差Fig.2 Root mean square error (RMSE) of location for different algorithms

在相同条件下,图3和图4是速度跟踪效果以及误差曲线。从图中可以看出,PF-DTD和PF-TDOA/FDOA算法的速度跟踪能力大致相同,且误差较大,而EPF-DTD算法能够在短时间内达到较好的跟踪效果,最终误差能够维持在较低水平。当目标做折线运动时,EPF-DTD可以快速跟踪目标速度变化,而PF-DTD和PF-TDOA/FDOA算法的跟踪效果相对较差。出现这种现象的原因是,速度的跟踪能力取决于FDOA信息的处理能力,PF-TDOA/FDOA算法对FDOA参数的估计精度较低,影响了跟踪精度,PF-DTD算法中的量化误差也间接影响了速度的跟踪效果,而EPF-DTD算法避免了上述问题,因此速度跟踪效果较为理想。

为了说明EPF-DTD算法的跟踪性能,得到其CRLB随迭代次数k和信噪比的变化曲线如图5所示。可以看出,随着信噪比的增加,算法的跟踪精度不断提高,证明了算法的跟踪性能。随着迭代次数的增加,在高信噪比条件下,跟踪精度相应提高,并且能够快速收敛；但是在较低信噪比条件下,收敛速度变慢,需要较长时间才能够稳定。原因在于,一方面,观测信号较弱时,无法快速消除先验假设引进的误差；另一方面,由于目标运动,不同位置所能达到的理论估计精度会有波动,在信噪比较低时会对跟踪性能带来影响。

图4 不同算法速度跟踪误差Fig.4 Speed tracking error of different algorithms

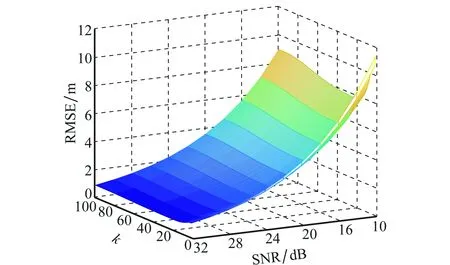
图5 EPF-DTD算法的CRLB随迭代次数k和信噪比的变化曲线Fig.5 CRLB of EPF-DTD algorithm over signal-to-noise ratio (SNR) and k

进一步,令迭代次数k=100,对各算法进行50次蒙特卡罗仿真实验,将不同算法位置估计误差随信噪比的变化趋势进行对比,其结果如图6所示。可以看出,PF-DTD算法与PF-TDOA/FDOA算法在高信噪比条件下性能相近,但在低信噪比条件下,PF-DTD算法性能有明显提升,证明了直接跟踪思想的正确性。相比于PF-DTD和PF-TDOA/FDOA算法,本文提出的EPF-DTD算法在跟踪精度上有较大地提升,证明算法构造连续时延信息模型以及利用EPF算法求解的有效性。同时可以看到,EPF-DTD算法能够接近CRLB,由于实际滤波中粒子数量有限,与CRLB仍有微小距离,但在高信噪比条件与CRLB基本吻合。

图6 不同算法性能随信噪比变化曲线Fig.6 RMSE of position versus SNR of different algorithms

为了验证不同采样频率对算法的影响,在fs=1 MHz和fs=0.5 MHz条件下对EPF-DTD算法和PF-DTD算法的跟踪误差进行了仿真,结果如图7所示。可以看出,采样频率对EPF-DTD算法的影响较小,不同采样率下算法的跟踪性能相近。而PF-DTD算法由于受量化误差的影响,当采样频率下降时,性能下降较快。结果说明，本文所提EPF-DTD算法有效避免了PF-DTD算法的量化误差问题,可以在较小采样率下获得优异的跟踪性能。

图7 不同采样频率时算法跟踪误差对比Fig.7 Comparison of tracking error at different sampling rates

5 结 论

本文针对目标跟踪问题,提出一种利用连续时延信息,并基于进化PF的直接跟踪方法,给出了详细的模型构建、原理分析和CRLB推导过程。所提算法利用观测站接收信号直接进行目标跟踪,具有比两步定位更高的跟踪精度,同时进化PF方法提高了算法的计算效率。仿真实验给出了所提算法与其他算法的性能对比,证明了算法能够获得更好的跟踪性能,具有一定实用价值。

参考文献：

[1] 杨峰,张婉莹.一种多模型贝努利粒子滤波机动目标跟踪算法[J].电子与信息学报,2017, 39(3):634-639.

YANG F, ZHANG W Y. Multiple model bernoulli particle filter formaneuvering target tracking[J]. Journal of Electronics & Information Technology, 2017, 39(3): 634-639.

[2] 冷雪冬, 巴斌, 逯志宇,等. 基于回溯筛选的稀疏重构时延估计算法[J]. 物理学报, 2016, 65(21): 701-710.

LENG X D, BA B, LU Z Y, et al. Sparse reconstruction time delay estimation algorithm based on backtracking filter[J]. Acta Physica Sinica, 2016, 65(21): 701-710.

[3] XU J, MA M D, LAW C L. AOA cooperative position localization[C]∥Proc.of the IEEE Global Telecommunications Conference on Signal Processing, 2008: 1-5.

[4] CHAN Y T, HO K C. Joint time-scale and TDOA estimation: analysis and fast approximation[J]. IEEE Trans.on Signal Processing, 2005, 53(8): 2625-2634.

[5] 严航, 朱珍珍. 基于积分抽取的时/频差参数估计方法[J].宇航学报, 2013, 34(1):99-105.

YAN H, ZHU Z Z. Fast algorithm for joint estimation of DTO and DFO based on integrate-and-dump filters[J]. Journal of Astronautics, 2013, 34(1): 99-105.

[6] HO K C, XU W W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Trans.on Signal Processing, 2004, 52(9): 2453-2463.

[7] LIN C M, HSUEH C S. Adaptive EKF-CMAC-based multisensor data fusion for maneuvering target[J]. IEEE Trans.on Instrumentation and Measurement, 2013, 62(7): 2058-2059.

[8] GUSTAFSSON F, HENDEBY G. Some relations between extended and unscented Kalman filters[J]. IEEE Trans.on Signal Processing, 2012, 60(2): 545-555.

[9] JULIER S J, UHLMAN J K. Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3):401-422.

[10] IENKARAN A, SIMON H, ROBERT J E. Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature[J]. Proceedings of the IEEE, 2007, 95(5): 953-977.

[11] 逯志宇, 王大鸣, 王建辉, 等. 基于时频差的正交容积卡尔曼滤波跟踪算法[J]. 物理学报, 2015, 64(15): 25-32.

LU Z Y, WANG D M, WANG J H, et al. A tracking algorithm based on orthogonal cubature Kalman filter with TDOA and FDOA[J]. Acta Physica Sinica, 2015, 64(15): 25-32.

[12] GUSTAFSSON F. Particle filter theory and practice with positioning applications[J]. IEEE Aerospace and Electronic Systems Magazine, 2010, 25(7): 53-81.

[13] BOSSE J, FERRéOL A, LARZABAL P. Performance analysis of passive localization strategies: direct one step approach versus 2 steps approach[C]∥Proc.of the IEEE Statistical Signal Processing Workshop, 2011: 701-704.

[14] BAR-SHALOM O, WEISS A J. Direct emitter geolocation under local scattering[J].Signal Processing,2015,117:102-114.

[15] WANG D, ZHANG G, SHEN C Y, et al. A direct position determination algorithm for constant modulus signals with single moving observer[J]. Acta Aeronautica et Astronautica Sinica, 2016, 43(5): 1622-1633.

[16] WANG D, ZHANG R J, ZHANG T. A direct position determination approach for radio emitters in presence of mutual coupling[J]. Acta Electronica Sinica, 2017, 45(5): 1130-1138.

[17] YIN J X, WU Y, WANG D. Direct position determination of multiple noncircular sources with a moving array[J]. Circuits Systems & Signal Processing, 2017, 36(10): 4050-4076.

[18] LU Z Y, WANG J H, BA B, et al. A novel direct position determination algorithm for orthogonal frequency division multiplexing signals based on the time and angle of arrival[J]. IEEE Access, 2017, PP(99): 1-9.

[19] TIRER T, WEISS A J. Performance analysis of a high-resolution direct position determination method[J]. IEEE Trans.on Signal Processing, 2017, 65(3): 544-554.

[20] WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513-517.

[21] WEISS A J, AMAR A. Direct position determination of multiple radio signals[J]. Eurasip Journal on Advances in Signal Processing, 2005, 2005(1): 37-49.

[22] AMAR A, WEISS A J. A decoupled algorithm for geolocation of multiple emitters[J]. IEEE Trans.on Signal Processing, 2007, 87(10): 2348-2359.

[23] TIRER T, WEISS A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters, 2016, 23(2):192-196.

[24] TZAFRI L, WEISS A J. High-resolution direct position determination using MVDR[J]. IEEE Trans.on Wireless Communications, 2016, 15(9): 6449-6461.

[25] 冯奇,曲长文,周 强. 多运动站异步观测条件下的直接定位算法[J]. 电子与信息学报, 2017, 39(2): 417-422.

FENG Q, QU C W, ZHOU Q. Direct position determination using asynchronous observations of multiple moving sensors[J]. Journal of Electronics & Information Technology,2017,39(2):417-422.

[26] 逯志宇,任衍青,巴斌,等.基于分段信号相关累加的变速度多站联合直接定位方法[J].物理学报, 2017, 66(2):70-79.

LU Z Y, REN Y Q, BA B, et al. An improved direct position determination method based on correlation accumulation of short-time signals with variable velocity receivers[J]. Acta Physica Sinica, 2017, 66(2):70-79.

[27] LI J Z, YANG L, GUO F C, et al. Coherent summation of multiple short-time signals for direct positioning of a wideband source based on delay and Doppler[J]. Digital Signal Processing, 2015, 48(3):58-70.

[28] VANKAYALAPATI N, KAY S, QUAN D. TDOA based direct positioning maximum likelihood estimator and the Cramer-Rao bound[J]. IEEE Trans.on Aerospace and Electronic Systems, 2014, 50(3): 1616-1646.

[29] POURHOMAYOUN M, FOWLER M. Distributed computation for direct position determination emitter location[J]. IEEE Trans.on Aerospace and Electronic Systems, 2014, 50(4): 2878-2889.

[30] SIDI A J, WEISS A J. Tracking of a moving emitter based on delay and Doppler shift using a particle filter[C]∥Proc.of the IEEE Convention of Electrical & Electronics Engineers in Israel, 2010: 001012-001016.

[31] SIDI A Y, WEISS A J. Delay and Doppler induced direct tracking by particle filter[J]. IEEE Trans.on Aerospace & Electronic Systems, 2014, 50(1): 559-572.