基于演化网络模型的箱粒子CPHD群目标跟踪
2018-04-26宋骊平姬红兵
程 轩, 宋骊平, 姬红兵
(西安电子科技大学电子工程学院, 陕西 西安 710071)
0 引 言
弹道导弹目标在飞行过程中会发生弹头弹体分离,且在飞行中段为实现突防目的,会释放大量伴飞诱饵如干扰箔条等,这些干扰目标与真实的导弹弹头将会混杂在一起,形成许多不同的目标群[1]。这些目标群中的目标不仅位置上相互临近,而且运动模式也很相似,并且随着运动的进行不同群间还会不断地发生分裂与合并,这对现有的目标跟踪系统提出了更高的要求[2]。
早期的群目标跟踪算法研究以编队目标[3]等特殊形式的群目标为主,其结论不具有普遍性,难以解决像弹道导弹群目标跟踪等复杂场景的群目标跟踪问题,因此,研究其他通用的群目标跟踪算法具有重要意义。文献[4]提出一种多帧分配(multiple frame assignment,MFA)跟踪算法。文献[5]借鉴传统多目标跟踪算法中的多假设跟踪(multiple hypothesis tracking,MHT)和多帧分配思想,提出一种多假设聚类多帧指派算法。然而,这些传统的基于数据关联的目标跟踪算法的计算量是巨大的,往往难以满足实时性的需求。
最近几年,Mahler提出了随机有限集理论来研究多目标跟踪问题的思路,它将多目标跟踪问题转变为集合意义下的单目标跟踪问题,避免了数据关联,因此一经提出,便得到广泛应用[6-7]。针对传统的多目标跟踪问题,Mahler提出一种概率假设密度(probability hypothesis density,PHD)滤波器[8],随后,又在2007年提出了CPHD滤波器[9],这种滤波器引入了目标的势估计,采用最大后验准则估计目标个数,拥有比PHD更准确的目标数目估计,尤其是在杂波强度比较大的情况下。目前,这些滤波器的具体实现方法主要有高斯混合(Gaussian mixture,GM)实现和序贯蒙特卡罗(sequential Monte Carlo,SMC)实现。上述随机集框架下的多目标跟踪方法的发展为群目标跟踪方法的研究奠定了坚实的基础。文献[10]将GM-PHD滤波方法应用于线性条件下的群目标跟踪问题。文献[11]提出利用群质心状态及其扩散形态来描述群整体状态,并推导出严格的贝叶斯递推方法。文献[2]将群目标的扩散形态建模为椭圆,在线性高斯条件下提出了一种基于椭圆随机超曲面模型(random hypersurface model,RHM)的群目标GM-PHD滤波算法,它可实现对群目标质心和扩散形态的稳定跟踪。文献[12]提出了基于SMC-PHD的部分可分辨的群目标跟踪算法,可在非线性条件下实现对目标质心状态和群扩散形态的稳定跟踪。但上述算法都无法给出群内单个目标的状态和群的演化特性。文献[13]提出一种利用网络图形的形式来描述群结构,将群内目标与周围其他目标联系起来,很好地解决了这一问题。但其群内目标状态估计采用粒子滤波来处理,为获得更准确的估计结果,就需要更多的粒子,这会导致计算量大大增加,不利于群目标的实时跟踪。近年来,箱粒子(box particle, BP)滤波[14]的出现解决了粒子数多,运算量大的问题,逐渐受到了学界的关注。
BP滤波是粒子滤波与区间分析相结合形成的一种广义粒子滤波算法,尤其适合解决目标跟踪问题中的非精确量测情况。文献[15]将BP滤波应用于目标跟踪,针对单目标跟踪问题提出了伯努利BP滤波;之后,文献[16]采用BP实现PHD滤波器,提出了BP-PHD多目标跟踪算法,相比于传统的SMC-PHD多目标跟踪,BP-PHD在保证估计性能的同时,大大降低了算法的运算量。鉴于BP滤波在多目标跟踪中表现出的良好性能,本文采用BP实现CPHD滤波器以降低传统的粒子CPHD(简记为SMC-CPHD)群目标跟踪算法的运算量,并通过演化网络模型实时更新群结构,提出一种基于演化网络模型的BP势概率假设密度(简记为BP-CPHD)群目标跟踪算法。
1 演化网络模型
群目标跟踪主要包括两个方面,一是需要对群内个体目标的运动状态进行估计,二是需要考虑群内不同目标间的相互作用关系,即需要考虑群结构的更新问题。另外,群目标跟踪算法还需要实时处理群目标的一些典型的运动特征,如群的分裂、合并等。演化网络模型用顶点表示不同目标,用边表示不同目标间的关系,可以很好地实现上述目的。
假设有N个目标,则可构成一个顶点的集合V={v1,v2,…,vN},两个目标之间的关系用边E(i,j)=(vi,vj)表示,其中顶点vi包含第i个目标对应的状态xi及其方差Pi,因此群结构的整体可以用G=({v1,v2,…,vN},E)来描述。为了对两个顶点之间是否存在关系进行定量表示,文献[14]通过计算不同目标间的马氏距离与相应门限对比来判定哪些目标属于同一个连通分支,这些目标即构成同一个群。因此,还可以用G={g1,g2,…,gnG}来描述整体的群结构,其中gi代表第i个连通分支,即第i个子群,nG代表G内的子群个数。
群结构更新即是要实现Gk=f(Gk-1,Xk),其中,Gk表示k时刻的群结构,Xk={xk,1,xk,2,…,xk,N}表示k时刻N个目标状态向量的集合,f表示群整体的演化网络模型,具体包括模型起始fI、边的更新模型fEU、顶点合并模型fNI和顶点消除模型fNS。
1.1 模型起始fI
假定k=0时,已知目标个数N及其各自的状态,并用V={v1,v2,…,vN}表示N个目标所构成的顶点集合。计算集合V中任意两个不同顶点vi和vj(i,j=1,2,…,N;i≠j)的马氏距离di,j,并与预设门限ε比较,若di,j<ε,则将对应边(vi,vj)保存在E中,最后得到起始群结构G0=({v1,v2,…,vN},E0)。
1.2 边的更新fEU
由于模型中的顶点表示目标,因此当跟踪场景中目标数较多时,顶点数也会比较多,这就导致计算边的更新时运算量会比较大。为了降低计算量,文献[13]中提出了一种基于双层群结构的边更新模型。构建第二层群结构G′,取每个子群g内目标状态的平均值Og作为子群g的质心状态,并用之代表子群g整体的状态:
(1)
相应地,使用子群g内各目标状态的协方差矩阵的平均值Pg代表子群g整体的协方差矩阵:
(2)
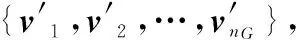
1.3 顶点合并fNI
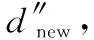
1.4 顶点消除fNS
如果关于顶点vold的信息在一段时间内没有被获得,那么认为顶点vold对应于一个消亡的目标,因此将该顶点及其对应的边分别从顶点集和边的集合中删除。
2 区间分析与BP滤波
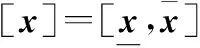
BP滤波是将传统粒子滤波与区间分析相结合而形成的一种适用于非线性条件下的滤波算法。在二维空间中,定义BP为一个矩形区域,该区域面积不为零且大小是可控的,用此BP代替传统的点粒子进行后验概率密度函数的近似,从而实现滤波的方法称为BP滤波[17]。其主要步骤[18]如下:
步骤1输入采样的BP及其对应的权值:
(3)
步骤2依据状态方程进行预测:
(4)
步骤3BP量测更新:
①依据量测方程进行量测预测
(5)
②计算新息
(6)
③似然函数计算
(7)
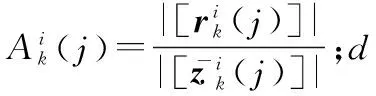
④BP收缩
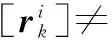
⑤计算归一化权值
(8)
步骤4状态估计
(9)
式中,mid (·)为取BP中心点;
(10)
步骤5BP重采样
(11)
3 BP-CPHD演化网络群目标跟踪
本文使用BP实现CPHD滤波器以解决传统的SMC-CPHD群目标跟踪算法运算量大的问题,同时使用演化网络模型对群结构进行更新,算法的实现框图如图1所示。
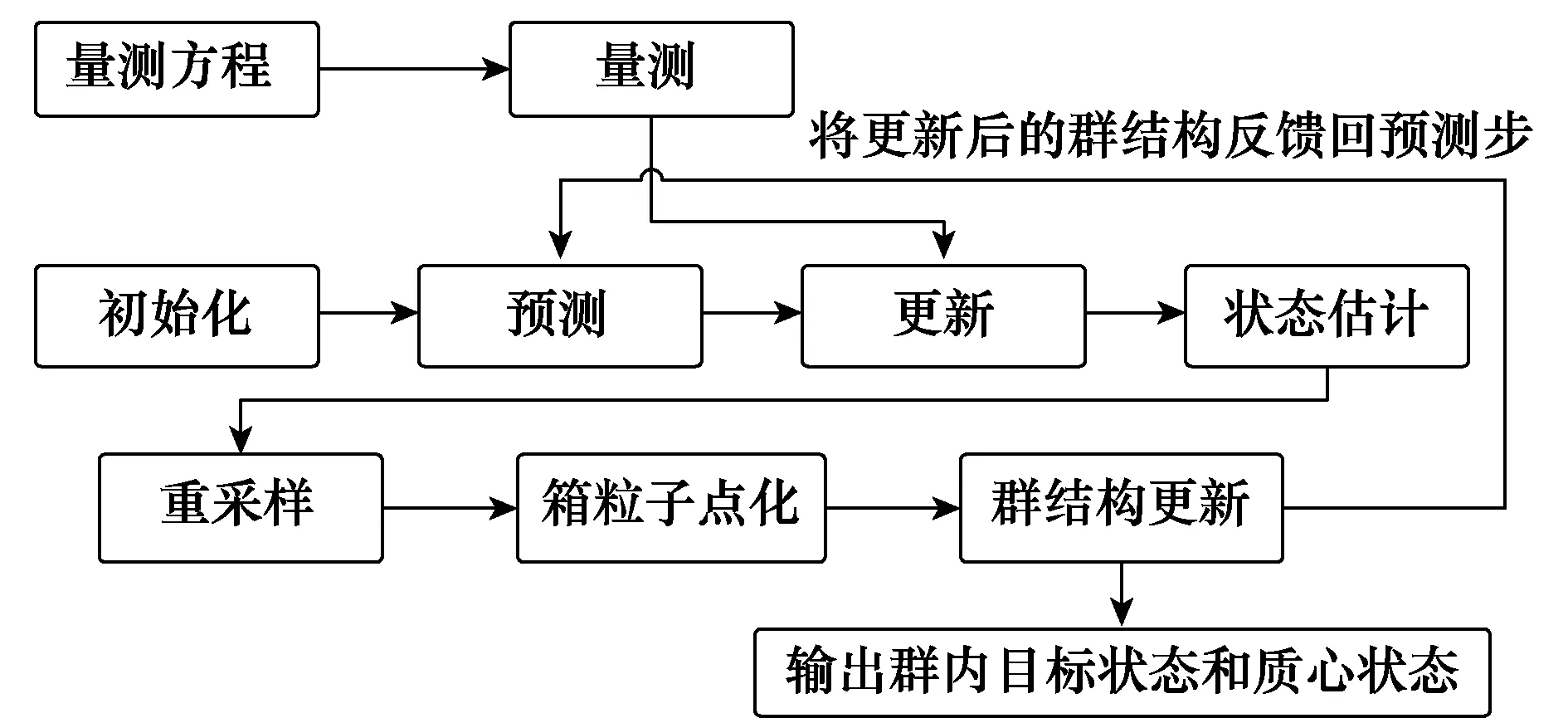
图1 BP-CPHD群目标跟踪算法Fig.1 BP-CPHD group target tracking algorithm
3.1 初始化
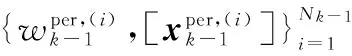

(12)

(13)
式中,Pb,k([x])为新生概率。则初始化BP集合由存活BP集和补入的BP集两部分组成,总的BP集可表示为
=
(14)
k时刻BP总数可以表示为Nk=Nk-1+Nk,new。

3.2 预测
通过状态转移方程进行状态预测,即
(15)
(16)
目标数的势分布的预测方程表示为
(17)
(18)
式中,M为马尔可夫转移矩阵,当雷达扫描率固定不变时,它是一个常量;pb(n)为依据目标的新生模型,从前一时刻k-1到当前时刻k共有n个目标新生的概率[19]。
3.3 更新

(19)
(20)
式中,D和-D分别表示目标被检测与未被检测的速记符号;pd为检测概率。此处,预测与更新的形式类似于SMC-CPHD,但这里用到的似然函数却不同于SMC-CPHD,上述方程所用似然函数计算如下:
(21)
L([Zk]|-D)=
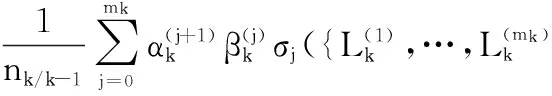
(22)
(23)
(24)
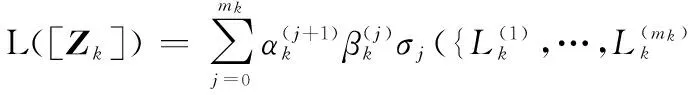
(25)
L([Zk]|n)=
(26)
(27)
(28)
式中,pf(m)为m次虚警的概率;hcp为约束传播算法。

[x]=[x]∩[xz], [y]=[y]∩[yz]
(29)
当不存在与预测箱重叠的量测时,预测箱不约束直接传递[16]。
3.4 重采样
为了防止更新后的BP退化,保持BP的多样性,重采样操作必须被执行。由于BP以区间形式呈现且数目较少,所以与粒子滤波不同,BP重采样既要防止其过分发散,又要避免其过快收敛。因此,在预测步骤中,在前一时刻的量测位置处实时补入新的BP,以解决BP集的多样性问题。另外,新生BP的补入对新生目标也起到了一定的检测作用。
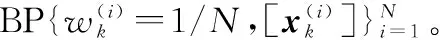
3.5 群结构更新
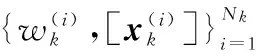
3.6 群目标状态提取
4 仿真结果与分析
此处针对群目标跟踪问题,对群目标运动进行模拟,设计了3组仿真实验以验证本文所提算法的性能,并将之与SMC-CPHD和BP-PHD两种群目标跟踪算法进行对比分析,本文使用最优子模式指派(optimal sub-pattern assignment, OSPA)距离作为滤波性能的评价指标[20]。
4.1 群目标运动模型和量测模型
将群内每个目标的运动模型建模为匀速(constant velocity,CV)模型,其状态方程为
xk=Fxk-1+Γωk
(30)

假设量测空间Z⊆Rnz,那么k时刻第i个目标的点量测zk,i∈Z可以表示为
zk,i=Hxk+νk
(31)
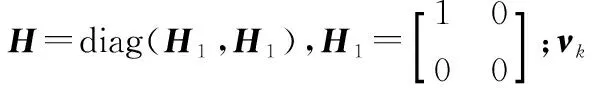
Zk∶Zk={[zk,1],…,[zk,N]}∈F(Z)
式中,F(Z)表示区间量测的子集空间。
最后,将演化网络模型和群内每个目标各自的运动模型联系起来,获得群目标整体的运动模型,经过滤波,便可得到各目标的状态和相应的群结构信息[21]。
4.2 仿真分析
4.2.1 实验1
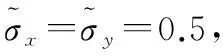
各目标初始运动状态如下:
x1=[-400,20,400,-23]T
x2=[400,-7,470,-23]T
x3=[-400,20,410,-23]T
x4=[405,-7,470,-23]T
x5=[-400,22,-300,15]T
x6=[-405,22,-300,15]T
x7=[-410,22,-300,15]T
x8=[-400,20,0,14]T
另外,目标8在12时刻运动状态变为[~,20,~,-23]T,目标7在30时刻运动状态变为[~,18,~,-15]T,其中,“~”表示目标速度变化时所对应的位置。
图2给出了群目标运动的真实轨迹。目标1和目标3构成了群1(group1),目标8单独成群,构成群2(group2),在第12个时刻与群1发生合并;目标5、目标6和目标7组成的编队构成群3(group3),在第30个时刻发生了群的分裂,即目标7飞出编队;目标2和目标4形成群4(group4)。图中箭头表示各群运动方向。

图2 群目标真实轨迹Fig.2 Group target true trajectories
3种算法的单次蒙特卡罗仿真结果如图3所示。
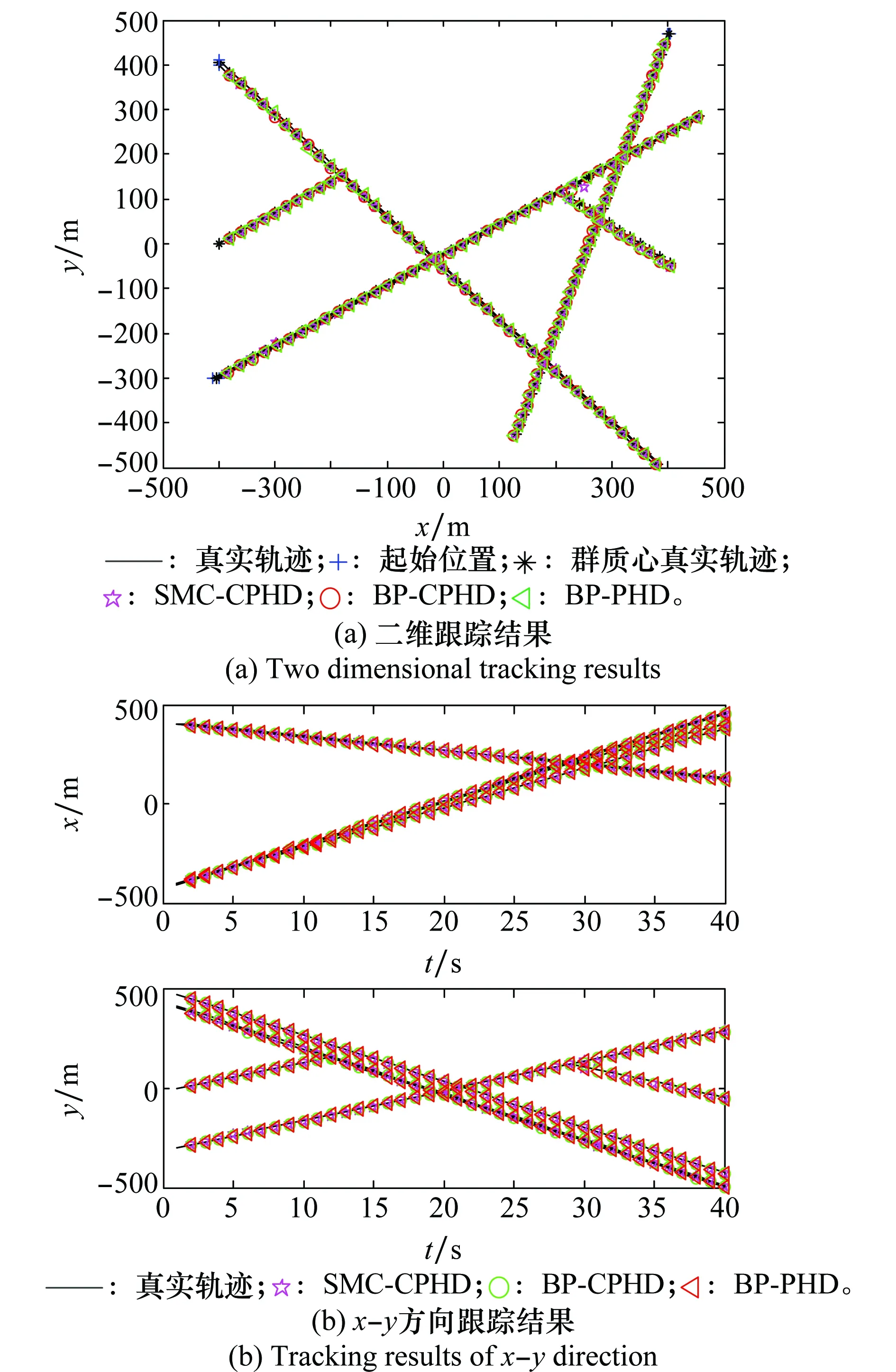
图3 3种算法的跟踪结果Fig.3 Tracking results of three algorithms
为验证3种算法的跟踪效果,本文进行了50次蒙特卡罗仿真。群数目估计结果和平均OSPA距离如图4和图5所示。

图4 群目标势估计Fig.4 Group target cardinality estimation
从图4和图5可以看出,3种滤波算法都取得了较好的跟踪效果,获得了类似的估计性能,然而,相比于传统的SMC-CPHD群目标跟踪算法,本文所提BP-CPHD群目标跟踪算法大幅减少了粒子数,降低了运算量,为群目标的实时跟踪提供了一种良好的方法。3种算法所需粒子数和每个时刻的平均运行时间如表1所示。
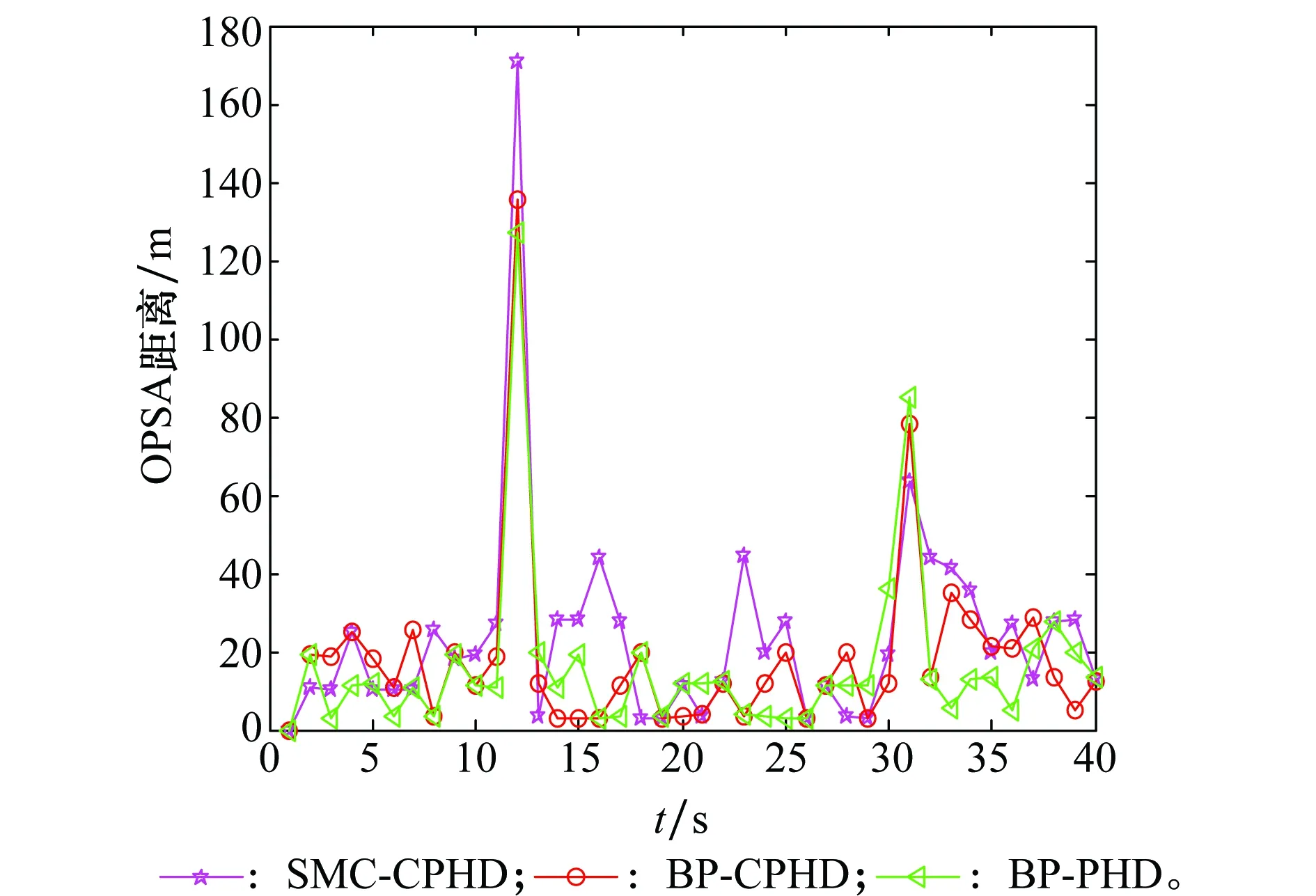
图5 OSPA距离Fig.5 OSPA distance
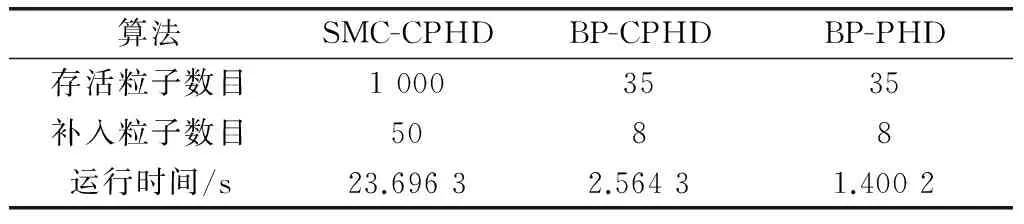
算法SMC-CPHDBP-CPHDBP-PHD存活粒子数目10003535补入粒子数目5088运行时间/s23.69632.56431.4002
另外,在12和31时刻,群目标数估计与真实群目标数相比,波动程度较大,存在着较大的估计误差,这主要是因为在12时刻群目标发生合并,30时刻发生群目标的分裂,这两个时刻群与群之间距离较近,群目标状态提取过程中聚类稳定性较差,导致了不同程度的漏估和过估。
4.2.2 实验2
为验证本文所提算法在强杂波环境下的优越性,此处在实验一的基础上又增设了4组实验,将杂波平均数r分别设置为4、6、8、10,其他条件与实验一完全相同。其平均OSPA距离如图6所示。
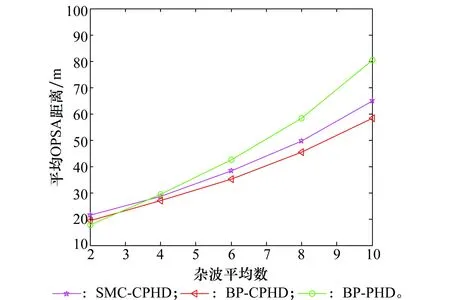
图6 不同杂波强度下平均OSPA距离Fig.6 Averaged OSPA distance versus clutter number
从图6可看出,当杂波平均数为2时,3种算法平均OSPA距离相近且都较小,表明杂波数较少时,三者估计性能相近,都可以取得较好的估计效果。然而,随着杂波平均数的增加,3种算法的平均OSPA距离也随之增加,表明随杂波数增多,3种算法的估计性能都有所下降,但在强杂波环境下,BP-CPHD群目标跟踪算法获得了比其他两种群目标跟踪算法更好的估计性能。
4.2.3 实验3
为验证本文所提算法在低检测概率环境下的跟踪性能,此处在实验1的基础上增设4组实验,将检测概率pd分别设置为0.95、0.90、0.85、0.80,其他条件也同样与实验1完全相同,其平均OSPA距离如图7所示。
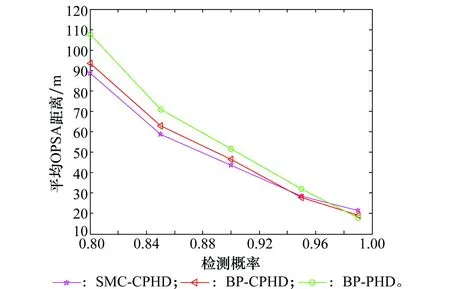
图7 不同检测概率条件下平均OSPA距离Fig.7 Averaged OSPA distance versus detection probability
从图7可以看出,当检测概率为0.99时,3种算法平均OSPA距离相近且都较小,表明检测概率较理想时,三者的估计性能相近,都可以取得较好的估计效果。在检测概率较低的情况下,BP-CPHD和传统的SMC-CPHD群目标跟踪算法的估计性能都优于BP-PHD群目标跟踪算法,而BP-CPHD与传统的SMC-CPHD相比,跟踪性能略有下降,这是由于BP数相对较少,当检测概率较低时,所检测到的BP已经不足以拟合群目标强度函数,而SMC-CPHD所用粒子数较多,仍可较好地近似群目标强度函数。
5 结 论
本文针对群目标跟踪问题,提出一种基于演化网络模型的BP-CPHD滤波算法。算法使用BP-CPHD 进行滤波处理,并通过演化网络模型对群结构进行更新,然后使用所获得的群信息对群内目标的运动状态进行修正,在对每个个体目标状态有效估计的同时,还可以准确地估计群整体的状态。对于群目标跟踪中的一些复杂情况,例如群的分裂、合并等,也能给出较好的估计结果。蒙特卡罗仿真表明,本文所提BP-CPHD群目标跟踪算法在达到与传统的SMC-CPHD群目标跟踪算法相近估计性能的条件下,大幅地降低了算法的运算量,提高了实时性。同时,在强杂波环境下也可获得良好的估计性能。
参考文献:
[1] 李昌玺,周焰,郭戈,等. 弹道导弹群目标跟踪技术综述[J]. 战术导弹技术, 2015, 36(3): 66-73.
LI C X, ZHOU Y, GUO G, et al. Summary of group tracking technology based on ballistic missile[J]. Tactical Missile Technology, 2015, 36(3): 66-73.
[2] 张慧, 徐晖, 王雪莹, 等. 一种基于椭圆随机超曲面模型的高斯混合PHD滤波器[J]. 光学学报, 2013, 33(9): 6-15.
ZHANG H, XU H, WANG X Y, et al. A Gaussian mixture PHD filter for group targets tracking based on ellipse random hypersurface models[J].Acta Optica Sinica,2013,33(9):6-15.
[3] 耿文东, 王元钦, 董正宏. 群目标跟踪[M]. 北京: 国防工业出版社, 2014: 1-25.
GENG W D, WANG Y Q, DONG Z H. Group-targets tracking[M]. Beijing: National Defense Industry Press, 2014: 1-25.
[4] GADALETA S, POORE A B, SLOCUMB B J. Single-frame cluster MFA tracking[C]∥Proc.of the American Control Conference, 2003: 1242-1247.
[5] GADALETA S, POORE A B, ROBERTS S, et al. Multiple hypothesis clustering multiple frame assignment tracking[C]∥Proc.of the Signal and Data Processing of Small Targets, 2004: 294-307.
[6] SUN R, ZHAO L L, SU X H. A novel computationally efficient SMC-PHD filter using particle-measurement partition[C]∥Proc.of the IEEE Symposium on Signal Processing and Information Technology, 2016: 51-56.
[7] DARYASAFAR N, SADEGHZADEH R A, NASER-MOGHADASI M. A technique for multitarget tracking in synthetic aperture radar spotlight imaging mode based on promoted PHD filtering approach[J]. Radio Science, 2017, 52(2): 248-258.
[8] MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Trans.on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.
[9] MAHLER R P S. PHD filters of higher order in target number[J]. IEEE Trans.on Aerospace and Electronic Systems,2007,43(4): 1523-1543.
[10] CLARK D, GODSILL S. Group target tracking with the Gaussian mixture probability hypothesis density filter[C]∥Proc.of the 3rd International Conference on Intelligent Sensors, Sensor Networks and Information, 2007: 149-154.
[11] KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Trans.on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.
[12] 连峰, 韩崇昭, 刘伟峰, 等. 基于SMC-PHDF的部分可分辨的群目标跟踪算法[J]. 自动化学报, 2010, 36(5): 732-741.
LIAN F, HAN C Z, LIU W F, et al. Tracking partly resolvable group targets using SMC-PHDF[J]. Acta Automatica Sinica, 2010, 36(5): 732-741.
[13] GNING A, MIHAYLOVA L, MASKELL S, et al. Group object structure and state estimation with evolving networks and Monte Carlo methods[J]. IEEE Trans.on Signal Processing, 2011, 59(4): 1383-1395.
[14] ABDALLAH F, GNING A, BONNIFAIT P. Box particle filtering for nonlinear state estimation using interval analysis[J]. Automatica, 2008, 44(3): 807-815.
[15] GNING A, RISTIC B, MIHAYLOVA L. Bernoulli particle / box-particle filters for detection and tracking in the presence of triple measurement uncertainty[J]. IEEE Trans.on Signal Processing, 2012, 60(5): 2138-2151.
[16] SCHIKORA M, GNING A, MIHAYLOVA L, et al. Box-particle PHD filter for multi-target tracking[C]∥Proc.of the 15th International Conference on Information Fusion,2012:106-113.
[17] GNING A, RISTIC B, MIHAYLOVA L, et al. Introduction to box particle filtering[J]. IEEE Signal Processing Magazine, 2013, 30(4): 166-171.
[18] 赵雪刚, 宋骊平, 姬红兵. 量化量测条件下的交互多模型箱粒子滤波[J]. 西安电子科技大学学报, 2014,41(6): 37-44.
ZHAO X G, SONG L P, JI H B. Interacting multiple model box particle filter with quantitative measurements[J]. Journal of Xidian University, 2014,41(6): 37-44.
[19] 梁萌. 基于箱粒子滤波的多目标跟踪算法研究[D]. 西安:西安电子科技大学, 2015.
LIANG M. Research on box-particle filter based multi-target tracking[D]. Xi’an:Xidian University, 2015.
[20] SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Trans.on Signal Processing, 2008, 56(8): 3447-3457.
[21] 宋骊平,刘宇航,程轩.箱粒子PHD演化网络群目标跟踪算法[J].控制与决策, 2018, 33(1): 74-80.
SONG L P, LIU Y H, CHENG X. Box-particle evolution network PHD filter for group targets tracking[J]. Control and Decision, 2018, 33(1): 74-80.
