混合车型需求响应公交服务定制问题研究

郑 汉，张星臣，王志美

(北京交通大学 交通运输学院，北京100044)

0 引言

需求响应公交服务(Demand-Responsive Service)，作为一类新兴的城市公共交通组织方式，已成为传统公交方式的有效补充，是当前城市交通实现供需适应的重要手段.

在现有研究中，根据不同服务特性，需求响应公交服务可以分为定制公交、校园巴士、专车服务等不同类型.定制公交[1-2]侧重提供一定频率的、相对固定线路的出行服务；校园巴士[3]侧重于解决“多对一”的定制出行问题；而专车服务[4]主要提供“一对一”的特定出行服务.定制公交一般服务于稳定、足量的客流，而校园巴士、专车服务等主要面对“门到门”服务的需求.

然而，城市出行需求具有复杂多变特性，上述“门到门”服务产品和定制公交产品很难满足所有需求，如瞬时、大规模需求(特大城市内生活区与商业区通勤、球赛散场后的大规模返程)便是难以满足的需求之一.这类出行需求会在局部的时空区域内产生大量的上下车行为，“门到门”服务模式此时会表现得效率低下[3].此外，在技术层面，“门到门”服务定制为典型NP-Hard问题，其求解规模和效率一直受限[5-6]，难以在短时间内生成瞬时、大规模需求的疏散方案.以上说明经典“门到门服务”不能完全满足上述出行需求.为了准时到达预定地点，人们主观上能够接受以牺牲一定程度便利性，换取出行效率的提升——放弃门到门服务，接受指定时空范围内集体出行服务(如拼车服务)已成为可被接受的方式之一.本文将一定客流的乘降地点及时间窗定义为“服务单元”.引入服务单元后，人们需要去特定地点进行乘降，而车辆仅需在服务单元间进行运送.服务可以分解为服务单元的设置和带时间窗的车辆取送，两者的设计需要兼顾乘客方便性，以及车队运输的运营成本.由于需求分布的不均衡性，每个服务单元吸引的乘客数具有差异性.考虑多车型(容量、速度、费用等有所差异)的组织形式，既能满足旅客需求，又能够合理控制成本.综上，本文研究如何基于服务单元，使用有限数量的混合类型车辆完成乘客出行服务的问题，即混合车型需求响应公交服务问题.

本文主要由4节构成.第1节，对服务单元进行数学化描述，并研究出行需求服务单元自动生成技术；第2节，借助Dantzig-Wolfe(D-W)分解，以运输成本最小化为目标，建立有限数量混合类型车辆分配与路径规划的等价分解模型，与一般模型相比，我们增加了最大运行距离、最大运行时间约束；在第3节，以MapReduce为框架，设计基于列生成的分布式算法；第4节，选取了以北京为背景的算例，对比本文提出的分布式列生成算法、集中式列生成算法及商业软件GAMS的结果，对方法的可行性、有效性进行了验证.

1 基于需求分析的服务单元生成方法

网络预约、大数据处理等技术在公交领域已有应用[7-8]，获取乘客预定的乘降地点和时间在技术上已较成熟.服务单元包含分配的乘客、乘降地点和乘降时间窗.如何根据乘客出行需求信息，在候选的地点、时间窗内挑选乘降地点及时间窗，分配乘客构成服务单元，是本节解决的主要问题.

为保障乘客的方便性，模型引入行人最大走形距离dmax，核函数宽度σ等参数；同时为提升计划可行性，引入车辆运行冗余ς.模型涉及符号如表1所示.

表1 服务单元生成模型符号约定Table 1 Notations of service units generation model

服务单元生成过程的目标是最大化各需求到选定服务单元间时空相似度总和.表示为

相似性基于高斯核设计，表示为

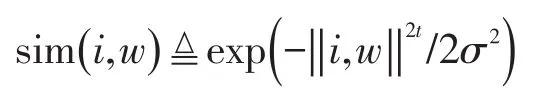
该问题具有以下约束：

(1)服务单元约束.1个簇仅拥有1个服务单元，即∑w∈Sψjw=1，∀j∈C.

(2)预约满足约束.1个预约只能归属于1个簇，即∑i∈Rωij=1，∀j∈C.

(3)候选服务单元内部可行约束.在正常速度下，服务单元的上车点和下车点之间可达，即‖fsti‖Am≥ς，∀i∈Cad.其中‖∙‖Am，∀i∈Cad表示范数，有

(4)最大距离约束.设函数ξ(d is)表示距离和相似度间的映射，有

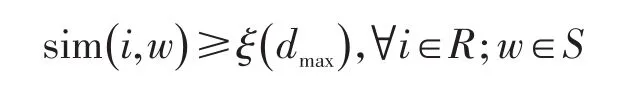
使用基于k-means的启发式算法对模型进行求解，输入为：k(服务单元数)，R(需求集合)，Cad(候选服务单元集合).输出为：k个选定服务单元.具体方法如下：

(1)从Cad中任选k个初始服务单元.

(2)计算所有需求点与候选服务单元的相似度，将需求点分配至各自相似度最大的当前服务单元.在核函数的作用下，若某需求与所有服务单元的相似度均接近0，则该点暂时孤立，并给予目标函数一定惩罚，等待下一次分配.

(3)计算簇内所有需求点的中心，将离中心最近的候选服务单元选为该簇的选定服务单元.

(4)若选定服务单元不再变换，则输出结果；否则，返回步骤(2).

2 车辆分配与路径规划模型

本节内容将解决服务单元和车辆的对应关系问题.该问题被视为带时间窗约束的车辆取送问题，一般方法(文献[5])仅能实现小型案例[6].为解决上述问题，使用Dantzig-Wolfe(D-W)分解，将问题分为主问题与子问题模型.主问题解决服务单元集合的覆盖问题，子问题解决不同类型车辆的路径规划问题，两者可通过边际成本和递减成本关联，使用列生成算法进行求解.混合车型在主问题和子问题中均有体现：主问题中发车的固定费用，子问题中车辆的最大行驶距离、最大行驶时间及载运能力，均由车辆类型决定.

2.1 载运车辆分配主问题模型LMP

主问题模型LMP的符号约定如表2所示.

表2 主问题符号约定Table 2 Notations ofLMP

基于此符号约定，构建LMP模型为

目标函数：

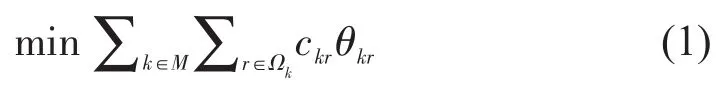
约束条件：

式(2)保障服务单元被分配至1个路径之中；式(3)保障k车的路径r至多被选择1次；式(4)表示决策变量θkr松弛为0-1变量.为提升求解速度，对决策变量θkr进行线性松弛，将式(4)改为θkr∈[0 , 1]，r∈Ωk,k∈M；同时将式(2)改为i∈N.新约束式(2)表示任意服务单元需要被服务但服务次数不受限制.显然，当约束中的“＞”号成立时，问题未达最优解[6].

2.2 路径规划与评价子问题模型Sk

子问题模型的符号定义如表3所示.

表3 子问题符号定义Table 3 Notations ofSk

目标函数：

约束条件：

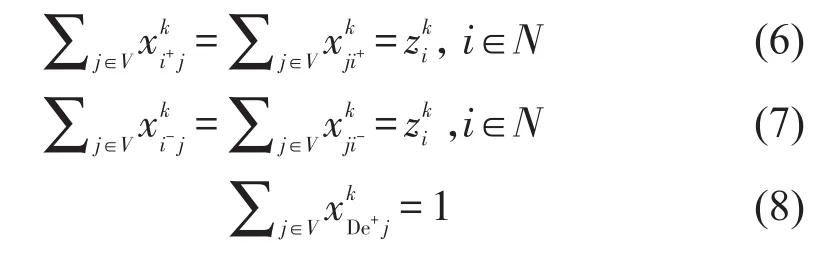
式(6)和式(7)限定载运车辆必须经过服务单元的上、下车部分.式(8)和式(9)限定载运车辆起终点在车队驻扎点.式(10)～式(12)和式(18)组成优先级约束.式(13)～式(15)和式(19)组成能力约束.式(16)和式(17)限定载运车辆运行过程中的最大距离和最大时间.

3 分布式列生成求解算法

3.1 MapReduce框架下的列生成算法

为了实现多节点分布式计算，一方面，使用Hadoop分布式文件系统(简称HDFS)解决节点数据高效率读、写问题；另一方面，通过MapReduce框架解决分布式算法的协调组织与同步推进问题.图1通过一个4节点系统描述了MapReduce框架下的列生成算法的基本情况.节点1～3侧重子问题的求解，节点0侧重主问题的求解.算法描述如下.

Step 1初始化.将服务单元信息、车队信息，以及初始化路径集(路径和费用)输入HDFS之中.其中，初始化路径集的构建需要引入虚拟变量及虚拟路径.虚拟路径定义为目标函数为一极大正值，且θkr=0的路径[5-6]；虚拟变量表示虚拟路径是否被使用，初始化时虚拟变量均为1.

Step 2规约.MapReduce从HDFS中获取所有路径集Ωk，并运行Reduce函数，通过线性规划方法求解LMP，获得当前最优解，计算LMP的边际成本

Step 3判断.对当前最优解进行终止判断，包括：

①若虚拟变量取0，且子问题的目标函数值大于等于0时，则停止计算并输出；

②若虚拟变量不取0，且子问题的目标函数值大于等于0时，则停止计算并告知无解；

③若子问题的目标函数值小于0，则继续计算；

④若子问题尚未计算，则继续计算.

Step 4存储.将LMP获得的解、边际成本( )u→,v→及新的路径集Ωk存入HDFS.

Step 5读取.MapReduce从HDFS中获取服务单元信息，车队信息，以及当前主问题的边际成本

Step 6映射.根据车辆类型对参数进行映射，构建不同分片发送至节点1～3，存储于Datanode并交由Tasktracker调度.之后在Map函数中求解对应的子问题Sk.Sk可以被视为从De+到De-的具有优先级约束、能力约束和资源约束的最短路问题，可使用文献[9]中算法求解.将各子问题求解由Jobtracker控制.

Step 7结合.选择子问题解中的最优解，按照类型添加进路径集Ωk，并存入HDFS，之后返回Step2.

3.2 MapReduce框架下的解可行性保障方法

主问题的松弛可以提升求解效率，同时也可能造成解中出现路径由非整数辆车执行的情况.为保障解的可行性，制定如下策略.

Step 8选边.选取满足的边，构建禁忌路径集TR1⊆Ωk及TR2⊆Ωk和禁忌边集TA1⊆A和TA2⊆A.其中TR1是包含边a的所有路径集合，而TR2是TR1的补集；TA1包含边a，而TA2包含与边a拥有相同指向点的边.

Step 9分支.根据下述方法进行分支：

①分支1，根据TR1，排除Ωk中的路径.并根据TA1，删除A中的相关信息.

②分支2，根据TR2，排除Ωk中的路径.并根据TA2，删除A中的相关信息.

Step 10重初始化.将分支后数据写入HDFS，并返回Step2进行运算.

完成计算后，比对各分支的结果，选择可行且最优的解作最终解.

图1 MapReduce框架Fig.1 Framework based on MapReduce

4 实例运用与结果分析

本文通过模拟预约系统共获得357个预约需求，时区为6:00-12:00，分布于北京市昌平区和海淀区.

以100 m为间隔，调整服务单元生成模型中的参数dmax进行数值实验，发现该案例中，当dmax在100～800 m范围时，总是存在孤立点.为此，在接下来的试验中，我们采取dmax=900 m进行研究(尽可能减少步行距离).此时可获得25个服务单元.初步分析可知，在6:00-9:00，服务单元的上车点集中在西二旗、回龙观等住宅区，以及西直门等枢纽，下车地点集中在科技、教育与商业中心，客流由城外向城内流动(图2(a))；在9:00-12:00的服务单元，其上车点与下车点分布在海淀区的学校、商场、办公区等区域(图2(b)).大体上符合北京市的基本情况.服务单元所组成的网络模型如图3所示，其中车队驻扎地以“Depot”表示，标号0；所有上车地点以“+”表示，编号为1～25；而下车地点以“-”表示，编号26～50.

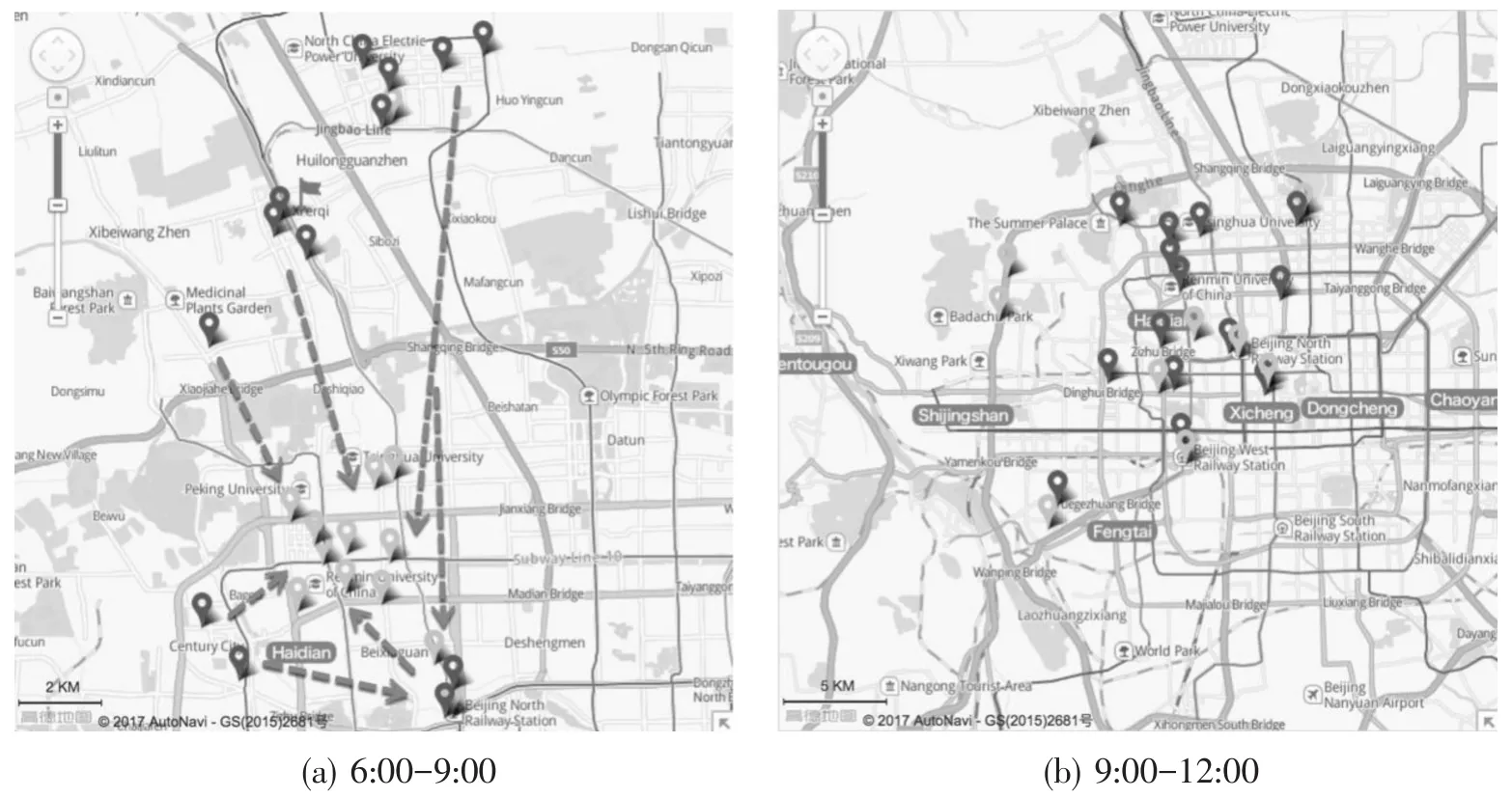
图2 服务单元分布情况Fig.2 Distributions of service units

图3 服务单元网络模型图Fig.3 Network model for service units

设定车队1规模：22座小车(车型1)3辆和53座大车(车型2)9辆，共计12辆.车辆固定费用设置为45(车型1)和90(车型2)，而活动成本由行驶距离表示.车辆行驶细节由数字地图提供.

本文设计了5组试验，如表4所示，使用的计算资源为Intel(R)Core(TM)i7-6500U CPU@2.50GHz 2.59GHz，内存 4.00GB，节点数 3，宽带100 MB/s.其中算例1以改进的经典模型[5]建模(添加约束式(16)和式(17))，使用商业软件GAMS求解，作为解质量的标准；算例2使用非分布式的列生成算法[6]对第2节模型进行求解，作为计算速度的标准；算例3采用本文第2节的模型和第3节的算法.前3组均以车队1为研究基础.

对比分析，算例1～3解的目标值相同，证明第2节模型与原模型等价，方法可行.从计算时间来看，解1消耗了71 835 ms，解2消耗了36 786 ms，而解3消耗了16 184 ms，由此证明分布式列生成算法在计算时间上有足够的优势.

此外，我们设计了算例4和算例5，分别表示单纯使用车型1和车型2时的计划情况.算例3总共使用了10辆车，包括2辆车型1和8辆车型2，满载率76%.算例4由于能力不足导致无解.算例5目标函数为1 545.275，使用10辆车型2，满载率67%.由此可见，同样的需求下，混合车型的供需匹配更为合理.算例3的解如表5所示.

表4 不同数值实验解质量对比Table 4 Quality comparison among solutions

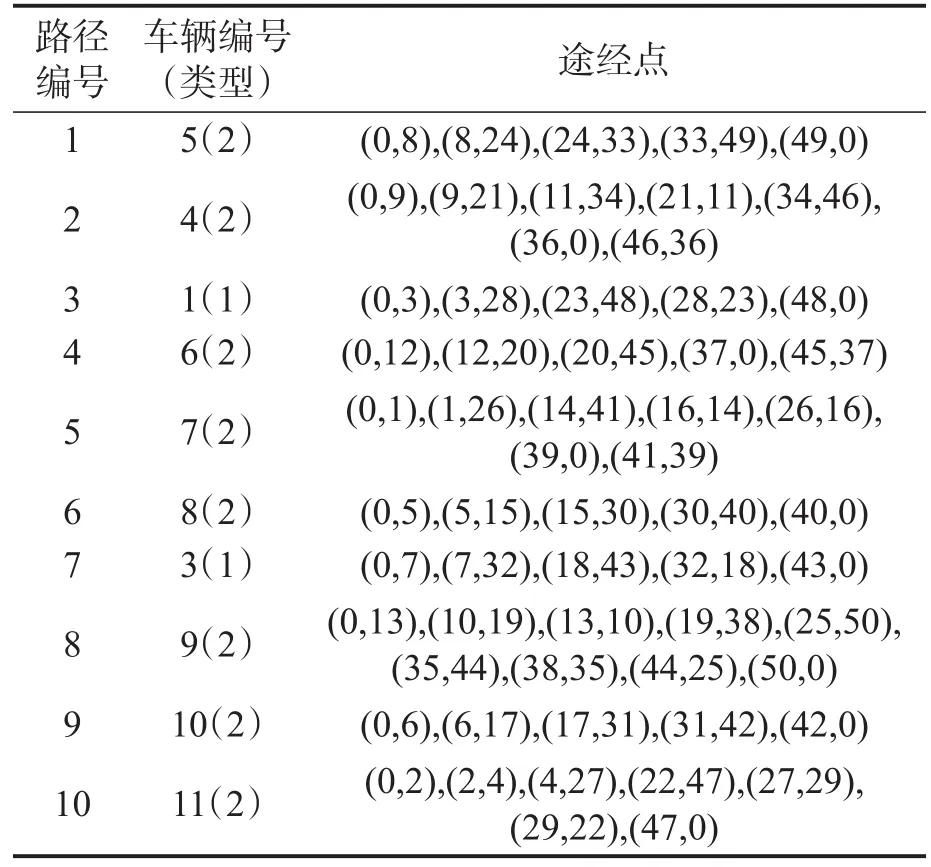
表5 解3的路径详情Table 5 Details of routes in solution 3

5 结论

本文通过设计算法分析需求，确定服务单元.将载运车辆的分配与路径规划问题视为带时间窗的取送问题，通过D-W分解建立等价分解模型，提出分布式列生成算法和解的可行性保障方法.实例证明，提出的分解模型与原问题等价，设计的算法相较于集中式算法在效率上有一定的优势.混合车型需求响应公交服务具有一定的实际应用价值.

参考文献：

[1]LIU T,CEDER A,BOLOGNA R,et al.Commuting by customized bus:A comparative analysis with private car and conventional public transport in two cities[J].Journal of Public Transportation,2016,19(2):55-74.

[2]PERUGIA A,MOCCIA L,CORDEAU J F,et al.Designing a home-to-work bus service in a metropolitan area[J].Transportation Research Part B Methodological,2011,45(10):1710-1726.

[3]PARK J,KIM B I.The school bus routing problem:A review[J].European Journal of Operational Research,2010,202(2):311-319.

[4]RITZINGER U,PUCHINGER J,HARTL R F.Dynamic programming based metaheuristics for the dial-a-ride problem[J].Annals of Operations Research,2016,236(2):341-358.

[5]SOL M.Column generation techniques for pickup and delivery problems[D]. Technische Universiteit Eindhoven,1994.

[6]FEILLET D.A tutorial on column generation and branch-and-price for vehicle routing problems[J].4OR,2010,8(4):407-424.

[7]REN Y,CHEN G,HAN Y,et al.Extracting potential bus lines of customized city bus service based on public transport big data[J].Iop Conference Series:Earth&Environmental Science,2016,46(1):012017.

[8]LEI Y W,LIN P Q,YAO K B.The network scheduling model and its solution algorithm of internet customized shuttle bus[J].JournalofTransportation Systems Engineering and Information Technology,2017,17(1):157-163.

[9]DUMAS Y,DESROSIERS J,SOUMIS F.The pickup and delivery problem with time windows[J].European Journal of Operational Research,1991,54(1):7-22.