轨道交通槽形梁结构振动与噪声特性研究

秦佳良，刘林芽，宋瑞，曾峰

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

随着经济的飞速发展和城市人口密度的增大，城市轨道交通将成为城市交通的主要形式。轨道交通槽形梁更是因其建设周期较短、费用较低、美观性能较好等优点，已经广泛运用于城市轨道交通当中。但随之而来的振动与噪声问题却比较严重，成为了制约其发展的重要因素，因此对轨道交通槽形梁的振动噪声研究就显得很有必要。目前，国内外学者研究箱形梁结构振动与噪声的问题较多[1−3]，但对槽形梁的声振特性研究还比较少，而且关于边界条件对槽形梁振动与噪声的影响的研究更是罕见。吴亮秦等[4]运用车桥耦合振动理论分析了城市轨道交通高架桥U型梁的位移动力系数、总体应力动力系数和道床板局部应力动力系数，主要从动力系数的角度考察槽形梁的动力特性，但没有对槽形梁结构噪声进行分析。李奇等[5]采用有限元法和模态叠加法求解列车−轨道−桥梁动力相互作用系统瞬态响应，重点关注桥梁高频局部振动, 再采用边界元法求解桥梁模态声传递向量，将其与桥梁模态坐标频谱相乘得到空间各场点声压频谱，主要分析了槽形梁结构噪声辐射特性，但对槽形梁结构振动特性研究的还比较少。罗文俊等[6]基于车辆−轨道耦合动力学原理，利用有限元法分析了边界条件对箱形梁的局部振动特性的影响，但都没有分析边界条件对桥梁结构噪声的影响。本文以30 m的轨道交通槽形梁为研究对象，基于车辆−轨道耦合动力学理论[7−8]，采用有限元−间接边界元耦合分析方法，计算并分析列车荷载作用下槽形梁的声振特性，而后研究有限元模型的边界条件对桥梁结构的自振频率的影响，并对比分析不同边界条件对槽形梁结构振动与噪声的影响，为轨道交通槽形梁的减振降噪提供参考。

1 槽形梁振动与噪声的计算模型

1.1 槽形梁有限元模型建立

某轨道交通线槽形梁[9]标准跨径为30 m，其道床板宽度为3.634 m，底板厚0.24 m，距梁端1.2 m范围内道床板局部加厚为0.32 m，如图1所示。该梁为全预应力结构，混凝土强度等级C50，承轨台和桥面板整体浇注。

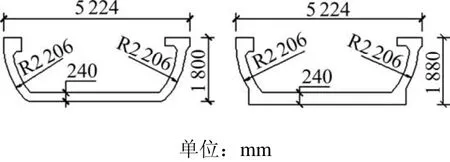
图1 槽形梁截面尺寸Fig. 1 Trough beam section size

在有限元模型当中，钢轨采用梁单元beam188

来模拟，扣件采用弹簧单元combine14单元模拟，承轨台采用实体单元solid185单元模拟；由于板壳单元能很好的显示桥梁的整体及局部的振动特性，因此利用赋予实际厚度的板壳单元shell181单元来模拟桥梁。因为承轨台和桥面板是整体浇注的，所以建模时通过节点耦合的方法使槽形梁和承轨台固结在一起，有限元模型见图2所示。

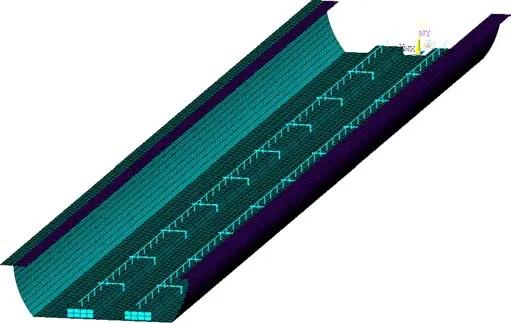
图2 槽形梁有限元模型Fig. 2 Finite element model of trough beam

测试[5]表明梁−墩−基础体系基频为2.25 Hz，对应的振型为墩体横弯。且桥近场梁结构噪声主要受单孔槽形梁局部振动而非梁−墩−基础体系整体振动影响，所以不考虑桥墩及附属结构的影响。因此，本文只建立单孔槽形梁的有限元模型，并简支约束于桥墩4个支座位置。

1.2 车辆−轨道耦合振动模型

采用文献[10]中的车辆−轨道耦合系统，建立板式无砟轨道垂向耦合双层梁模型，利用 Newmark积分方法求解车辆－轨道耦合振动模型的动力微分方程，得出轮轨相互作用力。

采用 2节地铁 A型车模拟加载，计算速度取80 km/h。采用文献[9]中提供的轨道不平顺谱模拟得到不平顺样本，考虑轨道不平顺谱波长范围为0.1~25 m，得到图3所示的高低不平顺样本。由此计算出的不平顺激励频率为0.89~222.2 Hz，这可满足槽形梁整体、局部振动及结构噪声的分析要求。

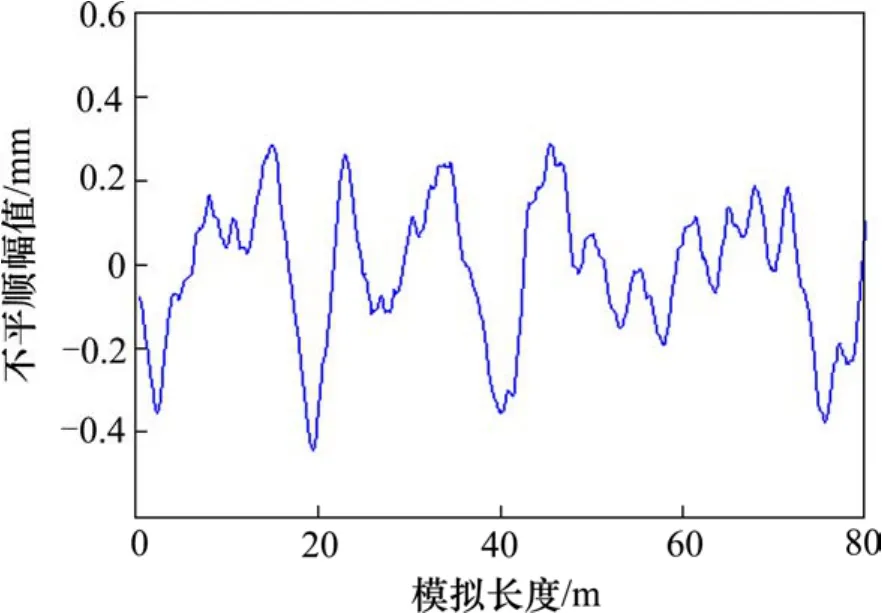
图3 高低不平顺样本Fig. 3 Sample of vertical irregularities

将列车实际运行过程简化为一系列随时间移动的集中力荷载，将这些移动的集中力荷载加载到槽形梁的有限元模型上[12−13]计算槽形梁的振动响应，加载的时间步长取为0.001 8 s。

1.3 轨道交通槽形梁边界元模型

边界元法相对于有限元法降低了求解问题的计算维度，并且在边界自动满足远场辐射条件。对于轨道交通槽形梁，计算结构振动辐射噪声时建立的边界元模型的边界网格不封闭，在计算时需采用间接边界元方法求解边界积分方程。间接边界元法可以由直接边界元法推导得到[11]。与直接边界元不同，间接边界元方法引入了位势的概念，计算的声场是在边界元网格的两边，需要确定边界元两侧的声压差和声压梯度的差。

根据流体介质的守恒原理和关于声波动的一些基本假设，可知Helmholtz方程表达式如下：

式中：/kcω=；p为声压；k为波数；ω为角频率；c为介质中的声速。

由于在声场和固体结构耦合边界上，重合的点具有相同的边界条件，因此知道了固体边界上的位移响应结果，就可以计算声场边界上的声压，进而求得整个声场中任意一点的声压。

在计算结构噪声时，必须考虑各种因素对声辐射的影响。反射面的反射对声场的分布影响非常显著[11]。为简化分析，在声学计算过程当中，把地面当做全反射面进行分析。

在建立声学边界元模型时，通常假设在最小波长内有6个单元，也就是最大单元的边长要小于计算频率最短波长的 1/6，或者要小于最高计算频率点处的波长的 1/6，即最大单元的边长要满足如下表达式

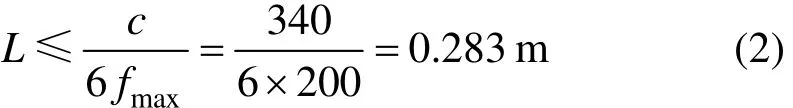
槽形梁的边界元模型及场点网格如图3所示。

图4 槽型梁边界元模型及场点网格Fig. 4 Trough beam boundary element model and mesh point

2 槽形梁振动特性分析研究

在对槽形梁振动分析中，本文采用瞬态动力学分析桥梁的动力响应，得到在随时间变化的荷载作用下结构节点位移、应力、速度、加速度等的响应。瞬态动力学分析也称为时间历程分析，其基本运动方程为：

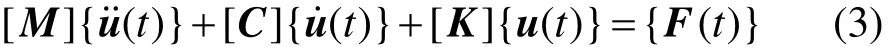
式中：[M]，[C]和[K]分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；{()}tu˙˙ ，{()}tu˙ 和{u(t)}分别为系统节点的加速度、速度和位移向量；{F(t)}为系统的节点荷载向量。

本文为研究轨道交通槽形梁结构的振动特性，选取如图5中所示的槽形梁跨中截面的输出点，其中1~3号输出点分别表示槽形梁跨中处底板线路中心位置和左右腹板的中心位置。通过有限元瞬态分析，可以得出输出点的时域响应，再通过傅里叶变换进行频谱分析，得到如图6~7所示的输出点的加速度振级频谱曲线。

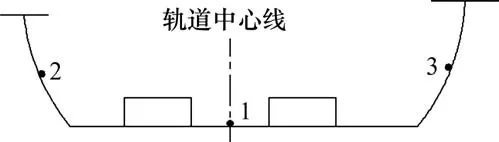
图5 槽型梁跨中截面振动响应输出点Fig. 5 Vibration response output point in midspan of trough beam

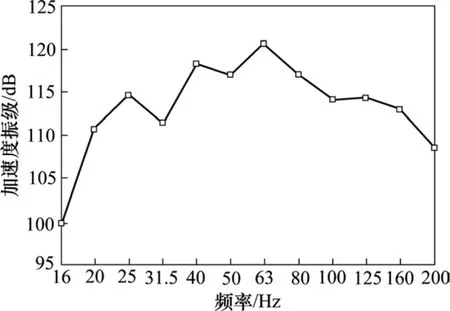
图6 底板垂向加速度振级频谱图Fig. 6 Vertical acceleration spectrum curve of the bottom deck

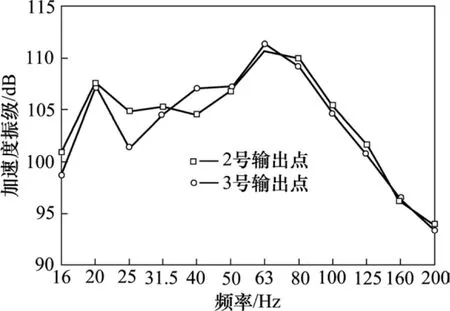
图7 腹板横向加速度振级频谱图Fig. 7 Transverse acceleration spectrum curve of web

由图6和图7可知，槽形梁底板的垂向振动加速度振级的峰值频率和腹板横向振动加速度振级的峰值频率相等，且都为63 Hz。而且槽形梁底板的垂向振动响应最大，其最大的垂向加速度振级为120.6 dB。这可能是因为槽形梁底板是直接承受列车动荷载作用的构件，所以底板的垂向振动响应是最大的。而且槽形梁的腹板相当于一个悬臂结构，底板的垂向振动会引起腹板的横向振动，所以它们的峰值频率会相同。

3 槽形梁声辐射特性分析研究

将计算得到的槽形梁结构的振动响应作为声学边界元的初始条件，导入到声学软件 virtual.lab中求解各个场点的声压响应。为研究距槽形梁线路中心线水平向不同距离处的声场分布规律，选取槽形梁跨中6个场点进行分析，如图8中所示。因为桥梁结构噪声以低频为主，而现行的A计权评价指标对低频噪声有大幅度的衰减，所以为准确评价槽形梁的结构噪声，本文采用无计权的线性声压级进行分析。图9所示为6个场点线性声压级的1/3倍频程曲线。

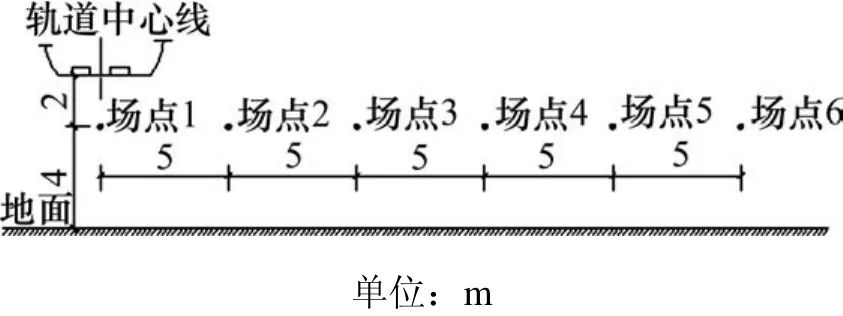
图8 槽形梁跨中场点分布图Fig. 8 Sound point distribution in middle span of trough beam

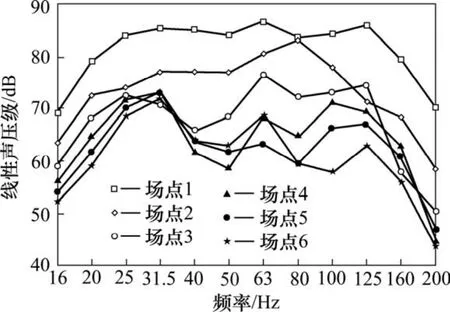
图9 场点声压级频谱图Fig. 9 Transverse acceleration spectrum curve of web

由图9分析可知，随着离桥梁的距离越远，场点的最大声压级也越小，而且槽形梁结构噪声的峰值频率在31.5~80 Hz之间。由图9可知，槽形梁结构噪声的峰值频率在63 Hz附近，这与文献[9]中的峰值频率吻合得很好。这有可能是因为槽形梁结构振动的峰值频率也在63 Hz。而且，通过考察槽形梁结构的模态特征，发现频率在63 Hz附近的振动模态比较密集，若列车的激振频率在此范围内较大时，容易引起结构的共振。

4 边界条件的影响分析

下面将对比在简支与固支两种边界条件下，槽形梁结构振动与噪声的不同。本文中所说的固支边界是指在桥梁两端面上的所有节点的6个自由度均约束。表1列出了两种边界条件下的前5阶自振频率，当槽形梁为固支边界时，其受到的约束更强，自振频率也相应增加。

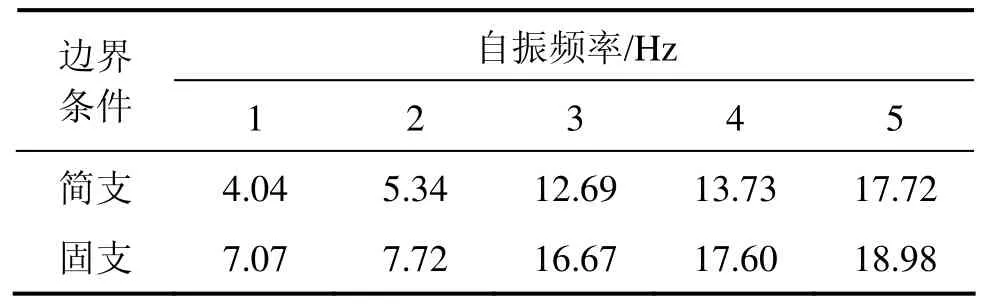
表1 槽形梁前5阶动力特性Table 1 Natural frequency of the first 5 orders of the trough beam

表2列出了各个输出点的最大加速度振级和各个场点的最大线性声压级，可以看出，简支梁产生的噪声比固支梁大，如果采用固支梁，降噪效果特别可观，可减少大约6 db。主要原因是固支梁受到的约束更强，在列车荷载作用下的振动响应比简支梁要小很多，所以桥梁辐射的结构噪声比简支梁要小。在工程实际中，完全固支的边界条件难以实现，但可以采用将多跨的简支梁变为连续梁的方法，来降低桥梁结构的振动和噪声。

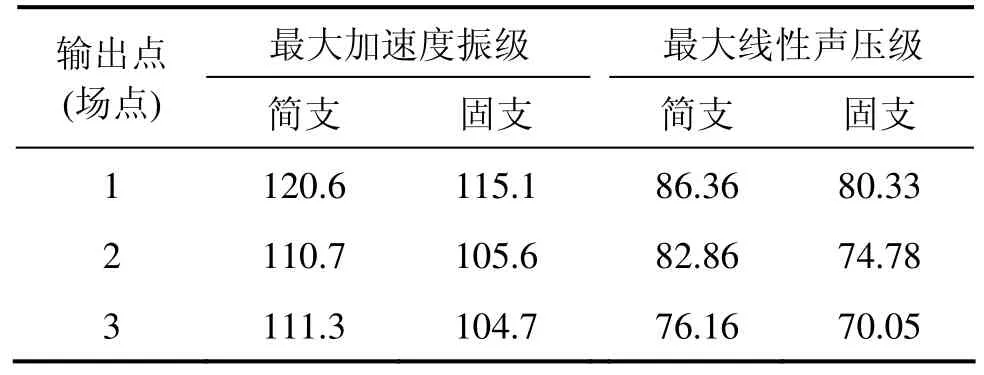
表2 边界条件对桥梁结构振动与噪声的影响Table 2 Influence of boundary conditions on vibration and noise of bridge structures

5 结论

1) 槽形梁底板的垂向振动加速度和腹板的横向振动加速度的峰值频率都为63 Hz。

2) 离桥梁的距离越远，场点的最大声压级越小。

3) 槽形梁结构噪声的线性声压级峰值频率在31.5~80 Hz之间。

4) 采用固支边界会使桥梁结构自振频率变大，并可以降低桥梁结构的振动与噪声。

参考文献：

[1] 高飞, 夏禾, 曹艳梅, 等. 城市轨道交通高架结构振动与声辐射研究[J]. 振动与冲击, 2012, 31(4): 72−76.GAO Fei, XIA He, CAO Yanmei, et al. Vibration and noise influences of elevated structures in urban railway[J].Journal of Vibration and Shock, 2012, 31(4): 72−76.

[2] Ngai K W, Ng C F. Structure-noise and vibration of concrete box structure and rail viaduct[J]. Journal of Sound and Vibration, 2002, 255(2): 281−297.

[3] Ouelaa Nourdine, Rezaiguia Abdelouahab, Laulagnet Bernard. Vibro-acoustic modelling of a railway bridge crossed by a train[J]. Applied Acoustics, 2006, 67(5):461−475.

[4] 吴亮秦, 吴定俊, 李奇. 城市轨道交通U型梁车桥动力响应分析[J]. 铁道科学与工程学报, 2010, 7(6): 6−11.WU Liangqin, WU Dingjun, LI Qi. Vehicle-bridge dynamic response analysis of U-girder for urban rail transit[J]. Journal of Railway Science and Engineering,2010, 7(6): 6−11.

[5] 李奇, 吴定俊. 混凝土桥梁低频结构噪声数值模拟与现场实测[J]. 铁道学报, 2013, 35(3): 89−94.LI Qi, WU Dingjun. Numerical simulation and field tests of concrete bridge-borne low-frequency noise[J]. Journal of the China Railway Society, 2013, 35(3): 89−94.

[6] 罗文俊, 张辛元. 高速铁路高架桥局部振动的有限元分析[J]. 噪声与振动控制, 2014, 34(6): 148−152.LUO Wenjun, ZHANG Xinyuan. Analysis of local vibration for high-speed railway bridge by means of finite element method[J]. Noise and Vibration Control, 2014,34(6): 148−152.

[7] 雷晓燕. 高速铁路轨道动力学—模型、算法与应用[M].北京: 科学出版社, 2015: 85−94.LEI Xiaoyan. High speed railway track dynamics: model,algorithm and application[M]. Beijing: Science Press,2015: 85−94.

[8] 翟婉明. 车辆—轨道耦合动力学[M]. 3 版. 北京: 科学出版社, 2007: 83−84.ZHAI Wanming. Vehicle-track coupling dynamics[M].3rd ed. Beijing: Science Press, 2007: 83−84.

[9] 韩江龙, 吴定俊, 李奇. 城市轨道交通槽型梁结构噪声计算与分析[J]. 工程力学, 2013, 30(2): 190−195, 202.HAN Jianglong, WU Dingjun, LI Qi. Calculation and analysis of structure-borne noise from urban rail transit trough girders[J]. Engineering Mechanics, 2013, 30(2):190−195, 202.

[10] 刘林芽, 吕锐, 刘海龙. 无砟轨道垂向高频振动响应分析[J]. 铁道科学与工程学报, 2011, 8(6): 1−6.LIU Linya, LU Rui, LIU Hailong. Vetical high frequency vibration response analysis of ballastless track[J]. Journal of Railway Science and Engineering, 2011, 8(6): 1−6.

[11] 李克冰, 张楠, 夏禾, 等. 高速铁路 32 m 简支槽形梁桥结构噪声分析[J]. 中国铁道科学, 2015, 36(4): 52−59.LI Kebing, ZHANG Nan, XIA He, et al. Analysis on structure-borne noise of 32 m simply-supported trough girder bridge for high speed railway[J]. China Railway Science, 2015, 36(4): 52−59.

[12] CHEN Y J, JU S H, NI S H, et al. Prediction methodology for ground vibration induced by passing trains on bridge structures[J]. Journal of Sound and Vibration, 2007, 302: 806−820.

[13] 高传伟, 唐雅茹, 余华. 基于移动荷载过桥的轨道交通桥梁振动研究[J]. 中国铁道科学, 2005, 26(2): 73−76.GAO Chuanwei, TANG Yaru, YU Hua. Study on the vibration of rail transit bridge based on moving load passing bridge[J]. China Railway Science, 2005, 26(2):73−76.