岩体相似材料正交设计试验研究

姚国强 ，言志信

(1. 安徽理工大学 土木建筑学院，安徽 淮南 232000；2. 河南城建学院 土木与交通工程学院，河南 平顶山 467000)

相似模型试验广泛应用于高陡边坡、采矿工程、地下工程等复杂地质工程的研究，通过模型试验表现出的力学特性和变形特征，可为实际工程提供更加科学的理论依据。另外，相较于数值模拟分析，模型试验能够分析结构从弹性到塑性，直到破坏的全过程，是一种更加直观、更具说服力的研究方法。根据相似理论，通过配制相似材料进行模型试验中，相似材料的选择及配比对模型试验结果起着决定性作用[1]。因此，研制出符合原型与模型物理力学参数相似比的岩体相似材料至关重要。目前，关于岩体相似材料的研究，前人已做了大量的工作，取得了一定的成果[2−7]。张强勇等[8]以重晶石粉、铁精粉、石英砂为骨料，松香、酒精溶液为胶结剂，石膏为调节剂，研制一种新型铁精砂相似材料(IBSCM)，可用来模拟大部分岩体材料；韩伯鲤等[9]采用铁粉、红丹粉、重晶石粉、氯丁胶浆和松香酒精溶液研制出一种新型地质力学模型材料(MIB)，该种材料的各种成分胶结成型后不发生化学反应，研碎后可以重复利用；李树忱等[10]以砂、滑石粉和石蜡为原料研制出一种非亲水性的新型固流耦合相似材料，该材料可较好地模拟不同渗透性的中低强度的岩体。马芳平等[11]采用磁铁矿精矿粉、河沙、石膏或水泥、拌和用水及添加剂成功研制出NIOS地质力学模型材料，该种模型材料重度较大并且弹性模量和抗压强度具有较大的调节范围。但是，目前研制的岩体相似材料大都只适用于夯压[12−13]或砌筑[14−15]的试验模型。然而，夯压方式下，模型存在局部受力不均的问题；而砌筑方式下，模型存在过多的纵横结构面，故使用夯压或砌筑方式均无法较好地模拟制作岩质试验模型。另外，目前针对以直接浇筑方式制作试验模型的岩体相似材料研究鲜有报道。试验表明，采用浇筑方式制作的试验模型，其各部分材质均匀，能够更好地模拟实际中的岩体工程。此外，直接浇筑使模型制作得到简化，且节约时间，从而使得模型试验变得更加高效。因此，对于能够直接浇筑的岩体相似材料进行试验研究非常必要。本文应用正交试验设计方法进行岩体相似材料配比研究，采用直接浇筑的方式制备试验试样。对正交试验结果进行线性回归分析和方差分析，量化了相似材料物理力学参数与影响因素之间的关系，并且得出了各因素对参数影响的显著性。研究成果对研制以浇筑方式制作试验模型的岩体相似材料具有重要的参考价值。

1 试验过程

1.1 相似材料选择

相似材料选择的正确与否，将直接影响模型试验的结果。通过分析总结前人对相似材料的研究成果以及考虑模型制作的方式，并本着材料价廉易得、制作工艺简单、无毒无害及改变材料配比可使材料的物理力学参数指标具有较大调节范围等原则[8]。本文以重晶石粉、铁精粉和石英砂为骨料，石膏和水泥为胶结剂以及甘油作为调节剂进行岩体相似材料配比研究。其中，石膏选用模型石膏，水泥为C42.5的基准水泥，甘油的纯度为95%。重晶石粉细度规格为400目，密度约为4.2 g/cm3，铁精粉细度规格为60~100目，密度约为5.12 g/cm3，石英砂细度规格为20~35目，密度约为2.73 g/cm3，3种骨料的密度较大、物理化学性质稳定且级配良好,是制作模型试验的理想材料。

1.2 正交试验方案设计

正交试验设计是研究多因素、多水平的一种设计方法，它是根据正交性从全面试验中挑选出部分有代表性的水平组合进行试验，这些有代表性的水平组合具备了均匀分散和齐整可比的特点。正交试验设计采用正交表进行统筹安排试验，正交表具有均衡性、正交性和代表性，从而可使得进行较少的试验次数，而获得具有较强代表性的数据，进而使得从部分试验结果中可了解全面试验的情况，使得试验更加高效、经济[16]。

在本次试验中，选取A因素为(重晶石粉+铁精粉)/骨料、B因素为铁精粉/(铁精粉+重晶石粉)、C因素为胶结剂含量(占固体总量)、D因素为石膏/胶结剂及E因素为甘油含量(占固体总量)作为正交试验设计的5个因素，每个因素均匀设置4个水平，如表1所示。选用5因素4水平正交表L16(45)，共16组试验，材料配比方案如表2所示。

表1 相似材料正交设计水平Table 1 Orthogonal design level of similar material

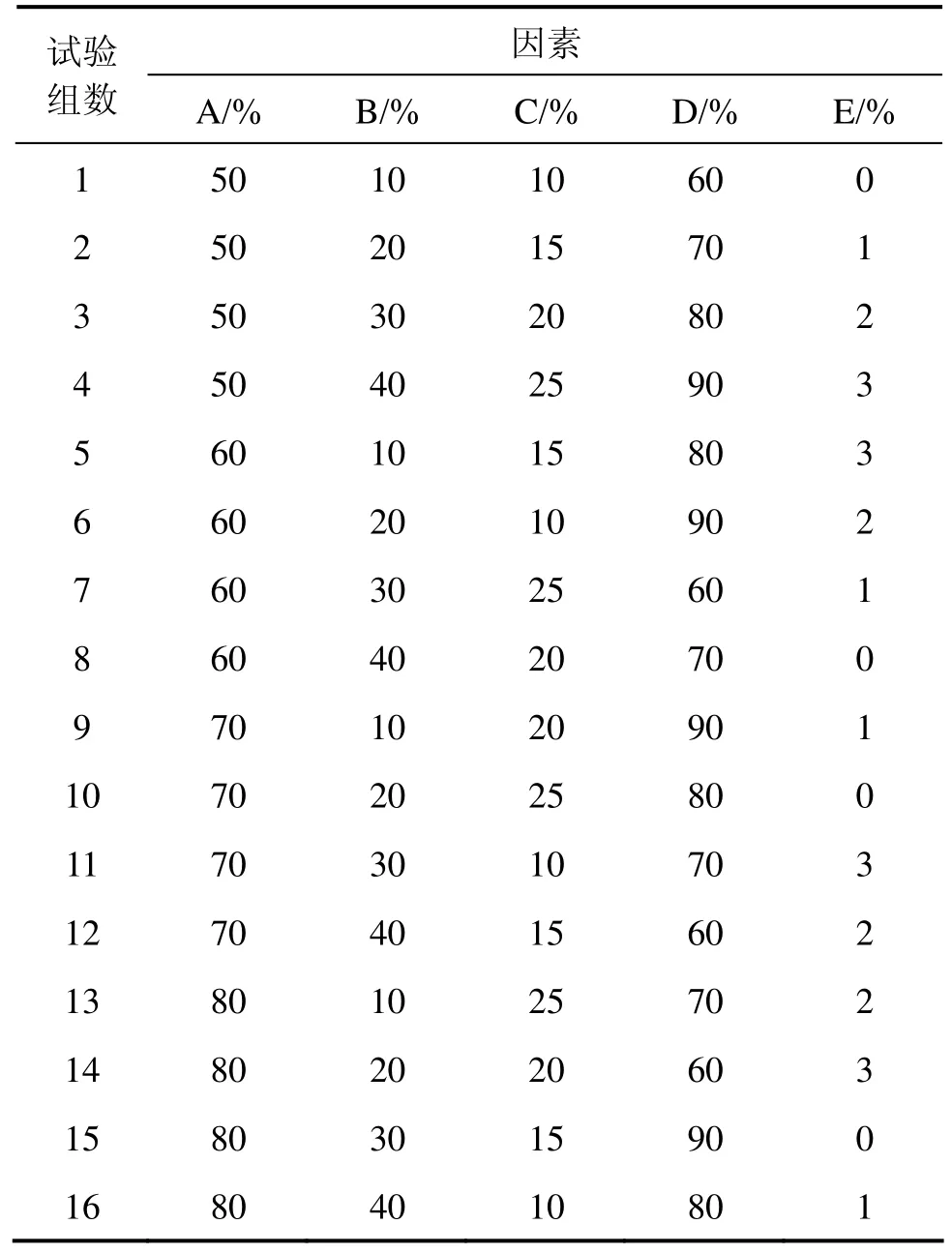
表2 相似材料配比方案Table 2 Test schemes of similar material

1.3 相似材料试样制作

试样制作时，首先，将称量好的石英砂、铁精粉、重晶石粉、水泥、石膏依次加入到搅拌机里，待混合料搅拌均匀后，再加入溶解甘油的适量水，另外，为了提高混合料的流动性，以方便后期模型浇筑制作，在每份材料(600 g)中加入2.5 g聚羧酸型减水剂；然后，将拌和好的混合料浇注进模具中，并振捣密实；最后，在室温25 ℃条件下，养护2 h后脱模，并将试样进行编号标记，放置在室内自然养护7 d后进行试验。

本次试验是在进行了大量试配的前提下，大致确定了各种成分混合料试样的物理力学参数范围的条件下进行的，为进一步优化所需参数，制备了16组不同配比的相似材料试样，每组的3种试样即单轴压缩试样、直剪试样和劈裂试样，各制作4个，共制作192个试样，如图1所示。

图1 试验试样Fig. 1 Test sample

1.4 试样参数测试

为了确定相似材料的密度(ρ)，抗压强度(σc)，抗拉强度(σt)，弹性模量(E)，泊松比(μ)，黏聚力(c)和内摩擦角(φ)等物理力学参数, 分别对试样进行了称量、单轴压缩试验、劈裂试验和直剪试验。单轴压缩试验的试件尺寸为Φ50 mm×100 mm的圆柱体，劈裂试验的试件尺寸为Φ50 mm×50 mm的圆柱体，直剪试验的试件尺寸为 70.7 mm×70.7 mm×70.7mm的正方体，力学参数测试均在 TAW-2000微机控制岩石三轴试验系统上进行，如图2所示。相似材料正交试验结果如表3所示。

图2 微机控制岩石三轴试验系统Fig. 2 Microcomputer controlled rock triaxial test system

表3 相似材料正交试验结果Table 3 Orthogonal test results of similar material

2 试验结果分析

2.1 相似材料参数分析

由表3相似材料正交试验结果可知，相似材料的密度分布在2.45~2.87 g/cm3，表明该相似材料具有较高的重度，可以较好地满足重度相似比的Cγ=1的岩体材料，进而可简化模型与原型之间相似比的换算，使模型制作得到简化。抗压强度分布在3.73~20.38 MPa，抗拉强度分布在0.379~2.324 MPa，弹性模量分布在423.34~2 968.83 MPa，泊松比分布在0.175~0.254，黏聚力分布在 1.023~3.738 MPa，内摩擦角分布在24.89°~43.71°，表明该相似材料的力学参数具有较大的可调范围，能够满足大部分岩体模型试验对相似材料的要求。根据表中相似材料正交试验结果可选择符合模型试验要求的配比材料或可缩小相似材料的配比范围，从而使得确定合适相似材料配比的工作量大大减少，以利于后期模型试验。

2.2 参数与各因素之间的定量关系

相似材料的物理力学参数同时受到多个因素的共同影响，每一个因素的变化，都将对参数产生一定的波动。为量化各因素与参数之间的关系，提高对相似材料物理力学参数的调控效率，鉴于此，对表3中的正交试验数据进行多元线性回归分析。

设y为因变量，xj(j=1, 2, …, m)为自变量，则多元线性回归分析模型[16]为：

令yk(k=1, 2, …, 7)分别表示相似材料的密度、抗压强度、抗拉强度、弹性模量、泊松比、黏聚力和内摩擦角；令x1，x2，x3，x4和 x5分别表示影响相似材料物理力学参数的(重晶石粉+铁精粉)/骨料 、铁精粉/(铁精粉+重晶石粉)、胶结剂含量(占固体总量)、石膏/胶结剂和甘油含量(占固体总量)。为求得最佳常数项a和系数b1，b2，b3，b4和 b5，并使得通过线性回归得到的参数y的误差最小，因此，需要计算各参数的残差平方和，结合式(1)得：

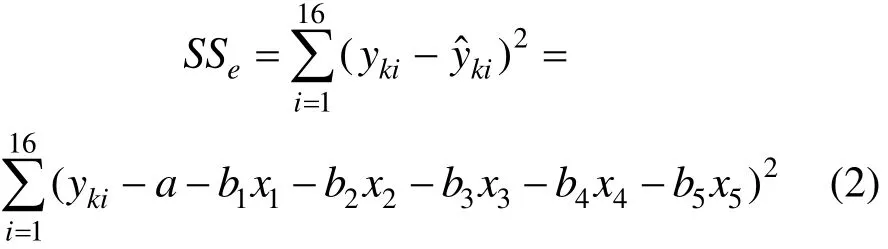
根据最小二乘法原理，要使得残差平方和 SSe值最小，则式(2)应满足以下条件：

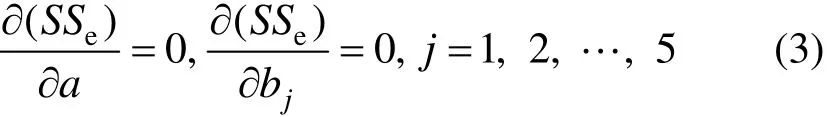
对式(3)整理得下列方程组：

将表3正交试验结果中的密度值及各因素的量值代入式(4)，解得

则密度与各因素之间的线性回归方程为：

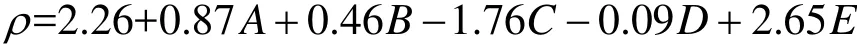
同理可得：

抗压强度与各因素之间的线性回归方程为：

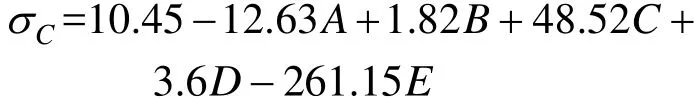
抗拉强度与各因素之间的线性回归方程为：

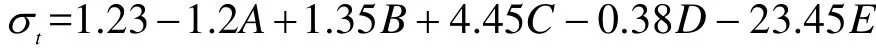
弹性模量与各因素之间的线性回归方程为：

泊松比与各因素之间的线性回归方程为：

黏聚力与各因素之间的线性回归方程为：

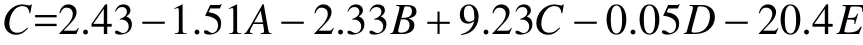
内摩擦角与各因素之间的线性回归方程为：

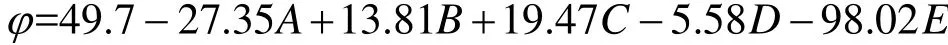
为对比分析线性回归分析结果与试验结果的差异，验证利用线性回归分析方法得到相似材料物理力学参数的可靠性，结合表2和各参数与各因素之间的线性回归方程，得到了各组试验中相似材料物理力学参数的线性回归分析结果，见表4。

由表4中数据可知，通过多元线性回归分析得到的相似材料的物理力学参数与试验结果整体较为接近，表明利用线性回归分析方法构建各因素与参数之间的定量关系，进而可通过各因素的具体量值得到相应相似材料的参数是可行的。

根据表3和表4 得到了各参数的试验结果与线性回归结果更加直观的对比分析图，如图3所示。

由图3可以看出，各参数的试验结果与回归分析结果的变化趋势大体一致，二者吻合良好，同时也证明了利用线性回归分析方法求得相似材料的物理力学参数是可靠的。

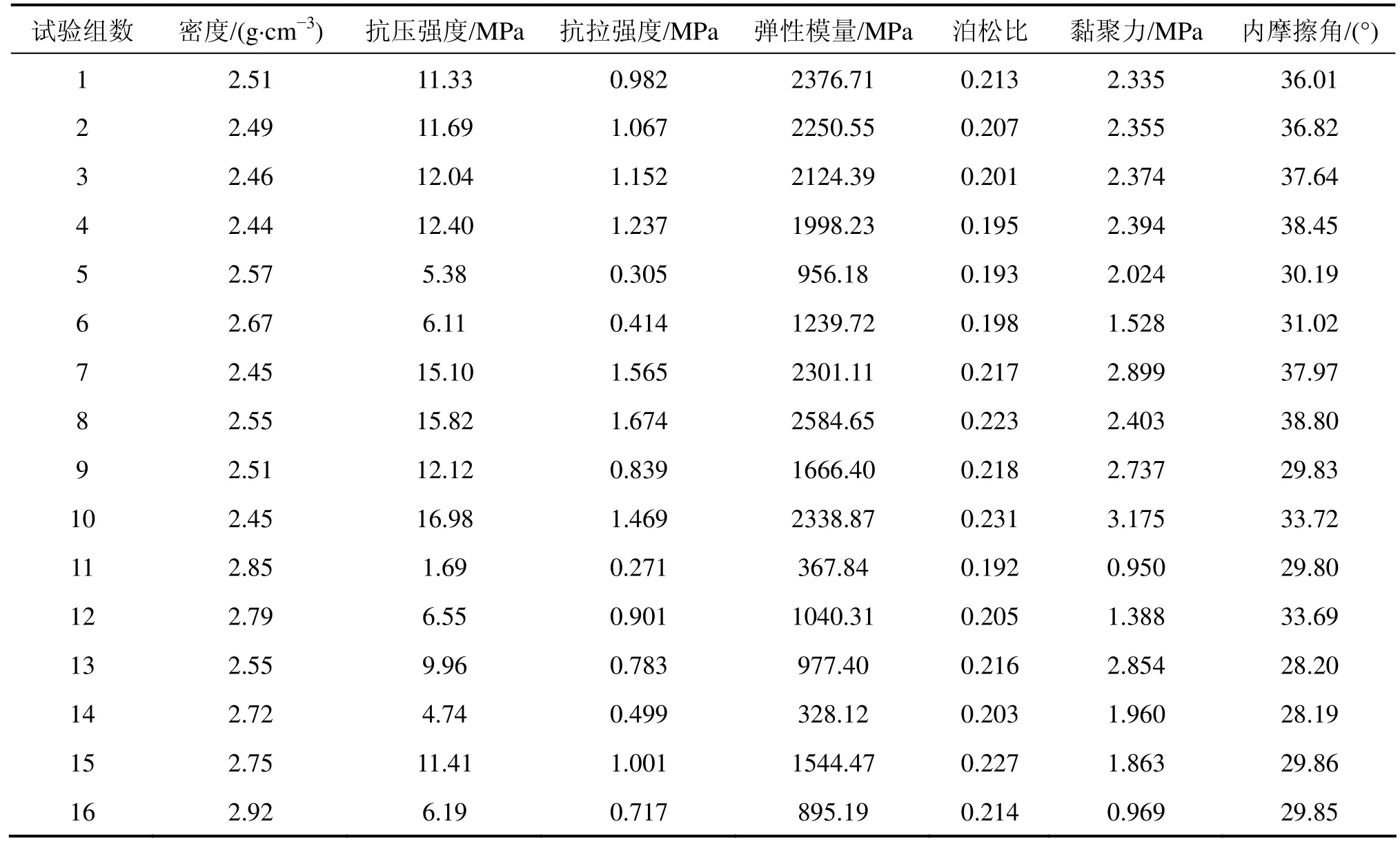
表4 各参数线性回归分析结果Table 4 Linear regression analysis results for each parameter

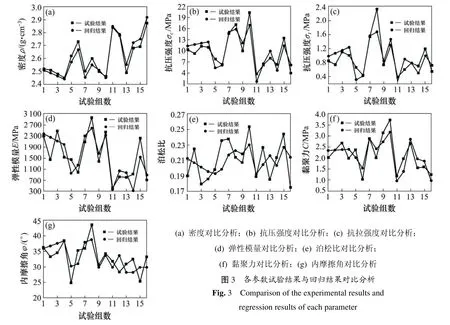
图3 各参数试验结果与回归结果对比分析Fig. 3 Comparison of the experimental results and regression results of each parameter

由上述分析可知，通过求解各参数与影响因素之间的线性回归方程，量化了二者之间关系。因此，当由相似原理确定了模型物理力学参数的前提下，可通过联立上述方程求解出各影响因素的量值，从而能够配制出符合模型试验要求的相似材料，极大地促进了相似材料的配制效率。

2.3 各因素显著性分析

方差分析是用于2个及2个以上样本均数差别的显著性检验，利用方差分析能够判断出各因素对目标参数影响的显著性，指明各因素之间的交互作用，以及显著影响因素的最佳水平，进而可以确定各因素对目标参数贡献的大小[16]。

由于相似材料的物理力学参数受多个因素的共同影响，因此，加大了配制相似材料的难度，倘若知道每个因素对各个参数的影响程度，这无疑能够提高相似材料的配制效率，则有必要对每个因素的显著性进行分析。

各因素的离差平方和SSA为：

式中：n为总试验次数；r为因素的水平数；yi(i=1,2, …, n)为试验结果。

各因素的离差均方 MSA及试验误差均方MSE为：

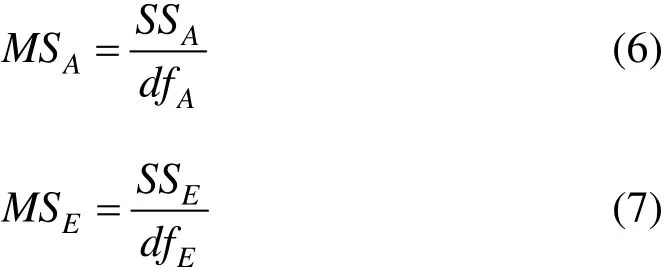
式中：dfA和 dfE为自由度，其中，dfA=r−1，dfE=n−r。则由式(6)和式(7)得各因素的统计量F为：

结合表2与表 3，并联立式(5)~(8)，得出各因素的统计量F，如表5所示。

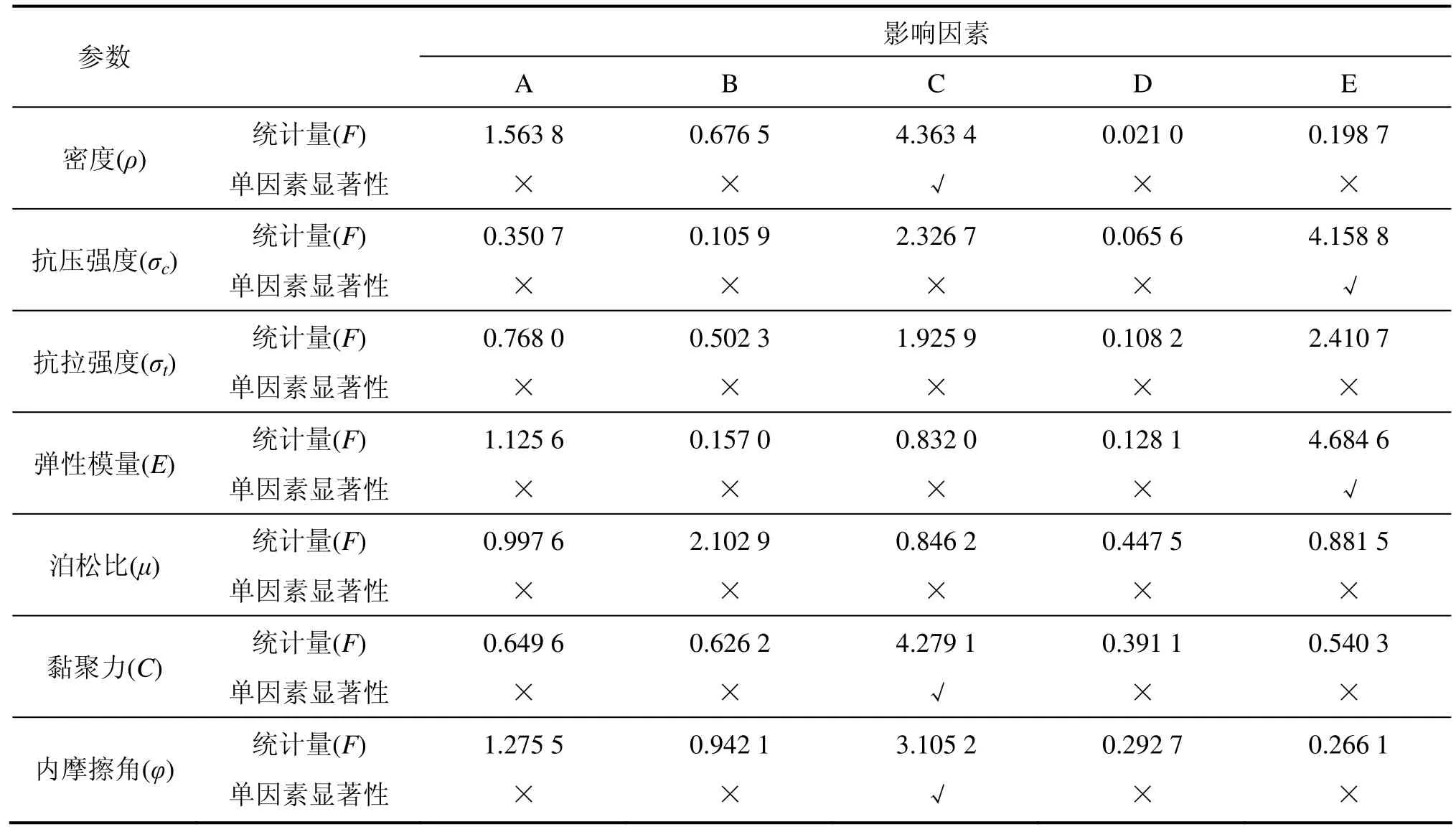
表5 各参数方差分析Table 5 Variance analysis of each parameter

在置信水平α=0.1条件下，查得因素显著性临界值F(3, 12)=2.61，从表5中可以看出，因素C即胶结剂含量对密度影响显著，其他因素影响均不显著，根据F的大小可看出，各因素对相似材料密度影响的主次顺序为 C＞A＞B＞E＞D，即胶结剂含量＞(重晶石粉+铁精粉)/骨料＞铁精粉/(铁精粉+重晶石粉)＞甘油含量＞石膏/胶结剂；因素E即甘油含量对抗压强度影响显著，其他因素影响均不显著，根据F的大小可以看出，各因素对相似材料抗压强度影响的主次顺序为 E＞C＞A＞B＞D，即甘油含量＞胶结剂含量＞(重晶石粉+铁精粉)/骨料＞铁精粉/(铁精粉+重晶石粉)＞石膏/胶结剂；从表中可以看出，所有因素对抗拉强度影响均不显著，根据F值的大小可以看出，各因素对相似材料抗拉强度影响的主次顺序为 E＞C＞A＞B＞D，即甘油含量＞胶结剂含量＞(重晶石粉+铁精粉)/骨料＞铁精粉/(铁精粉+重晶石粉)＞石膏/胶结剂；因素E即甘油含量对弹性模量影响显著，其他因素影响均不显著，根据F的大小可以看出，各因素对相似材料弹性模量影响的主次顺序为 E＞A＞C＞B＞D，即甘油含量＞(重晶石粉+铁精粉)/骨料＞胶结剂含量＞铁精粉/(铁精粉+重晶石粉)＞石膏/胶结剂；从表中可以看出，所有因素对泊松比影响均不显著，根据F的大小可以看出，各因素对相似材料泊松比影响的主次顺序为 B＞A＞E＞C＞D，即铁精粉/ (铁精粉+重晶石粉)＞(重晶石粉+铁精粉)/骨料＞甘油含量＞胶结剂含量＞石膏/胶结剂；因素 C即胶结剂含量对黏聚力影响显著，其他因素影响均不显著，根据F值的大小可以看出，各因素对相似材料黏聚力影响的主次顺序为 C＞A＞B＞E＞D，即胶结剂含量＞(重晶石粉+铁精粉)/骨料＞铁精粉/(铁精粉+重晶石粉)＞甘油含量＞石膏/胶结剂；因素C即胶结剂含量对内摩擦角影响显著，其他因素影响均不显著，根据F的大小可以看出，各因素对相似材料内摩擦角影响的主次顺序为 C＞A＞B＞D＞E，即胶结剂含量＞(重晶石粉+铁精粉)/骨料＞铁精粉/(铁精粉+重晶石粉)＞石膏/胶结剂＞甘油含量。

综上分析可知，通过方差分析能够确定出各影响因素对相似材料物理力学参数影响的显著性，从而可针对影响显著的因素进行重点调控，进而能够有的放矢地进行相似材料的配制。此外，通过控制显著因素，可以较快地获得试验所需的相似材料配比，为后续的模型试验奠定基础。

3 结论

1) 不同配比相似材料的物理力学参数具有较大的取值范围，能够满足大部分岩体模型试验对相似材料的要求，为以浇筑方式制作试验模型的岩质类相似材料配制提供了参考。

2) 通过对相似材料的物理力学参数与影响因素进行线性回归分析，量化参数与因素之间的关系，当由相似原理确定试验模型的参数后，可准确计算出各因素的量值，极大提高了相似材料的配制效率。

3) 由方差分析可知，胶结剂含量对相似材料的密度、黏聚力和内摩擦角影响显著，甘油含量对相似材料的抗压强度和弹性模量影响显著，各影响因素对相似材料的抗拉强度和泊松比影响均不显著。

参考文献：

[1] 刘晓敏, 盛谦, 陈健, 等. 大型地下洞室群地震模拟振动台试验研究(Ⅰ): 岩体相似材料配比试验[J]. 岩土力学, 2015, 36(1): 83−88.LIU Xiaomin, SHENG Qian, CHEN Jian, et al. Seismic shaking table test for large-scale underground cavern group (Ⅰ): Proportioning test on similar materials of surrounding rock[J]. Rock and Soil Mechanics, 2015,36(1): 83−88.

[2] 关振长, 龚振峰, 陈仁春, 等. 基于正交设计的岩质相似材料配比试验研究[J]. 公路交通科技, 2016, 33(9):92−98.GUAN Zhenchang, GONG Zhenfeng, CHEN Renchun,et al. Experimental study on mix proportion of rock similar material based on orthogonal design[J]. Journal of Highway and Transportation Research and Development,2016, 33(9): 92−98.

[3] 史小萌, 刘保国, 亓轶. 水泥石膏胶结相似材料在固-流耦合试验中的适用性[J]. 岩土力学, 2015, 36(9):2624−2630.SHI Xiaomeng, LIU Baoguo, QI Yi. Applicability of similar materials bonded by cement and plaster in solidliquid coupling tests[J]. Rock and Soil Mechanics, 2015,36(9): 2624−2630.

[4] Kim S H, Burd H J. Model testing of closely spaced tunnels in clay[J]. Geotechnique, 1998, 48(3): 375−388.

[5] DENG X N, JIANG Y H, WANG Z J, et al. Similitude material confecting of tunnel model in shaking table test[J]. Applied Mechanics and Materials, 2014, 51(2):1774−1778.

[6] Jacoby W R, Schmeling H. Convection experiments and the driving mechanism[J]. Geologische Rundschau, 1981,70(1): 207−230.

[7] Iskander M, LIU J. Spatial deformation measurement using transparent soil[J]. Geotechnical Testing Journal,2010, 33(4): 16−23.

[8] 张强勇, 李术才, 郭小红, 等. 铁晶砂胶结新型岩土相似材料的研制及其应用[J]. 岩土力学, 2008, 29(8):2126−2130.ZHANG Qiangyong, LI Shucai, GUO Xiaohong, et al.Research and development of new typed cementitous geotechnical similar material for iron crystal sand and its application[J]. Rock and Soil Mechanics, 2008, 29(8):2126−2130.

[9] 韩伯鲤, 陈霞龄, 宋一乐, 等. 岩体相似材料的研究[J].武汉水利电力大学学报, 1997, 30(2): 6−9.HAN Boli,CHEN Xialing, SONG Yile, et al. Research on similar material of rock mass[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1997,30(2): 6−9.

[10] 李树忱, 冯现大, 李术才, 等. 新型固流耦合相似材料的研制及其应用[J]. 岩石力学与工程学报, 2010, 29(2):281−288.LI Shuchen, FENG Xianda, LI Shucai, et al. Research and development of a new similar material for solid-fluid coupling its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 281−288.

[11] 马芳平, 李仲奎, 罗光福. NIOS模型材料及其在地质力学相似模型试验中的应用[J]. 水利发电学报, 2004,23(1): 48−51.MA Fangping, LI Zhongkui, LUO Guangfu. NIOS model material and its use in geomechanical similarity model test[J]. Journal of Hydroelectric Engineering, 2004, 23(1):48−51.

[12] 刘汉香, 许强, 王龙, 等. 地震波频率对岩质斜坡加速度动力响应规律的影响[J]. 岩石力学与工程学报,2014, 33(1): 125−133.LIU Hanxiang, XU Qiang, WANG Long, et al. Effect of frequency of seismic wave on acceleration response of rock slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 125−133.

[13] 赖杰, 郑颖人, 刘云, 等. 双排抗滑桩抗震性能振动台试验研究及数值分析[J]. 中南大学学报(自然科学版),2015, 46(11): 4307−4315.LAI Jie, ZHENG Yingren, LIU Yun, et al. Shanking table test studies and numerical analysis of double-row anti-slide piles under earthquake[J]. Journal of Central South University (Science and Technology), 2015, 46(11):4307−4315.

[14] 蒋昱州, 姜小兰, 王瑞红, 等. 乌东德双曲拱坝三维地质力学模型试验研究[J]. 长江科学院院报, 2014,31(10): 139−145.JIANG Yuzhou, JIANG Xiaolan, WANG Ruihong, et al.Research on three dimensional geomechanical model test of Wudongde double curvature arch dam[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(10):139−145.

[15] 范刚, 张建经, 付晓, 等. 含泥化夹层顺层岩质边坡动力响应大型振动台试验研究[J]. 岩石力学与工程学报,2015, 34(9): 1750−1757.FAN Gang, ZHANG Jianjing, FU Xiao, et al. Large-scale shaking table test on dynamic response of bedding rock slopes with silt intercalation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(9): 1750−1757.

[16] 李云雁, 胡传荣. 试验设计与数据处理[M]. 北京: 化学工业出版社, 2010: 82−127.LI Yunyan, HU Chuanrong. Experimental design and data processing[M]. Beijing: Chemical Industry Press, 2010:82−127.