分类预测中变量相对重要性的度量

高 峰，姚新武

（北京特恩斯市场研究咨询有限公司，广州 510055）

0 引言

分类预测，是指通过向现有数据学习，建立算法模型使之对未来新进入数据的分类归属做出预测。分类预测是数据分析、数据挖掘和机器学习中的重要课题，广泛应用于自然科学和社会科学的诸多领域。事实上，自20世纪90年代诞生以来就一直在互联网领域发挥着核心作用的推荐系统(Recommender systems)即是分类预测的应用典范。例如，在电商平台广为使用的协同过滤(Collaborative filtering)推荐技术，其主要思想是：利用已有用户群过去的行为或意见预测当前用户最可能喜欢哪些东西或对哪些东西感兴趣[1]。无论是通过关联规则挖掘，还是利用概率论方法实现的协同过滤，原理上都是简单地将预测问题看作分类问题。

一个“好”的分类预测模型，应当是选取合适个数(或尽可能少)的变量而达到一个令人满意(或尽可能高)的预测准确度，前者确保模型符合简约原则(Principle of parsimony)，后者则是模型具有实用性的基本考量——是被广泛接受的衡量模型优良性的评估目标。通常，预测准确度以正判概率(即正判率)作为度量，也经常被称为回判正确率，因为正确与否只能针对现有或过往数据进行预测后作出结论，对新数据的预测则无法验证。影响预测准确度的两个关键因素：一是预测变量集的选取，其直接决定了总体可分性[2]，即构成总体的各组分类间差异的显著性；二是合适的方法的选择和运用，目前备受推崇并有较多成功实践的是基于混合策略(Hybrid strategy)构建的系统[1]，既结合不同算法和模型的优点，又克服它们自身的缺陷和问题，最终实现系统改进。

在获得分类预测模型之后，研究人员经常还会面临另一个待解问题：各预测变量对模型构建的相对重要性或贡献度分别有多大？典型地，这是一个动因分析(Driver analysis)问题，通过分析帮助了解影响目标变化的关键因素及其相对强弱，然后籍此制定应对未来变化的策略、或对有限的资源做出更有效的配置。可用于动因分析的方法有很多，既有贝叶斯信念网络(BBN)、结构方程模型(SEM)等变量间较复杂关系的处理，也有基于(偏)相关分析、回归分析的线性模型，以及较简单的基于计数或描述性统计的方法，如贝叶斯条件概率等。

然而，在构建分类预测模型的实践中，引入通常的动因分析方法解决上述问题往往并不可行，主要面临以下两个疑难：一是，预测变量数量多、且由混合尺度测量。二是，引入通常的动因分析将造成与分类预测之间的彼此孤立。因此，当需要对预测变量的相对重要性做出决策时，需要这样的一种分析技术：它的评估目标应与模型整体优良性的度量相一致，而且适用于常见的混合测量尺度的情形。本文发现，Shapley值分解或分配，也称为Shapley值法，正是满足这样期望的一个方法，它来源于合作博弈论。在合作博弈中，全部或若干参与者，常被称为局中人，以合作形式构成一个联盟(Coalition)，目标是最终实现联盟利益的最大化，Shapley值分解则用于解决在实现这一目标过程中每一个局中人的收益分配问题。将Shapley值分解应用于分类预测中变量相对重要性的度量，类比地，局中人为预测变量、联盟为基于一个变量集的预测模型、联盟利益为模型的预测准确度，即分析目标可转化为：在实现模型的预测准确度达到优良性水平的过程中，预测变量的贡献度分别为多少。

1 基于Shapley值的预测准确度的分解

1.1 Shapley值分解

由Shapley L.S.(1953)[3]首先提出，Shapley值用于度量在多人合作博弈中每一个局中人为利益联盟所带来的效益或价值的大小。例如，在一个n人合作对策问题中，全体n个人的合作即构成一个利益联盟，事实上他们之中任何若干人(≤n)的合作形式也均是一个联盟，这样的联盟子集也称为组合，对联盟利益都会产生一定的效益。理解Shapley值的关键就在于，该值通过确定一个局中人在包含其的所有可能组合中的效益，然后综合作为其对联盟利益的总体效益的衡量。

在合作博弈中，局中人之间的利益活动是非对抗性的，因此局中人出现在一个组合中不会引起效益的减少。这样，全体n个人的合作将为利益联盟带来最大效益，Shapley值分解即是将这个最大效益“公平地”分配到每一个局中人的一种方案。具体地，局中人j在联盟中分配到的Shapley值(即带来的效益)是：

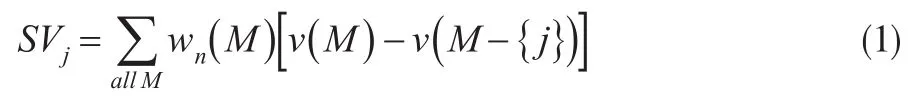
其中，wn( )M为加权因子，表明局中人j在组合M中的比重，定义为：

在式(1)和式(2)中,n是联盟中局中人的总数，m是组合M中局中人的个数，v()是用于度量每一个联盟组合的效益的特征函数，符号M-{j}表示组合M中除去局中人j。

式(1)中[v(M)-v(M-{j})]是组合M(包含局中人j)与组合M-{j}(从M中除去局中人j)的效益的差值，其意义相当于局中人j对组合M带来的“边际效益”。因此，Shapley值可简单地解释为：在各种可能的联盟组合下，局中人对该组合的边际贡献之和除以各种可能的组合数。

尽管显得简单和自然，Shapley值分解实际上是一个公理化方法，Shapley L.S.(1953)[3]提出并证明Shapley值满足如下公理体系：

（1）有效性：所有局中人的效益之和等于总的(即最大化的)联盟利益，即SV(all)=∑SVj；

（2）对称性：局中人具有平等关系，即当局中人的编号改变时，其分配所得份额不受影响；

（3）可加性：如果a和b为任意两个博弈，那么，SVj(a即局中人在博弈中所得份额是在两个分博弈中所得份额的和。

同时，Shapley L.S.(1953)[3]指出，在满足上述公理体系的前提下，对任何n人合作博弈的收益分配，Shapley值分解是唯一解。

1.2 净效应和分类预测中准确度的分解

“边际效益”的另一个常用且对等的说法是“净效应(Net effect，简写为NEF)”。这样，作为“局中人对所有可能联盟组合下的边际贡献之和”的加权度量，Shapley值实际上是局中人对联盟利益的贡献大小的“净效应”分配。按照上面Shapley值“有效性”公理，即有：

在应用层面，具有这样的良好解释性的方法深受欢迎——因为很多动因分析方法仅致力于考察潜在影响因素的主效应，同时研究和在数量上厘清诸多因素之间的交互效应往往比较困难——这极大地拓展了Shapley值分解的实践领域。其中，尤以对回归建模中拟合优度诊断指标决定系数(即R2)的Shapley值分解的应用最为广泛，用来评估多个自变量对因变量的影响程度的净效应(此时，自变量之间的多重共线性不再是影响模型拟合的问题)，且正在逐渐形成一个新的理论分支，即Shapley值回归(Shapley Value Regression，简写为SVR)。

Lipovetsky等(2001)[4]和Wan(2002)[5]是SVR应用的代表力作，前者讨论了Shapley值分解应用于多变量回归分析的优势以及对最终回归系数的校正，后者着眼于收入不平等分配的决定因素的分解。此后，将SVR推广到非线性或其他连接函数(例如Logistic回归)的情形。

在Lipovetsky等(2001)[4]构建SVR时，将一个自变量(即局中人)“进入-剔出”回归方程(即联盟/组合)带来的R2增量视为式(3)中的净效应——意即式(1)中特征函数v()以R2为度量，因此式(1)可改写为：

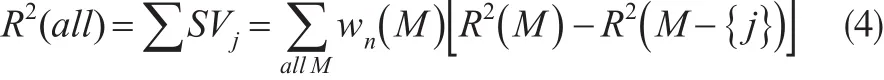
在分类预测中，预测准确度(标记为AR)是衡量模型整体优良性的评估指标。受式(4)启发，本文将一个预测变量“进入-剔出”分类预测模型(即联盟/组合)带来的AR增量视为式(3)中的净效应——意即式(1)中特征函数v()以AR为度量，那么适用于回归方程中R2分解的式(4)可进一步改写为：

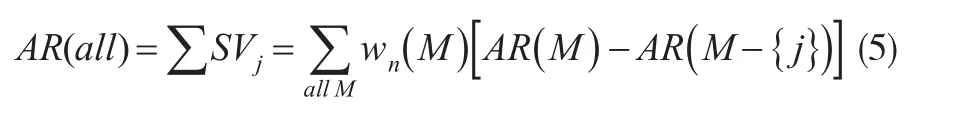
式(5)即是在分类预测建模中对预测准确度的Shapley值分解。

至此，本文不但在原理上类比地将Shapley值分解引入到分类预测建模中，而且在算法上将二者有机地结合在一起，从而可顺理成章地应用Shapley值分解来解答分类预测中变量相对重要性度量的问题。

2 数值算例

2.1 数据说明与变量选取

案例数据来自2016年2月底执行的一个有关智能手机的用户满意度调查，以网络推送问卷方式执行，最终有效样本数为5598个。调查采用净推荐值(Net Promoter Score，即NPS)作为满意度度量，即根据用户对新近购买的智能手机的“推荐可能性”(以0～10分尺度测量，0=一定不会推荐，10=一定会推荐)，将其区分为推荐型(9～10分)、消极满意型(7～8分)和贬低型(0～6分)三类客户之一，而NPS在数值上等于总体客户群体中推荐型与贬低型客户占比的差值。项目研究目的之一是识别出影响用户满意度(即NPS)的关键驱动因素，并建立预测模型，以帮助企业前瞻性的预判用户口碑和采取适当的先期介入举措等。

由上不难理解，NPS预测建模其实就是一个分类预测问题，其基本逻辑是：如果每一个客户能够以一个较高的预测准确度被归入上述三类群体，即客户群占比确定，那么就可以准确地计算出NPS值。

经过变量预处理(转换或再编码、异常值识别等)，以及组均值相等性检验、逐步法筛选变量、判别分析的交叉验证等数据分析过程[6]，识别出21个变量(见表1前3列)对用户满意度有显著影响,尝试引入其他变量进入模型对预测准确度的提升几无贡献。

表1 影响用户满意度(即NPS)的关键驱动因素

以这21个变量作为预测变量集，采用“混合策略”[7]——组合使用判别分析(基础方法)和贝叶斯分类器算法(对“疑似错判”样本的修正方法)，本文构建了NPS预测模型，将现有样本正确归入三类客户群的整体准确率为78.4%(单独用判别分析时的正判率为76.7%)。

2.2 预测变量相对重要性的度量：Shapley值分解及算法简化

显然，上述的21个预测变量由混合尺度测量，譬如年龄(X1)为次序变量、上一部手机品牌(X2)为名义变量、产品特性体验（X7至X19）等由5分尺度测量可视为类连续变量，采用通常的以测量预测变量与目标变量之间取值关联性的方法进行动因分析存在困难。接下来，本文以前述的Shapley值分解法(即式(5))进行动因分析，即着力回答这样的问题：各预测变量对分类预测模型构建的相对重要性或贡献度分别有多大？

Shapley值分解作为动因分析方法，是将变量对所构建模型的贡献大小的“净效应”进行合理分配。在分类预测建模中，预测变量对模型的贡献以其对模型的整体优良性(即预测准确度)的提升效果作为度量。

然而，Shapley值分解需要检视“所有可能组合”，对上述含21个变量的集合，所有可能的组合数为一个很大的数。这意味着，如果以判别分析作为分类预测的算法（为使叙述简单化，Shapley值分解仅用于对判别分析正判率的分解），本文将需要运行约210万个判别分析过程以取得它们的正判率数据，任务相当艰巨和耗时，有时得不偿失。因此，本文提出以下两种用于算法简化的方法，既满足分析的实效，又能改善算法效率。

2.2.1 算法简化：建立嵌套的路径模型，分层进行Shapley值分解

路径分析(Path analysis)，有时也称为隐变量分析(Latent variable analysis)、结构方程模型(Structural Equation Model)等，是多变量统计分析中的常用方法，广泛应用于诸多领域。通常，路径分析的首要任务是构建一个路径图：（1）路径图依赖于研究人员对待解问题的专业理解，应当符合直觉、简单和易于理解、具有实际意义(与业务发展模式相匹配)，有助于问题的简单化和聚焦，（2）路径图认为诸多变量对目标变量的作用并非完全地具有同一性，而是结构化的(非单一的)和层级化的(有些是直接的、有些是间接的)。

本算例即建立了一个嵌套层次的路径模型（见下页图1），图中五个区块分别对应五个维度变量（见表1后2列），通常被称为潜变量（Latent variable），其中“产品特性体验（G3）”未作为潜变量表示出来，以避免与测量变量“总体使用体验（X4）”重复，同时本文认为这组变量对“品牌偏好程度（X5）”和“性价比感知（X6）”也有影响作用。为了简单化，同时本文并不是采用结构方程模型拟合图1（见下页），因此未用圆圈和方框去区分潜变量和测量变量，也未列出误差项。类似处理方式也出现在文献[8]中，通过构建分层结构循序实施Shapley值分解，先将收益分配的不平等归因于若干首要因素，而后将首要因素的影响分解为与其相联系的次要因素的贡献。

与结构方程模型一般采用偏最小二乘法(PLS，适用于连续变量)、一次拟合得到整个模型的路径系数的分析方式不同，本算例引入Shapley值分解，逐层分析预测变量或维度变量对模型的预测准确度改善的“净效应”，仍然以判别分析作为分类预测方法。

先看第一层：包含4个维度变量（G1/G2/G4/G5）。此时，由它们构成的预测变量集的所有可能组合数为24-1=15，显然是一个完全可承受的数量。本文并不打算去数量化这些维度变量，而是认为：当考虑维度变量时，由它们派生出的预测变量应“同时地”进入/剔出模型。具体地，所有15个变量集组合、以及各自所包含的预测变量显示在表2(前2列)。

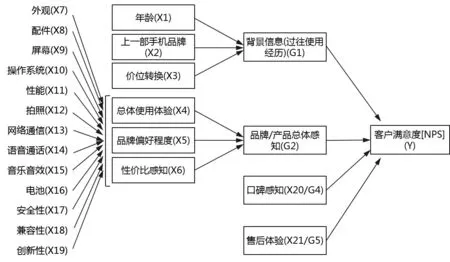
图1 驱动因素对用户满意度(即NPS)的影响机制的路径模型

表2 路径图第一层的变量集组合及判别分析的正判率

对每一个变量集组合，运行判别分析,得到模型的正判率(见表2最右列)。这样，根据式(5)即可计算出维度变量G1的Shapley值：

按式(6)同样计算得到维度变量G2/G4/G5的Shapley值：

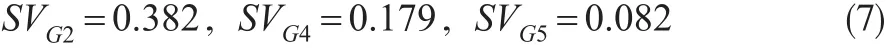
如前所述，Shapley值分解度量个体对联盟的“边际贡献”或“净效应”，因此可加总后折算为占比数值：

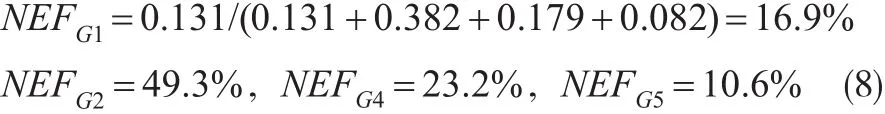
式(8)数值的实际含义是：将背景信息(过往使用经历)、品牌/产品总体感知、口碑感知和售后体验等视为影响用户满意度(即NPS)的四大维度因素，它们的贡献度(从统计学角度应理解为对NPS数据变化的解释度)分别为16.9%、49.3%、23.2%和10.6%。

接着看第二层的“背景信息(过往使用经历)”区块：包含3个预测变量(X1/X2/X3)，它们进入/剔出模型所对应的预测变量集的所有可能组合数为23-1=7。因是比较区块内各变量对模型的相对贡献度，则区块外变量可视为始终保留在模型中。对7个变量集组合分别运行判别分析,得到模型正判率，即可计算出预测变量X1/X2/X3的Shapley值：

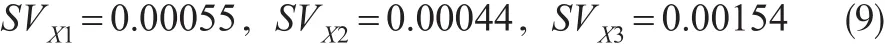
加总后折算为“区块内”占比数值：

同样处理第二层的“品牌/产品总体感知”区块(此时区块外变量，包括X7/…/X19，均视为始终保留在模型中)，计算出区块内变量X4/X5/X6的Shapley值、并加总后折算为“区块内”占比数值：

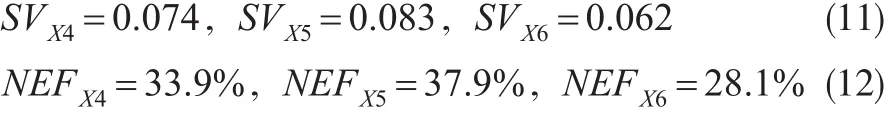
2.2.2 算法简化：仅纳入多变量的低阶组合

尝试处理第三层：包含13个预测变量(X7/…/X19)，它们被视为X4/X5/X6的底层影响因素。问题再次出现，它们进入/剔出模型所对应的预测变量集的所有可能组合数为213-1=8191，也是一个很大的数，执行这么多次模型仍将非常耗时。本文的解决方法是：不由于检视“所有可能组合”的算法理想，而是仅纳入多变量的低阶组合。实践中，因遍历“所有可能组合”存在技术障碍或时间花费代价高昂而采取此种简化操作的情形并不少见，譬如：（1）当计算多变量之间的偏相关系数时，往往只计算至一阶或二阶组合；（2）当考察多个自变量/预测变量对目标变量的影响关系时，如果需要考虑交互效应，通常也仅涉及一阶交互项。同时，很多的验证性工作表明，变量之间关系大都由主效应或较低阶交互效应(或变量间组合)主导，较高阶交互效应的影响关系趋弱。

本算例实际用到至多五阶组合，即仅考虑不超过5个变量的那些组合，而舍弃6个或更多变量的组合。五阶及更低阶组合的个数为仍然较大但已属可控。除了需要耗费显著多的时间(约数小时)运行这么多次判别分析、得到模型正判率之外，处理过程与上述无异，计算出变量X7/…/X19的Shapley值、并加总后折算为“区块内”占比数值：NEFX14=6.7%，NEFX15=4.4%，NEFX16=3.7%，NEFX17=9.4%，NEFX18=10.1%，NEFX19=8.9% (14)

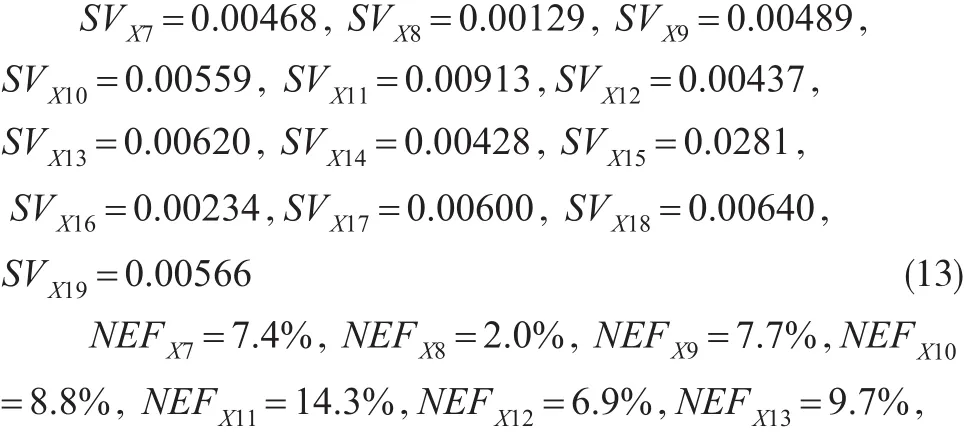
当变量个数较多时，仅纳入低阶组合参与分析可以是一种提升效率的近似算法。当然，如果具有良好的编程能力和高性能的硬件设备，以及较高的时间花费容忍度，可以考虑纳入更高阶或“所有可能组合”至算法过程。

2.3 算例结果

将式（8）、式（10）、式（12）和式（14）的计算结果标注到图1的相应路径上（见图2），即完成以客户满意度（即NPS）为目标变量的分层结构的动因分析。基于此结果，仍可进行更多的“深挖”分析，譬如29岁以下年轻人较30岁以上人士对产品满意度明显更低等，以获得更多的市场洞察。

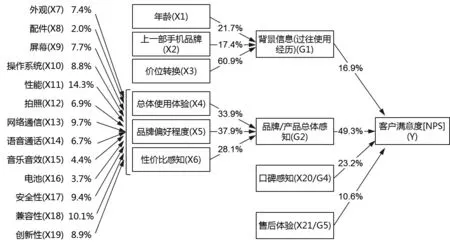
图2 基于分层结构的用户满意度(即NPS)的动因分析

需要注意的是，图2中数值不应视为通常的路径模型的拟合系数，而应从Shapley值作为“净效应”分配的原理出发，理解为区块内变量对区块变量(或下一层指标对上一层指标)的数值变化的影响程度的相对大小，有时也可理解为区块内变量对区块变量达到当前状态的贡献度的相对大小。

3 结论

本文运用起源于合作博弈论的Shapley值法，开创性地通过分解与每一个预测变量相关的正判率来度量它们的相对重要性。Shapley值法易于理解、其结果具有良好解释性，在诸多领域得到应用；此外，Shapley值法至少还有以下两个方面的好处：

（1）Shapley值法兼容于任何分类预测方法，甚至是基于“混合策略”的组合方法。Shapley值法仅作用于预测准确度的分解，独立于构建分类预测模型时使用的算法本身，譬如本文算例将判别分析作为分类预测方法，但如果以贝叶斯分类器算法构建预测模型，Shapley值分解同样适用。不过，Shapley值分解需要得到不同预测变量集下的预测模型的准确度数据，因此，过于复杂的分类预测算法(譬如基于“混合策略”的组合方法)将在一定程度上影响Shapley值法的使用效率。

（2）Shapley值法适用于任何测量尺度的变量集。Shapley值法既不需要另外构建模型、也不必引入某种动因分析方法，因此无涉任何一个变量的测量尺度。这一特性让Shapley值法显得卓尔不群，因为处理混合尺度的测量数据集是很多动因分析方法(譬如回归分析)的软肋。

局限在于，Shapley值法需要遍历变量集的“所有可能组合”：当变量个数较多时，它们的组合数就非常庞大，导致Shapley值法运算量极大、时间花费巨大。此时，宜采用一些简化算法，譬如本文介绍的两种，以改善Shapley值法的使用效率、平衡时间成本。

参考文献:

[1]Jannach D,Felfernig A,Zanker M,et al.推荐系统(Recommender Systems:An Introduction)[M].北京：人民邮电出版社，2013.

[2]潘志文，汪国强.判别分析中基于总体可分性的变量选择[J].华南理工大学学报:自然科学版，2010，29(11).

[3]Shapley L S.A Value for n-Person Games:in Kuhn H.W.,Tucker A.W.(Eds.),Contribution to the Theory of Games,II[R].Princeton,NJ:Princeton University Press,1953.

[4]Lipovetsky S,Conklin M.Analysis of Regression in Game Theory Ap⁃proach[J].Applied Stochastic Models in Business and Industry,2001,(17).

[5]Wan G.Regression-based Inequality Decomposition:Pitfalls and a Solution Procedure[R].WIDER Discussion Paper,2002.

[6]张文彤.SPSS统计分析高级教程[M].北京:高等教育出版社,2004.

[7]高峰，姚新武.分类预测中正判率的改进方法[J].统计与决策，2017,(12).

[8]Shorrocks A F.Decomposition Procedures for Distributional Analysis:A Unified Framework Based on the Shapley Value[J].The Journal of Economic Inequality,2013,(11).