指标及权重均为混合数据类型的广义灰靶决策方法
2018-04-26马金山
马金山
(河南理工大学 能源科学与工程学院,河南 焦作 454000)
0 引言
自邓聚龙提出灰靶决策方法以来[1],许多学者对其进行了研究改进。随着决策理论与方法研究的深入,决策方案的指标值也由单纯的实数值拓展为混合属性指标值。混合属性灰靶决策方法也随之产生,这进一步增强了该方法的适用性。灰靶决策方法的核心是求各决策方案对于靶心的靶心距,并以靶心距作为各方案优劣决策的依据。决策方案指标值为确定性实数的灰靶决策方法其对靶心距的获取主要是采用距离法,如采用欧氏距离法或马氏距离法[2,3]。而混合属性灰靶决策方法对靶心距的获取可以分为两类:一类是采用距离的方法进行处理,主要是采用欧氏距离,也包括基于距离的变形方法求靶心距[4-9];另一类是采用向量的方法进行处理,这称为混合属性广义灰靶决策方法[10,11]。广义灰靶决策方法是基于传统的灰靶决策方法,在遵循其基本原理不变的基础上提出的一种方法,其基本的计算过程与传统方法有所不同[10-12]。以向量为基础的混合属性广义灰靶决策方法,由于所采用的微小向量考虑了不确定数的不确定性信息,且在运算过程中信息的失真较少所以比前者更优。已有的混合属性广义灰靶决策方法所涉及的各指标权重值均为确定性的实数,不存在用不确定性数表示的权重。但当各指标属性的权重含有不确定数表示的混合权重值时则更为复杂,主要体现在:一是权重数据本身含有的不确定性增加了决策的不确定性;二是如何将不确定性的权重值与各指标值进行综合集成;三是如何使得均存在不确定性的权重和指标值在运算时信息失真少,决策结果更符合实际。
为此,对指标及权重均为混合数据类型(本文仅考虑实数、区间数、三角模糊数及梯形模糊数)的广义灰靶决策方法进行研究。本文以二元联系数向量为基础,分别求各决策方案指标向量与靶心指标向量的接近度并经归一化,待求出确定化后的权重再进行各单指标接近度的集成;而混合数据值的权重则统一转化为二元联系数向量后进行求模运算,并经归一化后作为各指标的确定性权重。然后将确定化后的权重数据与已经求得的各单指标的规范化接近度进行集成,以综合接近度进行最终的排序决策。
1 基本理论
定义1:记R为实数域,称x͂为一个模糊数,则[xL,分别为模糊数的区间数、三角模糊数和梯形模糊数的表现形式,其参数xL,xM,满足
定义2:记R为实数域,称A+Bi为二元联系数,其中A,B∈R,i∈[-1,1],A表示确定的项,B表示不确定的项,i是一个变动的项,它的存在统一了模糊数的确定和不确定性。
定义3:设xˉ和v分别是x͂的p(p≥2)个参数值的平均值和偏差值,则称:
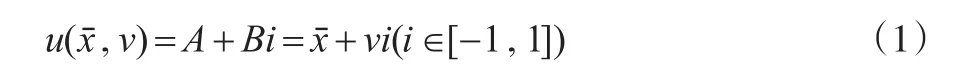
为x͂的p个参数的均值-偏差值联系数,简称均值-偏差值联系数。其中xˉ,S,ms以及v分别由式(2)至式(5)得到:


式(2)至式(5)中均值xˉ可以看作是关于x͂的p(p≥2)个参数的相对确定性(集中性)的测度,标准差S或最大极差ms是关于x͂的p个参数的相对不确定性(离散性)的测度,可以取其最小值代表x͂的不确定性部分,记为v,称为偏差值[10,15]。
定义4:均值-偏差值联系数u(xˉ,v)中的均值xˉ和偏差值v的相互作用则可以反映到基于集对分析的二维确定-不确定空间(Determinacy-uncertainty,简称D-U空间)。当u(xˉ,v)=xˉ+vi表示D-U空间的向量时,“i”仅代表该项是不确定分量的符号,不再代表取值的变化[13,14]。
图1是二维确定-不确定空间的示意图,其中xˉ为确定性度量,v为不确定性度量,其中r是向量u(xˉ,v)的模,即有

图1 确定-不确定空间[15]
2 决策方法
2.1 指标及权重均为混合数据类型的广义灰靶决策难点
指标及权重均为混合数据类型的广义灰靶决策的难点在于:一是不同类型的权重数值无法直接进行集成以获得综合的接近度;二是简单地将不同类型的数据转化为确定性的权重则容易产生较大的误差,如仅取模糊数的参数的均值代表模糊数则容易造成信息的失真而影响决策的精度;三是如何采用一种统一、简单的方法实现含有不确定性权重值融入综合的接近度。因此指标权重为混合属性值的wt(t=1,2,…,m)包含了不确定性的内容。其中wt可以为实数或模糊数,当其取值为模糊数时,其可为区间数、三角模糊数或者梯形模糊数形式,即有:
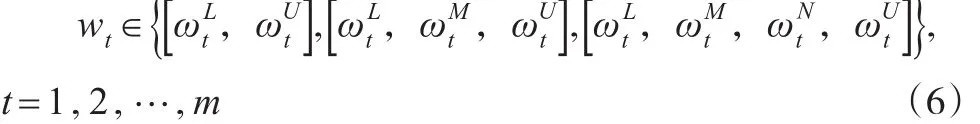
此时一般有下面的关系式成立:

2.2 指标及权重均为混合数据类型的广义灰靶决策方法的求解思路
结合已有的研究,拟以二元联系数作为混合属性广义灰靶决策方法的基础,求解思路见图2所示。
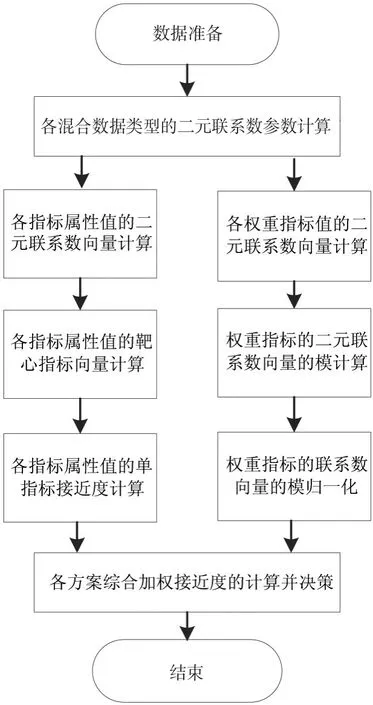
图2求解思路
2.3 指标及权重均为混合数据类型的广义灰靶决策方法的决策步骤[10]
2.3.1 所有方案指标及权重数据均转化为二元联系数向量
采用前述的公式(1)至公式(5)将不同类型的数据值的指标及权重统一转换为二元A+Bi的联系数形式,并认为每个联系数是二维确定-不确定空间中的向量。其中实数认为是二元联系数中的确定项为该数值本身,不确定项为0,即为A+0i的形式。设转化后的各指标向量为Ust=Ast+Bsti(s=1,2,…,n;t=1,2,…,m)。
2.3.2 求出各指标属性的靶心指标向量
确定了各属性下各方案指标的向量Ust=Ast+Bsti(s=1,2,…,n;t=1,2,…,m),则可以确定决策方案各指标属性的灰靶靶心,见式(8)。
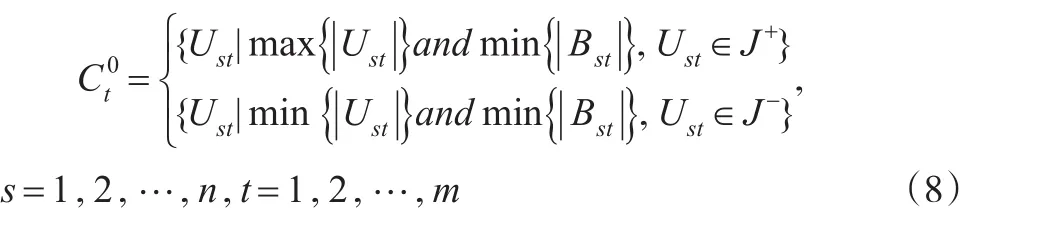
上述公式表明,对于效益型指标,即求指标向量模的值最大对应的指标向量为靶心,当有几个向量的模相等时,选择不确定性小的指标向量作为靶心;成本型指标即求向量模的值最小对应的向量为靶心,当有几个向量的模相等时,则选择不确定性小的指标向量为靶心。
2.3.3 决策方案各单指标接近度的求解
定义5:设rst为基准指标向量Yst的模,pst为指标向量Xst在Yst上的投影,则:

为投影值pst与基准指标向量Yst的模rst的距离,称为接近度,pst和rst的计算公式可参考文献[10]。
2.3.4 各属性下单指标接近度的归一化处理
前面所求出的各方案的各属性指标向量与靶心指标向量的接近度彼此是不同的,属性之间不具有可比性,因此,这里需要针对各个属性下的单指标接近度(广义靶心距)dst进行归一化。归一化的接近度zst的计算公式见(10)。

2.3.5 求各指标属性的确定性权重
(1)计算各属性权重的联系数向量的模
已经确定了各个指标属性的指标权重向量,则可以计算各指标权重向量的模。这里实际上是将各混合数据类型的指标权重的二元联系数向量的模视为确定性的权重的代表值。因为所有的权重二元联系数向量是在同一D-U空间内,而其模则代表了其各自在该空间中的重要性大小,故此可以认为各权重联系数向量的模可以代表其确定的权重。而该确定性权重同时包含了不确定数的确定性和不确定性部分。
(2)指标权重向量模的归一化处理
前述步骤所求出的各指标属性的权重模未经规范化,与通常意义上的各指标权重有所差异。为此,对步骤(1)求出的权重数据运用公式(10)进行归一化处理,得到通常意义下的权重值。
2.3.6 求得各决策方案加权的综合接近度
已经获得各个指标属性的权重,那么可以求出各个方案的综合接近度,即:

根据NEs的值由小到大的顺序进行排序,即可得到各决策方案的优劣。
3 算例分析
3.1 数据来源
对战术导弹进行评估,采用6个指标分别是命中精度(km)、弹头载荷(kg)、机动性能(km.h-1)、价格(106g)、可靠性和可维护性,分别用A1至A6表示[8]。其中A1和A4为成本型指标,其余为效益型指标。4个方案分别用S1至S4示,数据见表1所示。
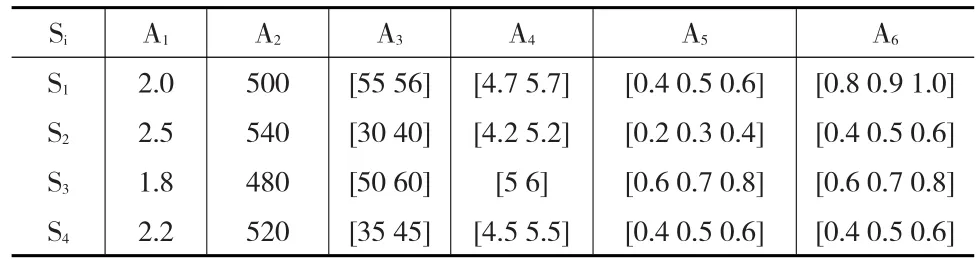
表1 各方案的指标值
3.2 决策过程
(1)计算各决策方案各指标的二元联系数参数
由表1中数据采用公式(2)至公式(5)可以求出各指标的用于二元联系数计算的参数见表2。

表2 均值、标准差和最大偏差
(2)将所有方案的指标均转化为二元联系数
根据公式(1)至公式(5),基于表2数据将表1所示的各指标值转化为联系数向量的形式见表3。

表3 转化后的各指标二元联系数向量
(3)求各指标属性的单指标靶心向量
由于A1和A4为成本型指标,而其余为效益型指标,根据公式(8)可以得到各指标属性的靶心向量为:C0=(1.8+0i 540+0i 55+5i 4.7+0.5i 0.7+0.1i 0.9+0.1i)
(4)求各单指标的接近度
采用公式(9)和公式(10)可以求得各决策方案各指标向量与靶心指标向量的单指标归一化接近度见表4所示。
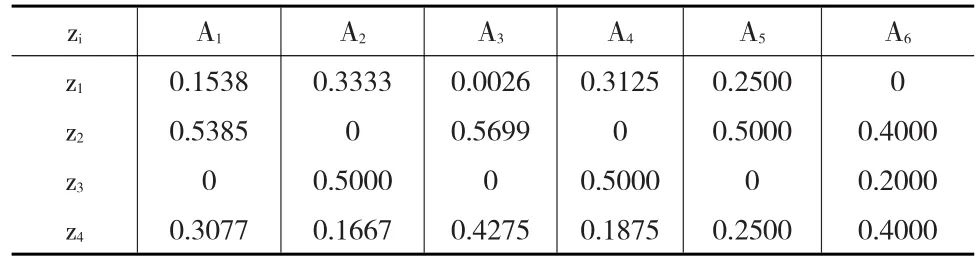
表4 各单指标的标准化接近度
(5)混合数据类型指标权重的确定化
设给定各个指标属性的不确定性权重分别为:W=([0.16 0.18 0.2],[0.18 0.2 0.22],0.1,[0.18 0.2 0.22 0.24],[0.14 0.18],[0.12 0.16]),其中不确定数表示的权重的数据的参数下限值的和为小于或等于1,而上限的参数值的和为大于或等于1。
首先,要计算各个混合数据类型权重的参数见下页表5所示。
其次,将各权重表示为二元联系数向量的形式如下页表6所示。

表5 所有指标权重参数的均值、标准差和最大偏差

表6 指标权重的二元联系数向量
然后,求出各个指标权重向量的模见表7。

表7 指标权重的二元联系数向量的模
采用公式(10),可以对各指标权重的模进行归一化处理即可得到通常意义下的各确定的指标权重W=(0.1818,0.2017,0.1004,0.2124,0.1618,0.1419)。
(6)获得综合接近度并进行决策
运用公式(11),采用确定化的权重 W=(0.1818,0.2017,0.1004,0.2124,0.1618,0.1419)可得到各决策方案综合加权的接近度为:INE=(0.2023,0.2928,0.2354,0.2695)。
根据综合接近度越小越优的原则,可以得到各决策方案的排序为:S1≻ S3≻ S4≻ S2。
4 结论
本文得到了如下结论:
(1)将混合属性广义灰靶决策方法的权重由确定性的实数扩展为含有不确定模糊数的混合数据类型,进一步增强了其适用性。
(2)基于二元联系数向量分别对混合数据类型的指标和权重进行处理,待求出各决策方案归一化单指标接近度及确定化权重后再进行决策方案的集成,具有决策思路清晰、计算方法统一、简便的优点。
(3)以混合数据类型权重的二元联系数向量的模作为其确定化权重的方法考虑了模糊数的确定性和不确定性方面具有信息失真少、决策准确的特点,但仍有进一步探讨的余地。
参考文献:
[1]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[2]党耀国,刘国峰,王建平等.多指标加权灰靶的决策模型[J].统计与决策,2004,(3).
[3]王正新,党耀国,杨虎.改进的多目标灰靶决策方法[J].系统工程与电子技术,2009,31(11).
[4]Luo D,Wang X.The Multi-Attribute Grey Target Decision Method for Attribute Value Within Three-Parameter Interval Grey Number[J].Applied Mathematical Modelling,2012,36(5).
[5]Song J,Dang Y G,Wang Z X,et al.The Decision-making Model of Harden Grey Target Based on Interval Number With Preference Infor⁃mation on Alternatives[J].Journal of Grey System,2009,21(3).
[6]关欣,孙贵东,衣晓等.基于关联系数靶心距的混合多属性识别[J].航空学报,2015,36(7).
[7]曾波,刘思峰,李川等.基于蛛网面积的区间灰数灰靶决策模型[J].系统工程与电子技术,2013,35(11).
[8]沈春光,党耀国,裴玲玲.混合型多指标灰靶决策模型研究[J].统计与决策,2010,(12).
[9]党耀国,刘思峰,刘斌.基于区间数的多指标灰靶决策模型的研究[J].中国工程科学,2005,7(8).
[10]Ma J S,Ji C S.Generalized Grey Target Decision Method for Mixed Attributes Based on Connection Number[J].Journal of Applied Math⁃ematics,2014,(8).
[11]Ma J S.Grey Target Decision Method for a Variable Target Centre Based on the Decision Maker’s Preferences[J].Journal of Applied Mathematics,2014.
[12]马金山,孙静.基于决策者偏好的正负靶心灰靶决策方法[J].科技管理研究,2014,34(23).
[13]赵克勤.二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用[J].智能系统学报,2008,3(6).
[14]赵克勤.基于集对分析的不确定性多属性决策模型与算法[J].智能系统学报,2010,5(1).
[15]Ma J S,Ji C S,Sun J.Fuzzy Similar Priority Method for Mixed Attri⁃butes[J].Journal of Applied Mathematics,2014,(1).
