一种基于C#实现的生产多批次数量值的选值算法∗

刘益申 管文建

（上海天臣防伪技术股份有限公司互联网事业部 上海 200433）

1 引言

现在广大商家在售卖自己的产品时，通常会采取购买有奖的促销方式，即消费者在购买商品后可获得额外奖品，有奖促销行为已经成为现代商业营销的一种重要手段［1］。过去传统的兑奖方案是将实体兑奖卡放入商品包装内，消费者在购买商品后，获取包装内的兑奖卡，凭兑奖卡找商家进行相应兑奖。随着互联网和移动互联网的兴起，公开号为CN202472742U的实用新型专利设计了一种网络验证兑奖信息系统［1］，公开号为CN103150806A的发明专利发明了一种网络的发票自助兑奖方法［2］，很多商家也开始使用类似的新型电子兑奖方案，即消费者在购买商品后，根据商品包装内的电子兑奖码，通过网络进入商家的网上兑奖平台，通过输入兑奖码来进行兑奖。比起传统的实体兑奖卡兑奖方案，电子兑奖方案使消费者不受时间、地域的限制，随时进行兑奖［3］，免去实体兑奖卡的制作成本，另外将整个兑奖流程交由商家后台的计算机程序来管理，使传统的兑奖方案数字化，使兑奖卡与商品实现数字关联，并可根据市场销售情况动态设置奖项内容，最大有利于市场营销。

然而电子兑奖方案也存在一定风险，即仅仅通过网上的兑奖平台输入兑奖码来确认消费者是否中奖是不够安全的，通常兑奖码由若干位数字和字母构成，由于位数固定，那么兑奖码所有的排列情况也是确定的，这样在商家的网上兑奖平台上，存在某些人不购买商品却通过猜测恰好输入正确兑奖码从而假冒兑奖的情况，毫无疑问，这样的行为不仅损害了本该中奖的消费者利益，也给商家带来严重的经济损失。公开号为CN101894343A的发明专利也指出当前公开的电子兑奖方案不能完全杜绝假冒兑奖的缺陷［4］，该发明专利虽然提出了一种通过事先采集消费者指纹和增设兑奖密码来进行兑奖验证的方法，但该方法实施过于繁琐复杂，极大增加了消费者的购物流程和验证兑奖系统的复杂度，实用性不高。

本文针对电子兑奖方案存在的风险，提出一种简单易实现的方案，即在商家生产商品时应使用多批次生产，并设计了批次数量值的选值算法，最后使用了C#语言和Math.Net开源数学库实现了该算法，可在绝大多数情况下计算出较优的批次数量值范围，供商家来参考。

2 使用多批次生产来降低猜中兑奖码的概率

首先假设电子兑奖码由d位（d＞0）数字（0～9）或者英文字母组合构成（英文字母不区分大小写，由于英文字母I和O和数字的1和0外形十分相似，为了避免给消费者带来混淆，将不包含字母I和O），因此兑奖码的每一位有10种数字和24种英文字母选择，共34种选择，根据这种兑奖码的长度和场合数计算中的“相乘法则”［5］，d位兑奖码共有34d种组合。然后假设商家一次性共生产了n（n＞0）件商品，每件商品都含有唯一的兑奖码，所以共有n个正确的兑奖码。另外假设商家采用的是购买即中奖的促销方式，即只要消费者在网上兑奖平台输入正确的兑奖码，就视为成功中奖。在这种情况下，猜测1次就猜对兑奖码的概率为P1，这种猜测符合古典概型［6］的定义：

这个概率随着n值递增，当n值较大时，概率也会较大，考虑到很多商家的产品产量非常大，因此这种带给商家的风险不可小视。

然而商家在生产商品时使用多批次生产时，即将生产的商品并非一次性投入市场而是将商品分批次投入市场可以降低这种风险。现在来计算采取多批次生产后，某个时刻猜测一次就成功猜测出商品兑奖码的概率。虽然无法确定猜中的兑奖码来源于哪个批次，但这个猜中的商品兑奖码一定来源于所有批次中的一个批次，基于这个简单的事实，利用全概率公式［6］，设商家共分为m个（2≤m≤n）批次生产，每个批次的商品投入市场的时间相同，每个批次的商品数量为可得某个时刻猜测1次就猜中兑奖码的概率为

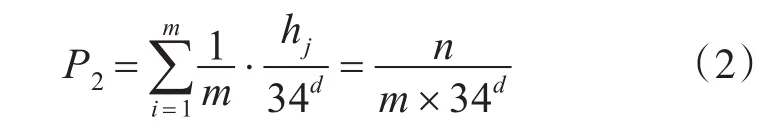
可见P2和n成正比，和d以及m成反比，P2与式（1）中的P1相比后，可以得出：

因此采用多批次生产可降低猜测1次就猜中商品兑奖码的概率m倍。

3 多批次生产对海量猜测兑奖码的影响

很多时候，某些人会安装一些计算机脚本程序，这些脚本程序会自动海量尝试猜测兑奖码，并可能得到大量正确的商品兑奖码。这种行为给商家带来的危害更大。那么多批次生产是否也能降低这种危害，是很值得考虑的。

设计算机脚本每次尝试都是独立的，那么现在来计算一下恰好猜中n个兑奖码出现的概率。在概率学中，如果在一次试验中只关心某个事件是否发生，那么称这个试验为贝努利试验，相应的数学模型称为贝努利概型［6］。另外，在n重贝努利实验中，设随机变量X表示n次试验中事件A发生的次数，可以得出X的概率函数为［6］

称这个随机变量X服从参数为n，p的二项分布，记做X～B（n，p），其中0＜p＜1。当n值较大，n×p值适中时，通常当n≥10，p≤0.01时，这个时候可以利用泊松定理［6］来使用泊松分布来近似模拟二项分布，设 λ=np ，0＜p＜1，k≥ 1：

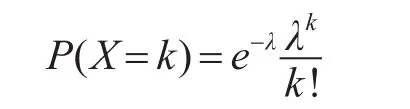
称这个随机变量X服从参数为λ的泊松分布［6］，记作X～P（λ），其中，λ＞0。

为了更方便并直观的比较采用多批次生产前后的猜中多个兑奖码的概率区别，将使用Octave来模拟绘制两者的分布图像。Octave作为一款免费软件，语法和Matlab十分相似，主要用于数值计算［7］。这里假设商家共生产了20000000件商品，兑奖码为6位长度，通过计算机脚本程序尝试猜测兑奖码1000次，根据式（1），猜测1次猜中兑奖码的概率np=1000×0.0129=12.9。如果商家采用10个生产批次，采用10个生产批次后，根据式（3），猜测1次猜中兑奖码的概率np=1000×0.00129=1.29。这里由于 n≥10，p≤0.01，因此可使用泊松分布来观察猜中n个兑奖码的概率分布，使用Oc⁃tave来模拟该分布的情况如图1。

图1 2种不同的生产方式下的概率函数值

从图1可以看出，虽然采用多批次生产时，猜中兑奖码的数量大于5的概率更低，但猜中兑奖码的数量小于5的概率明显更高，由此可见采用多批次生产后，可降低猜测1次猜中兑奖码的概率，但在使用计算机脚本程序海量尝试时，可能存在猜中某些数量兑奖码的概率反而会更高的现象，因此一个合适的批次数量值选值是非常重要的。

4 批次数量值的选值算法设计

现在设商家共生产了C（C＞0）件商品，使用计算机脚本程序至多尝试nx（nx≥1）次，未采用多批次生产时的猜测1次猜中兑奖码的概率为 p1（0＜p1＜1），猜中 k（1≤ k≤ nx）个兑奖码的概率为 P1，采用多批次生产后，分为m（2≤m≤C）个批次，猜测1次猜中兑奖码的概率为 p2（0＜p2＜1），猜中k（1≤k≤nx）个兑奖码的概率为 P2，根据式（3），p2=p1/m。如果商家采用多批次生产，现在需要选择一个合适的m值，即这个m值能够始终使P2≤P1。

由于有效的批次数量值m≥2并且小于等于产量总值，直观地，可以遍历每个可能的批次数量值，计算在该批次数量值下，P2≤P1是否成立。如果成立，那么这就是一个合适的批次数量值。但这样的做法耗时较多，效率较低，特别是当商家的产量总值较大的时候，需要遍历的数目也会非常大。为了提高算法的效率，可做如下优化：

结论1 无论是使用二项分布还是泊松分布计算概率函数值，如果要使 P2≤P1，那么显然P2(k=1)≤P1(k=1)也必然成立。另外如果能在使用计算机脚本程序尝试nx的情况下使P2(k=1)≤P1(k=1)，那么当尝试次数小于nx时（使用 n=nx-t来 表 示 ，1 ≤ t≤ nx-1） ，P2(k=1)≤P1(k=1)仍然成立。

证明如下：

对于二项分布：

∴当n=nx-t时，P2(k=1)≤P1(k=1)

现在观察P(k=1)的单调情况，根据n和 p1的值，可分为两种情况：

1）当0＜n＜10或者 p1＞0.1时，使用二项分布的概率函数值更好。

无论是否采取多批次生产，恰好猜中1个兑奖码的概率为

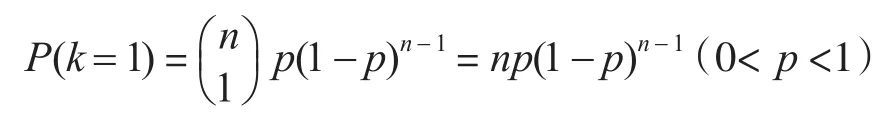
此时对P(p)求导：

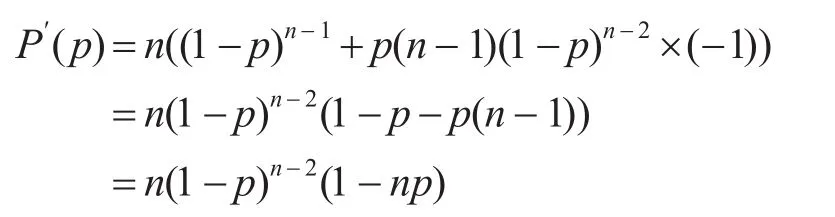
结论2 当k=1时，P(p0=)是P（p）上的一个最大值，并且在np＜1时递增，在np＞1时递减。

根据这个结论2和结论1，可以首先计算nxp1的值，如果小于1，那么为了使采用多批次生产后能 使 P2(k=1)≤P1(k=1)，只 需 nxp2≤nxp1，即可使m=2，3，4，…，C，即批次数量值从2到总产量值C都可以满足条件。

结论3 现在考虑猜中的兑奖码个数为k（2≤k≤ nx）时，当满足 P2(k=1)≤P1(k=1)时，是否仍然能使P2≤P1。结论是肯定的，证明如下：

综上，可以得出当nxp1≤1时，批次数量值范围为[2 ，C ]上的所有整数。

现在考虑当nxp1＞1时的情况，根据结论2，当k=1时，P(k=1)在 np＞1的时候是递减的，而p2＜p1，所以如果 nxp2仍然大于1，那么 P22(k=1)将会大于P1(k=1)，这是不符合要求的。因此符合要求的nxp2必然小于1。根据结论2，P(k=1)在np＜1的时候是递增的，p最小值为，所以当批次数量值取总产量值C时，P2(k=1)是最小的。

如果此时的P2(k=1)＞P1(k=1)，那么说明在这个尝试次数nx下，合适的批次数量值并不存在，这样就继续考虑尝试次数为nx-1的情况下，合适的批次数量值是否存在。

如果此时的P2(k=1)=P1(k=1)，那么说明批次数量值取总产量值C是唯一合适的批次数量值。

如果此时的P2(k=1)＜P1(k=1)，则说明合适的批次数量值存在，并可能存在多个，所以这时需要找到一个最小的能使P2(k=1)≤P1(k=1)的值m1，根据结论3，说明m1是个合适的批次数量值。又因为之前得出符合要求的nxp2必然小于1并且根据结论2，P(k=1)在np＜1的时候是递增的，比m1更大的批次值必能使 p2更小也能使P(k=1)更小，所以最终的批次数量值范围为[m1，C ]上的所有整数。

通过这些结论，在nxp1＞1的情况下，可以预先判断出合适的批次数量值是否存在或者只存在唯一合适的批次数量值，省去了依次遍历每个可能的批次数量值，提高了算法的时间效率。

综上这就是当0＜n＜10或者 p1＞0.1时，使用二项分布的批次数量值选值的主要流程。

2）当n≥10并且 p1≤0.1时，设 λ=np（λ＞0），二项概率可使用泊松分布的概率函数值来近似，泊松分布在n值较大时的计算相比二项分布更加简单，可以减少一定的计算量。

无论是否采取多批次生产，恰好猜中1个兑奖码的概率为

此时对 P(λ)求导：

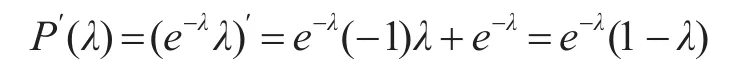
由此可知，唯一的驻点λ0=1，即np=1。当λ＜λ0时（即 np＜1时），P′(λ)＞0，而当p＞ λ0时（即 np＞1时），P′(p)＜0 ，由此可说明［8］：

结论4 当k=1时，P(λ0=1)是 P(λ)上的一个最大值，并且在np＜1时递增，在np＞1时递减。

根据这个结论4和结论6，可以首先计算nxp1的值，如果小于1，那么为了使采用多批次生产后能 使 P2(k=1)≤P1(k=1)，只 需 nxp2≤nxp1，即可使m=2，3，4，…，C，即批次数量值从2到总产量值C都可以满足条件。

结论5 现在考虑当猜中的兑奖码个数为k（2≤k≤nx）时，当满足 P2(k=1)≤P1(k=1)时，是否仍然能使P2≤P1。结论是肯定的。

证明如下：

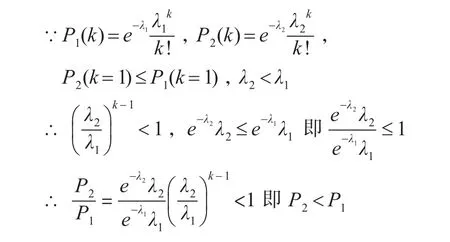
综上，可以得出当nxp1≤1时，批次数量值范围为[2 ， C ]上的所有整数。

现在考虑当nxp1＞1时的情况，将结论4、结论5和使用二项分布的结论2、结论3进行类比，可以发现接下来的流程和使用二项分布完全一致。这里不再赘述。

综上这就是当n≥10并且p1≤0.1时，使用泊松分布的批次数量值选值的主要流程。

5 基于C#和Math.Net库实现多批次生产的批次数量值选值算法

根据第3节的批次数量值选值的流程，现在使用C#语言和Math.Net库通过计算机程序来实现该批次数量值的选值算法。Math.Net是.Net平台上一款开源的基础数学工具箱，主要分为几个子项目，其中的Math.Net Numerics的核心功能是数值计算，主要是提供日常科学工程计算相关的算法，包括一些特殊函数，线性代数，概率论，随机函数，微积分，插值，最优化等相关计算功能［9］。另外程序将基于WPF 技术，WPF（Windows Presentation Foundation）是基于。Net的新一代界面开发平台［10］，商家用户可以方便地在界面上进行相关输入操作，输入生产总产量、兑奖码长度、猜测尝试最大次数之后，可得出相应的批次数量值范围，商家可根据实际的生产情况综合考虑，决定最后的批次数量值。

调用Math.net其中的Binomial和Poisson类，可以非常方便地进行相应的二项分布和泊松分布的概率函数值计算。

调用Poisson类：

Poisson newPoi=new Poisson（oldLambda/currentTryBatch⁃Number）；

double newP=newPoi.Probability（1）；

调用Binomial类：

Binomial newBin=new Binomial（oldp/currentTryBatchNum⁃ber，n）；

double newP=newBin.Probability（1）；

另外根据第3节的论述，在查找一个最小的能使 P2(k=1)≤P1(k=1)的批次值m1的过程中，根据第3节的结论2和结论4，P(k=1)在np＜1时是递增的，也就是有序的，而在有序数列中二分查找最为常用［11］，因此可以使用二分查找，可以极大提升查找的效率。代码如下：

///＜summary＞

///二分查找法确定最小的批次数量值使P（k=1）小于原来

///＜/summary＞

///＜param name=“oldP1”＞p，即未采用多批次生产，猜中兑奖码的概率＜/param＞

///＜param name=“oldLambda”＞np，n为尝试次数＜/param＞

///＜param name=“startNum”＞当前查找的批次数量值的下界＜/param＞

///＜param name=“endNum”＞当前查找的批次数量值的上界＜/param＞

///＜returns＞＜/returns＞

private int PoiSelectFirstCorrectBatchNumber（double oldP1，double oldLambda，int startNum，int endNum）

｛

int currentTryBatchNumber=（startNum+endNum）/2；//确定用于比较的折半点

Poisson newPoi=new Poisson（oldLambda/currentTry⁃BatchNumber）；

double newP=newPoi.Probability（1）；//计算泊松分布的概率函数值P（k=1），即当np=oldLambda时猜中一个兑奖码的概率

Poisson newPoiCheck=new Poisson（oldLambda/（currentTryBatchNumber-1））；

double newPCheck=newPoiCheck.Probability（1）；

if（newP ＜=oldP1）//使用 currentTryBatchNumber作为批次数量值，P（k=1）是否小于原来

｛

if（newPCheck ＞ oldP1）//使 用 currentTryBatch⁃Number-1作为批次数量值，P（k=1）是否大于原来

｛

return currentTryBatchNumber；//说 明 current⁃TryBatchNumber是一个符合要求的最小的批次数量值，返回

｝

else

｛

endNum=currentTryBatchNumber-1；//说明可以找到比currentTryBatchNumber更小的符合要求的批次数量值

PoiSelectFirstCorrectBatchNumber（oldP1， old⁃Lambda，startNum，endNum）；//继续查找

｝

｝

else

｛

startNum=currentTryBatchNumber+1；//该 cur⁃rentTryBatchNumber不符合要求，过小

PoiSelectFirstCorrectBatchNumber（oldP1，oldLamb⁃da，startNum，endNum）；//继续查找

｝

return 0；

｝

整个程序的流程如下（使用二项分布和泊松分布的流程一致，这里的流程不再作出）：

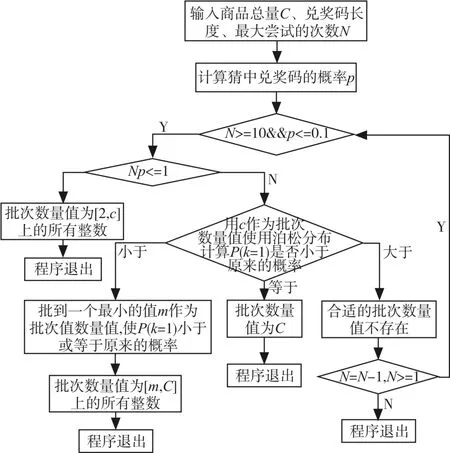
图2 批次数量值选值算法流程图

该批次数量值的选值算法主要优势在于：

1）较好的时间复杂度。二项分布的计算有时相当麻烦，计算量相当大［12］。在最大尝试次数和猜中兑奖码的概率符合相应条件的情况下，使用泊松分布来近似二项分布的概率函数值以简化计算，对尝试次数和猜中兑奖码的概率的乘积进行预先判断，时间复杂度最高不超过O（N2），最短只需O（1）。在查找最小符合要求的批次数量值时使用了二分查找，也大大优化了算法的时间效率。

2）较好的空间复杂度。如果合适的批次数量值存在，根据第3节的论述，最后的批次值为C或[2 ， C ]或[m1，C ]，对于 [2 ， C ]或[m1，C ]，只用一个最小的批次数量值2或者m1存储结果，实质表示从2或者m1到总产量值C的一个范围，极大减少了内存占用。

该批次数量值的选值算法主要局限性在于：

1）程序要求商家用户输入尝试猜测次数的最大值nx，理想情况下，计算得出的批次数量值可使当尝试猜测兑奖码次数分别为1，2，3，…，nx时，猜中k（1≤k≤nx）个兑奖码的概率降低。但根据图2，在尝试猜测兑奖码次数分别为 nx，nx-1，nx-2，…，nx-i（0≤i≤nx-1）时，符合要求的批次数量值可能不存在，得出的批次数量值只能满足部分尝试次数下，猜中k个兑奖码的概率降低。

表1为程序运行的部分结果。

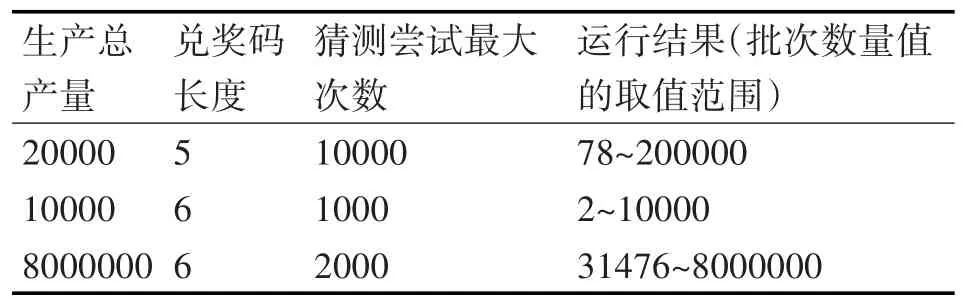
表1 批次数量值选值算法程序的部分运行结果

6 结语

本文指出了现在电子兑奖方案中存在某些人猜测兑奖码假冒兑奖的风险，计算了采用多批次生产后，某个时刻猜中兑奖码的概率，并指出了该概率和兑奖码长度、生产总产量和生产批次数量之间的关系。

另外，本文指出了多批次生产也并非毫无缺点，批次数量的取值问题是很重要的。某些批次数量值可能导致某些人利用计算机脚本程序进行海量尝试兑奖码时，猜中某些个数的兑奖码的概率反而提高了，并利用了一款免费的数学软件Octave通过绘图说明了该问题。

对此，本文进一步提出了一种计算合适批次数量值范围的算法，算法根据二项和泊松分布来计算相关的概率函数值，并利用了二分查找、二项分布和泊松分布相关的单调特性优化了算法，使算法具有较好地时间和空间复杂度，并且最后使用C#编程语言和。Net平台的一款开源数学工具Math.Net实现了该批次数量值选值算法，该算法能够在商家决定生产批次数量时提供一个批次数量值的区间范围，虽然算法存在一定局限性并且仍然无法完全杜绝某些人通过猜测兑奖码假冒兑奖的情况，但可以大大降低这种情况的发生，切实为商家减少经济损失。

［1］ 邓 路 沙.一 种 验 证 兑 奖 信 息 系 统［P］.中 国 ，CN202472742U，2010-10-03.DENG Lusha.Verification award converting information system［P］.China，CN202472742U，2010-10-03.

［2］牛玉山，王培元，段清泉.一种发票自助兑奖的方法［P］.中国，CN103150806A，2013-06-12.NIU Yushan，WANG Peiyuan，DUAN Qingquan.Method of invoice self-service cashing ［P］. China，CN103150806A，2013-06-12.

［3］唐西林，郭海艮.一种基于彩票内容保护的电子彩票方案 的 改 进［J］.计 算 机 应 用 研 究 ，2009，26（4）：1506-1508.TANG Xilin，GUO Haigen.Improvement of electronic lot⁃tery scheme based on protecting content of lotteries［J］.Application Research of Computers，2009，26（4）：1506-1508.

［4］周娟，曾辉，柴亚辉，等.一种有效安全验证的彩票销售兑奖方法［P］.中国，CN101894343A，2010-11-24.ZHOU Juan，ZENG Hui，CHAI Yahui，et al.Effective and safe verification-based lottery ticket sale and prize ex⁃change method ［P］. China， CN101894343A，2010-11-24.

［5］小林道正.概率·统计［M］.卢炜俊，译.上海：上海科学技术文献出版社，2014：4-5.Kobayashi Masae.Probability·Statistics［M］.Translated by LU Weijun.Shanghai：Shanghai Scientific&Technical Publishers，2014：4-5.

［6］同济大学概率统计教研组.概率统计（第三版）［M］.上海：同济大学出版社，2004：24-94.Teaching and research group of probability and statistics at Tongji University.Probability and statistics（Third edi⁃tion）［M］.Shanghai：Tongji University Press，2004：24-94.

［7］Neeraj Sharma，Matthias K.Gobbert.A Comparative Evalu⁃ation of Matlab，Octave，Freemat，And Scilab For Re⁃search and Teaching ［R］.Technical Report HP⁃CF-2010-7.

［8］同济大学应用数学系.微积分（第二版上册）［M］.北京：高等教育出版社，2003：151-153.Department of applied mathematics at Tongji University.Calculus（Second edition，Volume one）［M］.Beijing：High⁃er Education Press，2003：151-153.

［9］数据之巅.开源Math.NET基础数学类库使用（01）综合介 绍 ［EB/OL］. http：//www.cnblogs.com/asxinyu/p/4264638.html.Peak of Math.The general introduction of using open-source basic mathematics library Math.Net（01）［EB/OL］.http：//www.cnblogs.com/asxinyu/p/4264638.html.

［10］王媛娇，孙恺.基于WPF技术的行情分析软件设计与实现［J］.电子设计工程，2014，22（18）：20-22.WANG Yuanjiao，SUN Kai.Design and implementation of market quotations analysis system based on WPF［J］.Electronic Design Engineering，2014，22（18）：20-22.

［11］邹国霞，何南.一种改进的二分查找算法［J］.软件导刊，2010，9（3）：53-55.ZOU Guoxia，HE Nan.An improved binary-search algo⁃rithm［J］.Software Guide，2010，9（3）：53-55.

［12］汪红.用普阿松分布逼近二项分布的误差估计［J］.绵阳师范学院学报，1997，（Z1）：16-18.WANG Hong.The error estimate of using Possion distri⁃bution to approximate Binomial distribution［J］.Journal of Mianyang Normal University，1997，（Z1）：16-18.