多维空间的反最近邻查询算法研究与实现∗

侯晓琳

（北京大学地球与空间科学学院 北京 100871）

1 引言

反最近邻查询是在最近邻查询的基础上提出的一种新的查询方法。反最近邻查询的应用范围也十分广泛，主要集中在网络定位，地理信息系统，地位服务应用，决策系统，文件搜索，数据挖掘等方面。随着计算机技术发展，数据的表现形式和数据量也显著增加。因此，多维空间反最近邻查询算法具有较大的应用价值，成为空间查询研究中的重点和难点。

1973年，由Knuth提出了最近邻查询问题。随后1995年，N.Roussopoulos等提出k最近邻查询问题［1～2］。在最近邻查询的研究过程中，相关领域专家发现了反最近邻查询问题和应用前景，提出了反最近邻查询。2000年由Flip Korn和S.Muthukrish⁃nan提出了反最近邻的相关概念和解决方法［3］。Congjun Yang等又在前面的基础上提出了改进的方法，引入了一种新的数据结构Rdnn-tree［4］。Amit Singh等提出高维反最近邻查询。针对反最近邻查询中存在的问题，相关研究者又提出很多改进方法［5～6］。Rimantas Benetis等提出在平面中连续移动的点的当前位置和期望位置上的RKNN［7］。由Yufei Tao等提出了任意维的反最近邻查询［8］。Mu⁃Hammad Aamir Cheema等提出了一个有效的技术Lazy updates，不断检测反最近邻查询［9］。

由于其具有较大的应用价值，关于反最近邻查询方法仍然在不断地改进，主要在集中在提升查询效率和降低查询成本等方面。

2 空间数据和空间裁剪

2.1 空间数据与R树

采用R树表示和存储空间数据，使用多维元组来表示空间数据对象［10］。每个叶节点中采用指向点数据对象的指针的方式存放多个空间数据点信息。每个非叶节点中存放其所包含的子节点的所有空间数据对象的最小矩形，在三维空间中，即使包含其下所有子节点的最小外包围六面体。在空间查询中使用R树索引结构只需访问少量的节点就能确定数据点，而不需访问所有的数据。

2.2 线性约束查询

线性约束查询目的在于加快搜索的速度，可以快速排除不符合查询条件的空间对象。在N维空间中，定义空间平面，方程为

将空间分成两个半空间，半空间的表示形式为

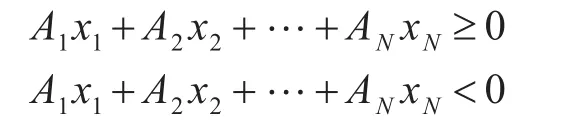
在求N维空间的半空间中，使用两个点作为已知的条件，然后求出表示相应的半空间的线性约束。在实现过程中使用到了点法式，已知在N维空间 中 两 点 p，q，其 中 p=(p1，p2，…，pN) ，q=(q1，q2，…，qN)。可以使用点法式求出一个空间N-1维的平面，这个平面通过线段pq的中点，且与线段pq垂直。pq的中点 p′，该空间N-1维的平面的法向量为 (p1-q1，p2-，q2，…，pN-qN)。由此得到的表示多维空间平面的一个线性约束如下：

其中

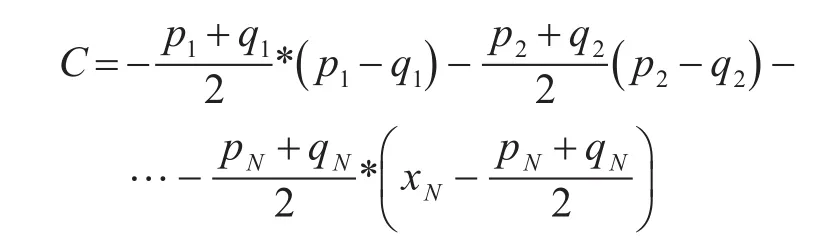
2.3 空间裁剪方法

使用线性约束对原有空间进行裁剪，以三维空间为例，对裁剪方法加以说明。⊥(p ，q )是点q和点p之间的垂直平分面，其中点q是查询点，点p是数据集中的任意点。⊥(p ，q)将整个二维空间分成了两个半空间。显然，在包含点p的半空间中的矩形区域R1中的所有数据点到查询点q的距离都大于到点p的距离，所以R1中的所有点都不是点p的反最近邻点。假如矩形区域R1中的一点 p′，p′的最近邻点是p，不等式成立，所以′不是查询点q的反最近邻点。由此可得，经过垂直平分线⊥(p ，q)划分成两个半空间后，在包含点p半空间中的所有点均不是查询点q的反最近邻点。

图1 三维空间区域的裁剪

3 反最近邻查询算法

3.1 反最近邻查询

给定数据集S和一个查询点q，dist（p，q）定义为两点之间的距离，反最近邻查询就是取得S的一个子集RNN（q）：

反k最近邻查询（RkNN）：给定数据集S和一个查询点q，dist（p，q）定义为两点之间的距离，反k最近邻查询就是取得S的一个子集RkNN（q）：

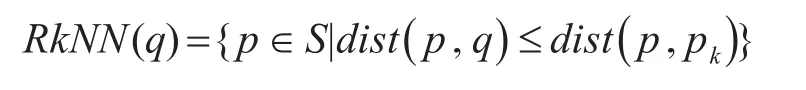
其中 pk∈S，并且 pk表示的是q的k最近邻kNN（q）。

反k最近邻查询算法和反最近邻查询算法相同采用一个两步框架算法，第一步是过滤过程，第二部是提纯过程。在过滤过程中，首先从数据集S中获得一个子数据集S′，作为反k最近邻的候选集。在这个子数据集S′中的数据元素有可能是查询点q的反k最近邻，也有可能不是查询点q的反k最近邻，因此现在获得的子数据集S′还需要获得进一步的处理，下一步的处理过程就是提纯过程。提纯过程需要将子数据集S′中的数据元素进行再次确认，将不是查询点q的反k最近邻的数据元素，即错误命中的数据元素抛弃。经过提纯过程，就可以从子数据集S中获得查询点q的所有的反k最近邻。反k最近邻算法主要由空间裁剪算法，过滤过程和提纯过程算法组成。

3.2 裁剪算法

利用裁剪算法主要目的是检查数据点是否在无效区域内，这里所谓的无效区域指的是一定不包含查询点的反k最近邻的区域。如果数据点在无效区域内，则表示该点不属于目标点的反最近邻。

在点裁剪算法中，输入参数是一个数据点集和一个待裁剪数据点，根据这个数据点集进行裁剪，判断待裁剪点是否是查询点的反最近邻。数据点集（其中 m≥k），待裁剪数据点p，查询点q。这里将数据点集P中的点看作是查询点q的可能反k最近邻，根据这些点，确定无效区域。然后判断待裁剪数据点p是否在无效区域内，点裁剪算法将一个距离值作为算法的输出参数，如果待裁剪点p在无效区域内，则表示数据点p被裁剪掉了，无穷大作为距离值返回；反之，返回点p和点q的距离值。k点裁剪算法的步骤如下：

［步骤1］首先应该求得数据集中任意k个数据点的半空间平面所组成的空间交集。

［步骤2］根据数据集P中数据点的排列顺序来获得k个数据点的交空间，第一个交空间是由数据点 p1，p2，…，pk形成半空间的交空间，这个交空间就是一个无效区域。下一个交空间是由数据点p2，p3，…，pk+1形成的半空间的交空间。以此类推，最后一个交空间是由数据点 pm-k，pm-k+1，…，pm形成的半空间的交空间。可以获得m-k个交空间，这些交空间均为无效区域。

［步骤3］检查待裁剪点p是否在这些交空间中。如果在，则表示点p被裁剪掉，一定不是查询点q的反k最近邻，以无穷大作为输出参数返回。

3.3 过滤算法

在过滤算法中，使用最小堆，集合和R树等数据结构。算法结束后得到两个集合，分别是候选集S和检验集Sr，图2描述过滤算法流程。过滤算法的步骤：

［步骤1］初始化最小堆H，此时最小堆中无任何元素。初始化两个集合，分别是候选集合S和检验集合Sr。

［步骤2］首先将R树中的根插入到最小堆H中。

［步骤3］检查最小堆H是否为空，如果最小堆H为空，即在最小堆H中在无其他元素，那么算法结束。如果最小堆不为空，弹出堆顶元素f。这个堆顶元素f可能是数据点，可能是R树的叶节点，可能是R树的非叶节点。

［步骤4］对这个堆顶元素f进行裁剪操作，采用裁剪算法（trim algorithm），如果算法返回的是无穷大值，那么说明堆顶元素完全被裁剪掉了，把f加入检验集合Sr中，返回步骤3继续执行。反之，接着执行步骤5。

图2 过滤算法流程

［步骤5］判断堆顶元素f的数据类型，根据不同的数据类型进行不同的操作。如果堆顶元素f是数据点，调用裁剪算法判断f是否是可能是查询点q的反最近邻，当裁剪算法返回值不是无穷大值时，就将f加入到候选集合S中，作为q的一个反最近邻，返回步骤3继续执行。如果堆顶元素f是叶节点，对于叶节点f中的每一个数据点做下面的操作：调用裁剪算法判断数据点是否被完全裁剪掉，当数据点被裁减掉时，将数据点插入到检验集合Sr中；当数据点未被裁减掉时，计算出查询点q到数据点之间的距离，将数据点以查询点q到数据点之间的距离为关键值插入到最小堆中。如果堆顶元素f是R树的中间节点，对于中间节点的每一个孩子节点做下面的操作：调用裁剪算法判断孩子节点的最小矩形是否被完全裁剪掉。当裁剪算法返回无穷大值时，说明孩子节点的最小矩形已经被完全裁剪掉了，将该孩子节点插入到检验集合Sr中；当裁剪算法返回值不是无穷大值时，说明在孩子节点的最小矩形中仍有有效区域，将查询点q到孩子节点的最小矩形经过裁剪后得到的有效矩形区域的最小距离作为关键值，将该孩子节点压入最小堆H中。

［步骤六］返回步骤3继续执行。

3.4 提纯算法

提纯算法为每个数据点引进了一个新属性，这个属性作为计数器来用。在提纯算法开始之前，首先需要初始化候选集中每个数据点的计数器属性，初始化的值为k，那么在提纯的过程中，一旦发现候选集中的一个数据点到其它某个数据点的距离小于该数据点到查询点的距离，就将该数据点的计数器的值减小1，直到当k的值为0时，说明这个数据点一定不是查询点的反k最近邻，把该点从候选集中删除。

在循环提纯算法中有四个输入参数，分别是查询点q，点检验集合Srp，节点检验集合Srr和候选集合S。输出参数是查询点q的反最近邻集SRKNN。循环提纯算法流程如图3所示。

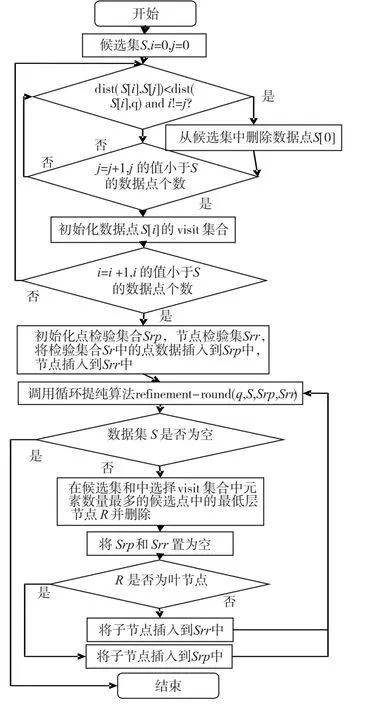
图3 提纯算法流程

提纯算法流程步骤如下：

［步骤1］从候选集合S中以次序选取一点p，直到S中所有的点都被选取出来过。如果所有的点都被取出来过，算法结束。

［步骤2］对于点检验集合Srp中的每一点 p′，都做以下操作：判断点p到点 p′的距离是否小于点p到点q的距离。如果点p到点 p′的距离小于点p到点q的距离。则将点p的计数器counter减小1，检验一下此时数据点p的计数器是否为0，如果为0，则说明p点是一个错误的命中，将p点从候选集合中删除，跳到步骤一继续执行。直到检验集合Srp中的所有数据点都判断一次后，继续执行步骤3。

［步骤3］对于节点检验集合Srr中的每一个节点R的最小矩形M，都做以下操作：判断点p到最小矩形M的最大距离是否小于点p到查询点q的距离，且R中数据点的数量是否大于点p的计数器counter的值。如果两个条件都成立的话，即p到最小矩形的最大距离小于点p到查询点q的矩形，并且R中包含的数据点的数量大于点p的计数器counter的值，说明p点是错误的命中，将p点从候选集合中删除，跳到步骤一继续执行。如果Srr中的每个节点都判断完毕后，继续执行步骤四。

［步骤4］对于节点检验集合Srr中的每一个节点的最小矩形M，都做以下操作：判断点p到最小矩形M的最小距离是否小于点p到查询点q的距离。如果小于的话，将节点加入到点p的Visit集合中，Visit集合是最后为了验证点点p是否是查询点q的反最近邻。

［步骤5］如果点p的Visit集合为空，p就是查询点q的反最近邻，将p从候选集合S中删除，加入到查询点q的反最近邻集合SRNN中。

反最近邻算法结合R树，空间裁剪方法，过滤数据过程与提纯算法过程实现，能够提高算法效率。

4 算法结果数据验证

采用两组数据来验证反最近邻查询算法实现结果。一组是自定义的数据，另一组是随机数据，根据两组数据的实现结果来验证反最近邻查询算法。采用表1简单数据点进行反最近邻查询结果说明。

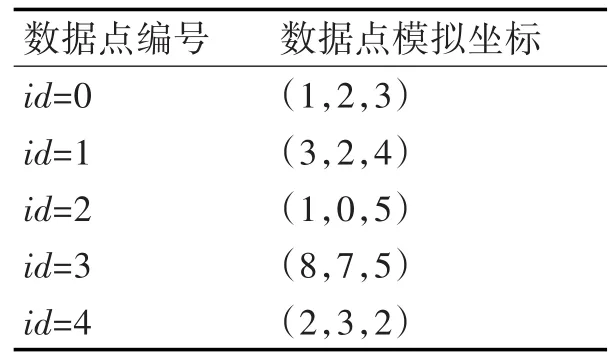
表1 简单实验数据

假设查询点的模拟坐标为（1，2，1），随着k取值的不同，反k最近邻查询的结果不同。将所用k的可能的取值所得到结果如表2所示。

表2 数据实验结果

若数据采用100个二维的随机数据点，由于数据点较多并且是随进产生的，所以不一一列出所有的随机数据点，而是给出二维数据点的位置模拟图4。

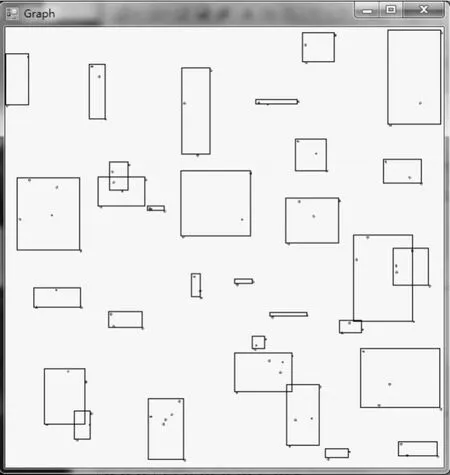
图4 二维数据点的位置模拟图

假设查询点的模拟坐标为（0，50），得到的查询点的反最近邻的结果如图5.3所示。查询点的反最近邻为id=56的数据点（24.32，32.32）和id=75的数据点（0.66，88.05），如图5所示。

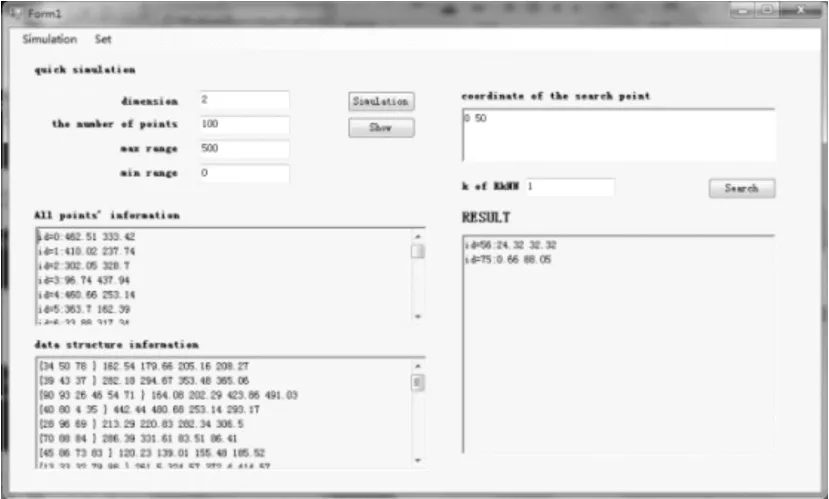
图5 随机点模拟实验结果

5 结语

目前，反最近邻查询技术已经广泛被应用到很多领域中。本文对反最近邻查询和反k最近邻查询的相关技术研究进行介绍并实现反最近邻算法中的多维空间裁剪算法，空间过滤算法，提纯算法。其优点在于支持任意k值的查询和多维空间的数据处理，能够保证反最近邻结果集中数据点的准确性，算法实现稳定性高，查询效率较好。

［1］ Nick Roussopoulos，Stephen Kelley，Frederic Vincent.Nearest neighbour queries［J］.Proceedings of the 1995 ACM SIGMOD international conference on Management of Date，1995：71-79.

［2］Sunil Aryan，David M.Mount，Nathan S.Netanyahu，Ruth Silverman，Angela Y.Wu.An optimal algorithm for approx⁃imate nearest neighbor searching fixed dimensions［J］.Journal of the ACM，1998：891-923

［3］PFlip Korn，PS.Muthukrishnan.Influence Sets Based on Reverse Neighbor Queries［J］.Proceedings of the 2000 ACM SIGMOD international conference on Management of data，2000：201-212.

［4］Congjun Yang，King-Ip Lin.An Index Structure for Effi⁃cient Reverse Nearest Neighbor Queries［J］.Proceedings of the 17th International Conference on Data Engineering，2001：485-492.

［5］PFlip Korn，PS.Muthukishnan，PDivesh Srivastava.Re⁃verse nearest neighbor aggregates over data streams［J］.Proceedings of the 28th international conference on Very Large Date Bases，2002：814-825.

［6］Rimantas Benetis，PS.Jensen，Gytis Karciauskas，Simonas Saltenis.Nearest and reverse nearest neighbor queries for moving objects［J］.Proceedings of the 2002 International Symposium on DatabaseEngineering&Applicationg，2002：44-53.

［7］Man Lung Yiu，Nikos Mamoulis.Reverse Nearest Netigh⁃bors Search in Ad-hoc Subspaces［C］//The 27th Interna⁃tional Conference on Data Engineering，2006：412-426.

［8］Yufei Tao，Dimitris Papadias，Xiang Lian，Xiaokui Xiao⁃nei.Multidimensional reverse kNN search［J］.The VLDB Journal，2007：293-316.

［9］Muhammad Aamir Cheema，Xuemin Lin，Ying Zhang，Wei Wang，Wenjie Zhang.Lazy updates：an efficient tech⁃nique to continuously monitoring reverse kNN［J］.Pro⁃ceedings of the VLDB Endowment，2009：1138-1149.

［10］邓红艳，武芳，翟仁健，等.一种用于空间数据多尺度表达的R树索引结构［J］.计算机学报，2009，32（1）：177-184.DENG Hongyan，WU fang，ZHAI Renjian，et al.R-Tree Index Structure for Multi-Scale Representation of Spatial Data［J］.Chinese journal of computers，2009，32（1）：177-184.