边坡形变Verhulst建模及后验差检验

杨豪 刘永来 徐瀚周

摘要：基于GNSS监测数据，采用Verhulst模型对水库边坡区域地表沉降与时间问题进行建模研究，并以后验差检验法对建模结果进行验证。结果表明，该模型计算简单，模型参数较少，预测精度较高，能够有效的表征边坡监测体的沉降变化规律。

Abstract： Based on the GNSS monitoring data， the Verhulst model is used to modeling the surface subsidence and the time problem in the slope area of the reservoir. The model test results are verified by the post-test difference method. The results show that the model is simple， the model parameters are less， the prediction accuracy is higher， which can effectively characterize the variation of slope monitoring body settlement.

关键词：Verhulst模型；边坡沉降；后验差检验

Key words： Verhulst model；slope settlement；posterior difference test

中图分类号：P258 文献标识码：A 文章编号：1006-4311（2018）12-0110-03

0 引言

随着自然灾害的频繁发生，变形监测与数据分析已成为工程实践的重要组成部分。在长期的斗争中，人们逐渐认识到监测只是基础，数据分析和预警才是关键[1，2]。滑坡作为重大的边坡事故，具有较大的破坏性[3]。因此，有必要对其受力过程和变形机理进行深入的分析，建立动态预测模型，合理、科学的作出预警。

纵观已有的研究成果，变形观测数据分析主要包括回归分析、灰色理论和时间序列等方法[4，5]。费尔哈斯（Verhulst）模型[6]作为灰色理论的一种特殊模型，是由德国生物学家Verhulst于1837年在研究生物繁殖规律时提出的[6]。主要用来描述具有饱和状态的过程，即S形过程。该过程与边坡沉降机理具有良好的对应关系。本文以此来研究水库边坡区域地表沉降与时间问题，以期能够有效地反映边坡监测体的沉降变化规律。

1 边坡形变Verhulst建模

1.1 粗差探测与数据插补

由于形变监测数据受监测设备、外界监测环境以及观测者主观因素的影响，外业获取的数据中很有可能存在粗差。因此需要对观测数据进行预处理。

变形粗差通常满足以下的条件[7]：

式中，et为监测值的残差，s为标准差，k为待定参数，可由所选择的统计判别准则和样本特征确定。本文采用格拉布斯准则进行粗差探测：

假设存在一组等精度独立观测序列：x1，x2，…，xn，其算术平均值为：

则观测序列的残差为：

则残差中误差为：

m= （4）

由式（4）可知：当et>km时，认为xt中含有粗差，应予以剔除，以保证后期数据处理的精度。k=λ（α，n），k的值可根据剔除水平α和样本数n查表求得，具体数值见相应规范。

在对含有粗差的形变监测序列进行粗差剔除后，为了不改变原始监测序列的完整性，有必要对剔除粗差后的序列进行数据插补。数据插补满足以下条件：

①当为单点粗差时，即xt为粗差，则相应的插补值为：

xt？坩 （5）

②当为双点粗差时，即xt，xt+1为粗差，则相应的插补值为：

xt？坩xt+1？坩 （6）

1.2 建模数据预处理

在对数据序列进行建模分析前，需要进行预处理，以保证数据的合理性。设序列为x（0）=（x（0）（1），x（0）（2），…，x（0）（n）），计算序列的级比为：

λ（k）=，（k=2，3，…，n） （7）

当所有的级比λ（k）都落入可容覆盖范围Θ=（e，e）内时，说明序列x（0）满足建立Verhulst模型的数据要求，则可进行拟合、预测。否則，需对序列进行变换处理，常用的变换方法有加常数的平移变换。

1.3 Verhulst建模原理

设x（0）为原始数据序列，有

x（0）=（x（0）（1），x（0）（2），…，x（0）（n）） （8）

x（1）为x（0）的一次累加生成（1-AGO）序列，有

x（1）=（x（1）（1），x（1）（2），…，x（1）（n）） （9）

z（1）为x（1）的均值生成序列，有

z（1）=（z（1）（2），z（1）（3），…，z（1）（n）） （10）

则称

x（0）+az（1）=b（z（1））2（11）

为Verhulst模型，a和b为参数。称

+ax（1）=b（x（1））2 （12）

为Verhulst模型的白化方程，其中t为时间。

设Verhulst模型如上所述，若

=[a，b]T （13）

为参数列，且

B=-z（1）（2） （z（1）（2））2-z（1）（3） （z（1）（3））2 -z（1）（n） （z（1）（n））2，Y=x（0）（2）x（0）（3） x（0）（n） （14）

则参数列的最小二乘估计满足

=[，]T=（BTB）-1BTY （15）

设Verhulst模型如上所述，则白化方程的解为

x（1）t= （16）

灰色Verhulst模型的时间响应序列为

（1）（k+1）= （17）

累减还原式为

（0）（k+1）=（1）（k+1）-（1）（k）（18）

2 后验差检验

为了验证Verhulst模型的有效性，应用后验差检验法[8]对模型拟合结果进行分析。设t时刻的边坡形变观测值为x（0）（t），模型的拟合值为（0）（t），x为原始序列的平均值，即x=x（0）（t），e（t）为观测值与拟合值之差，也称为t时刻的残差，即e（t）=x（0）（t）-（0）（t），e为其平均值，即e=e（t）。原始数据的均方差为S1=，残差均方差为S2=，则后验差比值C定义为：

C= （19）

小误差概率定义为：

p=P{e（t）-<0.6745S1} （20）

C和p作为评价Verhulst模型拟合性能好坏的两个指标，按p、C的大小，一般可将拟合精度分为4类，见表1。

3 Verhulst建模及后验差检验流程

采用流程图的形式表示Verhulst模型的计算过程如图1所示。

4 算例与分析

以阿海水电站库区边坡某监测点的GNSS沉降监测数据为例（表2）。采用Verhulst模型对数据进行建模研究，以1-10期为拟合区间，11-12期为预测区间，计算结果见表2。

根据表2数据，绘制预测曲线如图2所示。

以后验差检验法对模型拟合能力进行验证，相关指标数值及所对应的精度等级见表3。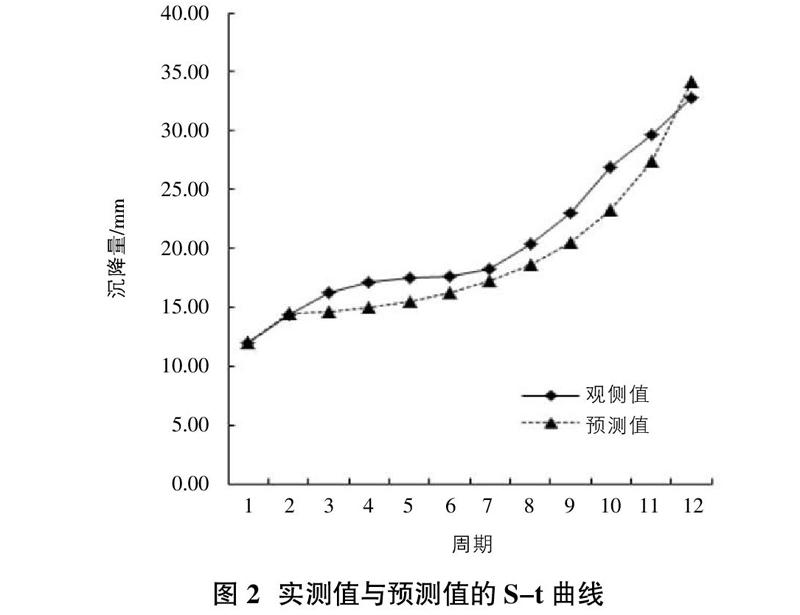

后验差验证结果表明，Verhulst模型能够有效地表征水库边坡区域地表沉降与时间的关系问题，且具有较好的拟合、预测能力。

5 结论

研究结果表明，Verhulst模型能够较好地表征水库边坡的沉降变化情况。这主要是由于模型本身所描述的系统发展规律与水库边坡沉降的发生过程具有内在的一致性。因此，在实际工程中，可以依据GNSS监测水库边坡的沉降观测资料，利用Verhulst模型来预测其不同时刻的沉降量。由于Verhulst模型要求的观测数据不多，且计算较为简单，因此，值得在实际工程中验证与运用。

参考文献：

[1]杨建文.变形预测组合模型建模方法研究与精度分析[D].昆明：昆明理工大学，2014.

[2]候建国，王腾军.变形监测理論与应用[M].北京：测绘出版社，2008.

[3]张奇华，丁秀丽，邬爱清.滑坡变形预测与失稳预报问题的几点讨论[J].中国地质灾害与防治学报，2005（2）：1-7.

[4]黄声享，尹晖，蒋征.变形监测数据处理[M].二版.武汉：武汉大学出版社，2010.

[5]伊晓东，李宝平.变形监测技术及应用[M].郑州：黄河水利出版社，2007.

[6]王利红，罗明奇.Verhulst模型的改进研究[J].数学的实践与认识，2012，42（8）：113-116.

[7]刘强.测量数据处理中粗差问题的探讨[J].科技情报开发与经济，2011（5）：218-219.

[8]李红霞，赵新华，迟海燕，等.基于改进BP神经网络模型的地面沉降预测及分析[J].天津大学学报，2009，42（1）：60-64.