以质心为速度参考点的恢复系数的定义及应用

宋辉武

(鄂尔多斯市第一中学，内蒙古 鄂尔多斯 017010)

1 以质心为速度参考点的恢复系数的定义

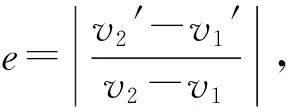
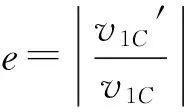
对于撞击球1来说,有

(1)

对于被撞球2来说,有

(2)

其中vC为质心的速度,即碰撞的压缩阶段刚刚结束，即将进入恢复阶段时两体共速时的那个速度,满足m1v1+m2v2=(m1+m2)vC,当然为了方便初学者理解与记忆,式中的vC也可以写作v共．

实际上,我们可以根据牛顿恢复系数推导得出以质心为速度参考点的恢复系数,对于一个两体碰撞过程来说,当系统满足动量守恒定律时,有

m1v1+m2v2=m1v1′+m2v2′，

进而可得

(3)

(4)

有趣的是如果我们对(3)、(4)两式进行巧妙地变形即可得到(1)、(2)两式.

对于(3)式来说,

vC-e(v1-vC).

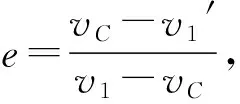
对于(4)式来说,

vC+e(vC-v2)

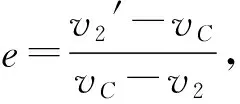
不难发现,按照这种定义方式,如果我们已知碰撞前两个球各自的速度,则根据(1)、(2)两式可以简捷、准确地直接写出碰后两个球的速度分别为多大,不需要列方程组进行繁琐地求解．而事实上,以质心为速度参考点的恢复系数其用武之地远不止这些,为了进一步说明其应用价值,下面再来尝试处理几例典型的两体对心碰撞中的疑难问题．

2 以质心为速度参考点的恢复系数的应用

例1.甲、乙两名滑冰运动员在光滑的冰面上沿同一直线相向运动,速度的大小分别为v甲、v乙,且v甲=3 m/s,v乙=1m/s,迎面碰撞后(正碰)甲、乙两人均反向运动,速度大小均为vt=2m/s,则甲、乙两人的质量之比为

(A) 2∶3. (B) 2∶5.

(C) 3∶5. (D) 5∶3.

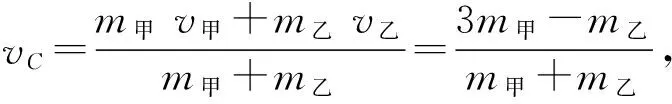
解得

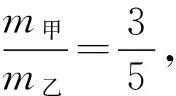
例2.在光滑水平面上,A、B两球沿同一直线同向运动,碰撞后粘在一起,若碰撞前A、B两球的动量分别为6 kg·m/s、14 kg·m/s,碰撞中B球动量减少6 kg·m/s,则A、B两球碰撞前的速度之比为

(A) 3∶7. (B) 3∶4.

(C) 2∶7. (D) 7∶4.

解析:由于碰撞后粘在一起,因此恢复系数e=0,由题可知,质心的速度为

vC-v1′=0,

现在我们只需要考察撞击球,而B为撞击球,且碰后B球的动量为8 kg·m/s,根据vC-vB′=0,有

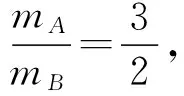
例3.动量分别为5 kg·m/s和6 kg·m/s的小球A、B沿光滑水平面上的同一条直线同向运动,A追上B并发生碰撞后,若已知碰撞后A的动量减小了2 kg·m/s,而方向不变,则A、B质量之比可能是

(A) 5∶6. (B) 3∶8.

(C) 1∶2. (D) 4∶7.

解析:由题可知,碰撞后A的动量为3 kg·m/s,且质心的速度为

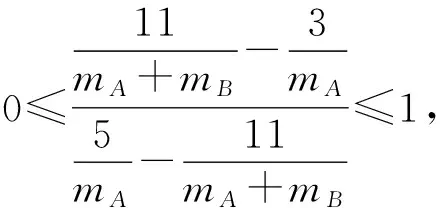
选项(B)、(C)、(D)正确．

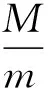
(A) 2. (B) 3. (C) 4. (D) 5.

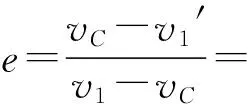
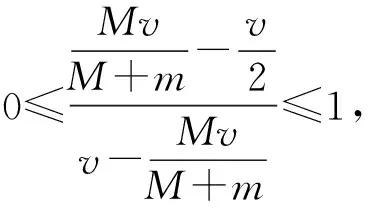
3 结语

可以看出以质心为速度参考点的恢复系数不仅形式上具有很强的简洁性、对称性,而且针对很多实际问题与传统的牛顿恢复系数一样具有很好的应用价值,笔者查阅了相关的大中学教材以及相关文献,发现目前还没有此种定义方式,鉴于此,笔者撰写本文,希望可以抛砖引玉,引起广大的大中学物理教师的重视并进一步挖掘其使用价值,进而能更好地服务于物理教学,促进基础教育的进步与发展．

参考文献：

1 李逸良,邱信明,张雄.恢复系数的不同定义及其适用性分析[J].力学与实践,2015(06):773-777.

2 漆安慎,杜婵英.力学[M].北京:高等教育出版社,2005:138-145.

3 赵凯华,罗蔚茵.新概念物理教材.力学[M].北京:高等教育出版社,2004:128-131.

4 陈长.恢复系数在一维碰撞中的巧妙运用[J].物理教师,2017(9):91-92.