利用非惯性参考系求解高中物理典型习题初探

刘安巍

(哈尔滨师范大学教师教育学院,黑龙江 哈尔滨 150025)

利用惯性参考系求解高中物理习题是广泛认可的基本思路．对于部分典型习题,如相对运动求解位移、时间、加速度等,若选用非惯性参考系求其解较选用惯性参考系方便且高效．

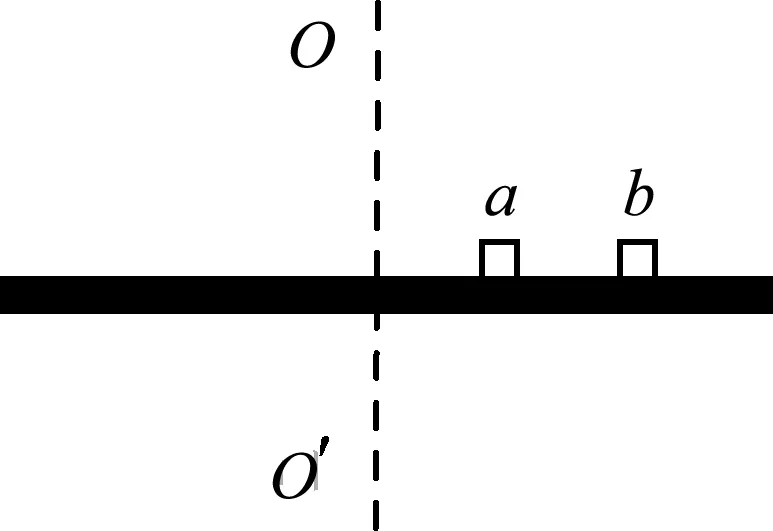
图1

例1.如图1所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l．木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是

(A)b一定比a先开始滑动.

(B)a、b所受的摩擦力始终相等.

本题是高中阶段常见的类型题,在求这一类题的过程中,通常以摩擦力提供向心力来进行求解．如果将圆盘当做参考系,转动的圆盘就是一个非惯性系．用非惯性系来看待问题,所列的式子跟摩擦力提供向心力完全一样．

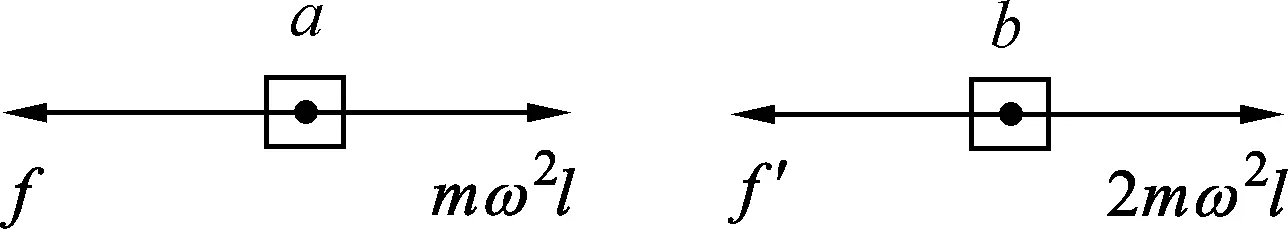
图2

解析:以圆盘作为非惯性参考系,补充分析离心惯性力后,如图2分别对a和b进行受力分析得最大静摩擦力方程为

fm=kmg，

对物体a受力分析得

f=mω2l，

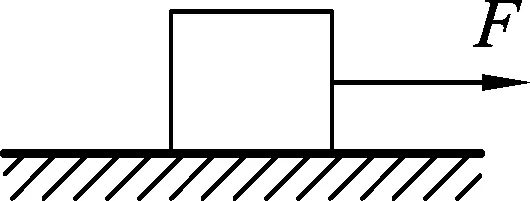
图3

对b物块进行受力分析得

f′=2mω2l．

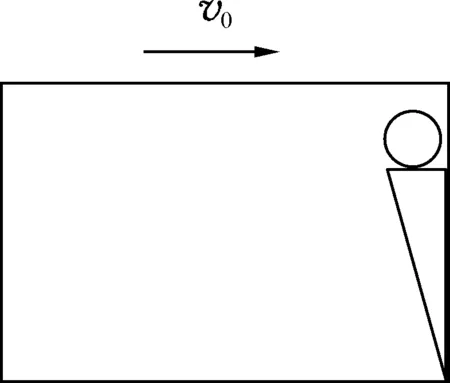
图3

例2.如图3所示,匀速行驶的小车内,高为h的货架上放有一小球,小车突然以加速度a匀加速运动．求:小球落地点到货价下端的距离s．(小球可视为质点,货价可视为与小车一样高)

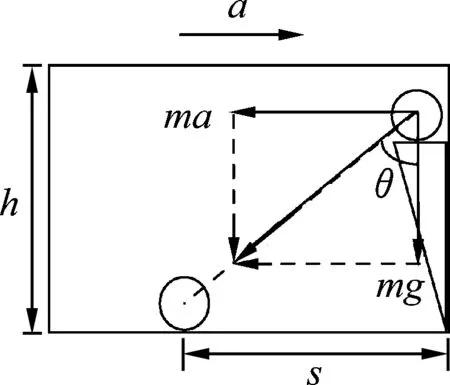
图4

解析: 以匀加速运动的小车为参考系,则小球将做以初速度为0的匀加速直线运动,如图4所示．

(1)

(2)

由(1)、(2)式得

评析:若以地面为惯性参考系进行求解,必须通过位移关联列出方程进而计算出最终结果．小球落点位置距货架低端距离s=s车-s球,通过时间相关性得出水平方向位移关系,进而得出最后结果．若以小车为非惯性参考系进行求解,不需要考虑球跟车的位移关系,只需要分析清楚球的受力情况和运动状态即可,最后用三角形边角关系直接求得结果．

图5

例3.如图5所示,质量为m2的三角形木块,倾角为θ,放在光滑水平面上,另一质量为m1的木块放在三角形顶端自由下滑．如果接触面的摩擦可以忽略不计,求m2物块的加速度.

图6

解析:以m2物块为非惯性参考系受力分析如图6所示，设小物块沿斜面向下的加速度为am1(沿斜面向下),大物块水平方向的加速度为am2．

对大物块进行受力分析得

(1)

则小物块具有向左的惯性力F为

(2)

则小物块沿斜面向下的合力为

F合=Fcosθ+m1gsinθ=m1am1.

(3)

FN+Fsinθ=m1gsinθ.

(4)

可得

(5)

由(1)、(3)、(5)式得

m2竖直方向的加速度为0．

评析:若以地面为惯性参考系进行求解,则必须对m1和m2分别进行受力分析,然后根据水平方向竖直方向的位移关系进行列方程求解,过程极为复杂繁复．若以m2为非惯性参考系进行求解,会避免复杂的几何关系,直接对小物块进行受力分析,列牛顿第二定律方程算出各自的加速度．本题还能以m1为非惯性参考系进行求解,但是以3个不同的参考系进行对比来说,以地面为参考系最为复杂,以m2为参考系进行问题处理最为简单．由此可见,对此类习题运用非惯性参考系解题更有利于问题的解决．

参考文献：

1 张三慧.大学物理(第1册)力学[M].北京:清华大学出版社,1999:84.

2 陈晓宇.巧用平动惯性系解决高中物理力学问题[J].物理通报,2013(7):108-109.

3 王永柱.力学问题的惯性系和非惯性系解法对比[J].高教学刊,2016(21):138-139.

4 马文蔚,周雨青.物理学教程(第2版)上册[M].北京:高等教育出版社,2006:33-34.

5 李莉.非惯性系动力学在中学物理问题中的分析讨论[J].湖南中学物理,2017(5):21-24.