一类分数阶微分方程耦合系统边值问题解的存在性

薛益民，苏有慧，刘 洁，苏 莹

(徐州工程学院 数学与物理科学学院,江苏 徐州 221018)

分数阶微分方程具有深刻的物理背景和丰富的理论内涵，与整数阶微分方程相比，分数阶微分方程在描述自然、物理、化学等诸多现象时更具准确性，因此，分数阶微分方程边值问题的研究，对解决现实生活中的非线性问题具有重要意义.几十年以来，分数阶微分方程发展迅速，逐渐成为非线性分析的重要的分支之一，受到越来越多研究者关注[1-5]，同时，对分数阶微分方程耦合系统的研究也日益得到重视，其在热力学、流体力学、生物科学、扩散过程等科学领域正在被广泛应用[6-9].

文献[10]研究了下面Riemann-Liouville型分数阶微分方程

借助于锥上的不动点定理，获得了正解的存在性以及多重性结果，其中1<α≤2.

文献[11]研究了如下Riemann-Liouville型分数阶微分方程

利用锥拉伸与压缩不动点定理，给出了上述方程正解的存在性定理，其中2<α≤3，λ>0.

文献[12]研究了下列Riemann-Liouville型分数阶微分方程

运用锥上的不动点定理与Leray-Schauder非线性抉择理论等方法，给出了上述方程正解的存在性、多重性和唯一性的充分条件，其中3<α≤4.

受文献[10-12]启发，将研究下列非线性分数阶微分方程耦合系统边值问题

(1)

解的存在性，其中α<2,β≤3,1<γ,δ≤2,1+γ≤α,1+δ≤β,f,g∈C([0,1]×[0,∞),[0,∞)),Dλ表示λ阶Riemann-Liouville分数阶导数，λ∈{α,β,γ,δ}.借助格林函数的性质和Guo-Krasnosel'skii's不动点定理，得到该耦合系统解的存在性结果.

1 预备知识

为研究需要，本节给出Riemann-Liouville型分数积分等定义以及相关结果，详见[13-18].

定义1[13]函数f:R+→R的α>0阶Riemann-Liouville积分为

其中右边在R+上逐点定义.

定义2[13,14]函数f:R+→R的α>0阶Riemann-Liouville导数为

其中n=[α]+1,[α]表示实数α的整数部分，右边在R+上逐点定义.

引理2[13]若α,β>0,f(t)∈L(0,1)，则有

1)DβIαf(t)=Iα-βf(t),α>β；

2)DαIαf(t)=f(t)；

下面介绍本文的主要工具.

1) ‖Ax‖≤‖x‖,∀x∈P∩∂Ω1且‖Ax‖≥‖x‖,∀x∈P∩∂Ω2；

2) ‖Ax‖≥‖x‖,∀x∈P∩∂Ω1且‖Ax‖≤‖x‖,∀x∈P∩∂Ω2.

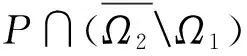
引理4对于∀y(t)∈C[0,1],2<α≤3,1<γ≤2,1+γ≤α分数阶微分方程边值问题

(2)

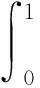
(3)

证明 由引理2的3)，方程(2)等价于积分方程

(4)

由u(0)=0，可得c3=0.由引理2的1)和2)，可得

由Dγu(0)=Dγu(1)=0，有

将c1,c2,c3代入(4)，有

类似可得

引理5假设G(t,s)=(Gα(t,s),Gβ(t,s))，则G(t,s)满足：

1) 对∀t,s∈[0,1]，有G(t,s)∈C([0,1]×[0,1])；

2) 对∀t,s∈[0,1]，有G(t,s)≥0，且对∀t,s∈(0,1)，有G(t,s)>0；

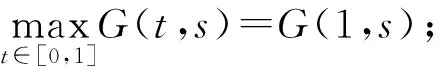
证明：为叙述方便，在Ga(t,s),的表达式中，记

由G(t,s)的表达式，易知1)和2)成立.下面主要证明3)和4).

3) 由2<α≤3,1<γ≤2,1+γ≤α，有

因此，Gα(t,s)关于t是单调增函数.类似可得，Gβ(t,s)关于t也是单调增函数，故3)成立.

4) 由3)，对于2<α≤3,1<γ≤2,1+γ≤α,s∈[0,1]，有

因此

类似可得

故4)成立.

2 主要结论

本节将借助格林函数的性质和Guo-Krasnosel'skii's不动点定理，研究耦合系统(1)解的存在性.

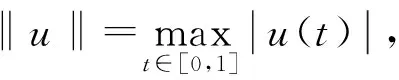
U={(u(t),v(t))∈X×Y:u(t)≥0,v(t)≥0,t∈[0,1]}.

定义锥V⊂X×Y为

其中μα和μβ由引理5的(4)给出.对∀(u,v)∈X×Y，定义算子T:X×Y→X×Y为

(5)

由引理4知T的不动点即为耦合系统(1)的解.

引理6设f,g∈C([0,1]×[0,∞),[0,∞))，则算子T:U→U和T:V→V是全连续的.

证明： 对∀(u,v)∈U，由f,g和G(t,s)的非负性，知T(u,v)(t)≥0，因此，T(U)⊆U，即T:U→U.首先，证明算子T:U→U一致有界.对∀(u,v)∈U，由f,g和G(t,s)的连续性，知算子T是连续的.令

Ω={(u(t),v(t))|(u,v)∈U,‖(u(t),v(t))‖≤R,R>0,t∈[0,1]}，

则Ω是U的一个非空有界闭子集.由f,g的连续性，知对∀(u,v)∈Ω,t∈[0,1]，存在K1,K2>0，使得f(t,v(t))≤K1，g(t,u(t))≤K2.

由Gα(t,s),Gβ(t,s)的非负性，有

和

其次，证明算子T:U→U等度连续.对∀t,s∈[0,1]，由引理5的1)，知Gα(t,s)是连续的，从而Gα(t,s)在[0,1]×[0,1]上一致连续.因此，对固定的s∈[0,1]和任意的t∈[0,1]，存在δ>0，当t1,t2∈[0,1]且|t2-t1|<δ时，有|Gα(t2,s)-Gα(t1,s)|<ε/(2K1).

所以

(6)

类似可得

(7)

由(6)、(7)，可得

‖T(u,v)(t2)-T(u,v)(t1)‖<ε,

因此，算子T:U→U是等度连续的.依据Arzela-Ascoli定理，可知算子T:U→U是全连续的.

下面证明T(V)⊆V.对∀(u,v)∈U，根据U和T的定义，可得T(U)∈U.由引理5的4)，对∀t∈[1/2,1]，有

(8)

由引理6，有

(9)

由(8)、(9)，可得

Tαv(t)≥μα‖Tαv‖,∀t∈[1/2,1],

类似可得

Tβu(t)≥μβ‖Tβu‖,∀t∈[1/2,1].

因此T(u,v)∈V，即T(V)⊆V.接下来，类似T:U→U的证明过程，即得T:V→V是全连续的.

为叙述方便，记

定理1设f,g∈C([0,1]×[0,∞),[0,∞))，若下面条件成立：

(H1)存在常数a1,a2>0且min{a1,a2}≥1满足

a1Lα

(H2)存在常数b1,b2>0且b1+b2≤1满足

0≤f∞

则耦合系统(1)至少有一个解.

证明由(H1)，可选择充分小的正常数ε1和ε2满足

0<ε1

因此，存在常数r>0满足

f(t,v)≥(f0+-ε1)v,(t,v)∈[0,1]×[0,r]

(10)

和

g(t,u)≥(g0+-ε2)u,(t,u)∈[0,1]×[0,r],

令

Ωr={(u,v):(u,v)∈X×Y,‖(u,v)‖

由V的定义，设(u,v)∈V∩∂Ωr，对∀s∈[1/2,1]，有

(11)

设t∈[1/2,1]，由(H1)、(10)、(11)和引理5的4)，对∀(u,v)∈V∩∂Ωr，有

类似可得

‖Tβu(t)‖≥a2‖u‖,

因此

‖T(u,v)‖ =‖Tαv(t)‖+‖Tβu(t)‖≥a1‖v‖+a2‖u‖≥min{a1,a2}(‖v‖+‖u‖)

=min{a1,a2}‖(u,v)‖≥‖(u,v)‖,

即

‖T(u,v)‖≥‖(u,v)‖，∀(u,v)∈V∩∂Ωr.

另一方面，由(H2)，可选择充分小的正常数ε3和ε4满足

0<ε3

因此，存在常数R>0满足

f(t,v)≤(f∞+ε3)v,(t,v)∈[0,1]×(R,∞)

(12)

和

g(t,u)≤(g∞+ε4)u,(t,u)∈[0,1]×(R,∞).

(13)

由f,g∈C([0,1]×[0,∞),[0,∞))，可知存在非负常数Nα,Nβ,使得

(14)

由(12)、(13)和(14)，可得

f(t,v)≤(f∞+ε3)v+Nα,(t,v)∈[0,1]×[0,∞)

和

g(t,u)≤(g∞+ε4)u+Nβ,(t,u)∈[0,1]×[0,∞).

令

ΩR*={(u,v):(u,v)∈X×Y,‖(u,v)‖

其中

(15)

设(u,v)∈V∩∂ΩR*,t∈[0,1]，由引理5的3)和(15)，有

因此

‖Tαv(t)‖≤b1‖(u,v)‖,(u,v)∈V∩∂ΩR*,

类似可得

‖Tβv(t)‖≤b2‖(u,v)‖,(u,v)∈V∩∂ΩR*,

所以

‖T(u,v)‖ =‖Tαv(t)‖+‖Tβu(t)‖≤b1‖(u,v)‖+b2‖(u,v)‖

=(b1+b2)‖(u,v)‖≤‖(u,v)‖,

即

‖T(u,v)‖≤‖(u,v)‖，(u,v)∈V∩∂ΩR*.

参考文献：

[1] SUN Y，ZHAO M.Positive solutions for a class of fractional differential equations with integral boundary conditions[J].Applied Mathematics Letters，2014，34：17-21.

[2] ZHANG X，WANG L，SUN Q.Existence of positive solutions for a class of nonlinear fractional differential equations with integral boundary conditions and a parameter[J].Applied Mathematics and Computation，2014，226：708-718.

[3] CHEN T，LIU W，HU Z.A boundary value problem for fractional differential equation with P-Laplacian operator at resonance[J].Nonlinear Analysis，2012，75(6)：3210-3217.

[4] GOODRICH S.On a fractional boundary value problem with fractional boundary conditions[J].Applied Mathematics Letters，2012，25(8)：1101-1105.

[5] GRAEF R，KONG L.Positive solutions for a class of higher order boundary value problems with fractional Q-Derivatives [J].Applied Mathematics and Computation，2012，218(19)：9682-9689.

[6] SHAH K,KHAN R A.Existence and uniqueness of positive solutions to a coupled system of nonlinear fractional order differential equations with Anti-Periodic boundary conditions [J].Differ Equ Appl，2015，7(2)：245-262.

[7] JIANG W.Solvability for a coupled system of fractional differential equations with integral boundary conditions at resonance[J].Advances in Differential Equations，2013，324：1-13.

[8] AHMAD B，NTOUYAS S K.A fully hadamard type integral boundary value problem of a coupled system of fractional differential equations[J].Fractional Calculus and Applied Analysis，2014，17(2)：348-360.

[9] SHAH K,KHALIL H，KHAN R A.Upper and lower solutions to a coupled system of nonlinear fractional differential equations[J].Prog Fract Differ Appl，2016，2(1)：1-10.

[10] BAI Z，LU H.Positive solutions for boundary value problem of nonlinear fractional differential equation [J].J Math Anal Appl，2005，311(2)：495-505.

[11] WANG Y，LIU L，WU Y.Positive solutions for a class of fractional boundary value problem with changing sign nonlinearity [J].Nonlinear Analysis，2011，74(17)：6434-6441.

[12] XU X J，JIANG D Q，YUAN C J.Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation[J].Nonlinear Analysis，2009，71：4676-4688.

[13] KILBAS A A，SRIVASTAVA H M，TRUJILLO J J.Theory and applications of fractional differential equations[M].Elsevier，Amsterdam，2006.

[14] PODIUBNY I.Fractional differential equations[M].Academic Press，San Diego，1999.

[15] GUO D,LAKSHMIKANTHAM V.Nonlinear problems in abstract cones[M].Academic press，San Diego，1988.

[16] JLELI M,SAMET B.Existence of positive solutions to a coupled system of fractional differential equations[J].Mathematical Methods in the Applied Sciences，2015，38(6)：1014-1031.

[17] 薛益民，苏莹，苏有慧.一类含积分边界条件分数阶微分方程解的存在性和唯一性[J].安徽师范大学学报(自然科学版)，2017，40(4)：312-317.

[18] 薛益民.非线性Caputo型分数阶微分方程耦合系统边值问题解的存在性[J].河北师范大学学报(自然科学版)，2017，41 (3)：200-207.