基于ARMA模型的滚动轴承故障诊断研究

韩清鹏，李天成，李晨晨，朱 瑞，张梅琳

0 引言

滚动轴承是旋转机械中应用最广泛的承载和传动部件，存在着大量的多发故障，其缺陷会导致生产中断，造成巨大的经济损失，甚至带来灾难性的后果。因此，准确诊断其故障及稳定性是不可忽视的重要问题[1-3]。

故障诊断以故障模式识别为基础，特征提取最为关键。在故障特征提取中，传统方法大都以信号的时域和频域特征为基础，建立各类判别函数来诊断系统的工作状态。但是，由于滚动轴承工况复杂，有时很难仅通过时域或频谱分析来对滚动轴承的真实状态做出较为准确的评定。时间序列模型是一个信息的凝聚器[4-6]，可将系统特性与系统工作状态的所有信息都凝聚于其中，因而可依据它对滚动轴承的状态进行诊断。

基于滚动轴承振动信号峭度值的轴承故障特征提取方法，可实现故障冲击成分的提取和分析[7]。参数化ARMA模型能准确地描述动态系统的客观规律，其自回归参数对工况的变化规律反映最敏感。因此，采用基于滚动轴承振动信号峭度值ARMA模型的自回归参数作为特征向量来分析轴承的状态变化是十分有效的[8-10]。

本文首先给出了轴承故障预测模型参数的标定和调整方法；最后，对基于滚动轴承振动信号峭度值ARMA模型的轴承偏载条件下保持架断裂故障诊断进行了效果验证。

1 基于ARMA模型的滚动轴承故障预测算法

ARMA模型是用于状态观测的单变量时间序列模型，具有较强的状态描述能力和预测能力。基于ARMA模型的故障预测原理如图1所示，横轴为轴承工作时间t，纵轴为特征参数x(t)。

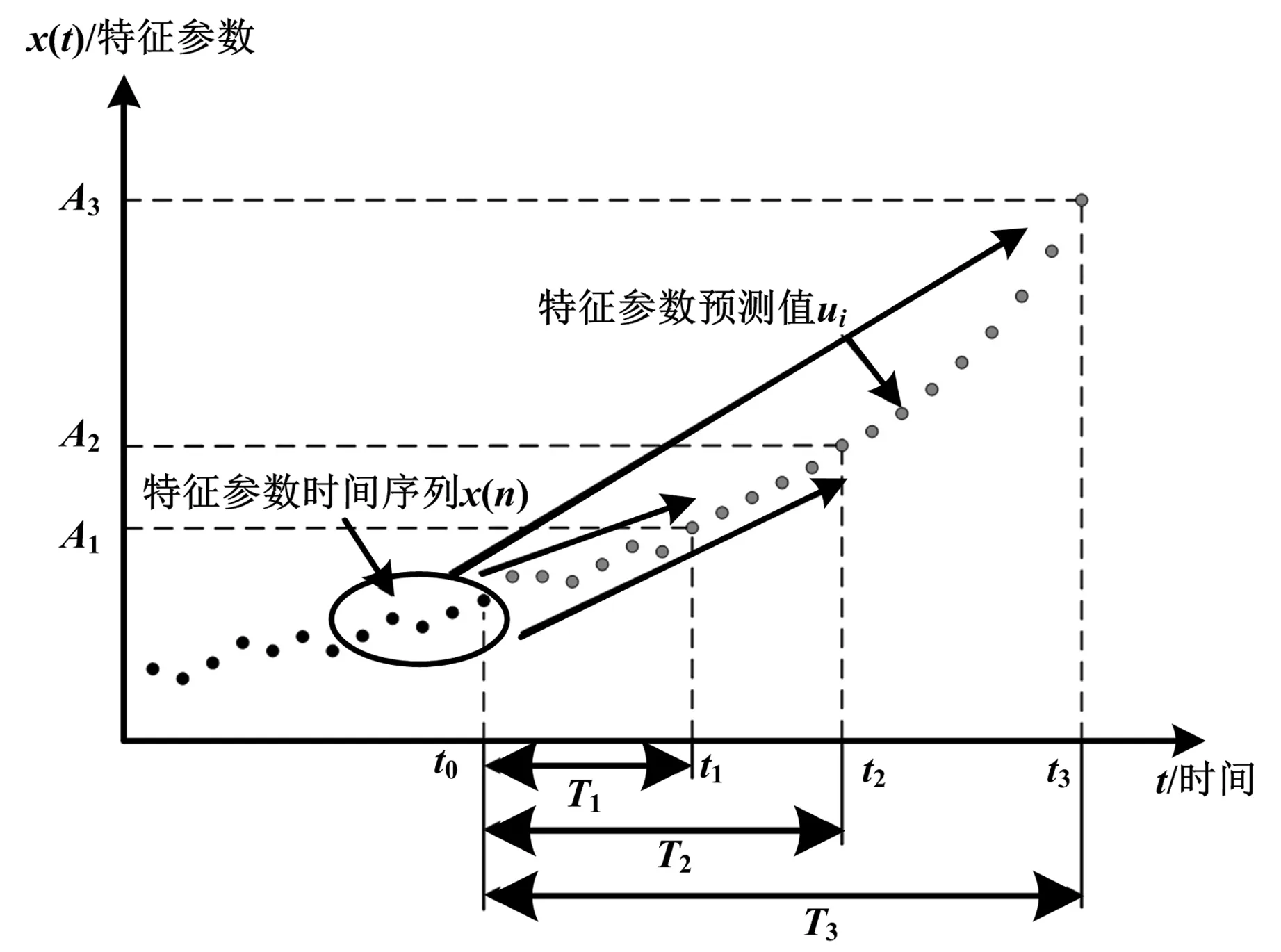
图1 基于ARMA模型的故障预测原理图Fig.1.Schematic diagramof fault prediction based on ARMA model

在建立ARMA模型预测轴承典型故障时，定义如下故障预测的参数：x(n)为利用特征参数x(t)建立的时间序列，其时间间隔为Δt；ui为利用ARMA模型计算得到的ti时刻特征参数预测值，ti=t0+Δt×i；特征参数值A1、A2、A3分别表示滚动轴承发生异常、故障、失效判定的特征参数阈值，是由故障诊断的经验值并综合考虑影响轴承故障发生发展和寿命等多种因素确定；t0为进行故障预测的起始时刻；t1、t2、t3分别表示滚动轴承发生异常、故障、失效的时刻；T1、T2、T3分别表示滚动轴承由起始时刻t0到发生异常、故障、失效的时间。利用基于ARMA模型的故障预测算法进行轴承故障预测包含以下步骤：

（1）利用当前时刻t0前时长为T0的一维特征参数数据，建立时间间隔为Δt的特征参数时间序列x(n)；

（2）利用时间序列x(n)进行模型识别与参数标定，获得ARMA模型的阶次、自回归参数和滑动平均参数；利用模型阶次和参数，建立考虑白噪声的ARMA模型；

（3）根据所建立的ARMA模型，利用振动实测数据的峭度值对模型的状态表征能力进行评价；

（4）基于所建立的ARMA模型，对t0时刻后续的特征参数进行预测，预测特征参数在各ti时刻的值ui，并与给定的判定阈值A1、A2进行对比；轴承发生故障、失效的判定条件分别是ui＞A1、ui＞A2，从而获得轴承达到故障、失效状态的时间T1、T2，以及相应地轴承发生故障、失效的时刻t1、t2（t1,2=t0+T1,2）；

（5）根据置信度、预测与实际的特征参数演化趋势，分别从预测精度和偏离程度两方面对预测结果进行评价。

具体实施基于ARMA模型的轴承故障预测时，需要完成以下计算：

取当前时刻t0以前的n个描述轴承状态的特征参数值x(t)，t0=Δt×n，Δt为时间间隔，按由0到Δt×n的时间先后顺序建立长度为n的时间序列x(n)：

进行ARMA模型识别，利用约束条件，比较不同阶次模型与序列的拟合程度，确定模型阶次p和q；利用当前时间序列x(n)对模型进行辨识，获得模型的自回归参数(φ1,φ2,…φp)与滑动平均参数(θ1,θ2,…θq)；根据所获得的阶次p和 q、自回归参数 (φ1,φ2,…φp)以及滑动平均参数 (θ1,θ2,…θq)，建立一个考虑白噪声 μn（满足均值为0、方差为的正态分布）的ARMA模型：

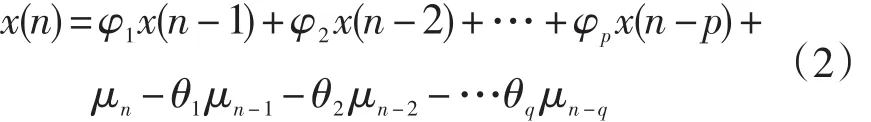
评价ARMA模型对数据的表征能力。引入实测数据，滑动选取不同时段的等时长特征参数，分别建立ARMA模型，利用compare函数计算两个ARMA模型的拟合度fit：

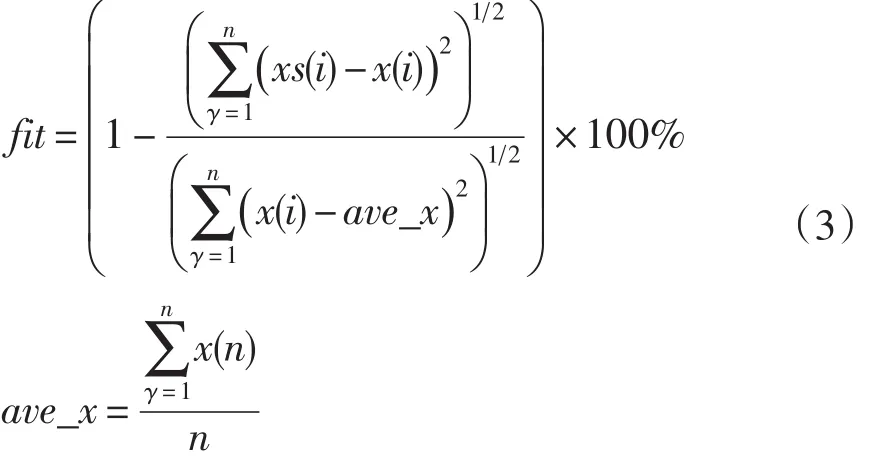
式（3）中，xs(i)为利用ARMA模型得到的序列。

利用所建立的ARMA模型，预测未来时刻ti=t0+Δt×i的特征参数ui（利用Δt内的轴承振动数据计算得到的特征参数），i=1,2,…,nmax。

2 滚动轴承监测及故障诊断实验系统

滚动轴承转子试验台的实测振动分析，搭建的试验台采用卧式转子结构，由驱动电机带动，主体结构形式如图2所示。

开展偏载条件下保持架断裂的滚动轴承加速寿命试验，获得振动信号测试信号数据，分析其振动故障特征。滚动轴承试验系统选取了角接触球轴承，振动信号的采集频率为4 kHz，本文选取轴承转速为240 r/min。

图2 滚动轴承转子试验台结构图Fig.2.The rotor supported on the rolling bearings test-platform

3 滚动轴承监测及故障诊断结果与分析

所测偏载条件下保持架断裂的滚动轴承的振动信号如图3所示。峭度值具有与波峰因素类似的变化趋势。峭度指标的绝对值越大，说明轴承偏离其正常状态，故障越严重。偏载条件下保持架断裂的滚动轴承振动信号峭度值K，如图4所示。

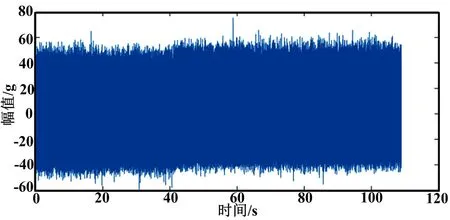
图3 偏载条件下保持架断裂的滚动轴承振动信号Fig.3.Vibration signals of cage fracture under partial load condition of therollingbearings

图4 偏载条件下保持架断裂的滚动轴承振动信号峭度值Fig.4.Kurtosis of the vibration signals of cage fracture under partial load condition of the rolling bearings

滑动平均后的轴承振动信号峭度值如图5所示。

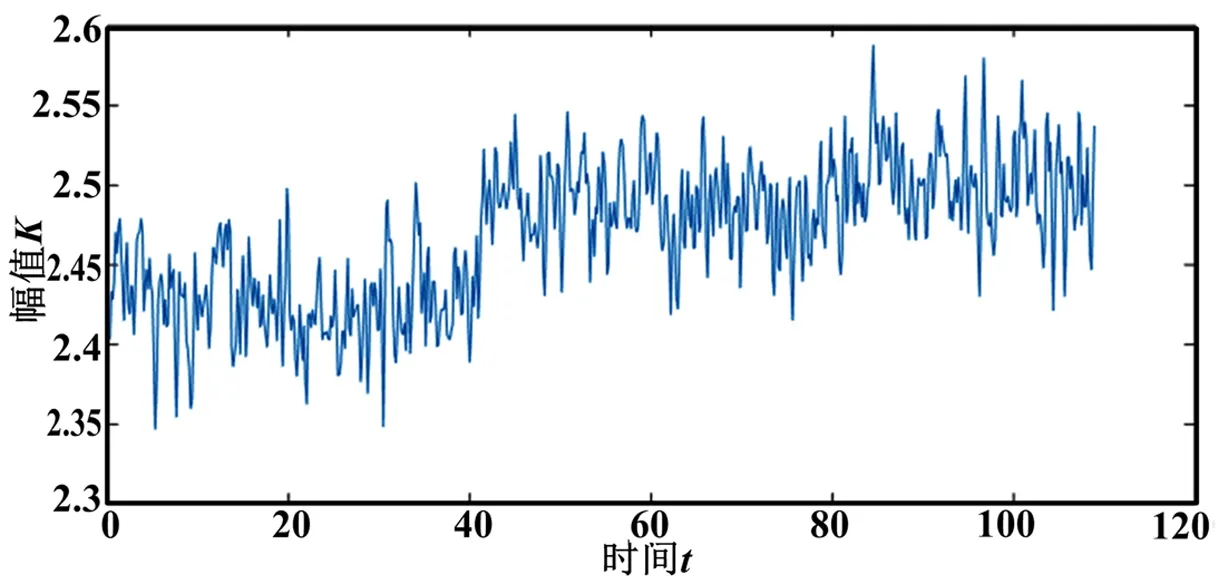
图5 平滑后的偏载条件下保持架断裂的滚动轴承振动信号峭度值Fig.5.Kurtosis of the vibration signals after smoothing of the cage fracture under partial load condition of the roll⁃ingbearings

从t0=15开始，截取一段时长为10 s的轴承振动信号峭度K序列用于ARMA建模，如图6所示。

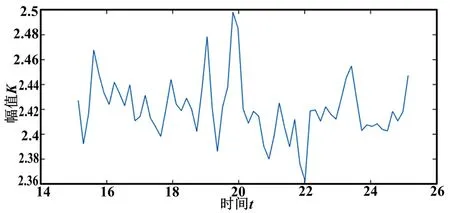
图6 10秒钟偏载条件下保持架断裂的滚动轴承振动信号峭度Fig.6.Kurtosis of the vibration signals of cage fracture under partial load condition experiment of the rolling bear⁃ings(10seconds)

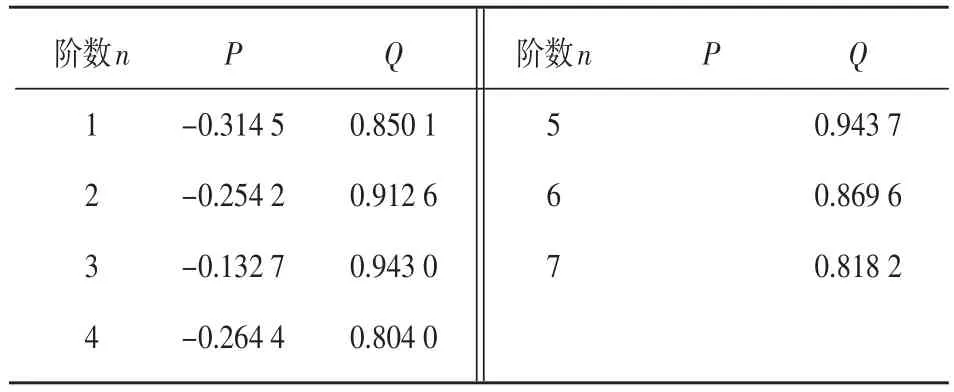
表1 偏载条件下保持架断裂的滚动轴承振动信号ARMA模型参数Table.1.ARMA parameters of the Kurtosis of thevibration signals of cage fracture under partial load condition experiment of the rolling bearings

利用图6所示峭度作为特征参数序列，进行ARMA模型定阶与参数标定。取前10 s的特征参数序列，基于AIC准则标定阶数p、q。为了保证模型的自回归参数φp与滑动平均参数θq对特征参数x(t-n)的加权影响比较平均，设置约束条件φp≤1及θq≤1；在满足约束条件的结果中，挑选AIC值最小的模型，得到pbest=4，qbest=7，及各阶参数，如表1所示。建立p=4，q=7的ARMA模型，利用compare函数根据对已建立的模型与实测数据进行对比，预测结果如图7所示。

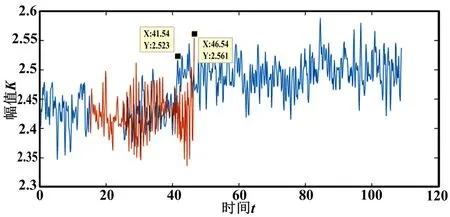
图7 偏载条件下保持架断裂的滚动轴承振动信号AR⁃MA预测结果Fig.7.Prediction results of the vibration signals of cage frac⁃ture under partial load condition experiment of the rolling bearings based on ARMA method

在此试验过程中，发生了滚动轴承保持架断裂的故障。出现故障时测试得到的振动信号有明显的反映，峭度值发生改变。以出现故障时为故障发生起始点，此时距离当前时刻t0的预测时长为T2_pre=21.406 3，对应的总时刻为t2_pre=46.54，实际峭度达2.52，所需的时长为T2_real=16.406 3，对应的总时刻为t2_real=41.54。

4 结论

考虑滚动轴承振动信号的特殊性，采用峭度值的变化表征轴承故障程度的严重性。利用滚动轴承故障程度具有时序性和依赖以前运行状态的特点，构造AR模型参数矩阵，较好地反映出故障程度的变化。峭度-ARMA模型的结合，能较好地提取轴承的故障程度特征，准确地判断故障程度，在滚动轴承的故障诊断中具有较好的实用性。实验结果表明，该方法识别效果比较理想，为滚动轴承故障诊断提供了一种有效的方法。

参考文献：

［1］董玉琼，马波，冯坤.基于振动尖峰能量和频谱分析的滚动轴承劣化程度评估［J］.轴承，2013（3）：45-49.

［2］孟宗，梁智.基于EMMD和BSS的单通道旋转机械故障诊断方法［J］.仪器仪表学报，2013，34（3）：635-642.

［3］康献民，杜春英，康华洲.滚针轴承振动与噪声分析及试验［J］.轴承，2013（8）：38-42.

［4］ Chunchieh Wang， Yuan Kang， Pingchen Shen， et al.Applic-ations of fault diagnosis in rotating machinery by usingtime series analysis with neural network［J］.Expert systems with applications， 2010， 37（2）：1 696-1702.

［5］ Norden E.HUANG，Zheng Shen，Steven R.Long，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc R Soc Lond.A，1998 （454）：903-995.

［6］ Wu Zhaohua， Norden E.HUANG.Ensemble empirical modede-composition a noise-assisted dataanalysis meth⁃od ［R］.Calverton， Center for Ocean-Land-Atmo⁃sphere Studies，2005.

［7］胡爱军，马万里，唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法［J］.中国电机工程学报，2012（11）：106-111.

［8］杨叔子，吴雅，轩建平.时间序列分析的工程应用［M］.武汉：华中科技大学出版社，2007.

［9］赵守国，王素品，邹原.肺音信号非高斯ARMA模型及双谱研究［J］.西安交通大学学报，2001，35（4）：355-359.

［10］孙承杰，刘丰，林磊.基于时间序列聚类和ARMA模型的检索量预测［J］.华南理工大学学报（自然科学版），2011， 39（4）：21-25.