基于CFD技术的风机翼型多目标优化设计*

潘洋洋，林瑞霖，刘伯运

0 引言

轴流风机因其具有高比转速、流量大等特点，被广泛应用到通风、消防排烟等诸多领域。然而当前的轴流风机普遍存在压力低、运行效率差等缺点。因此，有必要对其进行优化改进，以增大压力、提高效率、减少资源浪费[1]。风机翼型的优化设计是改善风机性能的基础，也是风机优化极其重要的组成部分。目前，轴流风机翼型仍大多选用航空翼型，没有形成专属翼型库。在标准翼型的基础上对其几何形状进行优化，从而提高其气动性能，是一种较为便捷且高效的途径。

随着计算机技术及数值计算理论的快速发展，计算流体动力学（Computational Fluid Dynam⁃ics，CFD）得到了广泛的应用。在设计开发过程中采用CFD技术，能够有效降低成本，提高效率[2-4]。

在风机翼型优化设计领域，CFD一般被直接应用到指定翼型的气动性能求解中，而没有系统地在优化设计中得到应用。如何进一步扩宽CFD在风机翼型优化中的应用，使得工程设计工作由依靠经验模式转化为依靠知识化模式，是当下对翼型优化研究的一个重点内容。

在船舶设计行业，近些年兴起了一种基于知识化的设计模式，被称为SBD（Simulation Based Design）技术[5-6]。该技术基于优化设计平台，在设计空间内获取不同的设计参数组合，并由此参数化改变船舶外形，利用CFD对目标函数进行对比评估，以获得最优船舶外形。SBD技术原理如图1所示。

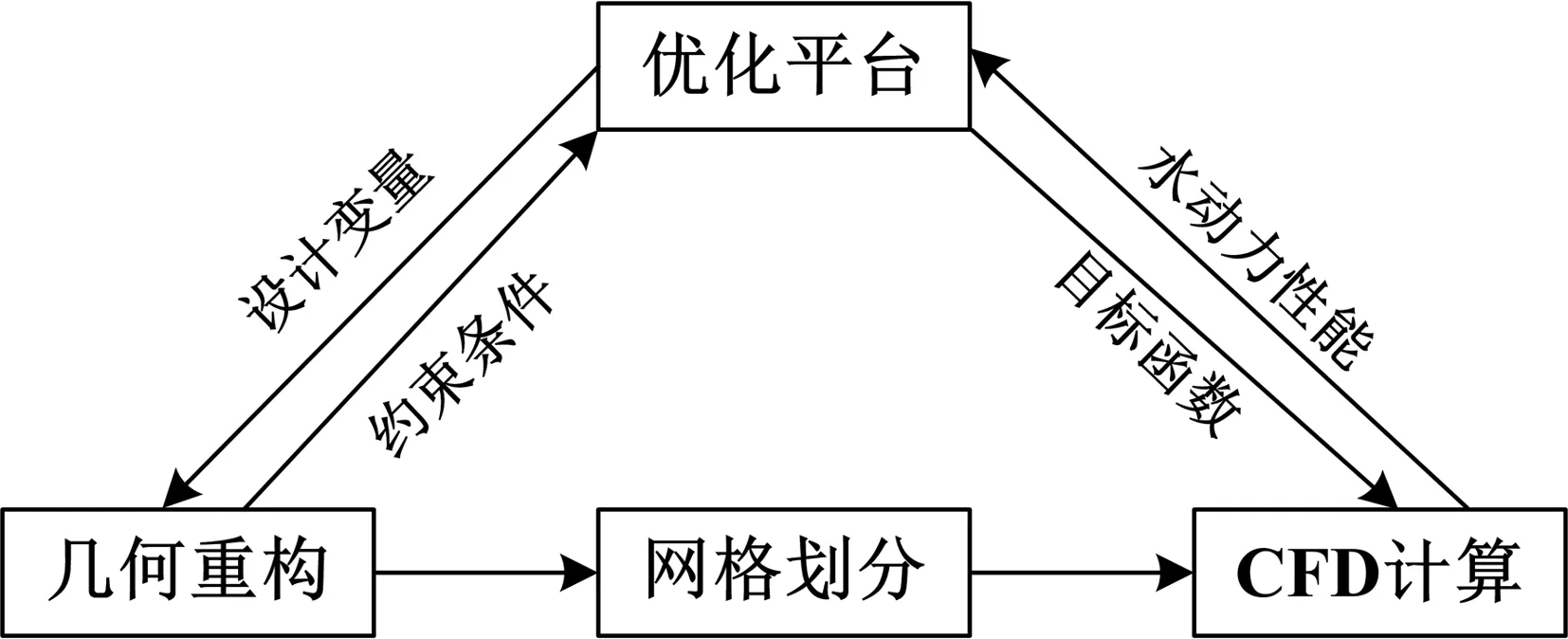
图1 SBD技术原理

风机翼型优化设计过程与船舶的外形设计有着很多相似之处，本文将把SBD技术应用到风机翼型的优化设计之中。基于CFD技术，通过构建优化平台对翼型进行多目标多工况优化，提升翼型的气动性能，为将来对改善风机性能的研究打下基础。

1 多目标优化问题与优化算法选择

多目标优化（Multi-Objectvie Optimization，MOO）是一种通过寻找最优解以同时满足多个优化目标的优化方法[7]。数学定义式如下：

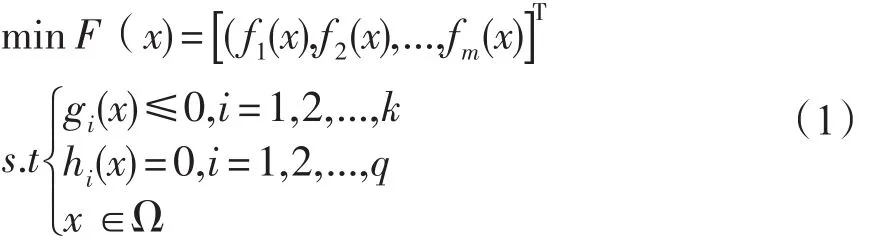
式（1）中：x为优化变量；Ω为优化样本空间；F(x)为优化目标函数； fm(x)为子目标函数；gi(x)和hi(x)为约束条件。多目标优化问题的有效解又被称为Pareto。Pareto解是一种非支配解。求解多目标优化问题就是求优化变量在满足优化约束条件下使目标函数最小值的解，即绝对最优解，但一般情况下，绝对最优解很难获得，而只能求出其Pareto解。

风机翼型的优化是一个多目标问题。在优化过程中涉及到不止一个优化目标函数，比如升力系数、阻力系数、升阻比系数和压力系数等。各目标函数不是孤立存在的，而是经常存在竞争关系，一个目标函数的改善往往会引起其他目标函数的降低。因此，采用什么样的方法对多目标问题进行求解是十分关键的。

当今对多目标问题的求解，多是采用智能算法进行的。其中，多目标遗传算法由于其适用性强、扩展性好而被研究者青睐。与传统的通过对目标函数加权求和，将多目标问题转化为单目标问题进行求解的方法相比，遗传算法可以避免陷入局部寻优，可以很好的在全局寻找最优解，而且具有良好的扩展性，可以方便地与其他软件结合使用。本文采用第二代非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm， NS⁃GA-II）对多目标问题进行求解。这种算法兼具非支配排序和拥挤度两种特点，求解速度快、精度高、鲁棒性能好，能满足翼型优化设计的要求[8]。

2 基于CFD的多目标优化流程与实现

风机的翼型多目标优化过程，即是在约束条件内，利用多目标优化算法，寻找最优的设计参数组合以满足性能参数的目标函数的过程。在优化过程中，样本数据由设计的试验方法生成，再基于代理模型方法建模对性能进行预测。

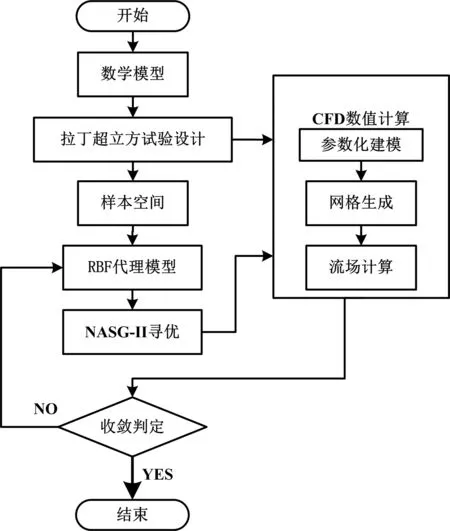
图2 多目标优化流程图

如图2所示，本文设计的多目标优化系统的优化流程主要分为以下几步：

（1）构建优化数学模型，确定优化参数、优化约束和优化目标函数；

（2）选取拉丁超立方设计为试验设计方法，生成试验矩阵，构建样本空间数据库；

（3）由RBF神经网络代理模型获得优化变量与设计参数之间的函数关系；

（4）利用NSGA-II优化算法进行优化计算，得到优化解；

（5）对得到的优化结果进行CFD数值计算，对数值计算结果进行收敛性判断，若符合设计要求，则结束流程，若不符合要求，重复步骤（3），再次计算。

本文中，多目标优化的流程图可由图1表示。

本文在多目标优化的实际求解中，采用Isight软件的软件集成封装功能，实现优化过程。Isight是一套可以将不同类型的软件结合在一起，并能进行多目标优化设计的工具，具有高效、迅速、准确等优点，在工程中经常被使用。

使用Isight软件，将代理模型、试验设计方法、优化算法与CFD等组合起来，自动实现最优方案的求解。利用txt文件描述表征翼型的特征点，作为网格划分软件ICEM的输入，通过录制RPL文件实现几何建模和网格划分的参数化，将得到的网格文件msh作为流场求解软件Fluent的输入，调用修改的TUI文本，参数化进行数值计算，求解翼型的气动性能。基于CFD的气动性能参数化求解流程图可表示为图3。

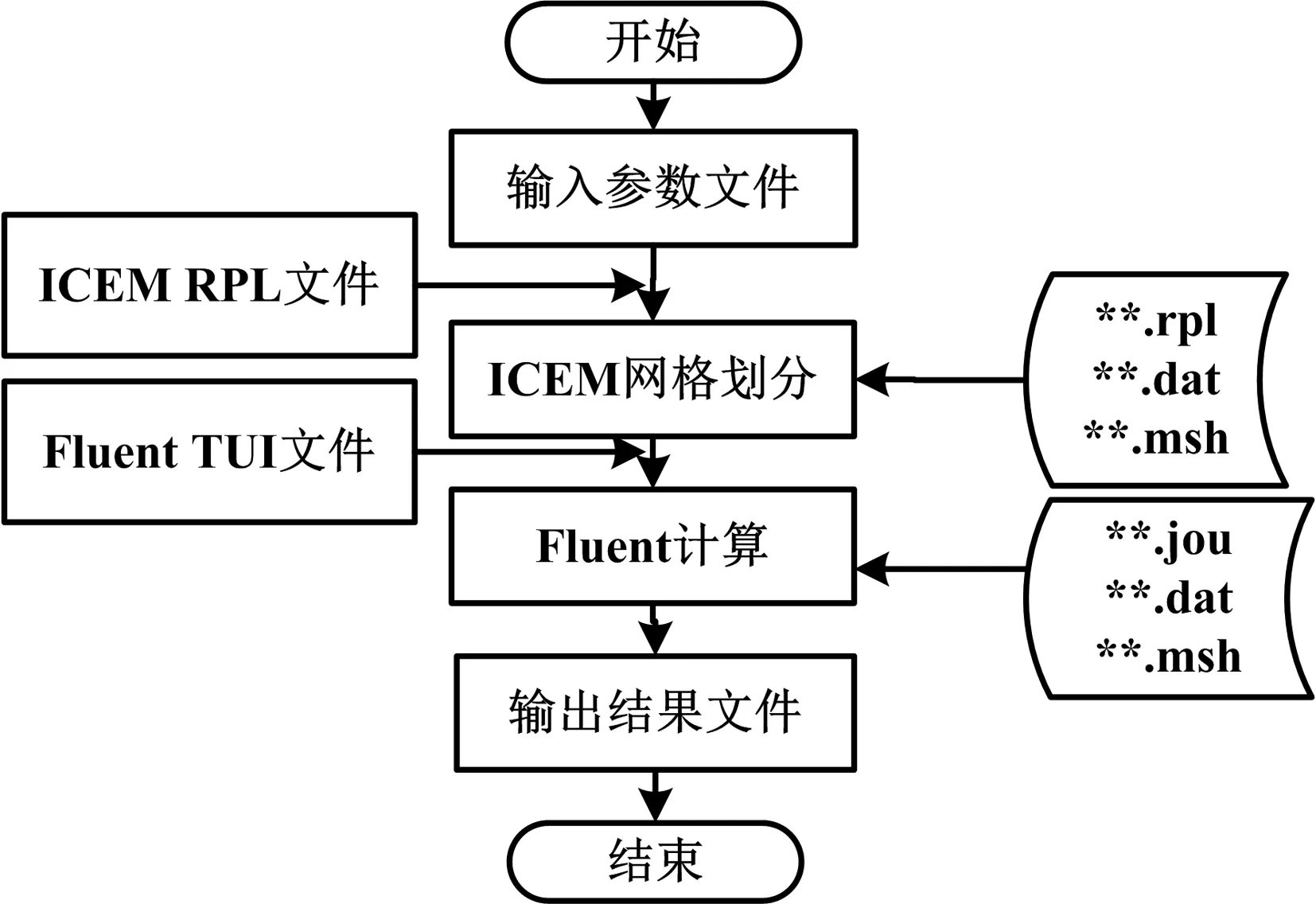
图3 Isight集成CFD软件流程图

3 翼型参数化方法

翼型参数化指的是利用控制参数表征翼型的几何外形，以达到在优化过程中通过改变控制参数就能达到改变翼型几何外形，进而达到改变翼型性能参数的目的。翼型的参数化是翼型优化设计中的极为重要的组成部分，它不仅决定着翼型优化过程中的设计变量的选取，更决定着优化后的翼型各种特征的取值。

Hicks-Henne型函数法是应用最为广泛的一种翼型参数化方法，具有精度高、稳定性强等特点。利用Hicks-Henne型函数法将翼型的上下型线分别进行表示：

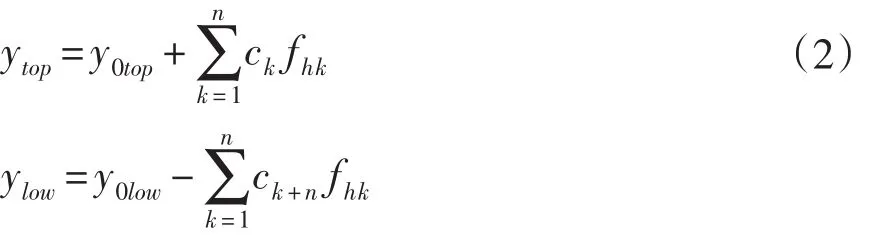
式（2）中，ytop与ylow分别表示翼型函数上下形线，ytop与ylow为对应的基准翼型函数。翼型形线上各点横坐标满足x∈[0,1]。ck为控制参数，是决定翼型厚度和弯度的主要参数，一般取值为[-0.005,0.005][9]。n为控制参数个数，本文中取n=6。 fhk即为Hicks-Henne基函数。由于原Hicks-Henne基函数对翼型后缘的表征效果较差，因此在实际运用中，常采用增加尾缘项k=n的改进表达式如式（2）。

式（2）中，p为控制扰动量大小的参数。参数α主要影响尾缘项型函数的斜率，而参数β则与其衰减速度有关。q为k取值为（1,n）时各型函数波峰点的横坐标，当翼型无量纲即弦长为1时，由n=6可得q的值为{0 .2,0.4,0.6,0.8}，取p=0.3， α=15， β=15作出对应的Hicks-Henne基函数图像如图4。

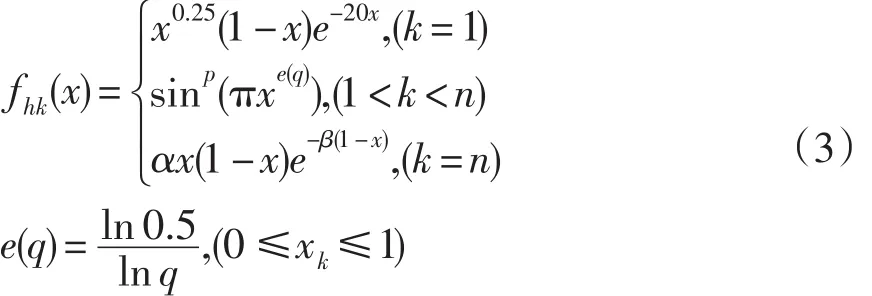
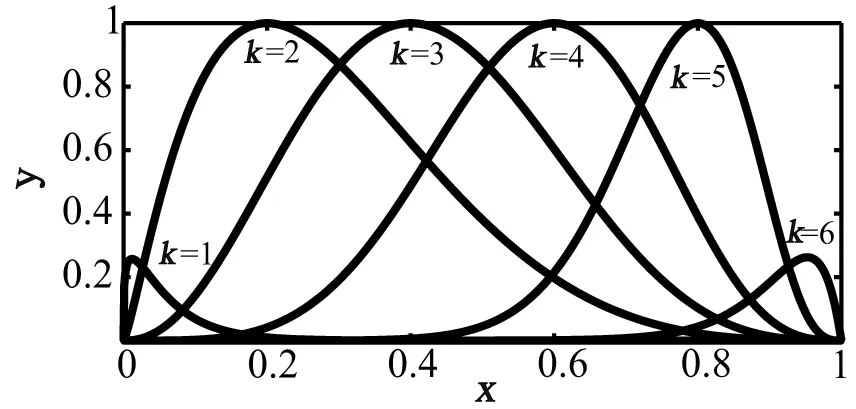
图4 改进后的Hicks-Henne型函数图像

4 优化算例与结果分析

初始翼型：NACA0018标准翼型。

工况条件：三个工况点，翼型冲角分别为2°，4°和6°，在此三个工况点下对翼型进行多目标气动性能的优化，翼型特征长度为0.1 m。

参数化方法：利用改进后的Hicks-Henne对翼型压力面和吸力面分别参数化表示，选取n=6。

优化设计变量：采用Hicks-Hence扰动法控制变量，设计变量共12个，分别记为cki(i=1,2,...,12)。

优化约束：每一个控制参数cki范围均为[-0.005，0.005]。

优化目标：本例中，优化目标设置为两个：一个是三冲角工况状态下的加权升力系数CL最大，另一个为一个是三冲角工况状态下的加权升阻比系数μx最大。结合实际工作要求，轴流风机翼型冲角一般设计为4°左右[10]。本文选取的三个工况冲角值分别为2°，4°与6°。各工况点权重可由权的最小平方法（Weighted Least-square Meth⁃od，WLSM）结合最小二乘法计算确定[11]。本文分配结果可表示如下式：

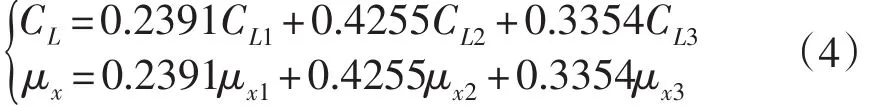
NSGA-II设置种群数量为20，最大繁殖代数为40，交叉率0.9，变异率0.7。在前文中已经进行了介绍，多目标问题很难求得最优解，一般只能获得其Pareto解。对于每一个翼型优化算例，能求算出多少个符合最优适应度的结果是不可预估的。只要迭代次数够多，迭代次数够长，即可以获得较多符合条件的优化结果。对本文而言，研究的目的是探索翼型优化的方法而不是对具体某一翼型进行最优设计。因此，本文只对一种优化结果进行分析。优化结果如图5和表1所示，对应的设计变量取值为：ck1=-0.000 15，ck2=-0.002 17， ck3=0.004 19， ck4=0.003 58， ck5=0.002 13，ck6=0.000 54，ck7=0.000 27，ck8=-0.001 33， ck9=-0.000 34， ck10=0.002 91，ck11=-0.000 78，ck12=0.001 76。

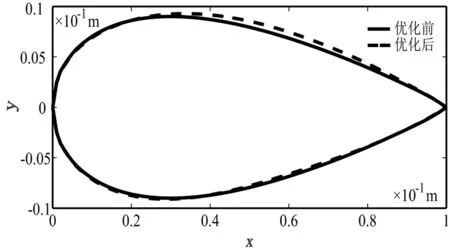
图5 优化前后翼型外形对比

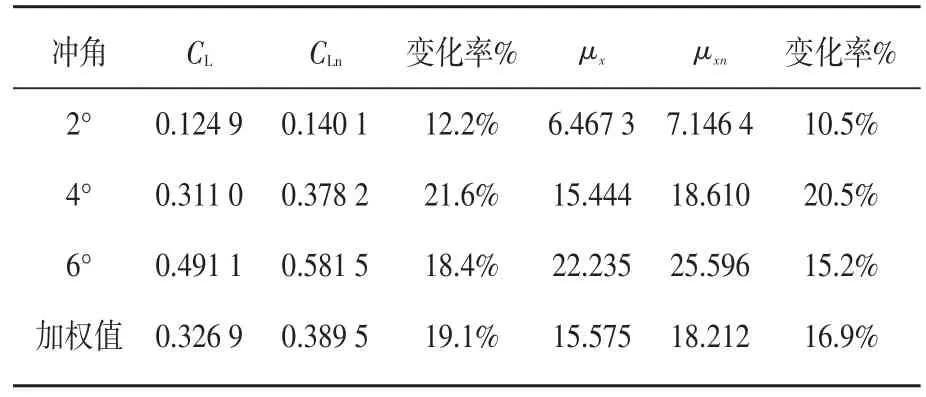
表1 优化前后目标函数值对比

对比NACA63-25翼型单目标优化前后外形，可以发现翼型的前缘点附近变化较少，而中后部变化较大，厚度有了一定程度的提升。较原翼型相比，弯度有所增加。

由表1，对于优化的三冲角工况状态下的加权升力系数与加权升阻比系数。三个工况点下的升力系数与升阻比系数均得到了提升，而且提升幅度排序和对应加权升力系数表达式与加权升阻比系数表达式中各工况点权重因子大小排序相同，升幅大小依次是4°冲角工况点，6°冲角工况点与2°冲角工况点。最终，加权升力系数提升了19.1%，加权升阻比系数也提升了16.9%，优化效果较为显著。

5 结语

针对轴流风机翼型的优化问题，本文构建一套了基于CFD的翼型多目标优化设计系统。将船舶设计行业的SBD技术引入到翼型优化中来，采用优化后的Hicks-Henne型函数化对翼型进行了参数化表示。利用Isight软件对ICEM和Fluent等软件进行了集成，实现了翼型气动性能的参数化求解，在此基础上使用NSGA-II算法进行寻优。为验证系统性能，采用标准翼型NACA0018，以三种冲角工况的加权升力系数和加权升阻比系数为目标进行了多目标优化设计，结果表明二者分别提升了19.1%与16.9%，优化效果良好，证实了多目标优化方法的有效性，为后续对轴流风机的性能改善打下了基础。

本文设计的多目标优化系统具有一定的扩展性，也可以应用到其他翼型或者流体机械的优化设计中。

参考文献：

［1］黄友根.低压轴流风机多目标多工况优化设计研究［D］.武汉：华中科技大学，2015.

［2］夏陈超.基于CFD的飞行器高保真度气动外形优化设计方法［D］.杭州：浙江大学，2016.

［3］林伟涛，黄坚，刘桂雄.汽车散热器流场特性CFD数值模拟与分析［J］.机电工程技术，2016，45（09）：96-99.

［4］兰林强，罗伟林.基于参数化建模和CFD数值模拟的船舶球鼻艏优化设计［J］.机电工程，2016（11）：1329-1333.

［5］Campana EF，Peri D，Tahara Y，et al.Numerical opti⁃mization methods for ship hydrodynamic design ［J］.Transactions-Society of Naval Architects and Marine En⁃gineers，2009，117：30-77.

［6］李胜忠.基于SBD技术的船舶水动力构型优化设计研究［D］.武汉：中国舰船研究院，2012.

［7］ Trivedi A，Srinivasan D，Sanyal K，et al.A Survey of Multiobjective Evolutionary Algorithms Based on Decom⁃position［J］.IEEE Transactions on Evolutionary Com⁃putation，2017，21（3）：440-462.

［8］李海燕，井元伟.基于NSGA-II的具有多目标子学科的协同优化方法［J］.控制与决策，2015，30（8）：1497-1503.

［9］王建军，高正红.HicksHenne翼型参数化方法分析及改进［J］.航空计算技术，2010，40（4）：46-49.

［10］ JB/T 10281-2014.消防排烟通风机［S］.

［11］王欣星，张安明.权的最小平方法在土地利用现状评价中的应用——以重庆市黔江区为例［J］.中国农学通报，2012，28（02）：234-239.