飞机EMA行星轮减速器多学科协同优化设计*

夏泽斌，段富海,※，金 霞，安 玮

行星轮减速器因其体积小，传动比大，承载能力强和传动效率高等特点，越来越广泛应用在航空航天、工程机械、矿山机械、数控设备等各种机械传动系统中。飞机功率电传用机电作动器（Electro-Mechanical Actuator，EMA）要求功率重量比大、运行可靠稳定且使用寿命长[1-2]，这对其行星轮减速器的设计提出了很高要求。行星轮减速器的性能是EMA高质量完成工作的关键，而体积、强度及刚度等都是衡量行星轮减速器性能优劣的重要指标，这些指标往往是相互冲突的，所需的约束条件又耦合在一起，使得行星轮减速器的设计变得复杂。如何兼顾上述性能目标和质量目标，并求得总体设计的最优解是工程设计人员不断研究与探讨的问题。

一直以来，设计人员常用遗传算法、罚函数法等对减速器的各参数进行优化。杨奇[3]等人基于遗传算法对行星轮减速器进行了优化设计，提出了以单参数最大效能体积比来确定最佳短幅系数的方法，并得到了设计结果。西庆坤[4]等人利用MATLAB遗传工具箱解决了摆线针轮行星减速器传动效率低，结构不紧凑的问题。于明[5]等人以体积最小为优化目标，对减速器进行了优化设计，但只考虑减速器的外部尺寸，没有考虑内部结构对减速器的影响。随着学者们对优化算法的深入研究，人们发现遗传算法存在对新空间的探索能力有限、计算复杂、难以处理非线性约束、稳定性差等缺点；罚函数法存在起始点难以选择、罚因子难以确定等缺点。另外对EMA的研究多集中在电机与控制学科，对机械学科的文献相对较少。为进一步提高行星轮减速器的性能，本文探索利用多学科协同优化设计（Collaborative Optimization，CO）方法来完成行星轮减速器的优化设计。

CO方法充分利用不同学科之间的相互作用以及协同机制，将单个学科的分析与优化同整个系统中互为耦合的其他学科的分析与优化结合起来，能够将涉及的几个学科之间的耦合关系分析清楚，可很好地解决不同学科之间的冲突性以及约束的复杂性，从而得到适合条件的全局最优解[6]。利用多学科CO设计方法来完成行星轮减速器优化，可以将复杂的行星轮减速器设计分解为若干简单子任务，来完成原有的设计任务，这样可减少原有设计复杂度，更易得到全局优化解。设计空间缩减协同优化算法（Design Space Decrease Collaborative Optimization，DSDCO）是一种改进的协同优化方法[7]，它根据子空间优化结果，删除不可行求解空间，选取系统级优化解，通过子空间循环迭代优化计算，直至系统级优化解符合收敛条件。

本文以EMA摆线针轮行星轮减速器为研究对象，以符合设计要求的结构尺寸和应力约束条件为基础，以行星轮减速器体积最小为目标，建立数学模型，使用DSDCO算法对EMA进行多学科协同优化，并对优化结果进行分析。

1 行星轮减速器的数学模型

1.1 确定设计变量

某型飞机EMA所用减速器为摆线针轮行星减速器，其结构如图1所示。通过分析影响摆线针轮行星减速器的主要参数，同时考虑优化设计的建模，选择针轮分布圆直径DZ、针齿套外径dZ、摆线轮宽度B、转臂轴承外径D1和柱销直径dp作为设计变量，其他参数均为设计常量，这5个设计变量分别独立，决定了摆线针轮行星减速器的体积，即摆线针轮行星减速器优化设计的设计变量：

X=[X1X2X3X4X5]T=[DZdZB D1dp]T

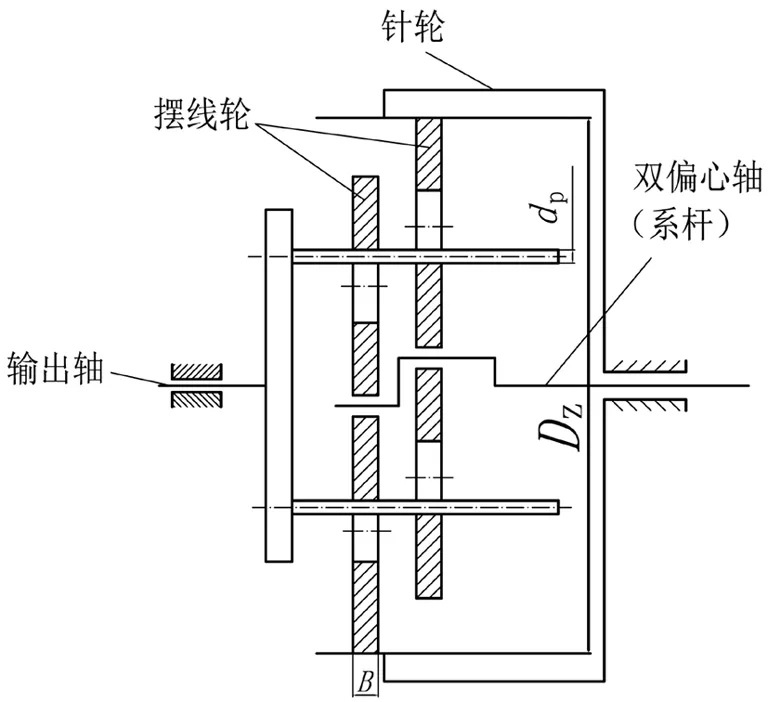
图1 摆线针轮行星减速器结构示意图Fig.1 Cycloid reducer structure diagram

1.2 建立目标函数

摆线针轮行星减速器优化设计的目标既可以是性能指标，也可以是总体的结构尺寸。本文采用在给定传动功率和传动比时，满足强度及其他几何尺寸要求条件下摆线轮的体积最小，作为摆线针轮行星减速器设计的目标函数[8-10]，以便使减速器结构紧凑，功重比大。摆线轮的尺寸决定了摆线针轮行星减速器的结构大小。

摆线轮的体积可认为是齿根圆内的圆盘体积加上摆线齿部分的体积，减去转臂轴承占据的体积和柱销孔的尺寸，可推得摆线轮体积为：

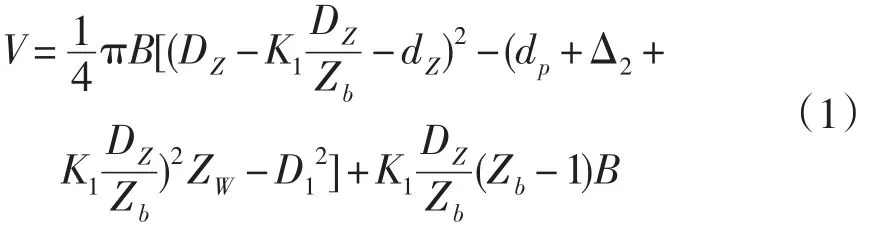
于是得到摆线针轮行星减速器优化设计的目标函数:

式（2）中：Zb为针轮齿数，其数值为传动比加1；ZW为柱销数目；Δ2为柱销套壁厚；K1为短幅系数。

1.3 建立约束条件方程

1.3.1 摆线轮齿廓不根切条件

为避免齿廓发生根切，针齿套外径dZ与针轮分布圆直径DZ的比值应当小于理论齿廓最小曲率

半径系数amin，即

得约束条件为：

式（3）中：Zg为摆线轮齿数；K1为短幅系数，是摆线针轮行星传动的重要系数。1.3.2摆线轮厚度的限制条件

摆线轮厚度一般为：

得约束条件为：

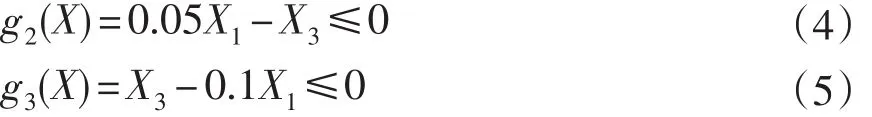
1.3.3 摆线轮与针齿的接触强度条件

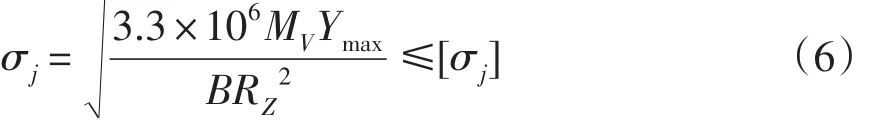
1.3.4 针齿销的弯曲强度条件

对于双支点针齿销的弯曲应力为：

式（6）中： MV为输出轴的阻力矩，

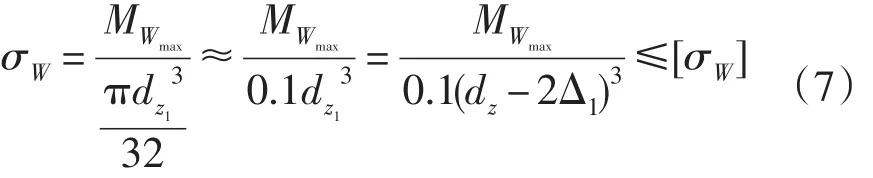
式 （7） 中 ： dz1

针齿销上最大的弯矩数值为：

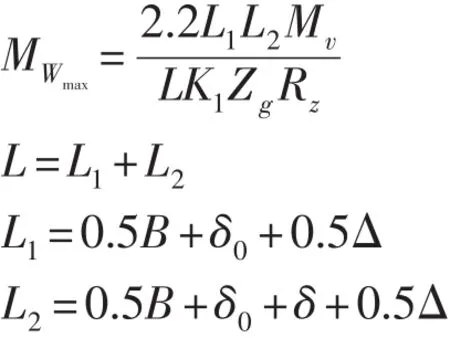
式中：δ0为摆线轮与针齿壳侧面间的间隙，一般取δ0=4 mm；δ为两摆线轮间隔环的厚度，δ=B-b，b为轴承的宽度；Δ为针齿壳侧面的壁厚，一般为dZ＜Δ＜B。

约束条件为：

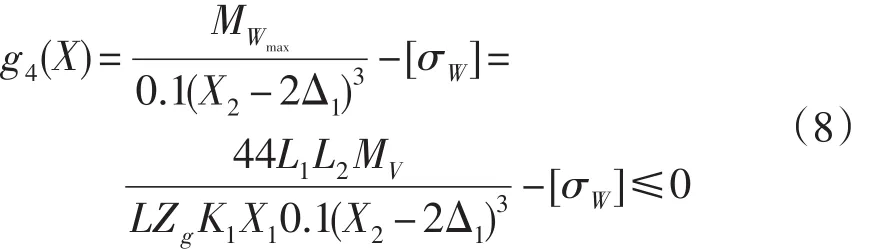
1.3.5 针轮分布圆直径的限制条件

针轮分布圆直径的设计对减速器结构尺寸和承载能力有很大的影响，一般是根据输出轴的阻力矩，由经验来确定和选择的。其经验公式为:

1.3.6 柱销的弯曲强度

卧式结构的柱销常规设计是悬臂安装的[11]，其柱销所受的最大弯曲应力需满足:

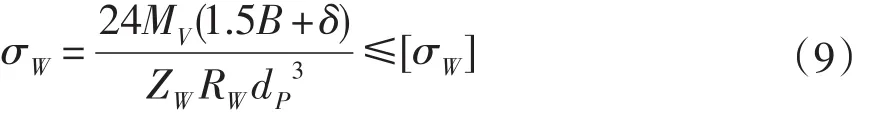
式（9）中：柱销分布圆半径RW：

约束条件为：

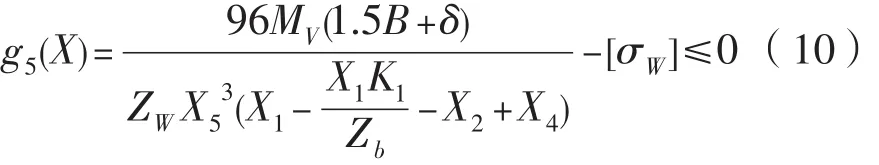
1.3.7 柱销套与柱销孔的接触强度条件

柱销套与柱销孔的接触应力由赫兹公式，经整理得到，接触强度条件为:

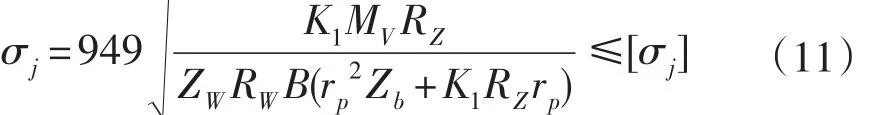
式（11）中：柱销套半径rp=0.5dp+Δ2。

约束条件为：

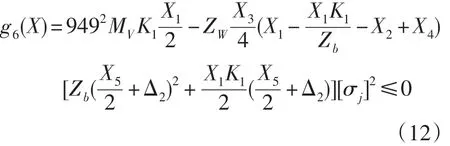
1.3.8 柱销孔最大直径的限制条件

为保证摆线轮有足够的强度，在两个柱销孔之间，柱销孔与转臂轴承外径孔之间，又有一定的厚度Δ0，工程中一般取Δ0=0.03DZ，其限制条件为：

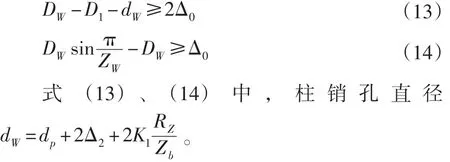
约束条件为：

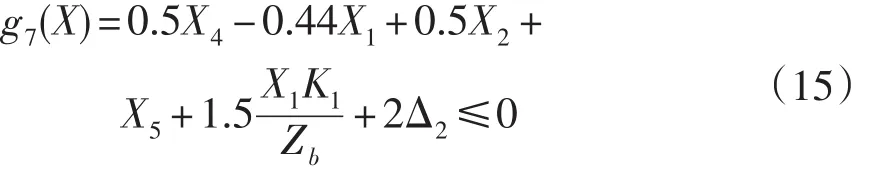
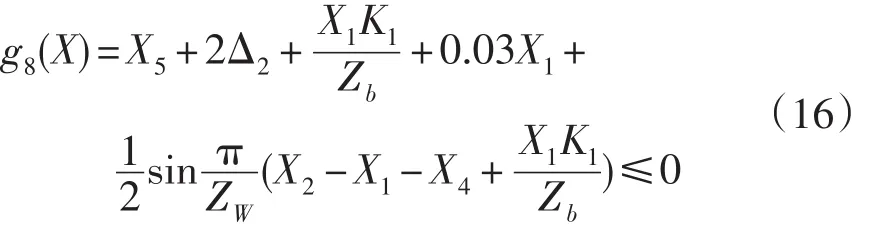
2 多学科协同设计优化及其算法

2.1 多学科协同设计优化

多学科协同优化（CO）是一种针对复杂系统设计问题的多级式优化方法，它将复杂的系统设计问题分解为一个系统级和并行的几个子系统级问题，并通过系统级约束条件来协调各子系统之间的共享设计变量和耦合状态变量[12-13]。CO主要思想是：在子系统优化时可以暂时不考虑其它学科的影响，只需要满足该子系统级约束，子系统级优化目标是使该子系统优化结果与系统级优化提供的目标差异值达到最小；而各个子系统级优化结果的不一致性由系统级优化来协调，通过系统级优化和子系统级优化之间多次迭代，最终得到一个符合学科间一致性要求的系统最优化设计方案。根据CO思想，减速器的子系统划分可以按照约束条件所属学科进行，由减速器优化模型可知，约束条件包含了机械结构以及力学两个不同的学科。可将减速器优化问题划分为两个子系统：机械结构学科和力学学科。在两个子系统内分别进行优化设计，并把子系统优化结果传递到减速器系统级优化。相比于其他优化过程，CO可解决复杂耦合问题并简化复杂计算过程。

将多学科协同优化应用于减速器，其本身就是考虑满足不同学科下的约束条件所需目标的最优解，减速器设计也由直觉、经验设计变为更有效率、更符合使用要求的理性设计。

2.2 DSDCO算法求解思路及其特点

多学科协同优化有多种算法，如ECO、CLA-CO、DSDCO等。金霞[7]等提出的设计空间缩减协同优化算法（DSDCO）适用变量有界的多学科优化问题，具有对起始点无要求、计算时间快、对约束条件凸凹性没有要求等特点。DSDCO根据子系统优化结果，在原问题的求解空间中去除子系统计算所得的不可行域，将剩余的求解空间作为系统级优化的求解空间进行系统级优化计算。随着迭代的继续，求解空间不断更新系统级变量边界，在原求解空间中不断去除不可行域，但始终包含完整的原问题可行域。当系统级优化解满足收敛条件时，得到原问题的全局最优解。该方法对于原问题约束函数的凸性没有限制，在系统级优化公式中，用变量边界代替了传统协同优化中的一致性等式约束，使系统级优化得到有效的简化，很好地解决了传统协同优化设计系统级优化求解困难的问题。但该算法需要在原问题的设计空间内不断更新优化设计空间，故仅适用于变量有界的多学科设计优化问题[7,14-15]。

某多学科优化问题含有n个系统级设计变量，z个子系统。在k-1次迭代优化时，系统级优化点为，对应的子系统优化空间为OBJ*(k-1)，系统级求解得到的子空间集为L*(k-1)。因子系统个数为z，子系统级优化可得到z个子系 统 优 化 解（i=1,2,…,n）。 定 义为

为去除当前求解子空间L*(k-1)中不可行域，需要沿着各个坐标轴去除不可行域。为最大限度的去除不可行域，每个坐标方向上的上下界限分别为：

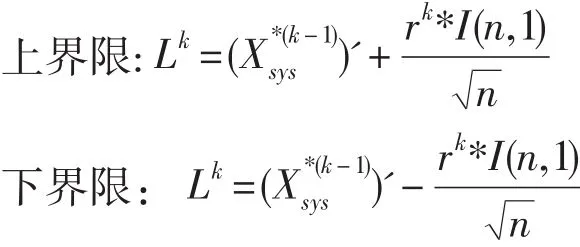
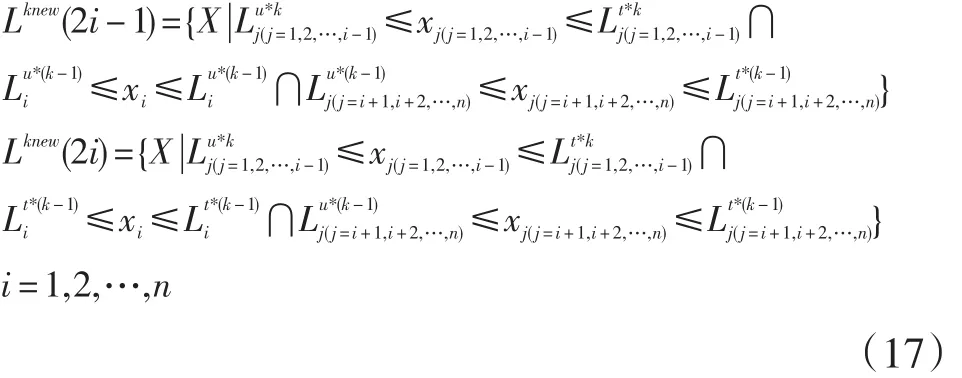
将Lknew传递到系统级求解子空间并更新系统级求解子空间集Lk。由以上操作得到新的求解空间，进行优化求解过程，循环迭代此过程，直至得到的系统级优化结果满足收敛条件。但是需要注意的是，Lnew中若出现不符合逻辑的空间，需删除不符合逻辑的求解空间。比如，在更新得到的求解空间中，如果某变量上界或下界超出L*(k-1)中该变量的上下界，则用L*(k-1)中相应界限值将其代替。

综合DSDCO特点以及其求解思路，该方法适用于优化摆线针轮行星减速器的结构设计变量，可以综合考虑不同学科的影响，满足特殊设计要求以及约束条件，获得最优设计，有效提高设计质量，降低研制费用，缩短设计周期。

3 结果及分析

3.1 减速器优化过程及结果

摆线针轮行星减速器输入功率NH=4 kW，许用弯曲应力[σN]=15 000 N/cm2，许用接触应力为[σj]=85 000 N/cm2[16]，主动轴转速 nH=1 440 r/min，传动比为i=29，针齿壳侧面的壁厚Δ=14 mm，针齿套壁厚Δ1=2.5 mm，柱销套壁厚Δ2=5 mm，短幅系数K1=0.69，轴承的宽度b=20 mm。

该设计优化问题可表示为：

DSDCO算法将原问题分解为一个系统级优化问题和两个子系统级优化问题。子系统1的约束为g1、g2、g3、g7、g8，设计变量为X1、X2、 X3、 X4、 X5；子系统2的约束为 g4、g5、 g6，设计变量为 X1、 X2、 X3、 X4、 X5；系统级设计变量为X1、X2、X3、X4、X5。将减速器体积最小作为目标函数，编写DSDCO优化程序，运行程序，循环过程中得到部分数据如表1。

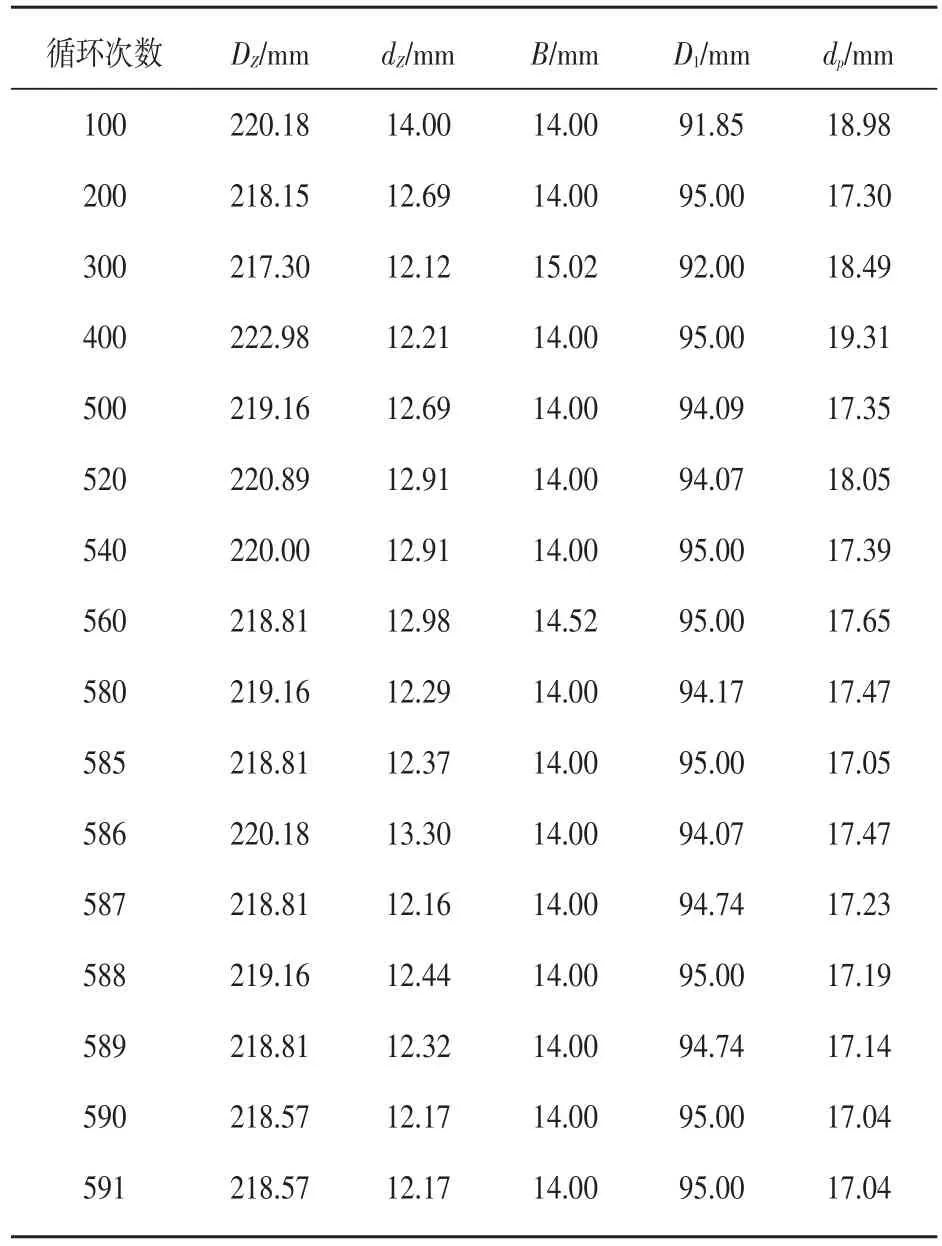
表1 循环过程中部分数据Table1 Somedatain thecyclic process

最后得到最优解如表2所示。

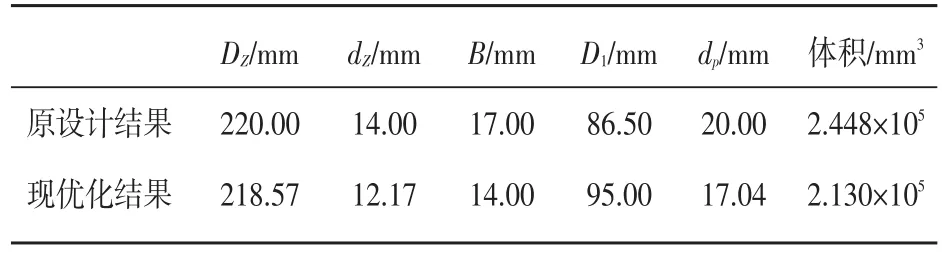
表2 摆线针轮行星减速器优化结果Table2 Cycloid reducer optimization results

3.2 优化结果分析

与原设计结果比较可得，由DSDCO计算得到的体积相对减少量为（2.448-2.130）/2.448×100%=12.99%。此优化结果说明采用DSDCO对摆线针轮行星减速器进行优化，能够在保证减速器接触强度以及弯曲强度的前提下，使的减速器结构变得更为紧凑。使用该目标函数、约束条件以及DSDCO算法进行的优化设计有效，DSDCO可为减速器优化或其他类似结构的多学科优化提供参考。

4 结论

（1）以摆线针齿行星轮减速器为研究对象，以减速器体积最小为优化目标，以减速器内部机构尺寸关系和各个部位的应力要求为约束条件，建立的减速器优化设计模型，能够很好地体现减速器内部结构和应力要求，能够真实地反映减速器的设计情况，切合实际。

（2）采用DSDCO优化设计后减速器的体积明显减小，得到的设计参数更为科学合理，弥补了当前减速器设计中设计变量主要依据传统经验设计方法的不足。因此达到了优化飞机EMA摆线针齿行星轮减速器的目的。

（3）运用DSDCO算法对减速器模型进行优化，很好地解决了包含两个学科的耦合问题，求解简单方便，减少设计复杂度，更易得到全局优化解。

（4）本文研究对EMA行星轮减速器的设计具有一定的理论指导和实际应用价值，所用DSDCO算法为解决含有多个学科的耦合优化问题提供了一种新方法，具有一定理论价值。

参考文献：

［1］LIQ，FENGL M，TANGL，et al.Structural Resonance Analysis of MEA Servo System with Low Frequency Mod⁃al Load ［C］.//2016 IEEE/CSAA International Confer⁃ence on Aircraft Utility System （AUS）， October 10-12，2016，Beijing，China.

［2］ ZHOU Y，WANG M L，ZHANG C Q.The Design of BLDCM Controller for EMA based on Fuzzy PID Control［C］.//28th China Conference On Decision and Control（2016CCDC），May 27-31，2016，Yinchuan，China.

［3］杨奇，王福伟，何蕾，等.摆线针轮行星减速器最佳短幅系数的确定及优化［J］.应用科技，2010，37（05）：1-4.

［4］西庆坤，卢万强，曹素兵.基于遗传算法的摆线针轮行星减速器优化设计［J］.机械传动，2014，38（09）：87-90.

［5］于明，徐承妍.基于MATLAB的摆线针轮传动的优化设计［J］.现代制造工程，2010（08）：141-143.

［6］李响.多学科设计优化方法及其在飞行器设计中的应用［D］.西安：西北工业大学，2004.

［7］金霞，段富海，辛大志，等.基于设计空间缩减的多学科协同优化新方法［J］.机械工程学报，2015，51（11）：133-141.

［8］祁燔，刘雪东，杜明星，等.NGW行星齿轮减速器动力学仿真与行星架减量化设计［J］.制造业自动化，2015，37（12）：99-101，105.

［9］焦陈磊，马世泰，杨鑫德，等.基于Ansys和Matlab的NGW51行星齿轮组的分析与优化［J］.起重运输机械，2017（03）：20-23.

［10］朱增宝，季军，李灿，等.基于高传动效率的行星齿轮传动系统优化设计［J］.煤矿机械，2013，34（01）：32-33.

［11］梁凯翔，王忠素，田士涛，等.摆线针轮行星减速器优化设计和仿真分析［J］.机械传动，2017，41（03）：155-165.

［12］ Park H，Chung J，Behdinan K，et al.Reliability and possibility based multidisciplinary design optimization for aircraft conceptual design［C］.//11th AIAA Avia⁃tion Technology， Integration， and Operations（ATIO） Conference， Virginia Beach， VA.AIAA 2011-6960.

［13］ Lee CH，Mavris ND.Bayesian collaborative sampling for aero propulsion design of an engine and nacelle［C］.//48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit， Atlanta， Georgia.AIAA-2012-3997.

［14］金霞，段富海，江秀红.一种求解变量有界非线性规划的全局最优解新方法［J］.上海交通大学学报，2016，50（6）：861-867.

［15］ JIN X，DUAN F H，CHEN P，et al.A robust global optimization approach to solving COproblems-enhanced design space decrease collaborative optimization［J］.Structural and Multidisciplinary Optimization， 2017，55（6）：2305-2322.

［16］杨可桢，程光蕴，李仲生，等.机械设计基础（第5版）［M］.北京：高等教育出版社，2006.