新旧刚架拱桥横向连接前后力学性能分析
2018-04-25于龙
于 龙
(广西壮族自治区林业勘测设计院,广西 南宁 530011)
刚架拱桥是在1976年由交通部公路科学研究院研究出的一种新桥型[1],这种桥型节省钢材,可以充分发挥混凝土的抗压能力,结构质量轻,便于水上施工,在20世纪80年代得到了广泛应用,但是,随着中国经济的发展,交通运输行业日益发达,公路桥梁上的超载现象十分严重,而刚架拱桥横向联系不强,超载潜力小,故现在大部分20世纪修建的刚架拱桥出现了不同程度的损害[2],主要的病害包括拱肋、拱脚、横向连接构件出现裂缝、桥面铺装严重破损等[3],故研究刚架拱桥加固及其力学性能分析,有助于结构安全。
某座刚架拱桥,因道路扩宽,其旁修建了相同尺寸的另外一座刚架拱桥,施工中并没有将两座刚架拱桥横向连接,考虑到可靠的横向连接可能有助于使结构受力分配更加合理,因此,采用数值模拟软件ANSYS,建立两座刚架拱桥相连接前后的模型,分析其静力特性及动力参数,研究将新旧刚架拱桥连接是否合理。
1 刚架拱桥建模
该旧刚架拱桥2#桥与新刚架拱桥1#桥的结构、尺寸、材料一致,L/2上部构造设计图如图1所示,跨中横向示意图如图2所示,拱腿、主拱厚度均为30 cm,横向共有五片主梁,相邻主梁间有11片15 cm×50 cm×150 cm横梁及2片15 cm×150 cm×150 cm横梁进行连接,相邻拱腿间有2片15 cm×50 cm×150 cm横梁进行连,设计荷载为公路-I级。现状两座桥未设置横向连接,拟采用湿浇钢筋混凝土对1#桥、2#桥进行连接,连接构件长度为3.5 m。
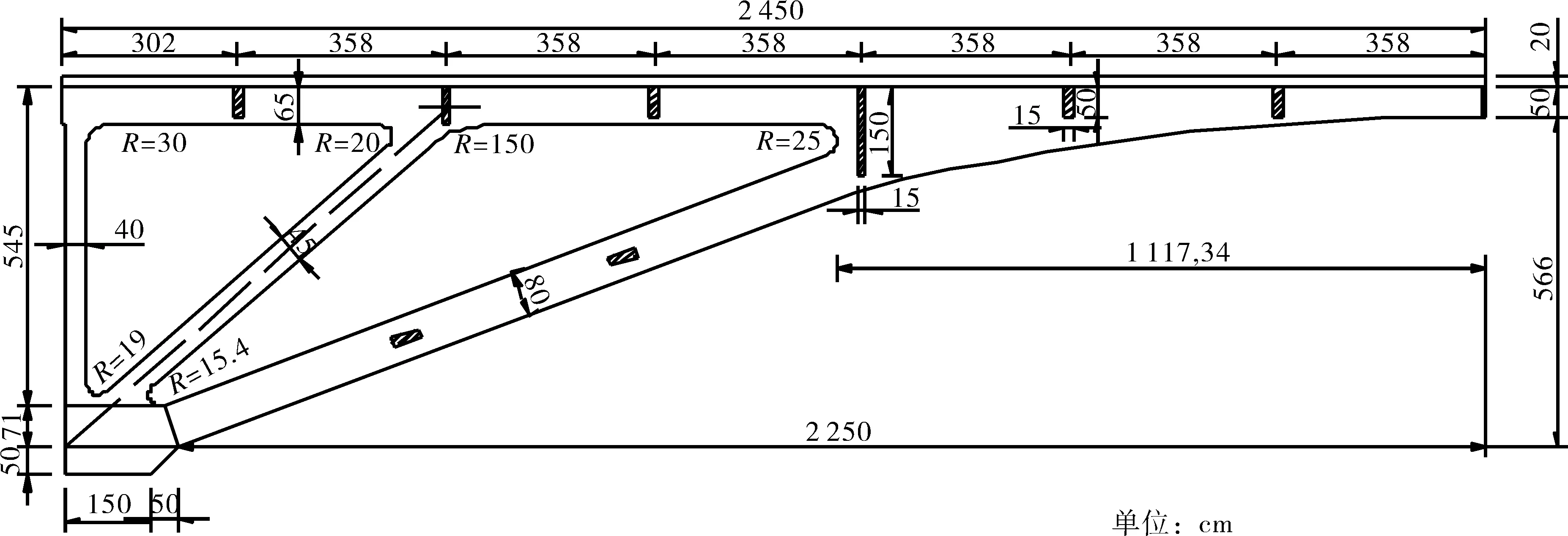
图1 某刚架拱桥L/2上部构造设计图

图2 刚架拱桥跨中横向示意图
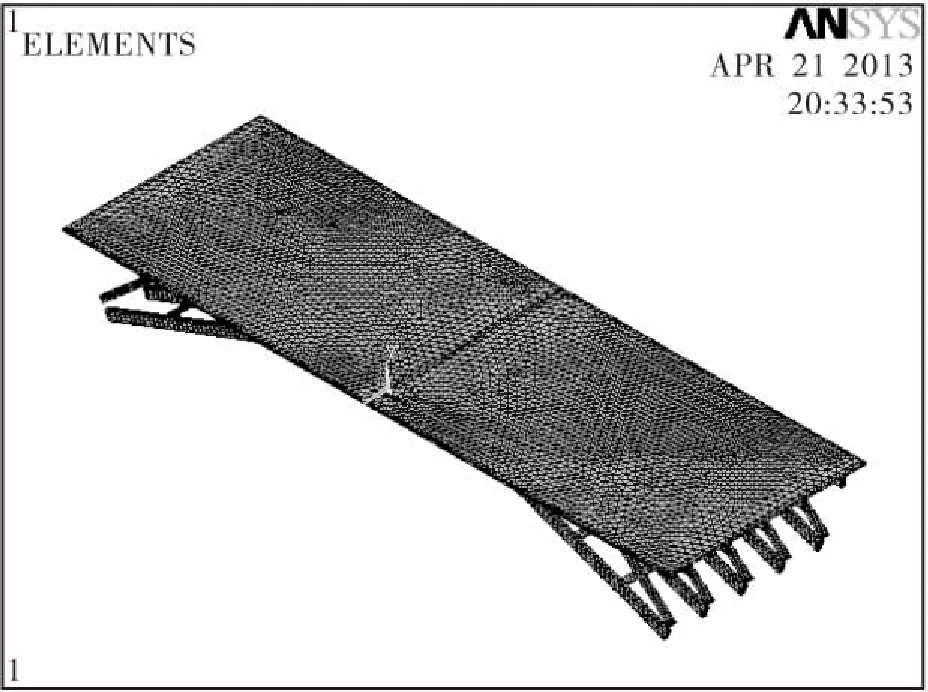
图3 连接前单座刚架拱桥模型图
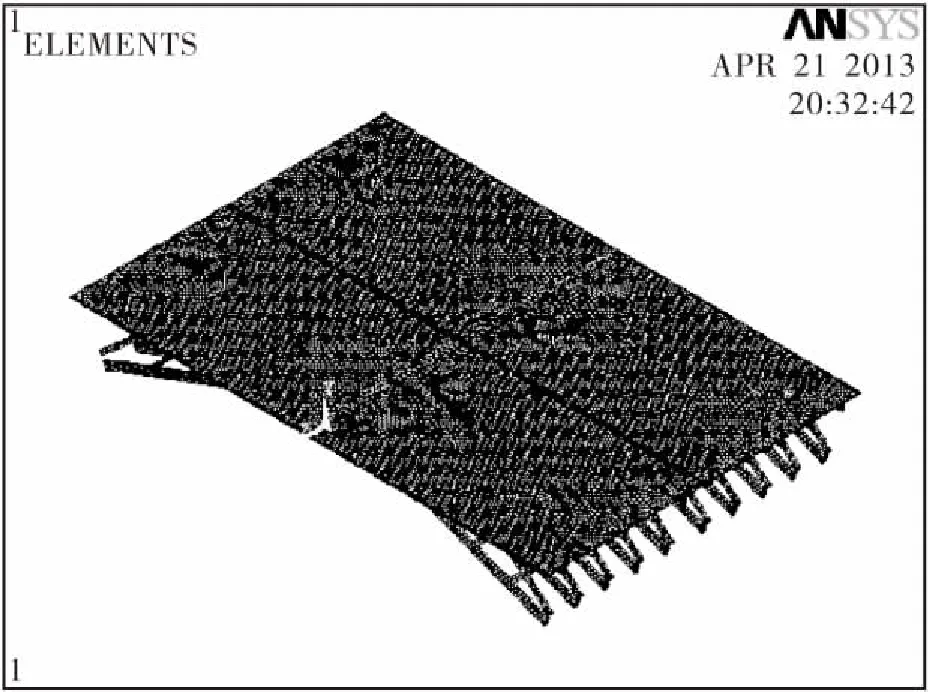
图4 连接后双座刚架拱桥模型图
采用ANSYS建模,连接前的1#、2#桥完全对称,故简化为单座刚架拱桥模型(如图3所示),连接后双座刚架拱桥模型如图4所示。对应构件的弹性模量模型取值相同,采用SOLID45单元,拱肋、斜撑、拱腿、弦杆有C40混凝土和钢筋组成,配筋率为6.14%,按公式(1)进行整体弹性模量的计算[4],得出弹性模量为4.28×1 010 Pa,密度为2.83 kg/m3,泊松比为0.3。
ECS=(1-η)EC+ηES
(1)
式中,ECS——构件换算弹性模量;
EC——混凝土弹性模量;
ES——钢筋弹性模量;
η——构件的配筋率,η<2%时不考虑钢筋对混凝土弹模的影响[5]。
由于桥面铺装、横隔梁、连接构件的配筋率较低,因此其弹性模量取为C30混凝土弹性模量,即为3×104MPa,密度取为2.50×103kg/m3,泊松比为0.3。
固结模型拱脚端部,铰接斜撑端部,弦杆端部仅加竖向约束,采用自由网格划分,单座刚架拱桥模型共划分出25 994个单元,连接的双座刚架拱桥模型共划分出49 073个单元。
2 两桥连接前后横向连接强度分析
2.1 有限元模拟原理
在构件的弹性工作阶段,构件所受荷载与变形成正比[6],故通过公式(2)计算桥梁的荷载横向分配系数。
(2)
式中,ηj,i——单位荷载作用在j#梁时,i#梁的荷载横向影响坐标;
ui,j——此时i#梁的位移。
2.2 结果分析
通过计算得到各梁的荷载横向分布影响竖向坐标如表1所示,从表1得到1#~3#梁连接前后的荷载横向分布影响图如图5所示,4#~5#梁连接前后的荷载横向分布影响图如图6所示。从图中可以看出,两桥连接前后,1号桥1#~3#梁的荷载横向分布并没有明显变化,这是由于1号桥1#~3#梁离连接构件的距离较远,而刚架拱桥的横向连接偏弱,故1#~3#梁上的荷载对2#桥的影响较少,而4#~5#梁的荷载横向分布在连接后变化很大,由于连接构件4#~5#梁的部分荷载传到2#桥,故4#~5#梁的荷载横向分布趋于均匀,减小了边梁的受力,对构件有利。

表1 各梁的荷载横向分布影响竖向坐标表
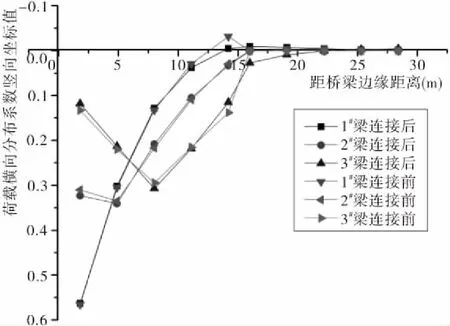
图5 1#~3#梁连接前后的荷载横向分布影响示意图

图6 4#~5#梁连接前后的荷载横向分布影响示意图
2.3 上部结构受力分析
根据公路桥涵设计规范[7],可以得到荷载设计公式(3)。
S=γ0(γGSGk+γQ1ΨC1SQ1k+γQ2ΨC2SQ2k+γQ3ΨC3SQ3k)
(3)
式中,γ0——结构重要性系数,取为1.0;
γG——永久荷载分项系数,取为1.35;
SGk——永久荷载标准值;
γQ1——汽车分布荷载分项系数,取为1.4;
SQ1k——汽车分布荷载标准值,取为10.5 kN/m;
γQ2——集中荷载分项系数,取为1.4;
SQ2k——集中荷载标准值,取为356 kN;
γQ3——人群荷载标准值,取为3.5 kN/m;
SQ3k——人群荷载分项系数,取为1.4;
ΨC i——第i项可变荷载的组合系数,均取为0.7。
在跨中弯矩同号荷载影响线施加荷载,使跨中弯矩达到最大值,采用ANSYS的非线性计算方法,得到上部结构在设计荷载作用下,桥梁的最大位移、最大压应力、最大拉应力,列于表2,1#桥的最大主应力图如图7所示,1#桥、2#桥连接后最大主应力图如图8所示。从图中可以看出,连接前后,各桥的最大位移出现的位置大致相同,且最大位移小于跨度的1/600,最大压应力小于C40混凝土的设计值,符合规范要求;所不同的是,在两桥连接后,最大位移、最大压应力均有所减少,最大压应力和最大拉应力出现的点均出现转移,这是由于横向连接改变了桥梁的受力分布所致,证明两桥间添加横向连接有助于提高桥梁的承载能力。值得注意的是,现实工程中,普通钢筋混凝土桥梁允许少混凝土部分开裂,从表2也可以看出,连接后最大拉应力有所增加,甚至超过了C40混凝土的强度设计值,但是小于其标准值,应该引起设计人员的注意。连接前后,1、2#桥的大节点、小节点处均出现应力集中,数值在15~17 MPa间,连接后应力集中稍微减弱,但仍然在14~16 MPa之间。

表2 刚架拱桥设计荷载作用计算结果表

图7 连接前结构主应力图

图8 连接后结构主应力图
3 动力性能分析
采用ANSYS的模态分析功能对连接前后的刚架拱桥进行动力学分析,得出其固有频率,列于表3。从表中可以看出,连接后的刚架拱桥的前三阶固有频率均比连接前得刚架拱桥大,后三阶固有频率对比规律不明显。实际工程中,桥梁的振型可以看成为各阶振型的组合[8],较低阶的振型占总振型的比重越大,而固有频率越高,则说明需要的条件越多,故越难发生,因而可以知道连接后的钢架拱桥的动力性能有所提高,有助于承载能力的提高[9]。从振型来看,连接前后的前几阶振型变化不大,后几阶振型变化较大,但是由于前两阶振型所占比例很大,故可以说明连接前后桥梁实际振型相差不远。
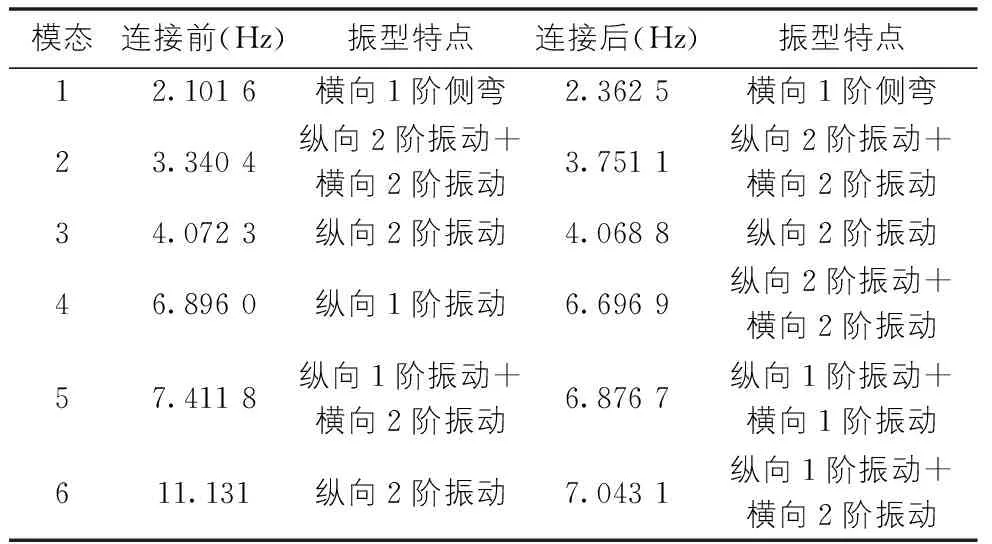
表3 固有频率比较
4 结语
通过建立数值模型,分析得到的数据,对于连接后的刚架拱桥,可以得出以下结论:
(1)边梁的受力情况得到改善,对于类似的工程,建议对两座桥梁进行横向连接;
(2)在设计荷载作用下,挠度和应力符合规范要求,且最大挠度、最大压应力有所减少,桥梁的承载能力得到提高;
(3)桥梁1阶固有频率和2阶固有频率都有所提高,动力性能得到改善。
[1]广东省交通厅.刚架拱桥——清远北江大桥第一版[M].广州:广东科技出版社,1989.
[2]刘云川,刘建民,王志辉.刚架拱桥病害特点与防治对策[J].山东交通学院学报,2006(6):26-28.
[3]童孟胜,卢彭真,张英志.刚架拱桥的病害分析及防治对策[J].科学技术与工程,2004(8):694-698.
[4]杜 斌,聂向珍.简支转连续预应力桥梁的仿真[J].武汉大学学报(工学版),2004,6(3):74-78.
[5]贡金鑫,赵国藩.钢筋混凝土结构考虑耐久性的可靠度研究进展[J].工业建筑,2000(11):528.
[6]刘 华,叶见曙,俞 博,等.桥梁荷载横向分布系数计算方法[J].交通运输工程学报,2009,2(1):62-66.
[7]JTG D60-2015,公路桥涵设计通用规范[S].
[8]刘晶波.结构动力学第一版[M].北京:机械工业出版社,2009.
[9]李远哲.刚架拱桥抗震初步性能分析[D].重庆:重庆交通大学,2010.
