基于MATLAB的汽车换挡性能结构参数优化设计

陈 雷 盛雪莲 孙 云

（常州轻工职业技术学院 江苏 常州 213164）

引言

同步器的同步性能通过同步时间和换挡冲量来评价最为准确[1]。宝马汽车公司的工程师们建立了整车的动力学模型，从整车这个大环境下分析影响换挡性能的因素和如何缩短同步时间[2]。国内汽车巨头公司的研发人员近年来在同步器的结构优化和改进上取得了一定的成绩[3]，不过由于国内的机械加工行业加工工艺水平的缺陷，有时无法实现结构改进的研究成果，国内材料学的研究进展也很局限[4]。

本文以某款变速器的同步器开发为契机，用UG建立三维模型，将模型导入ADAMS并建立多体系统动力学模型，利用MATLAB编程以缩短同步时间为目的，改变那些对同步时间有影响的部分参数，得到这些参数的最优设计，并且通过正确的仿真模型得到了验证[5]。

1 换挡性能结构参数

锁止角是影响同步器换挡性能的关键结构参数之一。在同步之前，为了防止脱环引起锁止失败，同步器的摩擦力矩必须大于等于拨环力矩。

式中：MS表示摩擦力矩，Mb表示拨环力矩。进一步化解可得锁止半角β的下限值：

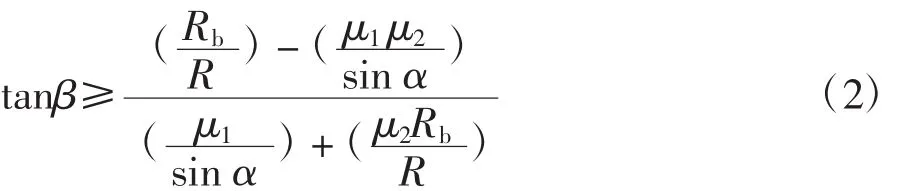
式中：Rb是为同步环花键锁止面平均半径，R是锥面平均半径，即同步半径。μ1是工作锥面间的动摩擦系数，μ2为锁止面间的静摩擦系数。α是锥面半角。值得注意的是同步器锁止条件计算方法仅得出了锁止半角β取值范围的下限值，而未给出其上限。而且在上述计算过程中，未考虑在变速箱内，同步器受到温度和润滑油等因素的影响，锁止面摩擦因数可能下降，这使得计算所得的锁止半角下限值偏小。对于实际设计时，β的取值也是有限制的。当小于下限值时，由公式可以看出，换挡冲击比较大，这样的同步器在长时间使用出现磨损情况下，会导致摩擦系数下降，进而恶性循环，冲击力会更大[6]。

锁止角合理的同步器只需要比较小的换挡力，这样可以减轻车主的用力。一部分生产厂商都是使用普通的机械机床配套专用刀具与夹具来大批量生产同步器。因此生产节拍很快，产品的转换也较频繁。

同步器的摩擦面锥角越小，同步力矩越大。两者属于反比关系，所以为了追求小的同步时间，就需要大的同步力矩，进而需要小的摩擦锥面角。但摩擦锥不能盲目的减小，摩擦锥角小于临界值会造成同步器的摩擦锥面抱死。总的来说锥面半角α的取值范围如式（3）所示。

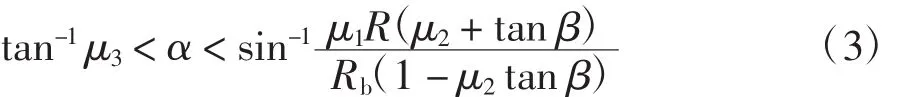
式中：μ3表示锥面的静摩擦系数，其余各个量的含义上文可以查到，这里就不再一一赘述了。在实际的生产过程中，考虑摩擦过程中热膨胀作用会使同步环脱锁困难的影响因素，应该在半锥角取值范围之内取稍大的半锥角值，这样不仅满足锁止条件和防止同步环抱死，而且产生二次冲击最小，改善换挡性能，延长了同步器使用寿命[7]。

2 参数优化设计

2.1 5个变量

同步器的设计参数有很多，这里选取5个具有代表性的参数作为设计变量。同步环锁止面锁止半径Rb，锥面平均半径R，锥面半角α，锥面工作宽度b，锁止半角β。其形式为：[X1 X2 X3 X4 X5]=[RbR α b β]。

2.2 线性与非线性约束条件

首先，同步环工作面宽度是有一定限制的，为了限制它的尺寸，可以和同步环的锥面平均半径作比较。如公式（4）所示。

该公式确定了线性不等式的约束条件，由于选取的5个变量不涉及线性等式的约束，所以线性等式约束可以置为空。其次，非线性等式与不等式的约束。摩擦锥面所能承受的强度是一定的，由公式（5）可知：

式中：NP为锥面单位面积上所承受的压力，由于是锥面，各处半径不同。所以采用平均半径近似计算，R为锥面平均半径，b为锥面宽度，[N]为比压许用值。

对于锁止面的锁止角也有限制，可参考前文理论分析得到的锁止角下限值公式（2），由于锥面动摩擦系数μ1比较小，在编程中可以简化为公式（6）：

式中：μ2为锁止面静摩擦系数，β为锁止半角，α为锥面半角，Rb为锁止面平均半径。

锥面半径α的限制主要在于防止锥面自锁，进而确定了α的下限值，如公式（7）所示。

由于没有非线性等式约束，可以都置为零。

最后，确定同步器主程序编写中的5个变量上下限和初始值。对于锁止面平均半径可以取在85～92 mm之间，锥面平均半径取在65～75 mm之间，锥面半角取在6°～7°之间，锥面宽度选在13 mm～22 mm之间，锁止半角选在50°～60°之间，初始值可以选用该款变速箱三、四挡同步器设计参数[8]。

2.3 同步时间目标函数

本文编程优化设计目标在于缩短同步时间，可以用同步时间为目标函数。如公式（8）所示。

2.4MATLAB主程序

使用matlab自带工具箱中的优化函数fmincon来编辑主程序，将目标函数程序、约束条件程序分别编辑。需要注意的是在编辑程序时，单位要换算一致。图1为主程序内容。

在myfun中编辑目标函数表达式，在mycon中编辑约束条件。最终运行结果如图2所示。

图1 matlab主程序

图2 程序运行结果

由图2结果可以知道，fval为最终的最优值，为0.290 4 s。x为取得最优解时所对应的变量值，此时同步环锁止面的平均半径为88 mm，同步环锥面的平均半径为75 mm，锥面半锥角为6.2773°，锥面宽度为16.666 7 mm，锁止半角为55°，exitflag等于1，表示此时函数收敛[9]。

3 模型重构与验证

3．1 第一次模型的建立

一个完整的adams模型建立过程：首先对模型中的各个部件设置转动惯量，在部件之间添加运动副；其次接触的添加与设置是仿真成功与否的关键所在；最后就是添加驱动和单向力。最终导入adams并设置好初始状态后的同步器模型如图3所示。

对该模型进行仿真分析，结果如图4所示。

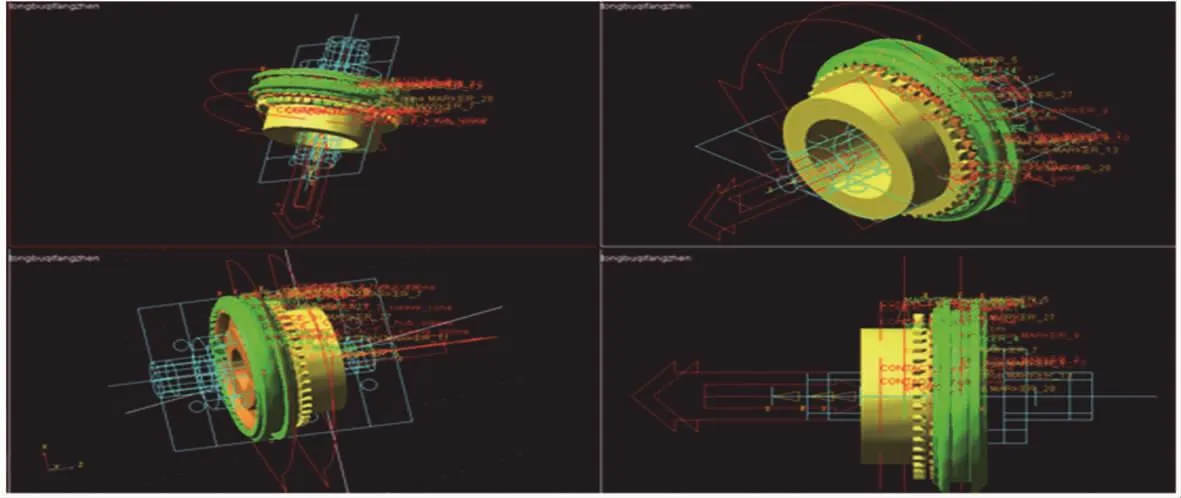
图3 加载好约束后的adams同步器模型

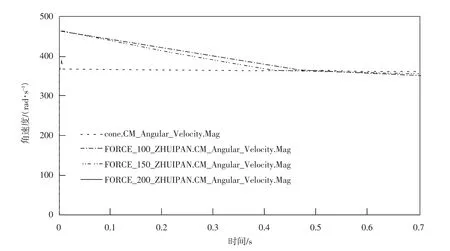
图4 优化前的同步时间

3.2 重构模型与模型的验证

按照本文第二部分参数优化设计得到的最优解对应的变量值，将锥面平均半径增大3 mm，锥面半角可以取整数，在原来基础上减小到6.3°，锥面宽度增大0.6 mm，锁止角保持不变。按照以上的一组数据去修改同步器UG模型的同步环，修改同步环零件后，UG的装配模型会自动更新，将该模型再重新导入ADAMS中，添加约束、接触等，设置仿真时间为0.7 s，步数为500步，开始仿真，最终的结果曲线图如图5所示。

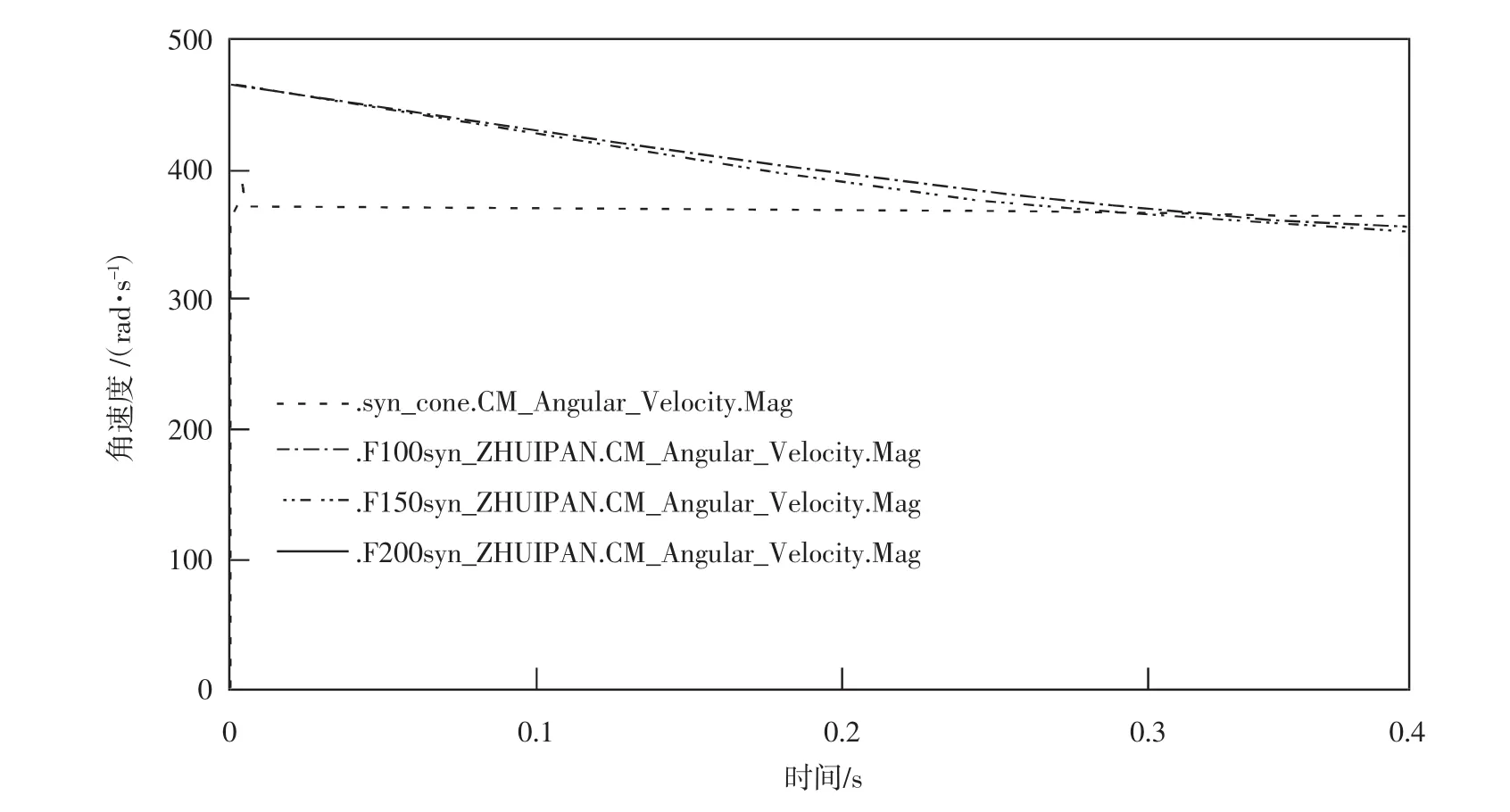
图5 优化后的同步时间

syn_ZHUIPAN.CM_Angular_Velocity.Mag表示接合齿圈的角速度变化曲线，其他3条曲线F100，F150，F200分别是 100 N，150 N，200 N 这 3种情况下接合齿圈的角速度变化曲线。由图5结果分析可知，按照优化程序求出的解去重新构建模型后，3种不同换挡力大小作用下的结果相比图4的同步时间都缩短了0.12 s左右，现在落在0.3 s～0.33 s之间，同步时间是准确可信的，仍然是换挡力越大，同步时间越小，符合同步器理论，优化后的模型正确性得到了验证。

4 结论

图4所对应的没有使用优化参数构建的同步器模型，该模型同步时间都落在0.43～0.46 s之间。优化后的同步器模型同步时间如图5所示，现在落在0.3～0.33 s之间。所以优化以后的同步器模型同步时间相比优化之前的缩短了20%～30%。

本文的matlab程序优化是以同步时间作为单目标函数，以后的研究工作者可以考虑以同步时间和换挡冲击力两者作为双目标函数，在缩短同步时间的同时也兼顾减小换挡冲击力。

1 张福龙.基于虚拟样机技术的汽车变速器换挡性能研究[D].上海：上海工程技术大学，2013

2 徐向阳，傅艳晓.国外汽车传动技术的一些最新发展[J].汽车工程学报，2013（4）：235-241

3 兰丽辉.关于CAD产品的参数化设计方法的探讨[J].长春工程学院学报（自然科学版），2003（3）：70-72

4 Hiroaki H.Simulation on synchronization mechanism of transmission gearbox[C].International ADAMS User Conference,1998

5 易园园.AMT换挡机构动态仿真与优化设计[D].广州：广东工业大学，2014

6 张佳楫.含间隙机构运动副动力学模型研究[D].西安：西安电子科技大学，2006

7 杨子发.轿车操纵稳定性的虚拟样机分析与试验研究[D].长春：吉林大学，2006

8 王颖，郭永洪，李梅，等.基于MATLAB的小电流接地系统简单故障仿真实验[J].高校实验室工作研究，2013（3）：32-35

9 Peter Kovesi.MATLAB and Octave functions for computer vision and image processing[J].Digital Image Computing：Techniques and Applications，2012：101-107