基于RSSI测距修正的无线传感器网络四边形加权质心定位

，，

(广东工业大学 自动化学院，广州 510900)

0 引言

无线传感器网络(wireless sensor network，WSN)是由大量低功耗，多功能，低成本的传感器节点组成的网络，该网络具有环境适应性强、自组织能力和组网成本低等特点[1]。WSN由于其广泛的实际应用而在当今世界中引起极大关注，实用性可以从远程导航系统和紧急服务定位到工业的一氧化碳检测[2]和社区人群的定位，跟踪[3]。除了紧急情况和导航之外，常见的应用还有军事侦察与监控、环境信息监测、宇宙空间的探测和应急救援救灾等前沿领域[4]。然而，实现小功率、低成本和高精度的稳定定位仍然是WSN领域研究的热点[5]。

根据是否需要测距，WSN定位算法可分为两类：距离相关(Range-Based)和距离无关(Range-Free)的定位算法[6]。其中Range-Free定位算法定位精度不高，不能满足高精度应用的要求；Range-Based定位算法定位精度较高，但需要较高的硬件条件。常见的测距方法有接收信号强度指示(RSSI) 、到达时间TOA(time different of arrival)、到达时间差TDOA(time of arrive)和到达角度AOA(angle of arrive)等。其中，后3种方法需要额外的硬件条件，结构比较复杂，成本也比较高[7]。由于节点本身具有无线发射功能，对信号强度的测量也容易实现，因此作为一种低成本、低复杂度的测距方案受到国内外学者的广泛关注。其缺点是无线信号的传输容易受外界环境(障碍物遮挡、多径效应和噪声等)因素影响，加上本身信道衰落，导致RSSI测量存在较大的误差[8-9]。因此通常需要采取相应算法来提高测量精度，如设计相应的滤波器或对测量值进行加权等方法[10]。

近年来的相关文献已经提出各种方法来解决定位问题，但这些算法各有利弊，对于不同的应用，没有统一的解决方案，只是针对定位的某个阶段进行改进，定位效果有待进一步提升。文献[11]用高斯滤波器过滤波动大的RSSI值，并对过滤后的RSSI值进行加权计算，降低了测距误差，但在加权计算的时候没有考虑RSSI值刚好等于均值的情况；文献[12-13]中根据未知节点接收信号的强度赋予参与定位的锚节点不同权重；文献[14]利用4个锚节点，每3个为一组进行四次定位，再对4个定位点进行加权计算，最后确定未知节点的位置，使定位更加精确。文献[15]提出了一种基于RSSI测距的多级能量定位算法，降低了定位的误差。但文献[12-15]均没有考虑在测距阶段RSSI值受环境的影响会产生较大的误差，直接影响定位结果的精确性；文献[16]选择根轴相交组成的区域作为定位参考区域，将该区域的质心作为未知节点的位置，但假设的是特殊情况下的模型，在实际中很难应用。文献[17]假定理想的部署条件来测量距离的传感器节点，即该定位方案，所有节点都部署在固定的距离为3～8米，但在现实很多应用中，节点都是随机部署的。文献[18]提出一种半分布式的定位机制，未知节点通过接收一定区域的锚节点来估计位置，这些完成定位的节点升级为锚节点来参与定位其它未知节点，该算法属于粗定位，虽然提高了节点的定位成功率，但容易造成误差累积，定位精度难以保证；文献[19]提出基于时间的定位算法，原理类似TOA算法，该算法的优势在于不需要时间同步就能获得节点间的距离。但需要很详细的时间划分，增加了该算法的计算复杂度。

针对上述问题，本文提出基于RSSI测距修正的四边形加权质心定位算法。首先在高斯滤波的基础上，对高斯滤波后的RSSI值进行中值加权计算，让最终得到的RSSI值更加接近真实值；其次，使用四边形加权质心定位算法来计算未知节点的位置，并设计更加符合四边形加权质心的权值，对于交叉区域的每一个内侧交点，其权值由锚节点与未知节点的测量距离之和的倒数作为权值。最后仿真实验表明，定位精度得到了提高并且表现更好的稳定性。

1 无线信号传播模型

本文主要采用对数正态阴影模型，即Shadowing模型，该模型是目前应用较多的一种测距模型，它考虑了实际环境的复杂性[20]。如公式(2)所示：

(2)

在式(2)中，PL(d)为距发射端d处的路径损耗，单位是dB；PL(d0)为距发射端d0处的路径损耗；d0通常取为1；k为无线信号的衰减因子，一般取2到4；Xσ为高斯分布，其均值为0，方差为σ2。

由于节点接收信号强度指示是功率，把式(2)两边分别取对数可得：

RSSI(d)=A-10klgd+Xσ

(3)

在式(3)中，A=10lgPr(do)表示信号传播d0时的接受功率,则接收端与发送端的距离可以通过式(4)获得:

(4)

2 加权质心定位介绍

质心算法(Centriod Algorithm)是一种利用网络连通来定位,通过与未知节点通信的锚节点所组成多边形区域的质心作为未知节点坐标[21],算法如图1所示。

图1 质心算法原理图

假设A，B，C，D，E分为未知节点M通信范围内的5个锚节点，其坐标分别为(x1,y1)，(x2,y2)，(x3,y3)，(x4,y4)，(x5,y5)，则未知节点的估计坐标为：

一些研究者对其进行了改进，利用了测距信息。通过权值来反映不同锚节点对未知节点的影响程度[22]。假设无线传感器网络中有未知节点的坐标为D(x,y)和n个锚节点坐标分别为(x1,y1), (x2,y2),…(xn,yn)，则加权质心定位算法的公式如(5)所示：

(5)

在式(5)中，ωi表示第i个锚节点的权值，ωi为未知节点与第i个锚节点的距离的倒数。

3 本文定位算法

3.1 高斯加权滤波算法

在实际测量中，在短时间内未知节点收到n个RSSI值，由于外界环境的影响，这些RSSI值具有很大的波动，但总体上呈现出高斯分布[23]，如图2所示。

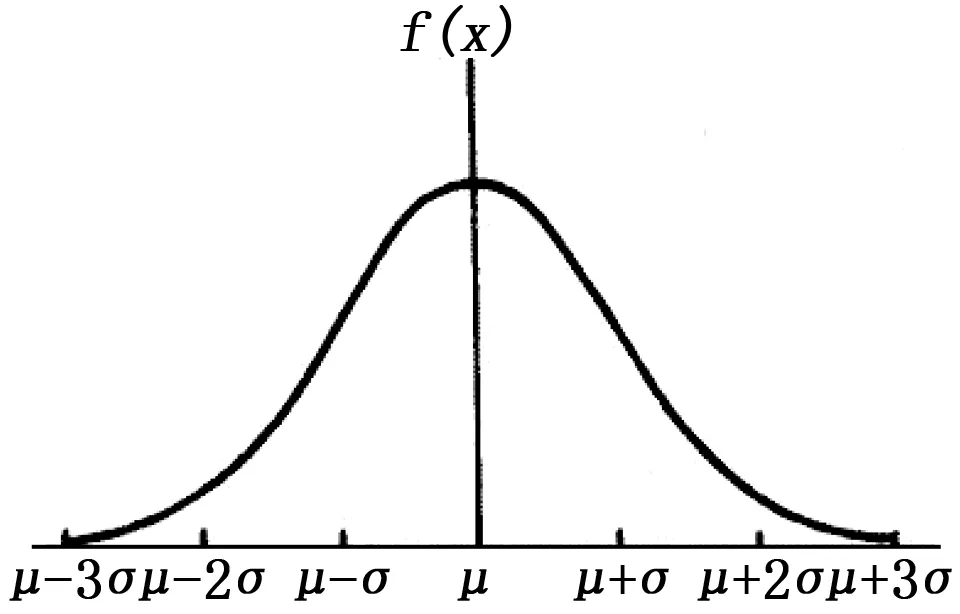
图2 高斯分布曲线图

单纯的均值滤波和中值滤波对数据处理存在较大的误差，而高斯滤波虽然去除了波动大的值，但剩下的RSSI数据是仍然是波动的，本文采用高斯加权滤波对RSSI值进行修正，其核心思想是：先采用高斯滤波器剔除波动大的值，接着使用中值加权方法对滤波后的RSSI值进行校正得到最终的RSSI值。该算法能有效地减少小概率、大干扰对整体测量数据的影响，也能充分利用剩下RSSI值的信息，让最终的RSSI值更加接近真实值。此方法具有稳定性和适用性，更加适用于复杂的环境。加权高斯修正RSSI值的步骤如下：

1) 对RSSI值进行高斯滤波。高斯函数如公式(6)所示，在锚节点广播信号完成之后，计算出每组RSSI测量值的参数μ和σ，并且事先设定一个测量误差的门限阈值K，若f(RSSIi)>k，则表示误差值超出范围需要剔除，并置其权值λ为0;否则，权值为1。本文确定误差门限值的原则是：选择概率较高的区域，高概率发生区，由高斯分布函数性质可知位于区间(μ-σ，μ+σ)内的面积占总面积的68%，而一般只需要选择概率大于0.6即可[24]。

(6)

2)对高斯滤波后剩下n个信号值(RSSI1,RSSI2，…，RSSIn)，对其按数值大小进行排序，并找出中值RSSIm，RSSIm的值由公式(7)确定。

(7)

求出各个RSSI信号强度与中值RSSIm的差，如公式(8)所示：

Di=(RSSIi-RSSIm)

(8)

考虑到过滤后的信号值刚好与中值相等的情况，用公式(9)来表示加权系数：

(9)

进行权值系数归一化处理，如公式(10)所示：

(10)

其中:RSSIi第i个RSSI值，可以看出RSSIi和RSSIm相差越大，相对应的加权系数越小；反之，则越大；当RSSIi和RSSIm相等时，加权系数最大。

3) 把高斯过滤后的信号值与其相应的权值相乘，再对它们进行求和，得到的结果作为优化后的RSSIopt值，公式如下：

(11)

3.2 四边形质心定位算法

由于外界环境的影响，锚节点本身有可能出现自身的定位精度误差大，比如在森林中，锚节点域受树荫的遮挡，有些锚节点自身的精度可能高达15米[25]，有时候锚节点因潮湿等因素造成损坏而无法定位，导致定位阶段误差大。因此，采用四边形来计算未知节点的坐标，具体方法是：首先把最优RSSI值转化成距离，然后找出最近4个锚节点，并以其坐标为圆心，距离为半径画圆，如图3所示。四边形区域是由相邻两圆交点的内侧坐标所组成，用加权质心算法计算该区域的质心并作为未知节点的坐标。其权值的选择依据是内侧的每一个交点由两个相邻的锚节点与未知节点的测量距离共同决定的，如公式(12)所示：

(12)

其中:d1，d2，d3，d4分别为未知节点到各个锚节点A，B，C，D的估计距离，E，F，G，H为内侧4个交点，其坐标为(x1，y1)，(x2，y2)，(x3，y3)，(x4，y4)其中第i个内侧交点坐标对应的权值为其相邻两个锚节点与未知节点的测量距离之和的倒数，N为未知节点的坐标。

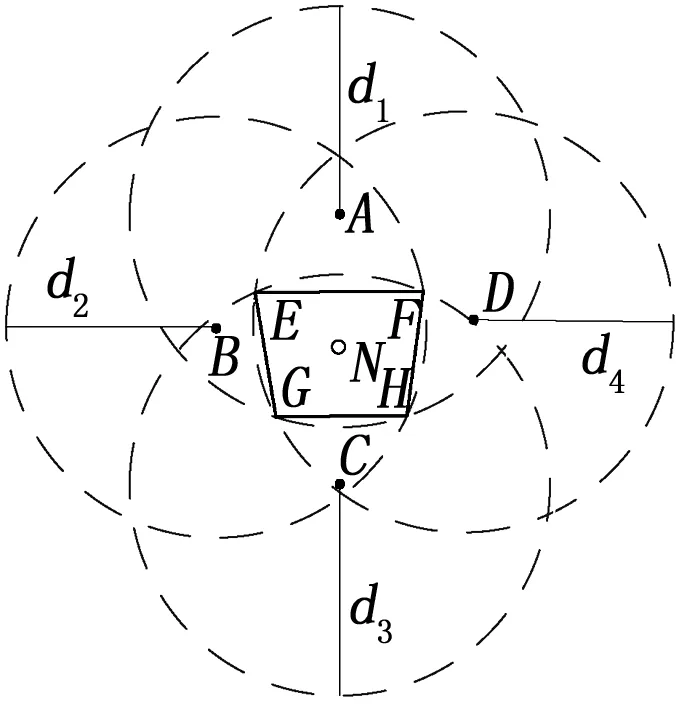
图3 四边形加权质心定位算法

如图所示，越多的锚节点参与未知节点位置计算时，其相交得到的区域会越小，定位精度会越高；但在实际应用中锚节点容易受环境影响出现定位精度低或者无法定位的情况，本文提出的定位算法其鲁棒性明显优于传统的三角形加权质心定位算法；然而并不是一味的增加锚节点参与定位的数量就是可行的，四边形质心算法在内侧交点的选择方式和三角形质心算法的方式不太一样，最近的4个锚节点A，B，C，D在计算内侧坐标的时候是选择两两相邻圆的内侧交点，比如以A和C为圆心的两个圆是不相邻的，两个交点都不属于内侧的。其核心思想是判断哪些锚节点是两两相邻(即对锚节点进行逆时针或者顺时针判断)。假设我们事先不知道选择4个锚节点的顺序，随机选择两个锚节点B和C的坐标，由两点确定一条直线可得出直线方程为F(x)=kx+b，并把另外两个锚节点A和D的坐标(xi,yi)和(xj,yj)代入该直线方程F(x)并通过公式(13)判断另外两个锚节点是否同侧还是异侧。在判断哪些锚节点是两两相邻的时候会遇到3种情况：1) 另外的两个锚节点的坐标位于直线的异侧。则这两个锚节点的连线是4个锚节点所组成四边形的对角线，那么另外两个也是四边形的对角线，经过一次判断就可以得出哪些锚节点是两两相邻的，如图4(a)所示;2) 如果第一次判断是同侧，则需要再进行一次判断，保持前面随机选择的两个锚节点的其中一个坐标，再选择另一个坐标进行判断，如果两次判断的结果都是同侧，那么这3个锚节点刚好就是所组成四边形的两条边，可以得出哪些锚节点是组成四边形的对角线，也同样可以得到第一种情况的结果，如图4(b)所示;3)如果第二次是异侧，则两个锚节点是组成四边形的一条边和一条对角线，也可以得到第一种情况的结果。如图4(c)所示。

(13)

由上面的分析可知，如果参与未知节点位置计算的锚节点的数目多于4个的话，内侧交点会出现很多个，在内侧交点的选择和判断锚节点的相邻情况的难度和复杂度也会变得很大，计算量也很大。

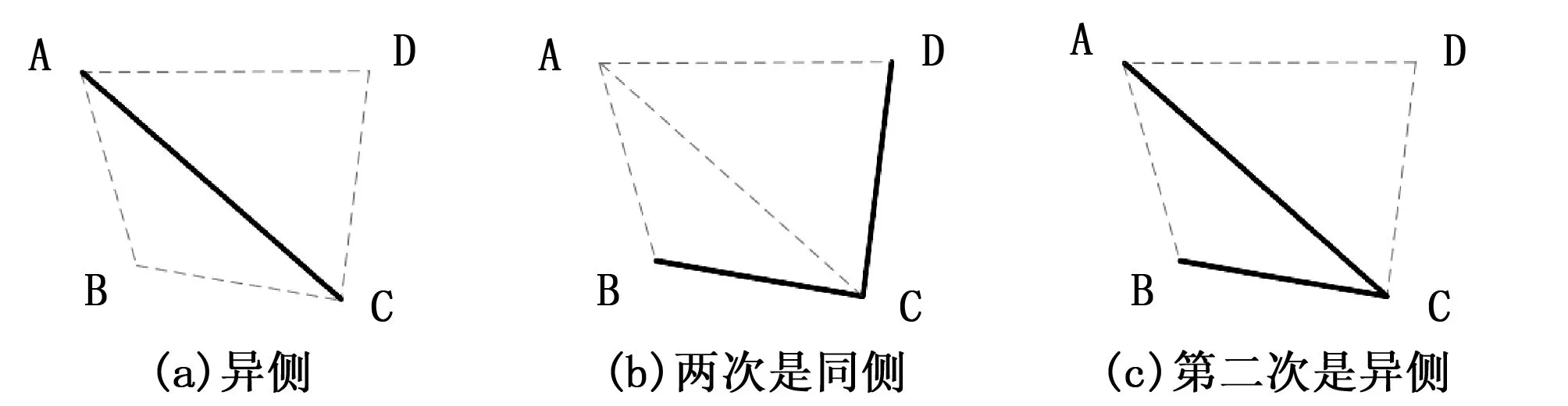
图4 判断锚节点相邻时的3种情况

4 定位算法描述

本文定位算法的步骤如下：

Step 1：锚节点周期性向周围广播信息(ID、位置信息和发射功率)；

Step 2：当未知节点接收通信范围内同一锚数据包达到一定阈值时，对接收到的 RSSI值进行高斯加权处理，得到最优RSSI值；

Step 3：将高斯加权滤波后的RSSI值转换成距离；

Step 4：与未知节点通信的锚节点数目如果大于3个，则执行步骤5；否则用RSSI三角形加权质心求未知节点的坐标；

Step 5：对距离值从小到大排序，选择前4个距离值, 并记录其对应锚节点的坐标；

Step 6：判断哪些锚节点是两两相邻的，并求以两两相邻的锚节点为圆心，测量距离为半径的圆的内侧交点，并计算相应的权值。

Step 7：利用加权质心算法计算内测4个交点所组成四边形区域的质心，并作为未知节点的估计位置并计算和实际位置的偏移误差；

定位算法流程如图5所示。

图5 定位算法流程图

5 仿真分析

评估定位算法标准的主要参数是平均定位误差[26]，如公式(14)所示：

(14)

其中:(xest，yest)为估计坐标，(xi，yi)为实际坐标，R表示节点的通信半径，M表示未知节点的个数。

本文使用Matlab2010a对算法进行仿真，未知节点和锚节点的个数分别为80和20，随机分布在100 m×100 m的正方形区域内。在衰减模型中添加高斯随机变量，试验中假设各次测量相互独立且同分布，即服从均值为零、方差为σ2的高斯分布，用来模拟实际的气候、多径和阴影衰落等环境，衰减系数，n的值取为2，按上述算法和步骤进行仿真。

为了清晰地反应高斯加权滤波算法修正RSSI值后对定位精度的影响，对高斯加权和不采用高斯加权修正所得到的各个节点定位误差进行仿真比较，其中未知节点和锚节点的数目分别为30和20，仿真结果如图6所示。

图6 修正前后误差对比

由图6可知，采用高斯加权滤波算法修正后，每个节点的定位误差均减小了，而且不同节点的误差也比较稳定。

对未知节点的估计位置进行仿真。在默认参数下进行仿真。未知节点的个数为80，锚节点的个数为20，通信半径为30 m，仿真结果如图7所示。

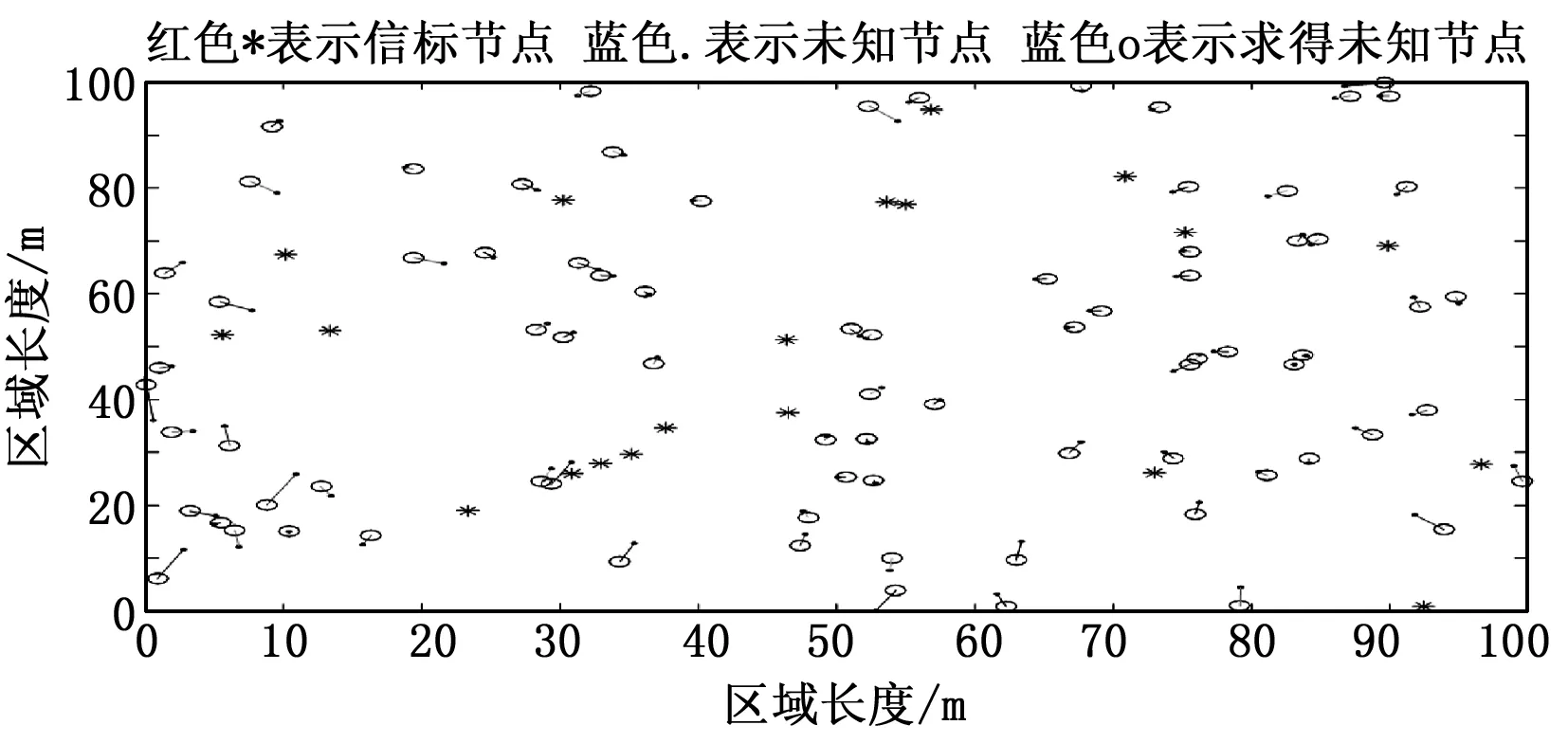
图7 未知节点的位置坐标

由图7可知，锚节点分布比较密集的区域，未知节点的误差线会比较短；较稀疏的区域，误差线会比较长。

不同锚节点数目下的平均定位误差。改变锚节点的数量，分别取为10，15，20，25，30，35，40，45，50通信半径为30 m，分别对质心算法、传统的RSSI定位算法、文献[11]定位算法以及本文提出的定位方法进行仿真比较。仿真结果如图8所示。

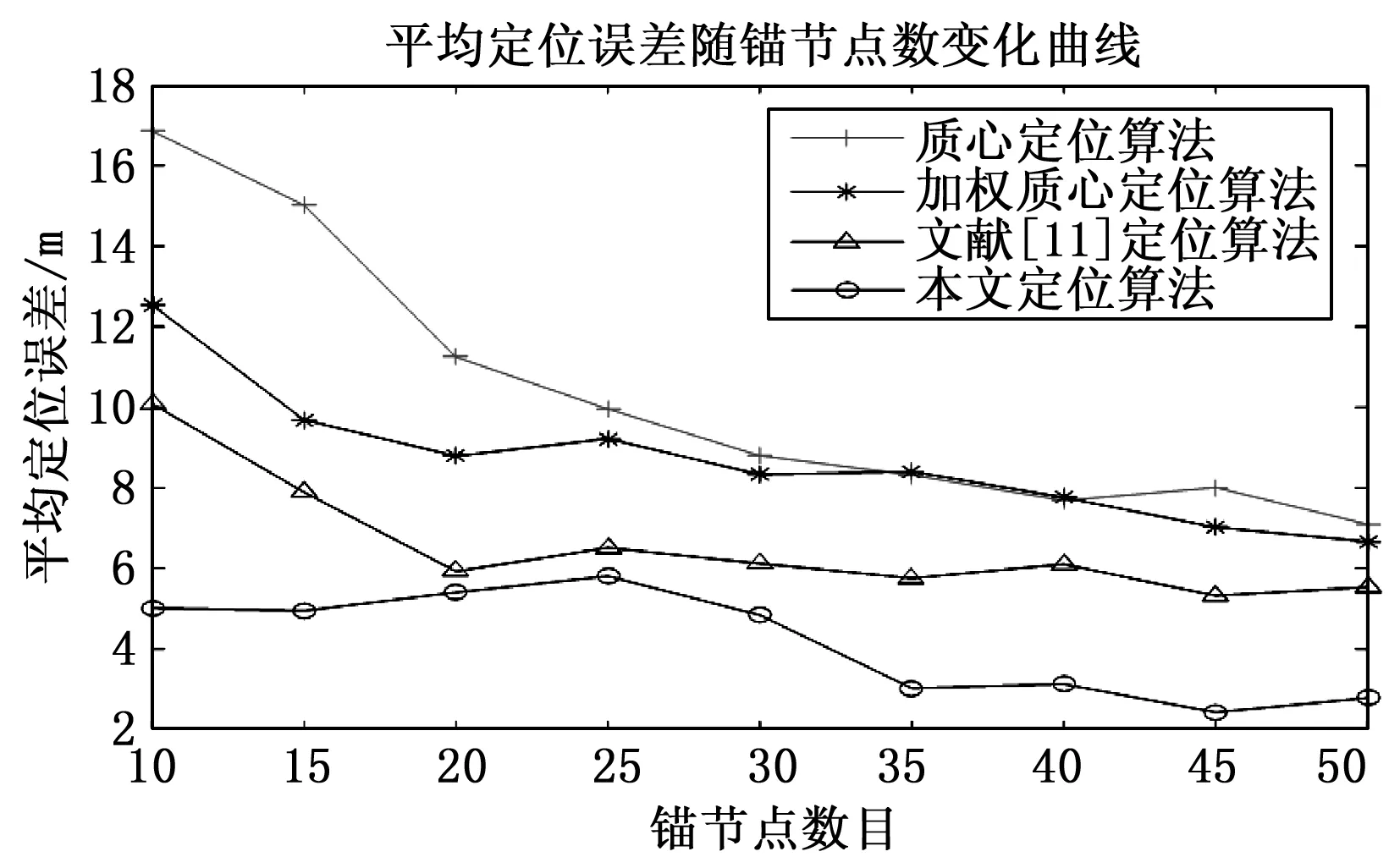
图8 不同锚节点数目下的平均定位误差

由图8可以看出，随锚节点个数从10变化到50，本文定位算法的平均误差都保持最小，4种定位算法的平均误差均有逐渐减小的趋势；在锚节点较少的情况下，本文算法的定位精度优于其它3种，并且随锚节点数目的变化，本文的定位算法更为稳定，当锚节点个数为10时，本文的定位精度相当文献[11]定位算法在锚节点数量为20以上的定位精度，由此也可知本文定位算法不需要大量锚节点来保证精度，减少锚节点数目对于传感器在实际中的应用有着重要作用。

6 结论

本文采用高斯加权滤波得到校正RSSI值，在一定程度上减少了环境对测距结果的影响，提高了测距的精度。使用四边形加权质心定位，降低单个锚节点的权重，提高了定位精度，具有较好的鲁棒性，仿真结果表明本文定位算法在精度、稳定性都优于相比较的3种定位算法。如何利用数据融合技术把不同传感器测距得到的数据进行融合来提高定位精度将是下一步研究工作的重点。

参考文献：

[1] 孙利民,李建中,陈 渝.无线传感器网络[M].北京:清华大学出版社, 2005.

[2] Yang J, Zhou J, Lv Z, et al. A Real-Time Monitoring System of Industry Carbon Monoxide Based on Wireless Sensor Networks[J].Sensors, 2015, 15(11):29535-29546.

[3] Li S, Qin Z, H. Song, A temporal-spatial method for group detection, locating and tracking[J]. IEEE Access, 2016, 1-10.

[4] Kushki A, Plataniotis K N, Venetsanopoulos A N. Intelligent Dynamic Radio Tracking in Indoor Wireless Local Area Networks[J]. IEEE Transactions on Mobile Computing, 2010, 9(3):405-419.

[5] Elkin C, Kumarasiri R, Rawat D B, et al. Localization in wireless sensor networks: A Dempster-Shafer evidence theoretical approach[J]. Ad Hoc Networks, 2016, 54:30-41.

[6] 张新荣,熊伟丽,徐保国.采用RSSI模型的无线传感器网络协作定位算法[J]. 电子测量与仪器学报, 2016, 30(7):1008-1015.

[7] 方 震,赵 湛,郭 鹏,等.基于RSSI测距分析[J].传感技术学报,2007, 20(11):2526-2530.

[8] Li F M, Han P, Luo T. Adaptive area location algorithm combining with packet lost rate and RSSI in wireless sensor networks [J] . Journal on Communications, 2009.30.

[9] 沈 田,温 斌.基于RSSI距离区间映射的加权质心定位算法[J].电子测量技术, 2015, 38(5):42-44.

[10] 文春武,宋 杰,姚家振.基于RSSI校正的无线传感器网络定位算法[J].传感器与微系统, 2014, 33(12):134-136.

[11] 王洪元,蒋燕蓉,焦筱悛,等.一种改进的加权质心自定位算法[J].计算机与应用化学, 2014, 31(3).

[12] 李文辰,张 雷.无线传感器网络加权质心定位算法研究[J].计算机仿真,2013, 30(2):191-194.

[13] 朱忠记,何熊熊,章晓,等.基于RSSI的四边测距改进加权质心定位算法[J]. 杭州电子科技大学学报, 2014(1):17-20.

[14] 李卫东,郭 鹏,侯丽虹.基于RSSI的改进质心定位算法[J].电子测量技术, 2017, 40(1):180-183.

[15] Fang J Y, Chu H C, Jan R H, et al. A multiple power-level approach for wireless sensor network positioning[J]. Computer Networks the International Journal of Computer & Telecommunications Networking, 2008, 52(16):3101-3118.

[16] 方 震,赵 湛,郭 鹏,等.基于RSSI测距分析[J].传感技术学报,2007, 20(11):2526-2530.

[17] Kumar P, Reddy L, Varma S. Distance measurement and error estimation scheme for RSSI based localization in Wireless Sensor Networks[A]. Wireless Communication and Sensor Networks[C]. IEEE, 2010:1-4.

[18] Ghidini G, Pinotti C M, Das S K. A semi-distributed localization protocol for wireless sensor and actor networks[A]. IEEE International Conference on Pervasive Computing and Communications Workshops[C].IEEE, 2010:438-443.

[19] Shah G A, Akan O B. Timing-Based Mobile Sensor Localization in Wireless Sensor and Actor Networks[J]. Mobile Networks and Applications, 2010, 15(5):664-679.

[20] Quan Z, Cui S, Sayed A H. Optimal Linear Cooperation for Spectrum Sensing in Cognitive Radio Networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(1):28-40.

[21] Zhao C, Xu Y, Huang H. Weighted centroid localization based on compressive sensing[J]. Wireless Networks, 2014, 20(6):1527-1540.

[22] Soderstrom T, Stoica P. System identification[M}.London, UK :Prentice-Hall ,1999.

[23] Zhao J, Xi W, He Y, et al. Localization of wireless sensor networks in the wild:pursuit of ranging quality[J]. IEEE/ACM Transactions on Networking, 2013, 21(1):311-323.

[24] Kumar S, Lobiyal D K. Power efficient range-free localization algorithm for wireless sensor networks[J]. Wireless Networks, 2014, 20(4):681-694.

[25] Zhao J, Xi W, He Y, et al. Localization of wireless sensor networks in the wild:pursuit of ranging quality[J]. IEEE/ACM Transactions on Networking, 2013, 21(1):311-323.

[26] Kumar S, Lobiyal D K. Power efficient range-free localization algorithm for wireless sensor networks[J]. Wireless Networks, 2014, 20(4):681-694.