基于改进TOPSIS法的装备维修任务优先级确定方法

2018-04-25，，，，

计算机测量与控制 2018年4期

，，，，

(陆军装甲兵学院技术保障工程系，北京 100072)

0 引言

信息化条件下，装备的打击精度和密度大大提高，战场上短时间内出现大量受损装备，然而维修保障单元数量有限，能在有效的时间内修复的装备数量更是有限。受损装备的受损程度、装备重要程度等属性各不相同，为此依据属性确定受损装备的优先级排序，进行选择性的维修，对保证装备参战率和完好率有着重要意义。

当前装备维修任务的调度主要由装备保障指挥员根据相关装备信息并结合自身知识水平和经验确定，受装备保障指挥员主观因素影响较大，很难确保决策的科学性和合理性。为此，提出一种更加客观的决策方法，构建合理的维修任务优先级评价指标体系，选用合适的评估方法对装备维修任务优先级进行排序。

目前关于优先级的研究已经比较深入。其中，吴云鹤[1]、王震[2]、周培杰[3]等将测控弧段优先级确定问题看作是多目标、多任务的决策优化问题，并分别运用不同的优化算法对目标问题进行研究，给出了优化模型；单晓红[4]运用客观熵权和主观权重相结合的混合权重确定方法对软件企业项目的优先级进行排序，构建评价指标体系并给出了评估过程；李云峰[5]、凌晓东[6]、王磊[7]等人研究了资源优化问题和调度问题下的优先级确定方法。上述研究主要以研究航天测控、企业项目等非军事对象为主，涉及军事方面的大都以研究地空导弹的目标为主，而装备维修任务优先级确定的相关研究很少。

针对战时装备维修任务优先级确定问题，通过分析影响装备维修任务优先级评判的因素构建评价指标体系，并运用马氏距离TOPSIS法进行改进，构建装备维修任务优先级确定模型，最后通过示例计算，检验模型的可行性。

1 装备维修任务优先级描述

装备维修任务的对象是可以由某维修保障单元修复或者后送的受损装备，确定不能处理的受损装备的优先级没有实际意义。所以，在确定装备维修任务优先级之前，必须先对战场上所有装备维修任务进行区分筛选，将本级维修保障单元不能修复或在该时间段内没有维修价值的维修任务剔除，对余下的装备维修任务进行优先级评判。本文中装备维修任务特指战时能由本级维修保障单元修复的装备维修任务，维修保障单元是指具有一定维修能力的本级维修小组。本文将优先级定义为战时装备维修任务在接受维修保障单元维修时的先后顺序。

基于不同维修保障单元计算得出的装备维修任务优先级总是不同的，故装备维修任务的优先级是相对于一个特定维修保障单元进行研究。战时，战场上受损装备不断出现，又不断被修复，故装备维修任务优先级的确定呈现一个动态的过程。并且只有当维修保障单元空闲的时候才会发生，分配相对于该维修保障单元最佳的装备维修任务。

2 装备维修任务优先级确定模型

2.1 问题描述及符号定义

设有m个装备维修任务A1、A2、A3、…、Am，可用n个评价指标B1、B2、B3、…、Bn对各装备维修任务进行评价，运用AHP和改进的TOPSIS法确定各装备维修任务的优先级。

xij表示装备维修任务Ai的优先级评价指标中指标Bj的评价值，由xij构成的矩阵X=(xij)m×n为初始评价矩阵；ωj表示评价指标Bj的权重；C表示初始矩阵X规范化后得到的标准矩阵；E表示标准矩阵C加权后得到的加权标准矩阵；S+表示理想解；S-表示负理想解;Qi表示贴近度；P表示各评价指标的相关系数矩阵。

2.2 基于传统TOPSIS法的装备维修任务优先级确定模型

对于每一个装备维修任务Ai都有n个评价指标Ai=(x11,x12,…,x1j,…,x1n)，由m个装备维修任务的评价指标值组成初始评价矩阵X。

初始评价矩阵X中的各评价值的度量尺度或者单位是不同的，为避免指标之间量纲的影响，对初始评价矩阵X进行规范化处理。规范化处理的方法众多，文献[8]对众多规范化方法进行对比研究，得出向量规范化方法对于利用TOPSIS法研究排序问题最为有效，本文选用向量规范化方法对初始评价矩阵X进行规范化处理。对于极大型指标通过式(1)进行处理；对于极小型指标通过式(2)进行处理。标准化处理后得到标准矩阵C。

(1)

(2)

在标准矩阵C的基础上每列乘以相对应评价指标的权重而得加权标准矩阵E：

E=(eij)m×n=(ωj×cij)m×n=

TOPSIS法的核心思想是判断各备选方案与理想解的距离，根据距离对各备选方案进行排序，得到最优的方案。计算距离之前必须求得理想解和负理想解，对于极大型指标而言依据式(3)进行计算；对于极小型指标而言依据式(4)进行计算。

(3)

(4)

传统的TOPSIS法运用欧氏距离计算各装备维修任务到理想解及负理想解的距离。对于n维变量yi与yj之间的欧式距离计算公式如式(5)所示。

(5)

由欧氏距离计算公式可知受损装备Ai与理想解的欧式距离为：

(6)

受损装备Ai与负理想解的欧式距离为：

(7)

TOPSIS法最终得到的是装备维修任务的一个排序，根据不同装备维修任务与理想解和负理想解之间的欧式距离关系，确定装备维修任务之间的优先级顺序。贴近度是表述两个模糊集之间的接近程度，引入贴近度来表述装备维修任务与理想解和负理想解的接近程度。

Qi=d(ei,S-)/(d(ei,S-)+d(ei,S+))

(8)

由贴近度的表达式(8)可知，贴近度值Qi越大，说明该装备维修任务与理想解越接近，也就是优先级更高。通过各装备维修任务的贴近度可以得到各维修任务的最终排序。

2.3 基于马氏距离的装备维修任务优先级确定模型

马氏距离最早由印度著名统计学家马哈拉诺比斯提出，表示数据的协方差距离。与欧式距离相比，马氏距离的结果能够考虑到各种指标之间的联系，有效避免欧氏距离总是平等对待各种指标而无法满足现实问题需要的不足，并且能够减少指标之间的相关性的干扰[9]。用马氏距离取代传统TOPSIS法中的欧氏距离计算各方案与理想解的距离，能够有效减少评价指标之间的相互影响，使得到的结果更加精确更具说服力。

马氏距离通过引入协方差来判断两个变量之前的关系，变量yi与yj之间的马氏距离计算公式如式(9)所示。

(9)

式中，T-1为变量yi与yj的协方差矩阵的逆矩阵。当协方差矩阵为单位矩阵时，马氏距离计算公式和欧式距离计算公式是相同的。

由于协方差矩阵是通过规范化而消除量纲的影响，所以不需要再对初始评价矩阵进行规范化处理。将权重引入马氏距离计算公式得到受损装备Ai与理想解的马氏距离为：

(10)

受损装备Ai与负理想解的马氏距离为：

(11)

同样，由贴近度表达式(8)计算各维修任务的贴近度，根据贴近度便可得各维修任务优先级的排序。

3 示例分析

以数字化合成营进攻作战中伴随保障为例，维修保障单元在完成一个装备维修任务后，受领下一个任务。此时，数字化合成营的阵地内共有10台受损装备分别用A1、A2、A3、…、A10表示，装备保障指挥员从10台受损装备中选取相对于该维修保障单元优先级最高的作为下一个维修目标。以此为例运用基于马氏距离的装备维修任务优先级确定模型确定10台受损装备的优先级排序。

3.1 评价指标体系的建立及权重的确定

建立装备维修任务优先级评价指标体系是确定其优先级的关键步骤，科学合理的指标体系是确保装备维修任务优先级合理的基础。通过分析进攻作战数字化合成营伴随保障的特点，从装备维修任务、维修保障单元和战场环境三方面入手得出装备维修任务优先级评价指标体系如图1所示。

图1 装备维修任务优先级评价指标体系

受损程度表示受损装备的损伤程度，受损程度均为轻损并用1～5共5个标度分别表示1～5级轻损，标度越大表示受损程度越高；受损装备指作战装备中的受损的作战装备，装备重要程度分为营级指挥车、连级指挥车、排级指挥车、坦克4个等级，分别用标度1～4表示；修复时间指维修保障单元从到达受损装备地点到完成维修所需时间；距离表示维修保障单元到受损装备的实际路程；行驶难易程度指维修保障单元从出发点到受损装备地点之间道路行驶的难易程度，分为难行驶、较难行驶、一般难行驶、较好行驶、好行驶5个等级，分别用标度1～5表示；受敌威胁程度指受损装备所在地受敌军炮火等威胁的程度，分为威胁大、威胁较大、一般威胁、威胁较小和威胁小5个等级，分别用标度1～5表示。

确定维修任务优先级时，需要事先确定各指标的权重，本文选用AHP确定各指标的权重值。依据图1中维修任务优先级评价指标体系，并引入1～9的标度，标度数值越大说明越重要。首先确定B1、B2、B3对A的重要度权重，然后再分别确定第三层指标对第二层要素的权重。根据B1、B2、B3对A的影响程度，利用1～9标度进行两两对比，如表1所示。

表1 第二层指标对目标的重要程度

由表1中0.0171<0.1，可知通过一致性检验。然后根据第三层指标对第二层指标的重要程度确定C11、C12、C13对B1的权重，如表2所示；C31、C32对B3的权重，如表3所示。根据第三层指标对第二层指标的重要程度和第二层指标对目标的重要程度最终确定第三层各指标对于目标的权重，如表4所示。

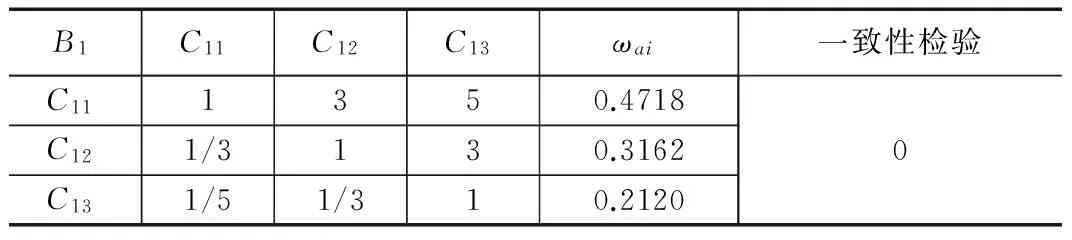
表2 第三层指标对第二层指标的重要程度(1)

由0<0.1，故通过一致性检验。

表3 第三层指标对第二层指标的重要程度(2)

由0<0.1，故通过一致性检验。

表4 第三层各评价指标对目标权重

3.2 两种模型下优先级排序及结果对比

表5 各受损装备受损情况表

表5为各受损装备的受损情况。从表5可以得到对于每台受损装备Ai可以从受损程度、装备重要程度、修复时间、距离、行驶难易程度和受敌威胁程度等6个方面对各受损装备进行表述，将以上数据作为评价该受损装备优先级的初始评价数据，得到初始评价矩阵X。

分别采用传统TOPSIS法和基于马氏距离的TOPSIS法计算各装备维修任务的优先级并排序。

1) 传统TOPSIS法：

为了避免不同评价指标量纲的影响，运用软件Matlab 7.8.0对初始评价矩阵进行规范化处理得到标准矩阵C，并依据表4中各指标权重对标准矩阵C每一列进行加权，进一步得到加权标准矩阵E。

根据式(3)、(4)并运用软件Matlab 7.8.0得出传统TOPSIS法理想解和负理想解分别为S+=(0.1219 0.1051 0.0777 0.1855 0.0572 0.0396)、S-=(0.035 0.0191 0.0198 0.0244 0.0086 0.0133)。

运用Matlab 7.8.0计算各维修任务与理想解、负理想解的欧氏距离如表6所示；由式(8)并运用Matlab 7.8.0计算得出欧氏距离下各维修任务的贴近度如表7所示。

E=(eij)m×n=(ωj×cij)m×n=

贴近度越大的受损装备说明其与理想解越靠近，也就是说贴近度大的维修任务其维修优先级更高。故由贴近度可得各受损装备的优先级为：

。

表6 各维修任务与理想解及负理想解的的欧式距离

受损装备A1A2A3A4A5A6A7A8A9A10d(ei,S+)0.1620.0840.0800.0280.1390.1320.0530.1370.0860.187d(ei,S-)0.1010.1930.1900.2080.1450.1570.2090.1520.1780.088

表7 基于欧氏距离的各维修任务的贴近度

2)基于马氏距离的TOPSIS法:

通常，一个评价指标体系中的评价指标之间很难做到绝对的相互独立，各评价指标之间或多或少都暗含着某种联系，而这种评价指标的冗余对最终的评价结果可能造成不利影响，使得评价结果可信度降低。两个评价指标之间的关联度可以通过计算初始矩阵的相关系数矩阵得出，运用Matlab 7.8.0对任意两个评价指标进行相关系数计算得出相关系数矩阵P。

分析相关系数矩阵P，C11与C13的相关系数达到了0.96，也就是关联度很强，所以传统的TOPSIS法用的欧氏距离不能有效地反映实际重要程度。故本文引入马氏距离代替欧式距离计算不同方案相对于理想解和负理想解的贴近度。马氏距离利用协方差矩阵的特点，能够有效剥离两个指标之间的相互联系。由式(6)、(7)并运用Matlab 7.8.0计算得出各维修任务与理想解、负理想解的马氏距离，如表8所示。

表8 各维修任务与理想解及负理想解的的马氏距离

由表8中数据以及式(8)并运用MATLAB 7.8.0计算可得各受损装备的贴近度如表9所示。

表9 基于马氏距离的各维修任务的贴近度

由表9中基于马氏距离的各维修任务贴近度可得装备维修任务优先级为：A4>A10>A9>A1>A6>A5>A8>A7>A3>A2。

为了证明模型的有效性，现剔除冗余度较高的评价指标“受损程度”，用余下的5个评价指标构建新的评价指标体系，并分别用基于传统TOPSIS法的装备维修任务优先级确定模型和基于马氏距离的装备维修任务优先级确定模型计算10台受损装备的优先级，与原有的结果对比。两个模型计算得出的装备维修任务优先级分别为：A4>A7>A3>A9>A2>A6>A8>A5>A1>A10和A4>A10>A9>A1>A6>A5>A8>A7>A3>A2。

通过分析两个评价指标体系下的优先级评价结果可知：

1)基于传统TOPSIS法的装备维修任务优先级确定模型计算得出的两种评价指标体系下的受损装备的优先级排序是不同的。这说明冗余的评价指标对评价结果造成了影响，同时传统的TOPSIS法不能有效剔除冗余指标对评价结果造成的影响。

2)基于马氏距离的装备维修任务优先级确定模型计算得出的两种评价指标体系下的受损装备的优先级排序是相同的。这说明基于马氏距离的TOPSIS法能够有效的剔除冗余评价指标对评价结果的影响，能够使评价结果更具说服力。

3)对比同一种评价指标体系下不同优先级确定模型得出的受损装备优先级排序发现两个排序差别较大，说明该评价指标体系中评价指标之间的关联度较大(见相关系数矩阵P)。

该维修保障单元此时应该开赴受损装备A4对其进行维修，维修完毕后其他受损装备再按此方法进行计算判断。结果证明该方法能够给出科学的维修任务优先级排序，并具有实际操作性，战时为装备保障指挥员提供科学的决策参考。