五种湍流涡粘模型在二维方柱绕流数值模拟中的对比研究
2018-04-25张显雄张志田张伟峰陈政清
张显雄, 张志田, 张伟峰, 陈政清
(湖南大学 工程试验研究中心, 湖南 长沙 410082)
0 引 言
随着桥梁结构趋向于细、长、柔以及低阻尼方向发展,气动弹性问题成为了大跨度桥梁的控制性因素,因此对各种桥梁抗风问题的研究越来越精细化。计算流体动力学(Computational Fluid Dynamics, CFD)作为一种有可能替代风洞试验的跨学科新型工具,已经在桥梁抗风领域展开了初步应用。相对航天航空、海洋勘探等领域而言,将CFD应用于土木工程面临的一大挑战是:合理的求解结果需要对流体力学基本理论以及有限体积法这一数学工具有较好的掌握,而这正是目前国内的土木工程师所缺乏的。利用CFD对桥梁抗风问题展开研究时,桥梁工程师困惑于如何合理离散网格以及采用哪一种湍流模型展开计算。
国内外众多关于采用CFD进行桥梁抗风研究的文献对各种模拟结果的论述参差不一。就湍流涡粘模型为例,文献[1]采用SSTk-ω湍流模型研究了二维箱梁断面的静气动力问题,得到的气动力系数与大涡模拟值及试验值较一致,这一结果表明SSTk-ω湍流模型可以提供足够的静气动力模拟精度。文献[2]同样采用 SSTk-ω湍流模型对箱梁断面的静气动力问题展开了研究,得出SSTk-ω湍流模型用于二维分析时不能准确预测Strouhal数的结论。对于气动力弹性问题,上述状况同样存在,如文献[3]采用RNGk-ε湍流模型对箱梁断面计算的部分颤振导数与试验数据的相对误差高达100%以上;而文献[4]采用RNGk-ε湍流模型对箱梁断面进行颤振导数计算,却得到了其计算结果能与试验结果吻合良好的结论。当前,虽然已有学者提出了相关建议对CFD计算质量进行评判[5],然而形成统一的检验标准仍然有待发展。
钝体桥梁截面绕流包含多种复杂的流动现象,如剪切层的分离,漩涡脱落与再附,尾流区的发展等。矩形截面柱作为典型的钝体构件,因为具备几何形状简单、分离点固定,流动形态多样等优点,往往被用来验证网格离散方案的适应性与湍流数值模拟的准确性[6-8]。本文选取在桥梁风工程领域应用最广泛的两方程雷诺平均湍流涡粘模型计算方柱(长宽比为1的矩形截面柱)绕流,综合分析了采用五种两方程湍流涡粘模型计算得到的钝体绕流场特性,对各个湍流模型计算结果之间的差异展开了讨论。
1 两方程湍流涡粘模型的基本理论
在桥梁风工程领域,通常认为气体是恒温不可压缩的。通过雷诺平均分解[9](Reynolds Average Navier-Stokes, RANS),可将广义物理量的瞬时值分解为该物理量的时间平均值与脉动值之和:
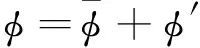
(1)
则可以建立如下的流体基本方程组。
质量方程:
divV=0
(2)
动量方程(Navier-Stokes方程):
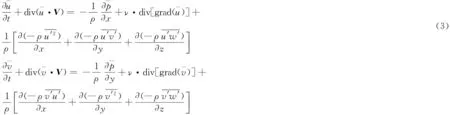
(4)
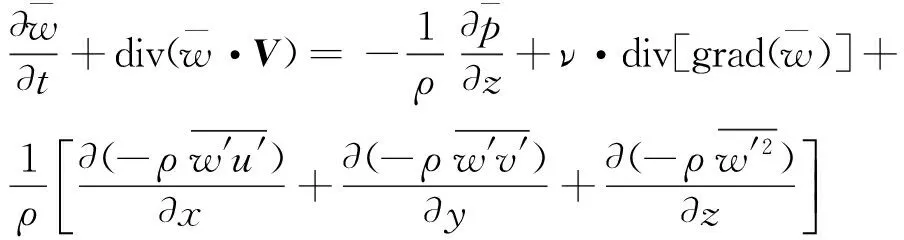
(5)
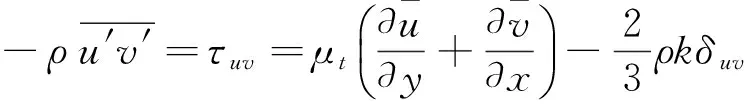
(6)

引入湍流动力粘性系数μt后,6个二阶雷诺应力可以用1个湍动能k表示,于是确定湍流动力粘性系数μt的表达式就成为计算湍流流动的关键。常用的处理法是将μt表征为两个湍流脉动特性参数的函数。所谓两方程湍流涡粘模型是指在流体控制方程组(2)~(5)的基础上引入这两个参数的输运方程,形成封闭的方程组求解流场,其中最典型的是k-ε湍流模型与k-ω湍流模型。
1.1 k-ε湍流涡粘模型
k-ε湍流涡粘模型是一种半经验半理论性的高Re数湍流模型,只适应充分发展的湍流。不同k-ε湍流模型的主要区别在于:1) 湍流动力涡粘系数μt的计算方法;2) 控制湍动能k与湍动能耗散率ε的湍流Prandtl数σk与σε取值;3) 湍动能耗散率ε的生成项与耗散项构成形式。
Standardk-ε湍流模型[10]是最早提出的k-ε湍流模型,其输运方程如下:
Gk-ρε
(7)

(8)
式中,Gk表示根据平均速度梯度计算的湍动能生成项;C1ε与C2ε为常数。湍流动力粘性系数μt的表达式为:
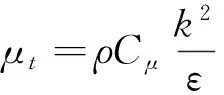
(9)
Cμ为常数,取值为0.09。
由Yakhot与Orzag[11]提出的RNGk-ε湍流模型具有与Standardk-ε湍流模型相似的输运方程:
Gk-ρε
(10)
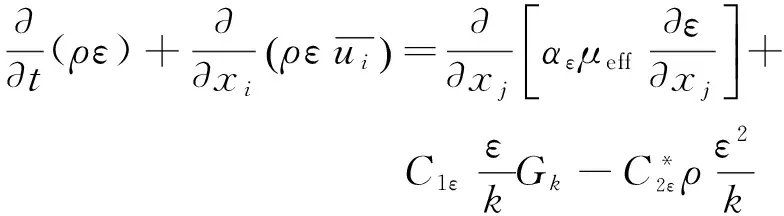
(11)
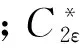
Realizablek-ε湍流模型[12]是比RNGk-ε湍流模型应用更广的一种k-ε湍流模型,Shih在文献[8]中提出湍流动力粘性系数μt的计算与应变率有直接联系,其输运方程发生了明显变化:
Gk-ρε
(12)
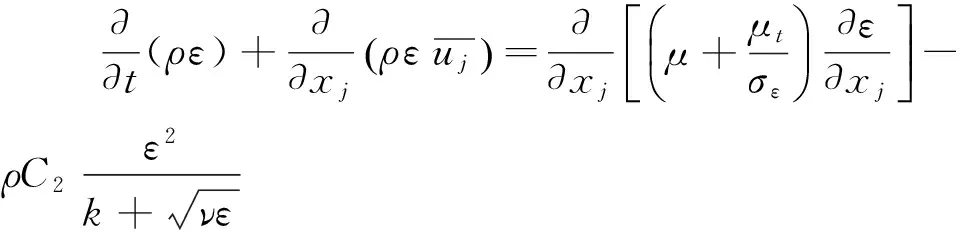
(13)
式中,湍流动力粘性系数μt的表达式依然与式(9)相同,但此时Cμ不再为常数,而是关于k和ε的函数。
1.2 k-ω湍流涡粘模型
基于Wilcox[13]方法改进提出的Standardk-ω湍流模型也是一种半经验湍流模型,ω被定义为特定耗散率。输运方程如下:

(15)
式中,Yk与Yω分别表示因湍流引起的湍动能k以及耗散率ω的耗散项;k与ω的有效扩散系数分别用Γk和Γω表示;Gω代表耗散率ω的生成项,湍流动力粘性系数μt的表达式为:

(16)
α*为降低湍流涡粘性的低雷诺数修正系数,是关于k和ω的函数。
Menter[14]在Standardk-ω湍流模型的基础上进行修正,提出了的分区剪应力输运k-ω湍流模型(SSTk-ω),即在近壁面区域与远壁面区域分别采用Standardk-ε湍流模型与Standardk-ω湍流模型。其输运方程为:

(17)
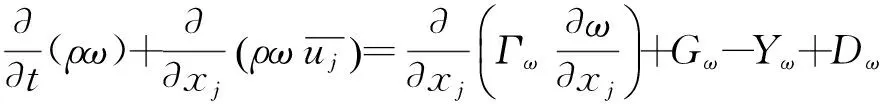
(18)
Dω为交叉扩散项,起协调Standardk-ε湍流模型与standardk-ω湍流模型交界区域的作用。修正后湍流模型的湍流动力粘性系数μt的计算公式为:

(19)
2 模型控制与数值计算
2.1 湍流涡粘模型选取
方柱绕流做为一种典型钝体构件绕流,高Re数下其流动具有固定分离点、尾流区涡旋运动不规则等特性。流体绕经方柱时,流线弯曲,近壁面处流场变化剧烈,方柱表面压力变化迅速;流动在迎风面的角点上分离后,产生旋涡脱落,在尾流区形成自由剪切湍流。方柱绕流因流动现象复杂,物理试验易于实现而被常用来检验湍流模型计算结果的准确程度;另一方面两方程湍流涡粘模型具有形式简单,计算快捷等优点常用来模拟钝体绕流。
本文选取了Standardk-ε、RNGk-ε、Realizablek-ε、Standardk-ω以及SSTk-ω这5个两方程湍流涡粘模型分别模拟方柱绕流场,并结合以往数据,从三分力系数、Strouhal数、回流区长度、脉动力时程特性及尾流区速度场等方面进行综合对比,分析了各个湍流涡粘模型的优劣与差异。
2.2 计算域布置
流体为不可压缩空气,方柱边长D=0.065 m,雷诺数Re=22 000。因为桥梁为大跨高耸结构,展向不同截面处的流动具有一定的相似性,而且展向的流动尺度远小于其余两个方向的流动尺度,因此本文采用二维分析。参照Tamura等的观点[15]将计算域设置为圆形并在全计算域采用对称离散方案,避免网格不均匀加剧数值误差。方柱中心到计算域周边的距离为50D,阻塞率为2%,满足风工程研究的要求[16]。其中计算域入口边界条件为来流速度入口,水平来流速度U=4.95 m/s,来流湍流度0.5%;出口为压力出口边界条件,本文指定出口边界上的压力恒定为0;方柱表面为固壁边界条件。CFD计算域布置如图1所示。
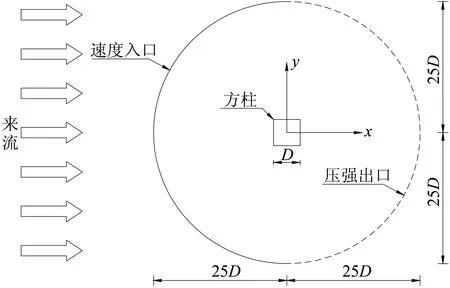
图1 计算域布置方式Fig.1 Arrangement of computational domain
采用结构化网格离散计算域。所有湍流模型在近壁面处采用增强壁面处理方式(Enhanced Wall Treatment,EWT)[17]考虑边界层效应,保证不同的湍流模型可以采用相同的离散方案。本文分别采用了5种离散方案,各离散方案的网格数呈倍数增加,详细的离散方案见表1。
以离散方案三为例,方柱近壁处网格划分图2所示。

表1 网格离散参数Table 1 Parameters of discretization

图2 方柱近壁处网格Fig.2 Grid near the square cylinder
本文在计算域内布置了226个测点用来监测不同湍流模型下的方柱绕流特性。在尾流区离方柱0.5D、1D、2D、3D、5D、8D的六个剖面位置处各自沿Y方向均匀布置了17个测点,测点编号为1~102;在尾流区流向中心线上,均匀布置76个测点,测点编号为103~178,用来监测尾流区的速度场。为获得方柱表面的非定常压力脉动,本文在方柱各边均匀布置48个压力监测点,测点布置与编号如图3所示。根据有限体积法(Finite Volume Method,FVM)计算原理,文章在四个角点位置处(P179,P191,P203,P215)设置测点的计算结果并不具备数学意义,只是用来标明各侧面的长度界限。
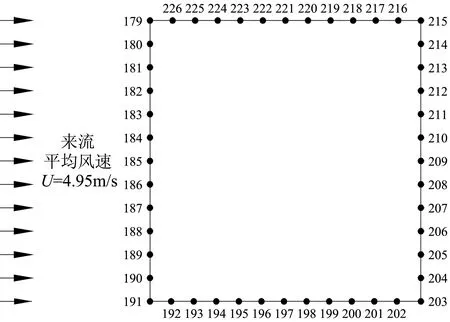
图3 方柱表面压力测点布置图Fig.3 Gaging point of static pressure
2.3 数值方法控制
对于高Re数下的方柱绕流,本文采用二阶隐式格式对流体控制方程的瞬态项进行离散,空间离散采用二阶迎风格式;压力与速度耦合方程采用扭曲修正率为1的SIMPLEC隐式方法进行解耦;根据以往报道数据,雷诺数Re=22000时方柱涡脱频率约为9.5 Hz~10.5 Hz,计算抽样频率取涡脱频率的200倍,符合采样定理的要求;无量纲时间步长T=UΔt/D设置为0.0381;每一时间步长内迭代20次或者当流体控制方程的各项残差小于10-6时,认为当前时间步内的数值计算已经收敛。
3 模拟结果分析
在同等计算资源配置与网格离散方案状态下,不同的湍流模型在本文的计算过程中体现了不同的耗时表现。RNGk-ε湍流模型计算效率最高,其次是Standardk-ω湍流模型,再次是Standardk-ε湍流模型,Realizablek-ε与SSTk-ω湍流模型的计算效率最低,最高效率与最低效率约相差1.5倍机时。
为保证各个湍流模型的计算结果具有可对比性,开始记录数据时要求各个湍流模型的计算结果均已进入统计定常阶段且至少达到20个以上涡脱周期。本文记录了20 000个时间步长的流场参数,对应的物理时间为10 s,获得的方柱旋涡脱落在100个周期以上。
3.1 整体气动力特性
非定常计算得到的流场变量都表现出脉动特性,气动力参数需要采用统计方法获得。本文采用Lyn的水洞试验结果(Re=21 400)[18-19],Franke的三维RANS模拟结果(Re=22 000)[20]以及Grigoriadis的三维大涡模拟结果(Re=22 000)[21]作为整体气动力的参考值。
各湍流模型在不同离散方案下计算的Strouhal数如图4所示。Realizablek-ε湍流模型的计算结果偏大,但受网格变化的影响较小,与试验值的相对误差最小为4.6%,最大为5.3%;SSTk-ω湍流模型的计算结果受网格数量变化的影响最大,与试验值的相对误差最小为5.3%,最大为15.9%;Standardk-ω湍流模型的计算结果与Franke的三维模拟结果吻合较好,与试验值的相对误差最小为0.8%,最大为2.3%;RNGk-ε湍流模型的计算结果与Standardk-ω湍流模型较接近,与试验值的相对误差最小为0.8%,最大为4.5%;Standardk-ε湍流模型的计算结果与试验值相差最大,相对误差最大为15.9%,最小为13.6%。
Strouhal数作为表征涡脱频率的参数之一,从图4可以看出Standardk-ε湍流模型模拟的涡脱频率最小,Realizablek-ε湍流模型计算的涡脱频率普遍较大;对于二维RANS模拟,Standardk-ω湍流模型对方柱绕流涡脱的捕捉能力明显优于其余湍流模型。

图4 不同工况下的Strouhal对比图Fig.4 Compariosn of Strouhal under various cases
阻力系数是方柱绕流数值模拟的难点之一。图5显示了各个湍流模型统计的阻力系数平均值随网格数增加而变化的趋势。SSTk-ω湍流模型的统计结果与试验值的相对误差最小为0.9%,最大为14.8%;RNGk-ε湍流模型的统计结果受网格变化的影响程度与SSTk-ω湍流模型相似,与试验值的相对误差最小为2.7%,最大为14.3%;Realizablek-ε湍流模型的统计结果分布于试验值与大涡模拟值之间;Standardk-ω湍流模型的统计结果与试验值的吻合程度优于其余湍流模型,其与试验值的相对误差最小为1.8%,最大为3.4%;Standardk-ε湍流模型的计算结果最小。
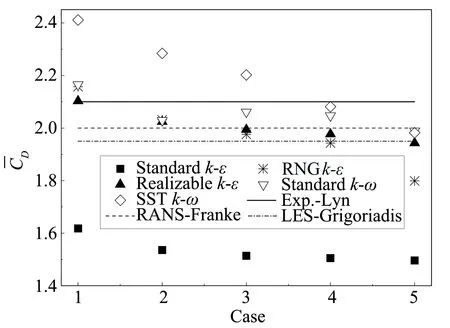
图5 不同工况下的阻力系数平均值对比图Fig.5 Comparison of under various cases
回流区长度Lr是数值模拟的另一难点。对比图6所示各个湍流模型统计的回流区长度可知,除Standardk-ε湍流模型外,其余湍流模型的计算结果普遍低于Lyn的试验值,在RNGk-ε与Realizablek-ε湍流模型算得最小试验相对误差为7.9%以及SSTk-ω湍流模型算得最大试验相对误差为21%之间随网格数变化而上下浮动;Standardk-ε与RNGk-ε湍流模型统计的回流区长度受网格变化的影响程度大致相似。
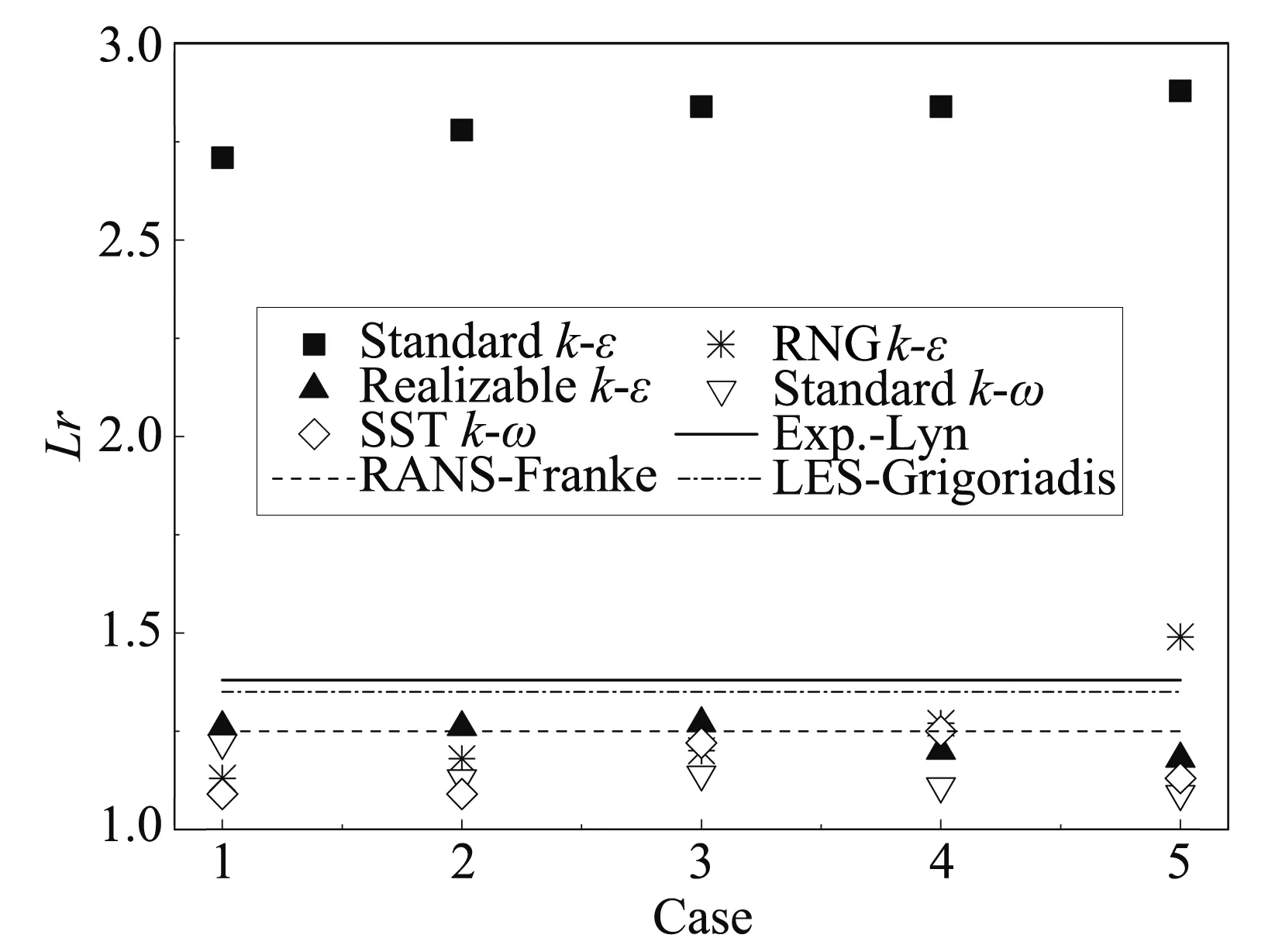
图6 不同工况下的回流区长度对比图Fig.6 Comparison of Lr under various cases
升力系数脉动均方根分布如图7所示。Standardk-ε湍流模型的计算结果受网格变化的影响最小;Standardk-ω与Realizablek-ε湍流模型湍流模型的统计结果随网格数量增加的变化趋势基本相同;RNGk-ε湍流模型的统计结果随网格数增加而降低;SSTk-ω湍流模型的计算结果整体大于其余湍流模型的计算结果。
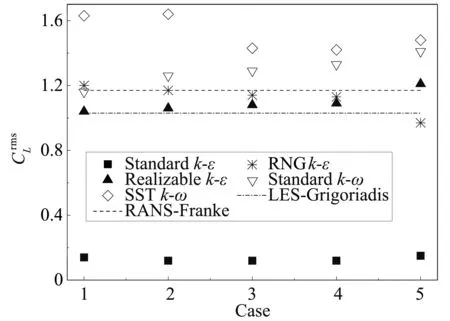
图7 不同工况下的升力系数脉动均方根对比图Fig.7 Comparison of under various cases
阻力系数脉动均方根分布如图8所示。SSTk-ω湍流模型的计算结果整体大于其余湍流模型的计算结果且受网格变化的影响最明显;其余湍流模型计算的阻力系数脉动均方根小于Grigoriadis的大涡模拟结果,Standardk-ε湍流模型的计算结果最小。
从上述对比分析可知:湍流涡粘模型的各项计算结果随网格数量增加呈现出不同的变化规律。一种湍流模型采用不同网格离散方案导致不同的计算结果;不同的湍流模型采用同一种网格离散方案也导致不同的计算结果。对于Strouhal数,离散方案三计算的结果优于其余方案;对于阻力系数平均值,离散方案三与方案四的结果比较好;对于回流区长度,各个方案的计算结果大致相当;对于升力系数脉动均方根,离散方案三与方案四的结果优于其余方案;对于阻力系数脉动均方根,离散方案三的结果最优。后续分析采用离散方案三的计算结果,表2展示了采用离散方案三时各个湍流模型计算得到的Y+极值。

图8 不同工况下的阻力系数脉动均方根对比图Fig.8 Comparison of under various cases
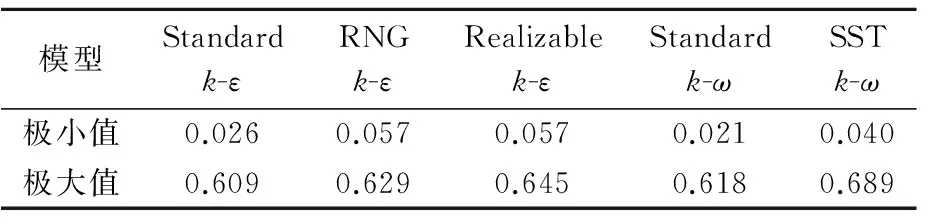
模型Standardk-εRNGk-εRealizablek-εStandardk-ωSSTk-ω极小值0.0260.0570.0570.0210.040极大值0.6090.6290.6450.6180.689
3.2 方柱表面压力分布
方柱所受的气动阻力大小与方柱表面的压力分布有直接联系。定义平均压力系数的表达式为:

(20)
其中p为监测点压力,p0为参考压力,本文参考压力为零。监测点压力系数平均值在方柱表面的分布如图9所示。Chen的试验研究[22]对应的来流风湍流度小于0.5%,Re=16 000,与本文Re=22 000接近。图中各条曲线表明:方柱的来流迎风面(179~191号测点)为正压区,各个湍流模型的计算得到的压力系数平均值与试验值吻合良好;在方柱的背风面(203~215号测点)及上下两侧面(192~203号测点,216~226号测点)为负压区,因为在方柱边角位置发生了流动分离,导致分离层内的压力显著降低。除Standardk-ε湍流模型获得的负压力系数平均值明显较大以外,RNGk-ε、Realizablek-ε以及Standardk-ω湍流模型三者的计算结果较接近且与试验值具有相同的走势,SSTk-ω湍流模型计算得到的统计值最小。这与图5描述的平均阻力系数分布相吻合,表明Standardk-ε湍流模型预测流动分离存在明显的劣势。方柱绕流阻力主要来自于迎风面与背风面的压力差,Standardk-ε与SSTk-ω湍流模型分别具有最小与最大的压力差,代表最大的阻力结果与最小的阻力结果。
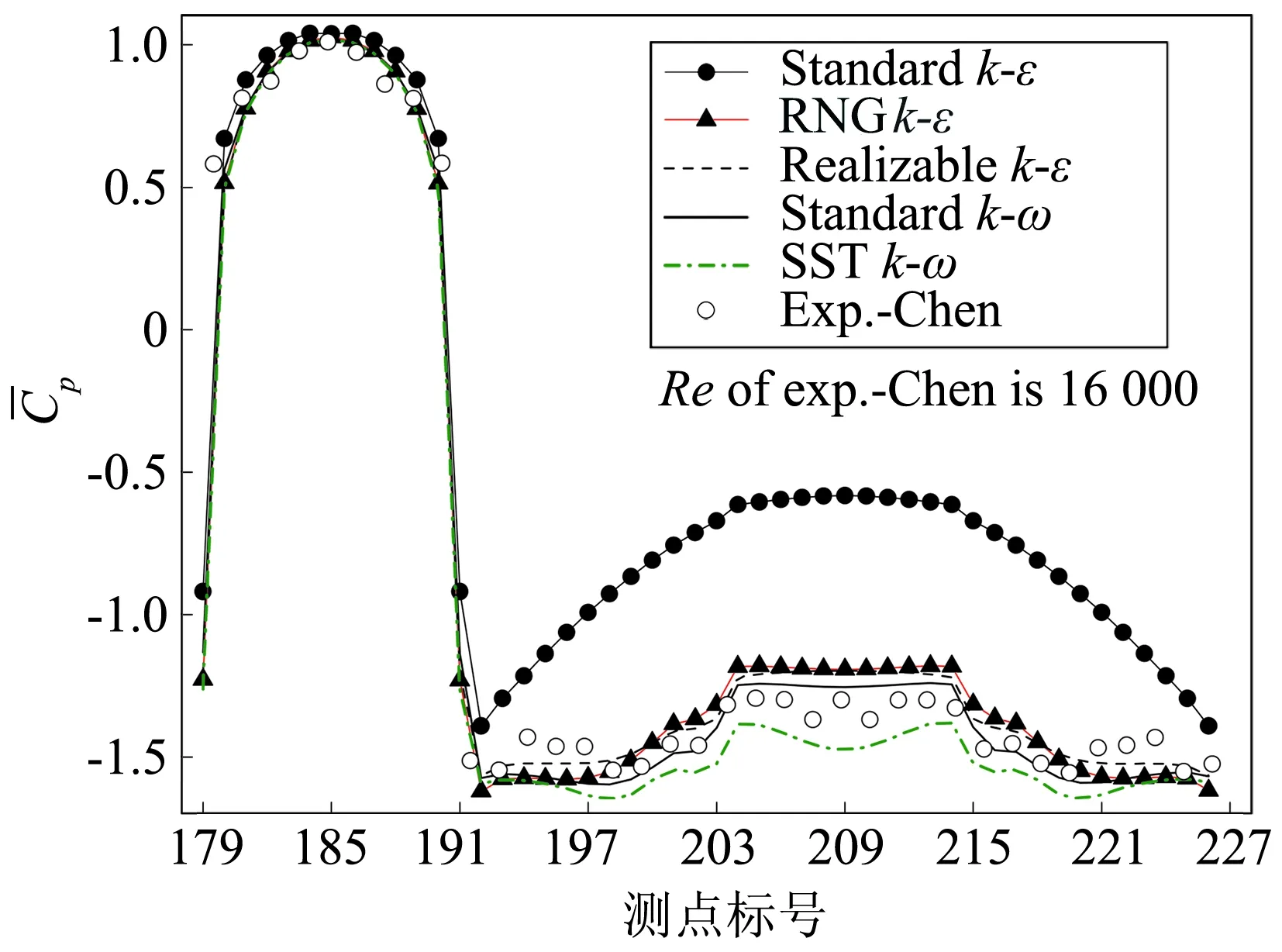
图9 方柱表面压力系数平均值 around the square cylinder
方柱表面的脉动压力主要受涡旋运动的影响,涡旋运动越剧烈,脉动越明显。因为输运方程的差异,不同湍流模型计算得到不同程度的涡旋运动。图10描述了方柱表面压力非定常特性的压力系数脉动均方根值,反映出流场漩涡做非定常运动的强弱。在迎风面中点位置处(185号测点)和背风面中点处(209号测点)分别出现压力系数脉动均方根极小值,表明此处压强受涡脱的影响最小;角点179与角点191附近的压力系数脉动均方根出现剧烈变化,表明此两处压强受涡脱的影响最大,即涡脱发生位置。图中各曲线的排列表明:Standardk-ε湍流模型计算的涡旋运动最弱,SSTk-ω湍流模型计算的涡旋运动最强。

图10 方柱表面压力系数均方根 around the square cylindert
涡脱是控制流场变化的主要因素之一。通过对各个湍流模型监测的测点脉动压力时程作功率谱密度(PSD)分析发现:除SSTk-ω湍流模型外,方柱各测点脉动压力的卓越频率与各自对应的湍流模型计算得到的涡脱频率相等,没有出现低于主涡脱频率的运动。这不符合Norberg[23]关于涡脱应该集中在一个频带上的观点,说明两方程雷诺平均涡粘模型进行二维模拟具有局限性,不能准确反映湍流的三维基本流动特征。
3.3 尾流中心线上的湍动能与速度
定义统计意义下的无量纲湍动能K=k/U2,本文算得的尾流区中心线上的湍动能如图11所示。从各湍流模型的计算结果与Lyn的试验结果和Bouris的大涡模拟结果(Re=22 000)[24]对比图可以看出:本文计算结果的峰值相对参考值要小。因为湍流本质上是三维的,二维计算使得尾流区湍流模拟不充分是导致本文计算的湍动能小于参考值的原因之一。SSTk-ω湍流模型计算的湍动能值高于其余湍流模型,但其峰值仍比试验结果要小29%,比LES模拟结果要小20%,但三者的下降速率大体一致;RNGk-ε与Realizablek-ε、Standardk-ω这三个湍流模型的峰值基本相同,但下降速度慢于SSTk-ω湍流模型。
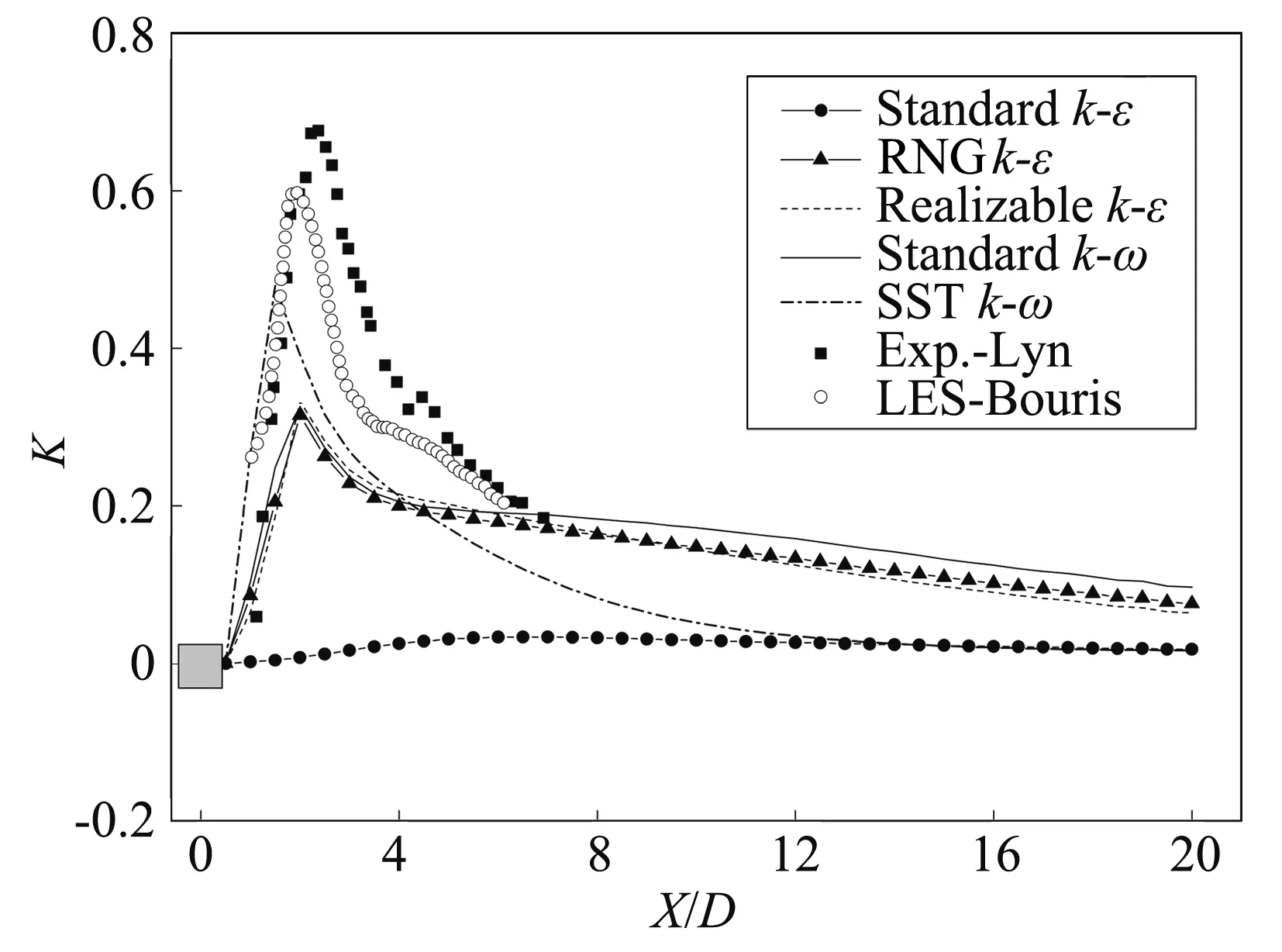
图11 尾流中心线湍动能分布Fig.11 Turbulence kinetic energy along thecenter line in the wake
方柱尾流区中心线上的平均流向速度Uavg分布如图12所示。SSTk-ω湍流模型与Lyn的试验结果吻合良好;RNGk-ε湍流模型、Realizablek-ε湍流模型以及Standardk-ω湍流模型的计算结果相互接近且与Grigoriadis的大涡模拟结果吻合较好;Standardk-ε湍流模型的远场流域结果靠近RNGk-ε湍流模型。
除Standardk-ε湍流模型外,在X<2的范围内,所有算例的恢复速度明显上升;在X>2后,SSTk-ω湍流模型的计算结果增长速度变慢,增长至0.58U后基本保持平稳;其余湍流模型约在X>6后计算结果保持平稳,远场速度恢复至0.8U附近。
尾流区中心线上速度的脉动情况是表征湍流特性的重要参数。图13与图14分别表示方柱尾流区中心线上的流向速度脉动均方根urms与横向速度脉动均方根vrms的分布。SSTk-ω湍流模型的计算结果虽然与参考值存在一定的偏差,但与试验值的变化趋势一致;而对于横向速度的脉动均方根,除Standardk-ε湍流模型外,其余湍流模型在达到峰值前均与参考值吻合良好,约在X=2D位置处达到峰值;之后SSTk-ω湍流模型与参考值的吻合程度明显优于其余湍流模型。
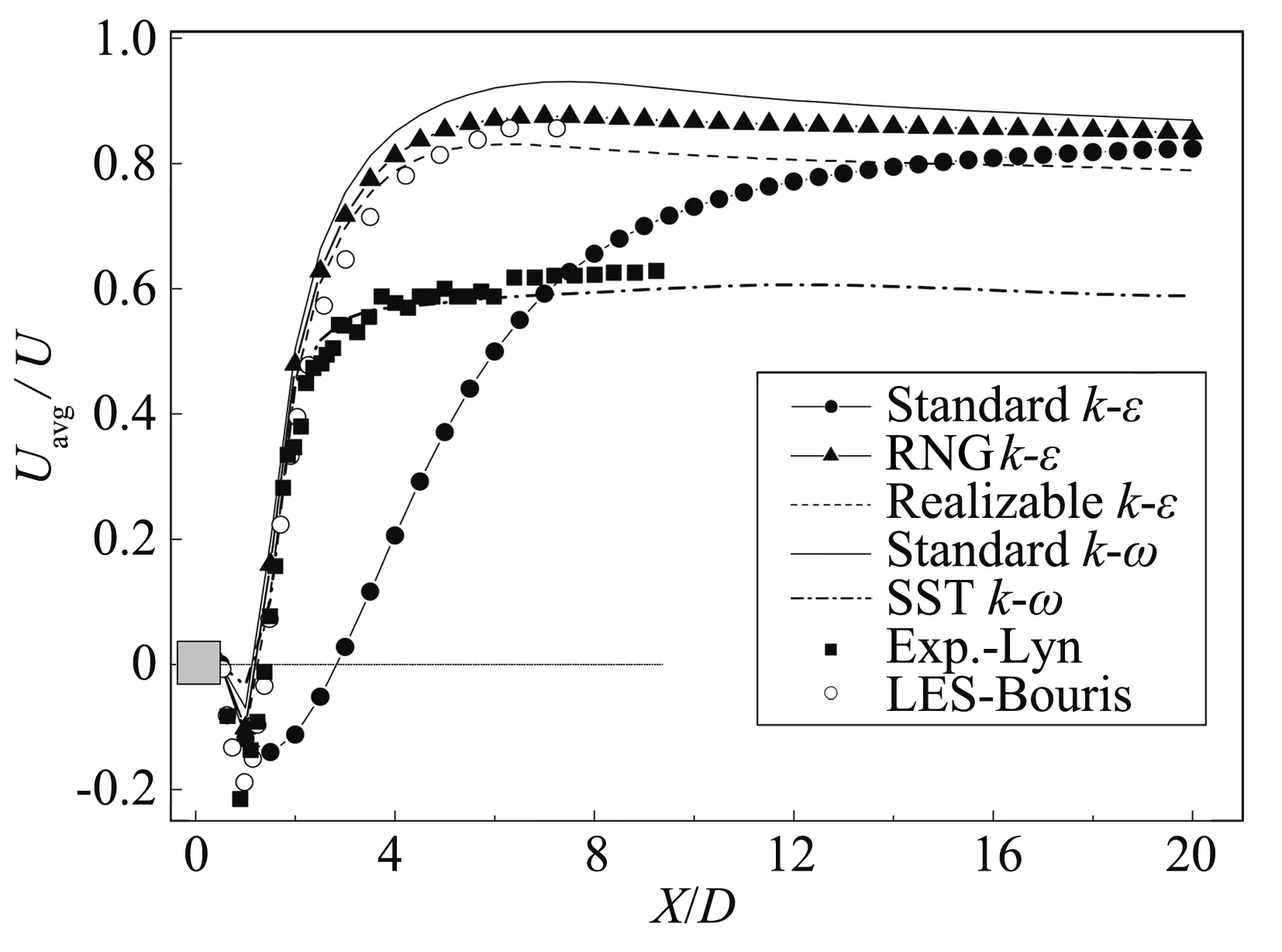
图12 尾流中心线流向速度平均值Fig.12 Uavg along the center line in the wake

图13 尾流中心线流向速度脉动均方根Fig.13 urms along the center line in the wake

图14 尾流中心线横向速度脉动均方根Fig.14 vrms along the center line in the wake
对比图13与图14可知:本文计算的横向速度脉动均方根峰值远大于流向速度脉动均方根峰值,表明方柱尾流涡的横向运动比流向运动更剧烈。
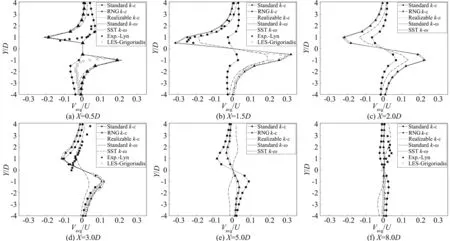
3.4 尾流区的平均速度剖面
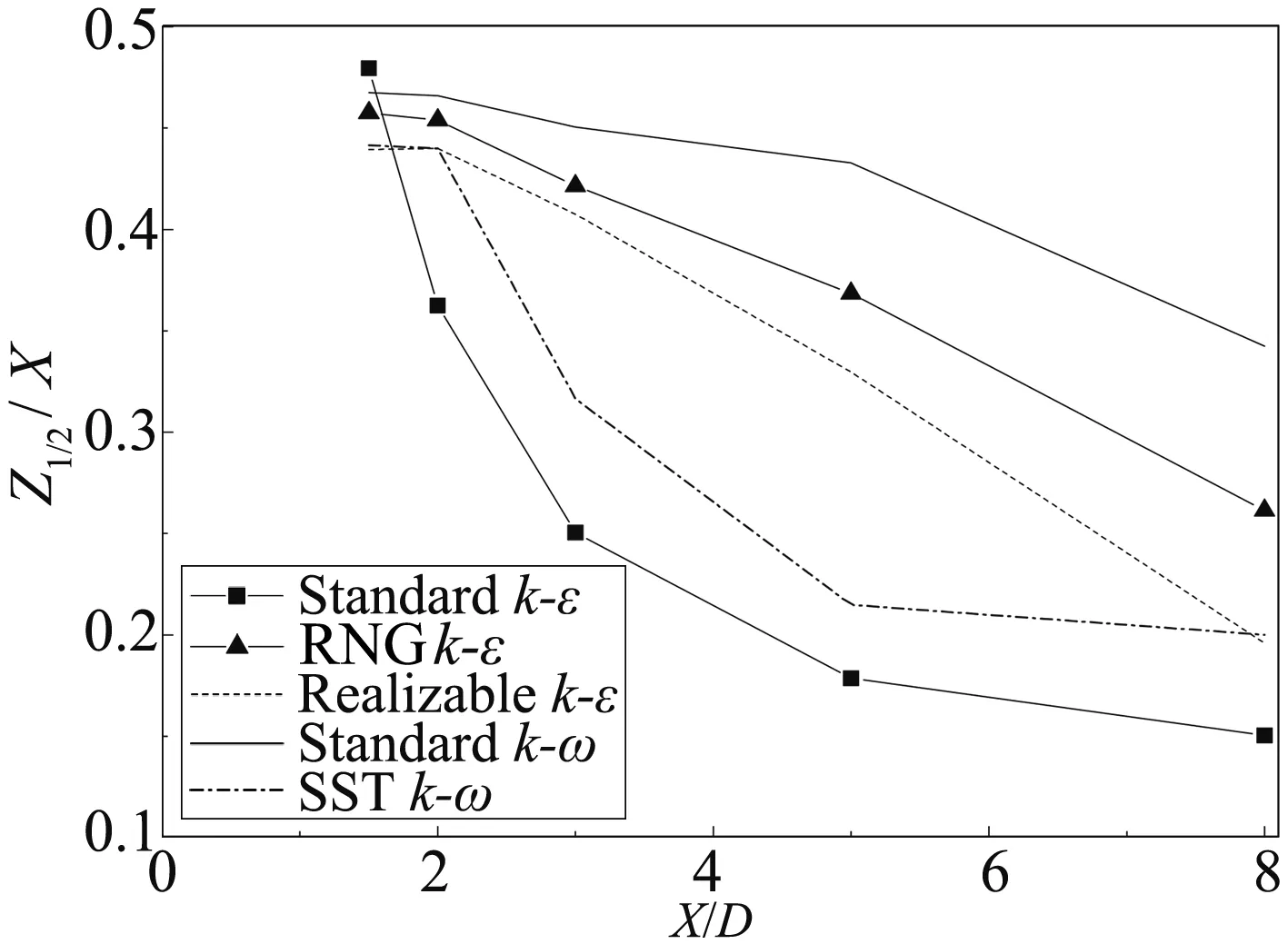
本文模拟得到的尾流区流向平均速度剖面如图15所示。因为方柱前沿存在流动分离现象,涡旋运动的动量亏损导致尾流区内的速度降低。流体随着剖面位置向下游移动,相同湍流模型在同一剖面上不同位置处的速度差显著减小,且与参考值的吻合程度明显降低。不同剖面上的速度分布曲线变化体现了尾流区主剪切层的钝化规律,各个湍流模型统计结果的差异也主要体现在这一区域内。从图15可以看出流向速度剖面沿中心线呈对称分布,本文模拟的主剪切层厚度约在中心线附近-1.5 在X=0.5D剖面,各个湍流模型的模拟结果在主剪切层内与参考值吻合良好,在剪切层边缘处的模拟结果均小于参考值;RNGk-ε与Realizablek-ε湍流模型的流向速度梯度最大,SSTk-ω湍流模型最小;在X=1.5D剖面,Standardk-ε湍流模型在主剪切层内的流向速度梯度最大,其在主剪切层外缘的模拟速度与大涡模拟结果吻合良好,其余湍流模型在主剪切层内的速度与大涡模拟结果吻合较好,RNGk-ε、Realizablek-ε与Standardk-ω湍流模型的流向速度梯度基本一致,SSTk-ω湍流模型的流向速度梯度依然最小;当尾流扩展至X=3.0剖面位置,SSTk-ω湍流模型的模拟结果全剖面与试验结果吻合良好,Standardk-ε湍流模型在主剪切层内的流向速度梯度依然最大,其次是SSTk-ω湍流模型;在X=5.0D剖面,主剪切层厚度略微扩大,Standardk-ε湍流模型在主剪切层内缩小了与其余湍流模型的流向速度梯度差异,SSTk-ω湍流模型扩大了与RNGk-ε、Realizablek-ε以及Standardk-ω湍流模型在主剪切层内的流向速度梯度的差异;在X=8.0D剖面,主剪切层厚度已经不明显,SSTk-ω湍流模型在全剖面的速度梯度最大,Standardk-ω湍流模型则进一步缩小了与其余湍流模型在速度梯度上差异。 各个湍流模型在尾流区不同剖面处的横向平均速度分布如图15所示。所有湍流模型的计算结果均表明:横向速度在中心线附近-1.0 综合对比分析图16可知:各个湍流模型计算结果之间的差异随着剖面位置向下游移动而明显减小,而且同一剖面上不同位置处的横向速度差也随剖面位置向下游移动而明显降低;Standardk-ε湍流模型的计算结果沿流场变化最小,SSTk-ω湍流模型的计算结果沿流场变化最大,RNGk-ε、Realizablek-ε以及Standardk-ω湍流模型的计算结果始终相互接近。图中各曲线显示本文的模拟结果更接近大涡模拟结果。 图15 尾流区不同截面处流向速度平均值Fig.15 Comparison of Uavg in the wake 图16 尾流区不同截面处横向速度平均值Fig.16 Comparison of Vavg in the wake 方柱尾流区的流动为自由剪切流。尾流特征半厚度作为一种表征尾流区特征长度的物理量,可以反映出尾流区自由剪切流的扩散率。定义尾流区半厚度为Z1/2,在该厚度边缘处的流向速度为: (21) 式中,u0(x)为尾流区中心线上的流向平均速度。本文计算的各个湍流模型的尾流特征半厚度沿程分布如图17所示。 图17 尾流特征半厚度流程变化Fig.17 Half self-similar profile of the wake 1) 网格数量变化对具体湍流模型各项计算结果精度的影响不尽相同。在确定的计算域内,网格划分数量并非越密集越好,本文的结果表明:二维模型网格数量约为Re数的3倍时, RANS模拟可取得较优的结果。 2) 在涡脱频率方面(Strouhal数),SSTk-ω湍流模型的计算值受网格数量的影响十分明显;其它几类模型均对网格数量不敏感。与试验值相比, Standardk-ε模型几类网格方案的计算值明显偏小,差值在13%左右。 3) 在平均阻力系数方面,SSTk-ω湍流模型与RNGk-ε模型的计算结果受网格数量影响显著,且随着网格加密,阻力系数单调减小,这两类模型明显存在一个最优网格划分方案;其它几类模型均对网格数量不敏感。但同样的,与涡脱频率类似,Standardk-ε模型的阻力系数计算值明显低于试验值,相差达28%左右,劣于其它模型。 4) 在方柱表面压力分布方面,各类模型在迎风面上的平均风压基本一致,明显的差异体现在侧风与背风面的负压区。Standardk-ε模型负压绝对值十分显著地低于其它模型,合理解释了该模型阻力系数偏低的原因。此外,在脉动风压方面, SSTk-ω湍流模型模拟的脉动量最高,RNGk-ε、Realizablek-ε的模拟结果大致相当,Standardk-ε湍流模型的压力脉动量最低。 5) 在尾流区中心线上,SSTk-ω湍流模型模拟的流向速度平均值与横向速度脉动均方根与试验数据吻合良好,优于其它RANS模型;RNGk-ε、Realizablek-ε以及Standardk-ω湍流模型的计算结果大致相当;对于湍动能分布,二维RANS湍流模型的计算结果明显低于试验值。 (6) 随着无量纲距离X/D的增加,各模型模拟得到的尾流区剪切层厚度相差明显。Standardk-ω模型的剪切层厚度最大。Standardk-ε模型的剪切层厚度最小,最小的尾迹宽度再次表明了其明显偏小的阻力系数。 参考文献: [1]Miranda S D, Patruno L, Ricci M, et al.Numerical study of a twin box bridge deck with increasing gap ration by using RANS and LES approaches[J].Engineering Structrues, 2015, 99: 546-558. [2]Zhu Zhiwen.Feasibility investigation on prediction of vortex shedding of flat box girders based on 2D RANS models[J].Chinese Journal of Highway and Transport, 2015, 28(6): 24-33.(in Chinese)祝志文.基于二维RANS模型计算扁平箱梁漩涡脱落的可行性分析[J].中国公路学报, 2015, 28(6): 24-33. [3]Giuseppe V.A numerical model for wind loads simulation on long-span bridges[J].Simulation Modelling Practice and Theory, 2003, 11: 315-351. [4]Lin Huang, Haili Liao, Bin Wang, et al.Numerical simulation for aerodynamic derivatives of bridge deck[J].Simulation Modelling Practice and Theory, 2009, 17: 719-729. [5]Tominaga Y, Mochida A, Yoshie R, et al.AIJ guiderlindes for practical applications of CFD to pedestrian wind environment around buildings[J].Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 1749-1761. [6]Sohankar A.Large eddy simulation of flow past rectangular-section cylinders: Side ratio effects[J].Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 640-655. [7]Yu D H, Butler K, Kareem A, et al.Simulation of the influence of aspect rations on the aerodynamics of rectangular prisms[J].Journal of Engineering Mechanics, 2013, 139(4): 429-438. [8]Bruno L, Salvetti M V, Ricciardelli F.Benchmark on the aerodynamics of a rectangular 5∶1 cylinder: An overview after the first four years of activiey[J].Journal of Wind Engineering and Industrial Aerodynamic, 2014, 126: 87-106. [9]Markatos N C.The mathematical modelling of turbulent flows[J].Applied Mathematical Modelling, 1986, 10(3): 190-220. [10]Launder B E, Spalding D B.Lectures in mathematical models of turbulence[M].London: Academic Press, 1972. [11]Yakhot V, Orszag S A.Renormalization group analysis of turbulence.I.Basic theory[J].Journal of Scientific Computing, 1986, 1(1): 3-51. [12]Shih T H, Liou W W, Shabbir A, et al.A newk-εeddy viscosity model for high reynolds number turbulent flows[J].Computers & Fluids, 1995, 24(3): 227-238. [13]Wilcox D C.Turbulence modeling for CFD[M].California: DCW Industries, Inc., 1998. [14]Menter F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA, 1994, 32(8): 1598-1605. [15]Tamura T, Itoh Y, Wada A, et al.Numerical study of pressure fluctuations on a rectangular cylinder in aerodynamic oscillation[J].Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54: 239-250. [16]Tominaga Y, Mochida A, Yoshie R, et al.AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings[J].Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10): 1749-1761. [17]Kader B.Temperature and concentration profiles in fully turbulent boundary layers[J].International Journal of Heat Mass Transfer, 1981, 24(9): 1541-1544. [18]Lyn D A, Einav S, Rodi W, et al.A laser-doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J].Journal of Fluid Mechanics, 1995, 304: 285-319. [19]Lyn D A, Rodi W.The flapping shear layer formed by flow separation from the forward corner of a square cylinder[J].Journal of fluid Mechanics, 1994, 267: 353-376. [20]Franke R, Rodi W.Calculation of vortex shedding past a square cylinder with various turbulence models[M]//Turbulent Shear Flows 8.Springer Berlin Heidelberg, 1993: 189-204. [21]Grigoriadis D G E, Bartzis J G, Goulas A.LES of the flow past a rectangular cylinder using the immersed boundary concept[J].International Journal for Numerical Methods in Fluids, 2003, 41(6): 615-632. [22]Chen J M, Liu C H.Vortex shedding and surface pressures on a square cylinder at incidence to a uniform air stream[J].International Journal of Heat and Fluid Flow, 1999, 20(6): 592-597. [23]Norberg C.Interaction between freestream turbulence and vortex shedding for a single tube in cross-flow[J].Journal of Wind Engineering and Industrial Aerodynamics, 1986, 23: 501-514. [24]Bouris D, Bergeles G.2D LES of vortex shedding from a square cylinder[J].Journal of Wind Engineering and Industrial Aerodynamics, 1999, 80(1): 31-46.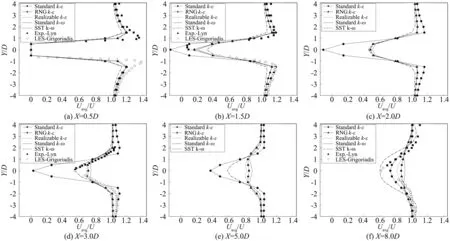
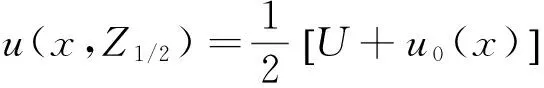
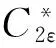
4 结 论
