MF-1模型飞行试验转捩结果初步分析

袁先旭, 何 琨, 陈坚强, 张毅锋, 王安龄, 国义军

(1.中国空气动力研究与发展中心 计算所空气动力研究所, 四川 绵阳 621000; 2.空气动力学国家重点实验室, 四川 绵阳 621000)

0 引 言

边界层转捩是经典物理学遗留的少数经典基础科学问题之一[1-2]，与湍流一道被称为“世纪难题”。对于高超声速飞行器来说，边界层转捩对TPS(热防护系统)的设计有十分重要的影响，设计时采用不同的边界层转捩准则，TPS的质量变化可达25%。目前，数值模拟与风洞试验仍不能全面、可靠地揭示边界层转捩机理，比如风洞试验无法模拟飞行时的来流扰动和壁温/总温比等参数，数值模拟采用的转捩预测模型需要标定系数。

众所周知，空气动力学研究有三大手段：风洞试验、数值计算、模型飞行试验(早期称模型自由飞)。我国著名科学家钱学森早在1960年代就指出“我们发展自己的飞机，要发展模型自由飞这种方法，解决风洞吹风不易解决的气动问题”。而高超声速边界层转捩就是一个典型的“风洞吹风不易解决的气动问题”，国际学术与工程界的普遍做法就是三大手段相结合，其中，模型飞行试验研究不可或缺[3-5]。如美国AFRL和澳大利亚DSTO联合实施的HIFiRE计划[6-8], 2006年11月启动，迄今未结束，共有3发研究边界层转捩问题(HIFiRE-1、5、9)。其中HIFiRE-1采用的试验模型为半锥角7°、前缘半径R2.5mm的圆锥(图1)，飞行试验虽只部分成功(RCS损坏)，但仍获得了4点独特结果：1) 得到了真实飞行环境下的转捩判据N值约为14，而地面风洞预测为4左右；2) 发现飞行上升段转捩过程呈现出一定的间歇性，初步推测其可能原因是转捩过程对飞行器姿态敏感；3) 发现返回段迎风子午线上，风洞转捩雷诺数高于飞行的新现象，初步推测其原因是在迎风子午线上由低壁温比产生的非稳定影响比由于风洞噪声产生的非稳定性影响大；4) 返回段，在圆锥肩部转捩之前出现了非预期的周期压力脉动，其两个主频(270 Hz和570 Hz)远低于第二模态和非定常横流涡模态，是否为定常横流涡模态，需要进一步研究。

目前，我国高超声速飞行器正在向“并跑”和“领跑”跨越，飞行器设计逐步摆脱国外参照物。此情况下，设计理念、设计思想对基础科学问题认知的依赖日益增长。比如多个先进飞行器的研制都对转捩机理、预测与控制提出了强烈需求。为此，中国空气动力研究与发展中心提出了首发验证性航天模型飞行试验任务(MF-1)，获取真实飞行条件下的气动数据，来验证地面风洞试验和数值计算预测的边界层转捩结果，进一步加深对相关气动机理的认识，提升高超声速气动热环境和气动力的预测精度，修正地面设计、计算和试验方法，进而指导高超声速飞行器设计。

2015年12月30日16点，MF-1模型飞行试验在中国酒泉卫星发射中心成功进行，全程飞行时间244.9 s，航程190.6 km，最大高度63.4 km，飞行最大马赫数5.3，获取了试验飞行器真实飞行环境下表面温度测量数据。试验取得圆满成功。试验后找到试验飞行器残骸和黑匣子，并且试验模型残骸完整。图2为试验飞行器残骸[9-10]。

图2 MF-1试验飞行器飞行试验残骸Fig.2 Flight test wreckage of MF-1

MF-1模型飞行试验是中国首次以空气动力学基础科学问题研究为目标的航天模型飞行试验，气动研究任务主要有以下几个方面：1)在真实的飞行环境中获取气动现象，得到边界层转捩(BLT)和激波边界层干扰现象(SWBLI)；2) 验证高超声速下的BLT和SWBLI现象的数值仿真方法及转捩预测模型；3)研究飞行试验、数值仿真、地面实验数据之间的相关性等等。本文就MF-1模型飞行试验在转捩测量方面的工作进行初步总结。

1 试验模型及测点布置方案

MF-1外形为轴对称的球头-锥-柱-裙构型，主要由测量锥舱(球锥、测量前锥舱、测量后锥舱)、测量直舱、仪器舱、连接段组成，如图3所示，以火箭发动机为助推系统，采用倾斜发射、无控飞行的方式。模型壳体材料为不锈钢，头部半径为R=5 mm，半锥角为7°，球锥长为1.1856 m，裙部半锥角为33°，模型总长为L=2.4626 m。

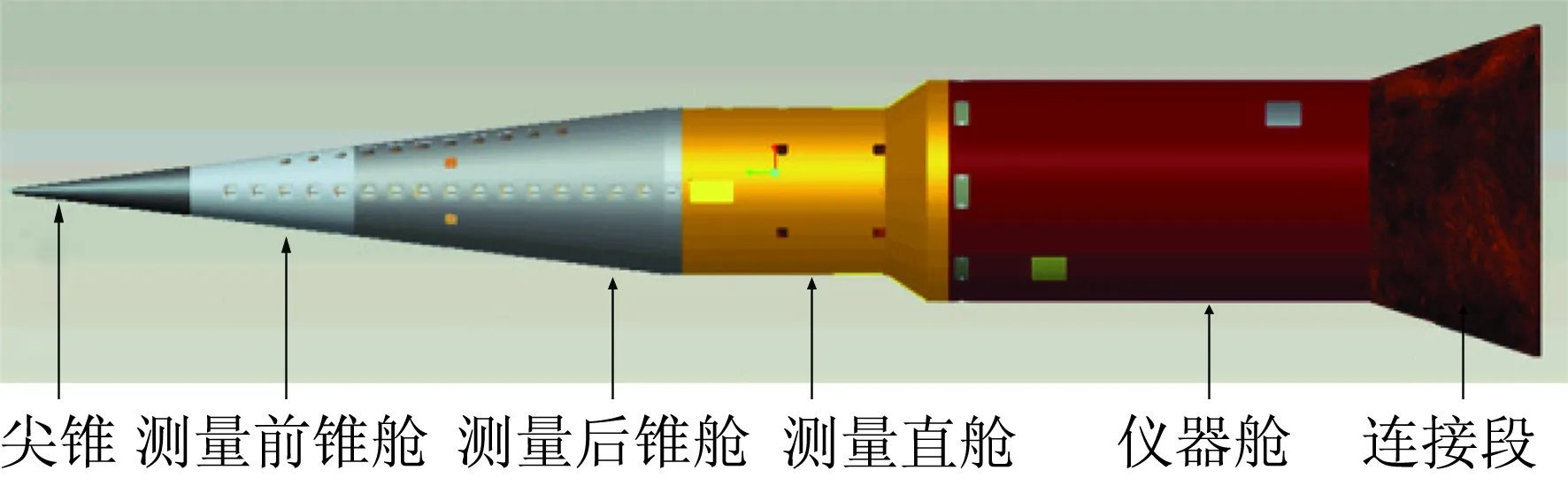
图3 试验模型组成Fig.3 Composition of test model

锥段温度测点40个(绿色)，在弹体表面沿流向开宽度20 mm的槽，再将该槽以2 mm厚的不锈钢扣板覆盖，温度测点布置在扣板内壁中心线上。采用非对称方式布点以测量转捩线沿周向分布情况。在周向一共布置四条沿流向的测温点，分别位于周向θ=0°、60°、120°、180°四个位置，起点位于X方向400 mm处，点与点之间沿X方向最小距离为50 mm。

图4 锥段测点布置示意图Fig.4 Cone transducer layout detail of MF-1

图5 锥段温度测点布置实物照片Fig.5 Physical map of cone temperature transducer layout

2 温度测量与热流辨识

MF-1通过测量的头锥表面温度分布辨识出热流分布进行转捩研究。

在测点分布区域，根据质心要求和结构设计需要，不同部位不锈钢壁面厚度有所不同，在锥段，前部厚度为22 mm，后部厚度为12 mm(见图6)。不锈钢的导热率比较低(约16 W/m·K)，直接测量金属内壁温度进行表面温度辨识，前后壁面温差很大，辨识的灵敏度较低。因此考虑减小测点位置的局部厚度，采用薄壁结构，减小前后壁面温差，提高热流辨识的灵敏度；这种厚度方面的差异会导致金属壁面温度的不同，从而产生明显的横向导热，使测得的后壁温度响应与一维加热情况明显不同。为减小薄壁的横向导热效应，将薄壁设计为变厚度结构，边缘部分厚度为2 mm，中间为较厚的圆形区域，在圆形中心位置安装热电偶测量温度，结构如图7。由示意图可以看到扣板四周与飞行器壁面结构通过焊接连接，而扣板下表面与壁面结构存在一个接触热阻环面(外方内圆)。图8为考虑不同接触热阻情况下的辨识结果。以后三维模型辨识采用接触热阻TCR=0.01的结果。

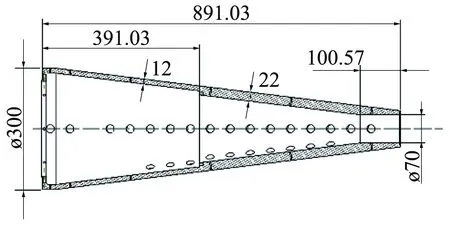
图6 锥体不锈钢壳体尺寸(mm)Fig.6 Stainless steel shell size of cone(unit: mm)

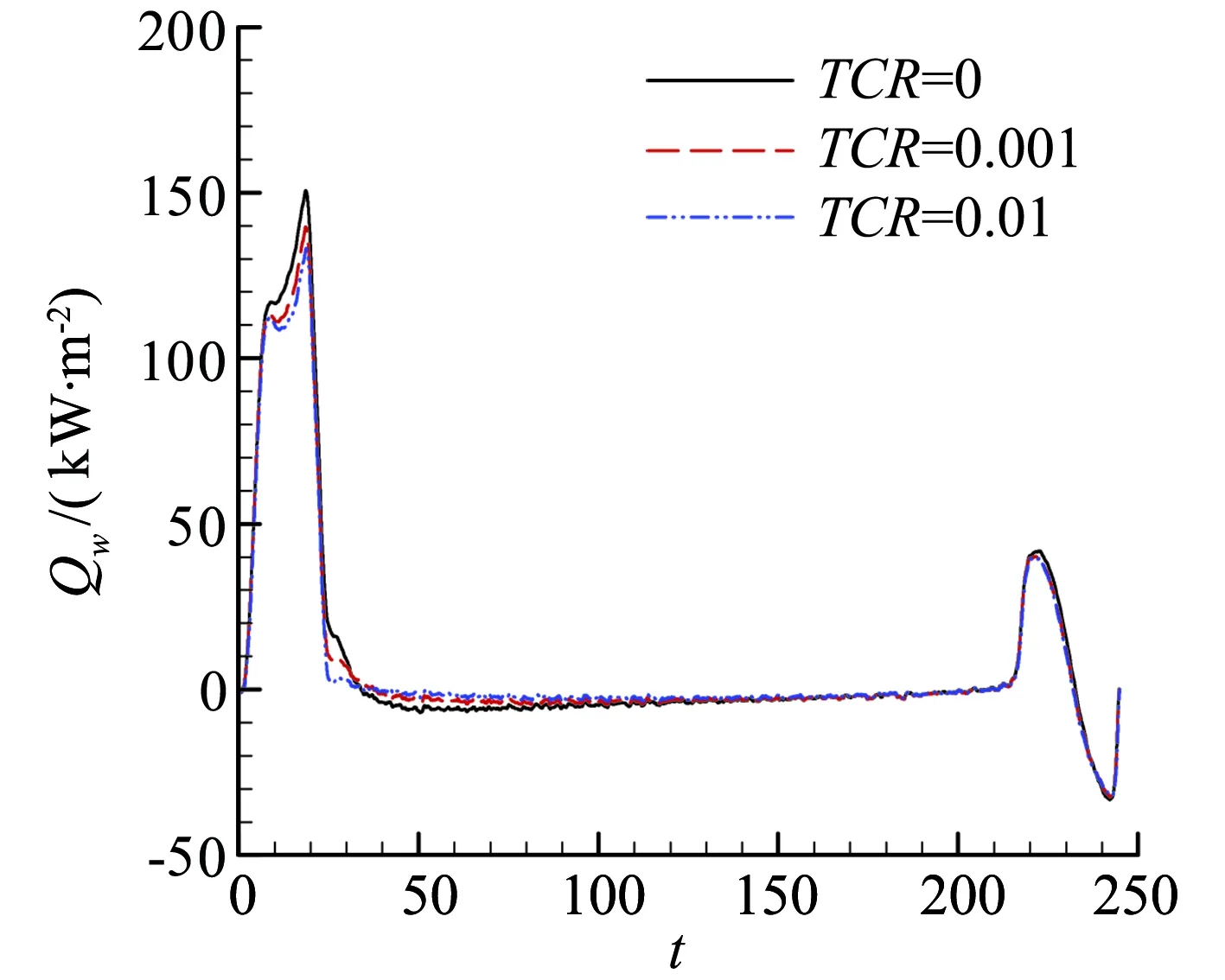
图8 不同接触热阻的热流辨识结果Fig.8 Heat flux identification results of differentthermal contact resistance

从测得的温度来辨识表面热流通常有一维模型、二维轴对称模型和三维模型三种方式。图9给出了三个不同模型得到的0°子午线上x=800 mm位置的表面热流随时间变化对比曲线。随着长时间的传热，测温结构和飞行器壳体之间的横向传热不可避免，由图9的辨识结果也可以看到由于没有考虑到横向传热20～60 s出现了明显的负热流。由二维和三维模型的辨识结果可以看到，二维和三维模型有效的改善了这一情况。由于二维模型没有考虑接触热阻，不加特别说明，本文以后的热流分析数据均采用三维模型辨识结果。

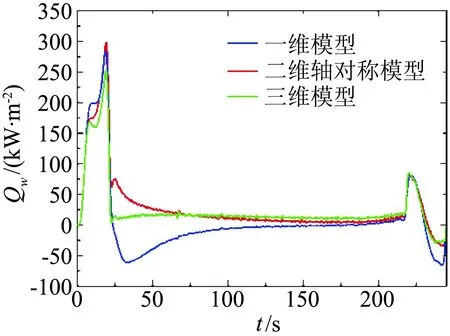
图9 不同辨识模型所得表面热流比较(x=800 mm)Fig.9 Compare of surface heat flux obtained by differentidentification model(x=800 mm)

3 MF-1飞行弹道

图10给出了最终辨识得到的MF-1飞行弹道与设计弹道的对比情况：在15.82 s试验飞行器高度为10.04km，进入上升段试验窗口，速度为1240.92 m/s，Ma数为4.14，总迎角0.19°，滚转角1062.45°,滚转角速度85°/s；19.52 s时飞行速度达到最大，为1571.61 m/s，Ma数为5.32，高度为13.92 km，总迎角0.41°，滚转角1400.86°,滚转角速度98°/s；在49.92 s试验飞行器高度为40.00 km，速度为1096.7 m/s，Ma数为3.46，总迎角1.97°，飞离上升段试验窗口，滚转角4138.28°,滚转角速度84°/s。在119.62 s达到弹道顶点，高度为63.35 km，速度为857.18 m/s，Ma数为2.77，总迎角3.77°，滚转角9873.64°,滚转角速度80°/s；在222.02 s此时处于再入段试验窗口，试验飞行器高度为14.3 km，速度为1060.19 m/s，Ma数为3.59，滚转角18 354.07°,滚转角速度97°/s。

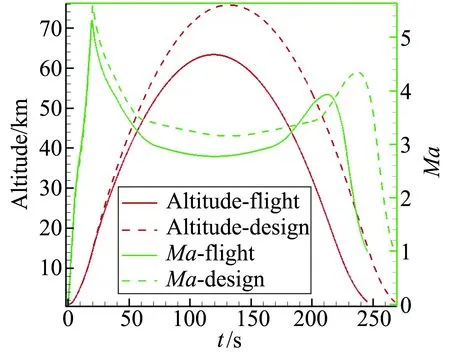
图10 飞行实测弹道与设计弹道对比Fig.10 Compare of as-flown and designflight trajectory of MF-1

图12给出了时刻10～30 s(上升段)和时刻210～230 s(下降段)的实际飞行雷诺数及马赫数随时间变化曲线。在上升段，随着高度增加，飞行雷诺数由于密度降低而急剧降低。而在下降段由于高度降低，密度增加，飞行雷诺数逐渐升高。

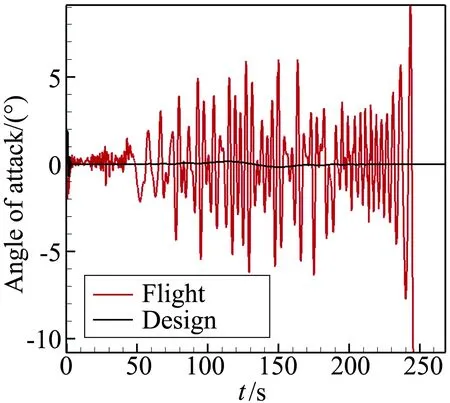
图11 飞行实测迎角与设计迎角对比Fig.11 Flight angle of attack of MF-1

图12 飞行雷诺数及马赫数随时间变化曲线Fig.12 Ascent and descent Reynolds andMach number flight histories

4 表面热流结果及转捩预测分析

图13和图14分别为上升段和下降段不同子午线上各个测点的热流随时间分布曲线。上升段时，在0°子午线上从x=450 mm到x=1150 mm各个测点位置流场再层流化(从湍流模态转变为层流模态)的发生时间基本相同(19 s)，而其余三个子午面上不同流向位置各个测点处流场再层流化时刻明显随时间变化，如60°子午线上，x=500 mm处在第13 s就发生了再层流化，x=650 mm处则在第18 s才发生。可以认为0°子午线上发生的强制转捩，其余子午线为自然转捩。

下降段时，60°、120°和180°子午线上沿流向各个测点处的转捩(从层流模态转变为湍流模态)时刻与上升段类似，位置靠后测点处流场先发生转捩，转捩位置随时间变化从后往前移动。在180°子午线上不大于500 mm位置的三个测点处一直没有转捩现象发生。而在0°子午线上，转捩发生的时间相对集中。

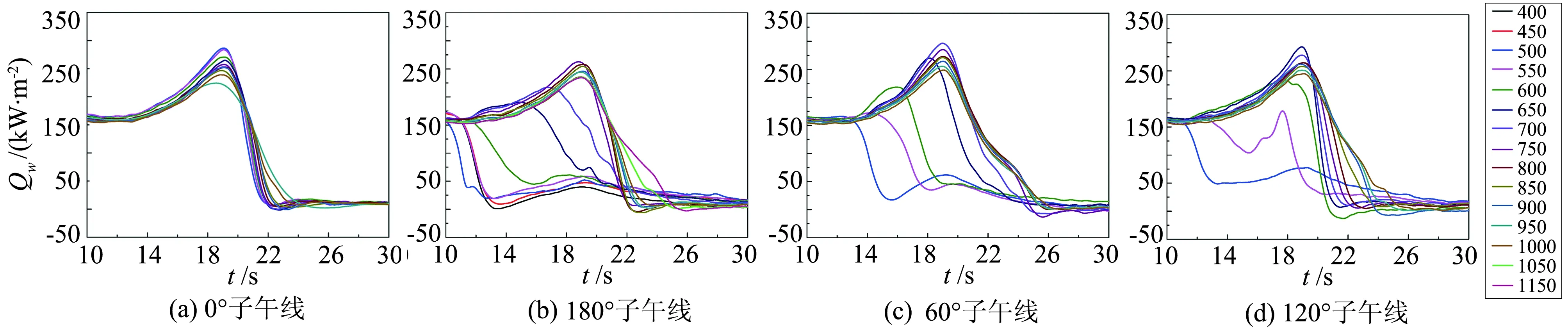
图13 10～30 s不同子午面热流随时间变化曲线Fig.13 Surface heat transfer histories at different meridian in 10～30 seconds

图14 210～230 s不同子午面热流随时间变化曲线Fig.14 Surface heat transfer histories at different meridian in 210～230 seconds

图16和图17给出了不同时刻不同子午线上测点辨识得到的热流沿流向分布曲线。从图中可以看出不同时刻不同子午线上再层流化或转捩位置。

180°子午线上热流分布曲线可得不同时刻该子午线上再层流化或转捩位置。上升段24 s后锥段转捩消失、下降段215 s后锥段出现转捩。

以下降段为例，215 s转捩发生时，转捩位置位于x=900 mm处，随高度降低，转捩位置前移，224 s时转捩位置移动到x=550 mm处。

0°子午线上下不同时刻转捩位置基本固定。如下降段，218 s时x=900 mm处发生转捩，但219 s时刻迅速前移到x=450 mm处并基本保持不动。

根据对模型外形的观察，初步推测为模型头部与身部相接部分因装配误差产生的台阶导致(h～0.2 mm)bypass转捩。

试验模型完成加工装配后，对尖锥-前锥舱和前锥舱-后锥舱对接处进行台阶高度测量，测量结果如图15所示(0°子午线位于第IV象限)，尖锥-前锥舱对接台阶最大值为0.2 mm，且为逆向台阶，台阶超差的原因为尖锥与前锥舱采用螺纹连接时出现同轴度偏差。

图15 锥段台阶测量值分布Fig.15 Step measurement value of cone

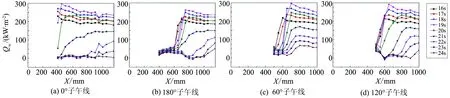
图16 上升段16～24 s不同时刻各子午线的热流分布曲线Fig.16 Surface heat transfer distributions in 16～24 seconds at different meridian

图17 下降段215～223 s不同时刻各子午线的热流分布曲线Fig.17 Surface heat transfer distributions in 215～223 seconds at different meridian

利用MF-1飞行试验数据对γ-Reθ转捩预测模型进行验证和标定，获得工程实用化的高超转捩预测模型。

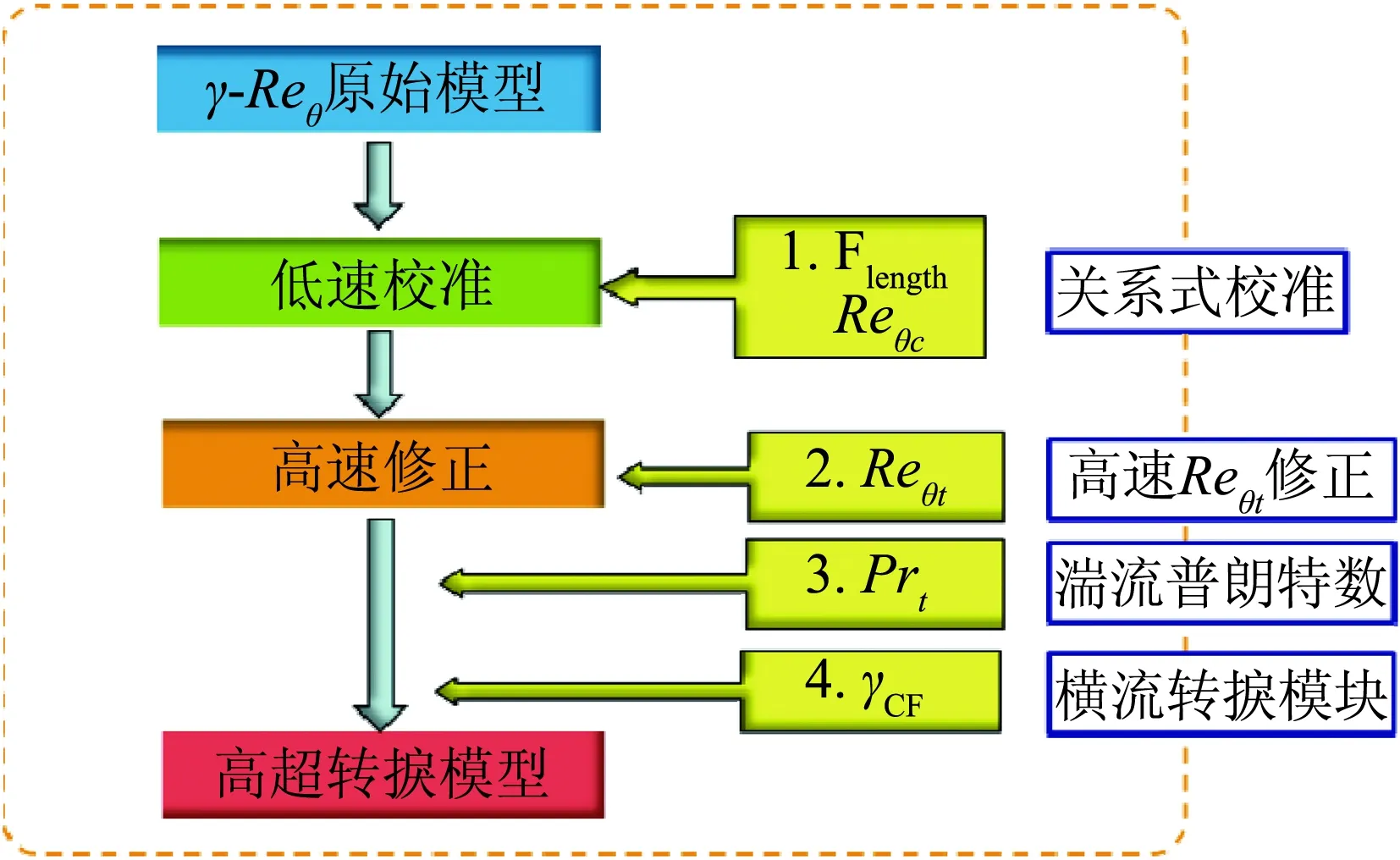
图18 转捩预测模型进行验证和标定方法Fig.18 Verification and calibration method oftransition predict model

对于光滑壁面，研究表明，影响边界层转捩的主要因素是局部Reynolds数和当地边界层外缘Mach数，工程上常用的光面转捩准则是：

1) “70-826”转捩准则。这是文献AIAA Paper 70-826[11]建议的转捩准则，后文称其为“70-826”转捩准则。开始转捩条件用下式确定：

(1)

其中，Me为当地边界层外缘马赫数，s为从驻点量起的物面弧长。

2) 动量厚度雷诺数转捩准则。Thyson等[12]首次采用动量厚度雷诺数判别转捩，与俄罗斯在联盟号飞船返回舱热环境预估[13-14]时采用如下转捩准则具有同一形式：

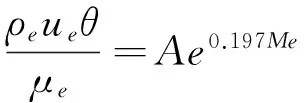
(2)

其中，θ为边界层动量厚度，系数A与来流条件和表面状况有关，范围在150～500内不等，对于光滑的不透气壁，文献[12]取A=200，文献[13]取A=300。

2) X-43飞行数据转捩准则。X-43准则[16]是基于飞行数据拟合得到的判断准则，故其与飞行数据吻合较好。

Reθ=305Me

(3)

利用飞行数据(辨识得到的飞行高度、姿态、速度等参数)对预测转捩模型进行验证，给出不同方法预测的转捩位置比较(见图19)。其中图中Eng1是利用工程中常用的70-826方法预测的转捩位置，Eng2是利用美国X-43飞行数据拟合的转捩判断准则预测的转捩位置。RANS是采用γ-Reθ转捩预测模型得到的结果。

从结果可以看出，70-826方法是采用风洞实验数据发展而来的转捩判断准则，故预测转捩与实际飞行数据相比较为靠前，是一种略微保守的转捩预测方法。X43方法是在飞行数据基础上发展起来的，故其与MF-1飞行实测数据吻合。

图19 不同方法预测的转捩位置比较Fig.19 Transition location of different predict method

利用经过MF-1飞行数据标定的γ-Reθ转捩预测模型对类似的HIFiRE-1飞行转捩情况进行了计算，得到如图20结果。

图20 HIFiRE-1转捩位置预测结果Fig.20 HIFiRE-1 Transition location predicted byChant software which calibrated by MF-1 flight data

从图20可以看出：利用MF-1飞行数据标定的转捩预测模型所预测的转捩位置和HIFiRE-1飞行结果符合较好。

图21给出了转捩位置随着时间或飞行高度的变化情况。可以看出，在上升段，模型随着火箭从地面升起，开始转捩的位置非常靠近头部，随着高度增加，转捩位置逐渐向后移动，直至离开锥体尾部。测点所在位置(x=400～1300 mm)在上升段先是处于湍流状态，随着高度增加逐渐过渡到层流状态。下降段情况刚好相反，模型下降过程中，转捩位置从尾部开始向前移动，测点所在位置先是处于层流状态，随着高度下降逐渐过渡到湍流状态。

测点位置在上升段由湍流完全变为层流TL和下降段由层流向湍流转捩LT其转捩准则是不同的，前者小于后者(图22)。比如采用俄罗斯的转捩准则，上升段系数A取300与实测曲线最为接近，但在下降段A取350或更大一些更靠近实测曲线，说明表面固定位置处的流动从湍流向层流过渡和从层流向湍流过渡存在转捩Re差异。

图21 转捩起始点沿弹道变化情况Fig.21 Histories of transition onset location

根据图21，上升段随着飞行高度增加，转捩起始点沿锥体表面向后移动，当转捩起始点经过测点所在位置时，该点流动状态由湍流完全变成层流，这时的转捩可以在比下降段较低的准则数下转捩。与此相反，下降段从层流向湍流转捩的滞后，表示需在较高的雷诺数下转捩。

5 结 论

通过对MF-1飞行试验转捩测量数据的初步分析表明：

1) 通过薄壁测温技术获取的真实飞行条件下的转捩数据是可靠的，为将给予RANS的转捩预测模型推广至高超声速提供了标定数据基础。

2) 发现了0.2 mm台阶/缝隙就可能诱导的边界层强制转捩现象，目前正在发展基于涡拉伸的涡粘性亚格子模型加以确认；相比于经典的Smagorinsky模型，VSV模型的涡粘性系数能够在层流区域退化为零，有利于模拟“层流-转捩-湍流”全过程。

3) 发现了上升段湍流-层流(再层流化)与下降段层流-湍流(转捩)的临界雷诺数差异，为工程转捩模型提供了标定数据。

MF-1作为我国首次针对高超声速空气动力学基础问题研究的航天模型飞行试验，其飞行试验成功进一步验证了飞行试验总体方案和测量技术的可行性，以及其对基础研究的无可替代的支撑作用，为我国航天模型飞行试验的长远发展奠定的基础。

参考文献：

[1]William S S, Helen L R, Edward B W.Stability and transition of three-dimensional boundary layers[J].Annu Rev Fluid Mech, 2003, 35: 413-40.

[2]Zhou H.Transiton prediction and turbulence computation of hypersonic boundary layers[J].Modern Defence Technology, 2014, 42(4): 1-8.(in Chinese)周恒.高超声速边界层转捩和湍流计算问题[J].现代防御技术, 2014, 42(4): 1-8.

[3]Adamczak D, Alesi H, Frost M.HIFiRE-1: Payload design, manufacture, ground test, and lessons learned.AIAA 2009-7294[R].Reston: AIAA, 2009.

[4]Alvaro M B, Martins S, Raffaele A, et al.EXPERT-The ESA experimental re-entry test-bed, trajectory and mission design.AIAA 2011-6342[R].Reston: AIAA, 2011.

[5] Eggers T, Longo J, Hörschgen-Eggers M, et al.The hyper-sonic flight experiment SHEFEX.AIAA 2005-3294[R].Reston:

AIAA, 2005.

[6]Kimmel R L.Aerothermal design for the HIFiRE-1 flight vehicle.AIAA 2008-4034[R].Reston: AIAA, 2008.

[7]Kimmel R L, Adamczak D, DSTO AVD Brisbane Team.HIFiRE-1 preliminary aerothermodynamic measurements.AIAA 2011-3413[R].Reston: AIAA, 2011.

[8]Adamczak D, Kimmel R L, Paull A, et al.HIFiRE-1 Flight Trajectory Estimation and Initial Experimental Results.AIAA 2011-2358[R].Reston: AIAA, 2011.

[9]Yang Q T, Zhou Y, Yuan X X, et al.Surface pressure and temperature measurement technology in MF-1 modelling flight test[J].Acta Aerodynamica Sinica, 2017, 35(5): 732-741.(in Chinese)杨庆涛, 周宇, 袁先旭, 等.MF-1模型飞行试验表面压力与温度测量技术研究[J].空气动力学学报, 2017, 35(5): 732-741.

[10]Ou C, Ji H L, Xiao H S, et al.Key problems in structure and thermal protection for MF-1 model testing flight vehicle[J].Acta Aerodynamica Sinica, 2017, 35(5): 742-749.(in Chinese)欧朝, 吉洪亮, 肖涵山, 等.MF-1模型飞行试验结构与热防护关键问题研究[J].空气动力学学报, 2017, 35(5): 742-749.

[11]Timmer H G, Arne C L, Jr Stokes T R, et al.Aerothermodynamic characteristics of slender ablating re-entry vehicles.AIAA-70-826[R].Reston: AIAA, 1970.

[12]Thyson N, Neuringer J, Pallone A, et al.Nose tip shape change predictions during atmospheric reentry[R].AIAA 70-827, 1970.

[13]赵梦熊, 等.“联盟”号返回舱空气动力专集[R].航天工业总公司第七一O所, 1995.

[14]Cline P B.Entry heat transfer[M]//SAE Aerospace Applied Thermodynamics Manual.Society of Automotive Engineers, Inc.2nd Ed, 1969: 517-598.

[15]Berry S A, Daryabeigi K, Wuster K.Boundary layer transition on X-43A.AIAA 2008-3736[R].Reston: AIAA, 2008.