知“错”就改 方能远行
——“相似三角形”解题错因分析与答题指导
2018-04-25李桂松
李桂松
“相似三角形”是初中数学的重要内容之一,也是解决数学问题的有效工具.由于这部分内容涉及知识点多、相似关系抽象、对应关系复杂、比例运算烦琐、综合性强等原因,许多同学在解题过程中错误频发.笔者现列举几种常见的典型错误予以剖析,希望对同学们有所帮助.
一、审题不严,造成取舍失误
例1 已知线段c是线段a、b的比例中项.若a=1,b=2,求c的值.
【错解】因为线段c是线段a、b的比例中项,所以c2=1×2=2,解得c=± 2.
【错因】这是由于审题不清、匆忙答题造成的.答题者忽略了题中的关键词“线段”,将线段与数字混为一谈,未能将不符合题意的负值舍去.
【答题指导】严谨审题是正确解题的前提条件.解题前同学们要仔细研读,找出题中的关键词,根据题意合理取舍,避免不必要的失误.因为线段c的值为正,所以c=2.
二、关系错乱,导致解题错误
例2 如图1,在四边形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e.则下列等式成立的是( ).
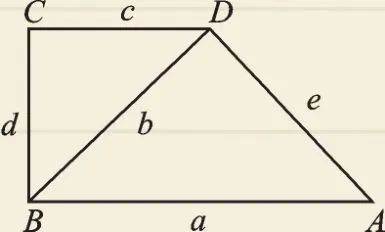
图1
A.b2=ce B.b2=ac
C.bc=de D.bd=ae
【错解】因为AB∥CD,所以∠CDB=∠DBA,又因为∠C=∠BDA=90°,所以△CBD∽△DBA,所以,易得bc=de,故选C.
【错因】本题是相似三角形的条件和性质的综合应用,解题的关键在于找准相似三角形的对应关系.上述错解中答题者未能找准两三角形对应的角和边,列出了错误的比例式,导致选错.
【答题指导】相似三角形对应边成比例,而全等三角形对应边相等,因此相似三角形的对应关系比全等三角形的对应关系更抽象,解题时容易出现对应关系错乱的现象.本题是根据“两角对应相等”来说明两个三角形相似的,所以通过对应角的顶点来确定对应关系不失为明智之举.由∠CDB=∠DBA得顶点D与B对应;由∠C=∠BDA=90°得顶点C与D对应;所以第三对对应点为剩下的点B与点A.这样易得△CDB∽△DBA,所以比例式的得出便不再困难.
三、判断失误,导致错用性质
例3 如图2,点D、E分别是△ABC边AB、AC的中点,BE、CD相交于点O.若△ABC的面积为6,则△COE的面积为______.

图2

【错因】答题者在△COE与△CDA不具备相似条件的情况下,使用了“相似三角形的面积比等于相似比的平方”.这属于无视定理使用条件,错误发生在所难免.
【答题指导】在解答相似三角形面积方面的问题时,同学们首先想到的是“相似三角形的面积比等于相似比的平方”.这是合理的思维,但一定要在具备相似条件的情况下运用.当不具备相似条件时,应转变思路寻求其他方法,“同高不同底,面积为底比”就是值得尝试的方法.如图3,连接DE,易得DE∥BC且,所以△DOE∽△COB,所以,根据三角形面积公式易得,即,由点E是AC的中点得6=3,所以S△COE=1.
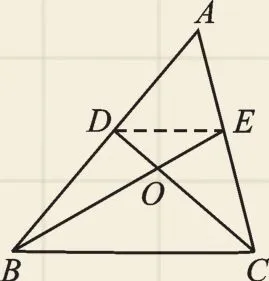
图3
四、理解不透,引起结果漏解
例4 如图4,在矩形ABCD中,AB=8cm,AD=6cm.点P以2cm/s的速度从点B出发向点A运动;同时,点Q以1cm/s的速度从点A出发向点D运动,当其中一个点到达终点,另一个点也停止运动.请问几秒时△APQ与△BCP相似?
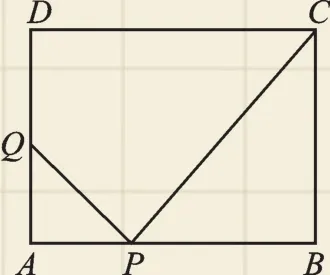
图4
【错解】设运动时间为t秒,则BP=2t,AP=8-2t,AQ=t.因为△APQ与△BCP相似,所以,解得,所以 时△APQ与△BCP相似.
【错因】由于答题者没有正确理解“相似”与“∽”的区别,将“△APQ与△BCP相似”的对应关系单一化处理,导致答案漏解.
【答题指导】正确理解“相似”与“∽”的区别是避免漏解的前提条件.“△APQ∽△BCP”有确定的对应关系,而“△APQ与△BCP相似”中的对应关系不确定,需要分类讨论.许多同学在解答类似问题时,思维容易受到题目中已有图形的影响,就图答题,出现漏解现象.因此,同学们解题时既要借助已有图形理清题意,又要超越已有图形,发散思维,穷尽所有可能.当△APQ∽△BCP时当△APQ∽△BPC时,有解得 t=-3± 33.又因为 0<t≤4,所以或( 33-3)s时,△APQ与△BCP相似.
错必有因,凡遇出错,我们不能总是以“粗心”为借口,只有找到错误的深层原因并加以纠正,才能避免同样的错误重复发生.知“错”善改,方得始终.愿同学们善待错误,在纠“错”中一路前行!
