问题成系列 做二要想一
2018-04-25李长春特级教师
李长春(特级教师)
不少中考解答题都由2~3个小题目组成,命题者常将一些有难度的题目分成几个小题目,以“台阶”式的设计将问题不断深入,第1问通常比较简单,容易入手,值得注意的是第1问往往也为第2、3两问的解答提供了一种思考的方向,我们解题时如果能根据命题老师所给的“路标”,拾级而上,踩点解答,往往能化难为易,达到事半功倍的效果.
例1 (2017·杭州)(本题满分8分)如图1,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
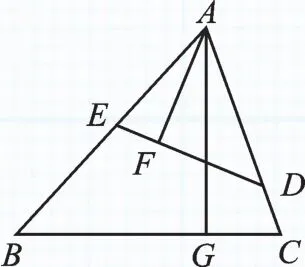
图1
(1)求证:△ADE∽△ABC;
【试题分析】在(1)中,结合条件在两个三角形中可找“两角分别相等”,事实上,它们已经有了一组公共角,再找出∠EAF和∠GAC的余角相等即可;在(2)中可以转化为哪两条边的比成为解题的关键,此时,结合(1)中的结论△ADE∽△ABC可得到∠ADF=∠B,再证得△ADF∽△ABG,将转化为即可.
【踩点解答】(1)证明:
∵AF⊥DE,AG⊥BC,
∴∠AFE=90°,∠AGC=90°,
∴∠AEF=90°-∠EAF,∠C=90°-∠GAC,
又∵∠EAF=∠GAC,
∴∠AEF=∠C,
又∵∠DAE=∠BAC,
∴△ADE∽△ABC(.踩点1:证两个角对应相等,4分)
(2)∵△ADE∽△ABC,
∴∠ADE=∠B,
又∵∠AFD=∠AGB=90°,
∴△AFD∽△AGB,(踩点2:证两个三角形相似,6分)
∵AD=3,AB=5,
【点评】解题时注意题目前后的连贯性,当第(2)问遇到困难时,一定要回头看第(1)问求证的结论,由这个结论还能得到什么?也许思路就在结论的延续中.
例2 (2017·武汉)(本题满分10分)已知四边形ABCD的一组对边AD,BC的延长线相交于点E.
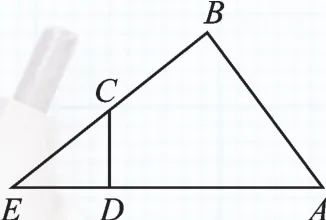
图2
(1)如图 2,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;
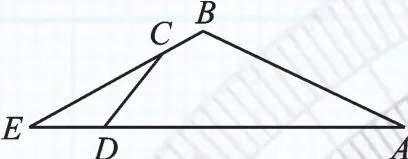
图3
(3)如图4,另一组对边AB,DC的延长线相交于点F,若cos∠ABC=cos∠CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).

图4
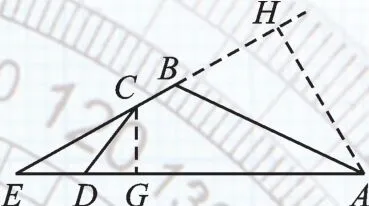
图5
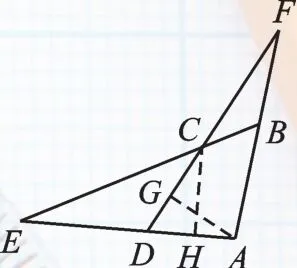
图6
【踩点解答】(1)证明:
∵∠ABC=∠ADC=90°,
∴∠ABE=∠CDE,
又∵∠E=∠E,
∴△EAB∽△ECD,(踩点1:证两个角对应相等,2分)
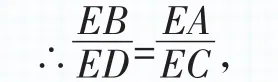
∴ED·EA=EC·EB.(踩点2:证得相似后得到结论,3分)
(2)如图5,过点C作CG⊥AD于点G,过点A作AH⊥BC交CB的延长线于点H.
∴DG=3,CG=4.
∵△CDE的面积为6,
∴ED=3,∴EG=6.
∵AB=12,∠ABC=120°,
∴BH=6,AH=63.
由(1)中方法得:△ECG∽△EAH,(踩点3:证得相似,求出相应线段,5分)
∴EB=EH-BH=93-6,
S四边形ABCD=S△ABE-S△CDE=75-18 3.
(踩点4:运用转化思想,将四边形面积转化为两个三角形面积之差,并算得结果,8分)
【点评】问题成系列,做二要想一,本题中的第(1)问暗藏模型,解第(2)问可以直接去找这样的模型并应用,第(3)问则对模型进行了适当的演变,但解题的思路还在(1)中,只要我们踩住这个点,问题就可迎刃而解.但需要注意的是,本题的前两问均以“若”开头,都是在假设的前提条件下进行设问的,所以做第(2)问时不能用第(1)问的结论,第(3)问也不能直接运用前两问的结论.正所谓:问题成系列,做二要想一;上题若如果,不能用结果.
