基于局部直方图信息的相似图像组分割模型
2018-04-24李欢丽徐海平王美清
李欢丽, 徐海平, 王美清
(福州大学数学与计算机科学学院, 福建 福州 350116)
0 引言
图像分割是图像处理和计算机视觉中最重要的任务之一[1]. 它的目的是将图像中感兴趣的对象与其余部分相分离, 以便为更高层图像处理服务. 随着分割技术研究的不断深入, 研究者发现, 对于语义复杂的图像, 只利用单张图像自身信息的分割方法很难准确分割出令人满意的区域.
为解决这一问题, 文献[2]提出组相似活动轮廓模型(active contours with group similarity, ACGS)[2], 针对多张目标形状相似的图像同时进行分割, 利用相似图像之间的冗余信息来弥补单张图像信息的不足, 有效解决了单张图像中目标形状有缺失或被遮挡情形时的分割问题. 该模型用CV模型[3]中的能量项作为单张图像数据项, 用形状矩阵的秩作为图像组相似性约束项. 由于CV模型只适用于分割变化缓慢的均匀图像, 所以ACGS模型对具有纹理变化的形状相似图像组分割效果较差. 此外, ACGS模型对初始轮廓的位置也很敏感.
针对ACGS模型上述的局限性, 文献[4]提出加权组相似活动轮廓模型, 该模型通过给每张图像赋予一个权系数, 来更好地平衡ACGS模型中单张图像数据项和图像间相似性约束项之间的权重问题, 提高了ACGS模型对含噪声相似图像组的分割效果. 文献[5]提出了用不均匀嵌入式活动轮廓模型中的能量泛函作为ACGS模型中的单张图像数据项, 一定程度上提高了ACGS模型对灰度不均匀的相似图像组的分割效果. 文献[6]提出将图像的动态亮度信息加入ACGS模型以更好地分割局部灰度不均的相似图像组, 但由于仍用CV模型作为单张数据项, 所以该模型对具有纹理变化的相似图像组分割效果不好.
本研究针对ACGS模型不能有效分割具有纹理变化图像组的问题, 提出了基于图像局部直方图信息的组相似活动轮廓模型. 该模型中用基于图像局部直方图信息的能量项作为单张图像数据项, 用形状矩阵的秩作为图像间相似性约束项, 既充分考虑单张图像的纹理信息, 又考虑图像间形状的相似性. 在基于自然统计的显著图(saliency using natural statistics, SUN)[7]上演化CV模型实现轮廓的初始化, 提高了ACGS模型对初始轮廓位置的鲁棒性.
1 相关背景
1.1 ACGS模型
给定一组形状相似图像I1, …,In, 待获取图像的目标轮廓为C1, …,Cn. 基于图像之间目标轮廓的相似性, 文献[2]提出了ACGS模型, 该模型能量泛函如下:
(1)
其中:X=[C1, …,Cn]是图像组的形状矩阵, 该矩阵的秩可度量图像间的目标形状的相似性, 当形状都相同则形状矩阵的秩为1, 若一些目标形状改变则矩阵的秩增加.K是个常数,K值越小图像间的目标轮廓越相似.Fi(Ci)是第i张图像基于CV模型的能量项, 表达式为:
(2)
其中:Ω1、Ω2分别表示轮廓线内外部区域;C1、C2分别为区域Ω1、Ω2内的平均灰度值; Length(Ci)是曲线Ci长度;λ1、λ2、μ是对应项的权重.
式(1)中的约束项rank(X)是矩阵的秩, 是个离散算子, 难以优化, 文献[2]提出用下面松弛的形式作为目标函数:
(3)

1.2 LHBWD模型
给定一张灰度图像I:Ω→[0, 255], 对每个像素点x∈Ω, 假定Nx, r为以x为中心,r为半径的局部区域, 定义其局部直方图为:
(4)
相应的累积分布函数表达式为:
(5)
其中: |·|为集合中所含元素的个数.
文献[8]用指数为1的Wasserstein距离衡量两个像素点x1、x2间的局部直方图距离, 即:
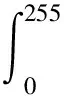
(6)
LHBWD模型[8]用平均局部直方图代替CV模型中的平均灰度, 以更好地分割具有纹理变化的单张图像, 该模型的能量泛函为:
其中:λ1、λ2、μ为对应项的权重;P1、P2分别是轮廓线内部区域Ω1和外部区域Ω2的像素的平均局部直方图;F1、F2分别是相应的累计分布函数, 记:
(8)
该模型用平均局部直方图代替CV模型中的平均灰度, 利用了图像的局部信息, 能够有效地分割具有纹理变化的单张图像. 但当图像前景与背景的灰度、 纹理具有一定相似性时, LHBWD模型可能会有错误的分割.
2 本研究模型
为了有效地分割具有纹理变化的形状相似图像组, 提出了基于局部直方图信息的相似图像组分割模型. 该模型将相似图像组分割问题转化为如下的最优化问题:
(9)

2.1 SUN显著图上获取初始轮廓
ACGS模型对初始轮廓位置敏感, 初始轮廓位置不同, 其最终分割效果往往也不同, 且当初始轮廓设置不恰当时, 甚至会导致图像错误的分割. 针对这一问题, 引入视觉显著性分析机制进行初始轮廓的选取.
首先用SUN显著性检测算法[7]对图像进行显著性分析. SUN是一种基于贝叶斯公式和自然统计算法的图像显著性检测方法. 针对输入的每张图像, 首先提取图像的颜色和亮度特征; 然后基于自然图像统计特征算法、 多尺度的DOG滤波和ICA滤波得到图像特征的概率分布; 最后用图像特征概率的负对数函数(图像特征的自信息代表其显著值)得到图像SUN显著图. 由于图像特征的概率分布是基于自然图像统计特征算法得到的, 使得SUN显著图可以较好地反映图像纹理强度信息. 故选用SUN方法获取图像组的显著图.
通过SUN方法获得的图像显著图, 其显著区域(即目标区域)亮度高, 背景区域较暗, 两个区域亮度对比较大. 有鉴于此, 提出用显著图替换CV模型中图像的灰度图, 即在图像SUN显著图上演化CV模型, 并用演化结果作为初始轮廓. 这样得到的初始轮廓在图像目标的附近, 可以有效地避免背景信息对目标的干扰, 一定程度上也加快了模型收敛速度, 提高了模型的分割效率.
图1为通过显著图检测方法[9-11]及SUN方法[7]得到的猎豹显著图上分别演化CV模型获取初始轮廓的对比图. 第一列为三张猎豹原始图像. 第二列到第五列分别为在猎豹COV显著图[9]、 SEG显著图[10]、 GB显著图[11]和SUN显著图上, 演化CV模型获取的初始轮廓图. 图1中紫色线是得到的初始轮廓线. 由图可知, 通过这种方法获得的初始轮廓在待分割目标的附近, 提高了模型对初始轮廓的鲁棒性. 其次, 将图1第二、 三、 四列分别与第五列对比可知, 在猎豹SUN显著图上获得的初始轮廓更接近目标轮廓, 从而验证了用SUN显著图获取初始轮廓的优势.

图1 CV模型获取初始轮廓的对比图Fig.1 CV model on images saliency maps
2.2 模型求解
利用Nesterov方法[12]求解式(9). 将式(9)写成如下等价形式:

(10)
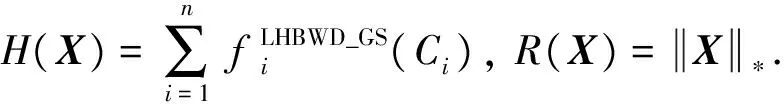
然后, 基于前一个估计值X′, 对H(X)作二次逼近, 即:
(12)
文献[13]中已证明, 当H(X)满足 Lipschitz连续且梯度可微时, 式(12)将以O(1/k)的速度收敛. 接着为了求解问题(12), 引入文献[14]中的定理2.1. 定理内容如下:
给定矩阵X∈Rm×n, 对于如下的优化问题:
(13)
其最优解为X*=Dη(Z), 其中
(14)
σi是向量Z的奇异值,ui,vi分别是Z左右奇异向量, (·)+=max{·, 0},Dη(Z)称为奇异值阈值算子[14].
利用上述定理, 可以得到本研究模型中形状矩阵X的迭代公式:
(15)
其中:
H(Xk)=[
hi(a)=[λ2|F(a,y)-F2(y)|dy-λ1|F(a,y)-F1(y)|dy a+βκana
(16)
a是轮廓Ci上的点,na,κa分别是在点a的法线向量和曲率.
为了提高方法Nesterov收敛速度[13], 在式(15)迭代过程中, 不直接用Xk来更新Xk+1, 而是用线性外推法, 在Xk-1和Xk间取一个值Yk, 并用Yk更新得到Xk+1.Yk表达式为:
(17)
其中:tk是时间步长. 这一改进将式(12)收敛速度提升到O(1/k2), 证明过程请参考文献[13].
下面给出本研究算法框架:
Step1 通过SUN显著图检测方法得到图像组中每张图像的SUN显著图.
Step2 SUN显著图上演化CV模型得到每张图像初始轮廓, 进而得到图像组的初始形状矩阵X0.
Step3 初始化:k=0,X0=X-1, 时间步长t0=t-1=1.
Step4 迭代开始, 利用式(17)得到形状矩阵Yk.
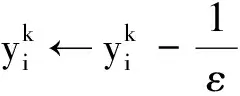
3 实验结果
为了验证本研究模型的有效性, 实验选取了一些经典的图像数据库中的图像组, 包括Caltech库中的2类(即蝴蝶和猎豹图像组)和ETHZ形状数据库[15]中的酒瓶图像组, 实验从每一类中选取6幅图像用于验证. 并通过CV模型、 LHBWD模型、 ACGS模型、 在SUN显著图上获取初始轮廓的ACGS模型及本研究模型的实验结果对比图, 得出本研究模型对于具有纹理变化的相似图像组分割效果优于ACGS模型. 实验硬件环境: CPU 3.20 GHz、 内存 2 GB; 软件环境: Windows XP、 Matlab2012a. 本研究模型对蝴蝶、 猎豹、 酒瓶图像组分割实验中参数设置为: 权重λ1、λ2均取1, 时间步长t均取1, 相似性权重γ分别为20、 5、 15, 迭代终止条件中误差值tolerance分别为4、 1、 1, 求图像的局部直方图时窗口大小均取5. 分割结果详见图1~图4.

图2 五种模型对蝴蝶图像组分割结果Fig.2 The segmentation results of five models for group on butterfly images

图3 五种模型对猎豹图像组分割结果对比图Fig.3 The segmentation results of five models for group on cheetah images


图4 五种模型对酒瓶图像组分割结果对比图Fig.4 The segmentation results of five models for group on bottle images
由图2~4中第二行和第三行可知, 对有纹理变化的图像, CV模型分割效果不好, 易产生过度分割现象; 而LHBWD模型通过将图像中像素点的局部直方图分布相近的归为同一区域, 可以有效避免过度分割现象的产生. 第四行和第五行均为ACGS模型对图像组分割结果, 不同之处为第四行模型的初始轮廓设置为以图像中心为圆心的圆, 而第五行是通过在SUN显著图上实现初始轮廓自适应选取, 这样初始轮廓可从靠近目标物体的周围进行演化, 在一定程度上可避免背景信息对目标的干扰, 提高分割效果, 如图2第4~5行的第2列和图3第4~5行的第3、 4、 6列. 第六行为本研究模型分割效果, 模型中基于图像局部直方图信息的能量项作为单张数据项, 形状矩阵的秩作为图像间相似性约束项. 充分考虑了图像的纹理和形状信息, 同时在图像SUN显著图上演化CV模型得到图像的初始轮廓, 提高了ACGS模型对初始轮廓位置的鲁棒性. 实验结果表明, 对于具有纹理变化的相似图像组, 本研究模型分割效果优于ACGS模型, 如图2第5~6行的第1、 3、 4列, 图3的第5~6行的第4列, 图4的第5~6行的第6列所示.
表1给出五种模型在三组实验中迭代次数和CPU时间的比较. 观察表1可知, 三组实验中, 在SUN显著图上获取初始轮廓的ACGS模型迭代次数和时间都不大于ACGS模型, 说明在SUN显著图上进行初始轮廓的提取是有必要的. 其次, 在参数设置都一致的情况下, 本研究模型达到收敛所需的次数均少于其余四种模型, 比如对蝴蝶、 猎豹、 酒瓶图像组, ACGS模型分别在第32次、 第100次、 第50次收敛, 而本研究模型分别在第7次、 第33次、 第17次已经收敛. 但是, 由于本研究模型在每次迭代过程中, 都需用到图像的局部直方图, 使得该模型运行时间比ACGS模型长些. 然而实验结果表明这种代价是值得的, 因为五组实验中, 本研究模型收敛次数均少于ACGS模型, 且分割结果也都优于ACGS模型.
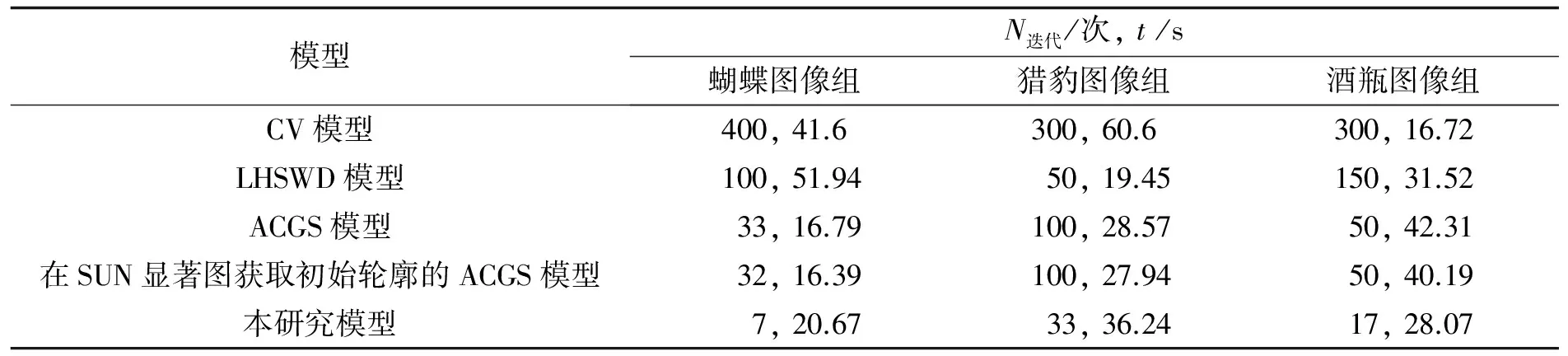
表1 五种模型分别在三组实验中的迭代次数和CPU时间的比较
4 结论
本研究基于LHBWD和ACGS模型, 提出基于局部直方图信息的相似图像组分割模型, 并通过在SUN显著图上演化CV模型获得初始轮廓. 实验结果表明, 与ACGS模型相比, 该模型能够较好地分割具有纹理变化的形状相似图像组, 且对初始轮廓的鲁棒性较强. 但是, 由于图像局部直方图信息的参与使得本研究模型计算量较大, 因此下一步工作将采用不同的优化方案来加快收敛速度.
参考文献:
[1] 王大凯, 侯榆青, 彭进业. 图像处理的偏微分方程方法[M]. 北京: 科学出版社, 2008.
[2] ZHOU X W, HUANG X J, DUNCAN J S,etal. Active contours with group similarity[C]//IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE, 2013: 2969-2976.
[3] CHAN T F, VESE L A. Active contour without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266-277.
[4] LYU P, ZHAO Q, GU D. Segmenting similar shapes via weighted group similarity active contours[C]// IEEE International Conference on Image Processing. Quebec: IEEE, 2015: 4032-4036.
[5] 王婵灿, 舒志彪. 不均匀性嵌入式活动轮廓模型分割相似图像组[J]. 微型机与应用, 2015(20): 39-41.
[6] 陈学灵, 王美清. 结合动态亮度的活动轮廓模型分割相似图像组[J]. 电子设计工程, 2016, 24(7): 164-167.
[7] ZHANG L, TONG M H, MARKS T K,etal. SUN: a bayesian framework for saliency using natural statistics[J]. Journal of Vision, 2008, 8(7): 1-20.
[8] NI K, BRESSON X, CHAN T,etal. Local histogram based segmentation using the wasserstein distance[J]. International Journal of Computer Vision, 2009, 84(1): 97-111.
[9] ERDEM E, ERDEM A. Visual saliency estimation by nonlinearly integrating features using region covariances[J]. Journal of Vision, 2013, 13(4): 11.
[10] RAHTU E, KANNALA J, SALO M,etal. Segmenting salient objects from images and videos[C]// European Conference on Computer Vision. Berlin: Springer-Verlag, 2010: 366-379.
[11] SCHÖLKOPF B, PLATT J, HOFMANN T. Graph-based visual saliency[J]. Advances in Neural Information Processing Systems, 2007, 19: 545-552.
[12] BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. Siam Journal on Imaging Sciences, 2009, 2(1): 183-202.
[13] NESTEROV Y. Gradient methods for minimizing composite objective function[J]. Core Discussion Papers, 2007, 140(1): 125-161.
[15] BRANSON S, WAH C, SCHROFF F,etal. Visual recognition with humans in the loop[C]// European Conference on Computer Vision. Berlin: Springer-Verlag, 2010: 438-451.
