基于行动轨迹的人工蜂群算法

何 尧， 郭文忠， 刘耿耿， 张顺淼

(1. 福建工程学院信息科学与工程学院， 福建 福州 350118； 2. 福州大学数学与计算机科学学院， 福建 福州 350116)

0 引言

人工蜂群(artificial bee colony, ABC)算法由土耳其学者Karaboga[1]于2005年提出， 是受蜂群采蜜行为启发而来的群智能算法， 用于解决单模或多模的优化问题. 由于它操作简单， 控制参数少， 鲁棒性和探索能力强， 受到了很多学者的关注. ABC目前已成熟应用到了数据挖掘[2-4]、 神经网络[5-6]、 图像处理[7-9]等多个领域.

众所周知， 一个好的优化算法需要平衡全局探索能力和局部搜索能力， 而ABC有着较强的全局探索能力， 但局部搜索能力较弱， 收敛速度较慢. 因此， 有相当一部分研究是用于改善ABC的局部搜索能力. 文献[10]采用邻域搜索机制， 从当前蜜源的环形邻域拓扑结构中选择较优的邻居蜜源进行开采， 以平衡算法的探索与开采能力. 文献[11]在标准ABC的基础上添加方向信息， 提出基于方向的人工蜂群算法(directed artificial bee colony, DABC). 它用一个二维数组来保存每个解的每个维度的方向信息， 用来指导该维度参与下次蜜源开采的方向. 文献[12]结合ABC和粒子群优化算法(particle swarm optimization, PSO)的特点， 提出了基于全局最优的ABC算法(gbest-guided artificial bee colony, GABC)， 在方案更新时不仅参考邻域蜜源， 还以全局最优解做指导. 以上研究大大推动人工蜂群的发展， 但在标准ABC及大部分改进算法中， 开采蜜源的策略具有较大的随意性， 随机选择解维度、 方向和开采步伐， 完全忽略以往的搜索经验. 对此本研究提出的基于行动轨迹的蜂群算法(enhanced directed artificial bee colony, EDABC)， 记录下蜜蜂在找寻新蜜源时的行动轨迹， 该信息不仅保存蜜蜂在每个蜜源的每个维度开采成功的方向， 还保留了在该维度开采的连续失败次数， 并以此来确定下次蜜蜂在该维度开采时的方向、 频率和步伐， 从而加快算法的收敛速度， 最后将EDABC在函数优化问题上进行了仿真实验.

1 标准人工蜂群算法

在ABC算法里， 所有的蜜蜂划分为三组： 雇佣蜂、 跟随蜂、 探索蜂. 雇佣蜂和跟随蜂各占蜂群总数的一半. 雇佣蜂负责勘探蜜源并分享信息， 跟随蜂跟随雇佣蜂去采蜜， 当蜜源被开采殆尽后， 探索蜂出动寻找新蜜源. 其中， 每个蜜源的位置代表优化问题的一个可行解， 初始化时随机产生SN个蜜源(均匀分布)， 每个蜜源用xi(i=1, 2, …,SN)表示， D代表优化问题维数. 在对蜂群和蜜源进行初始化后， ABC算法反复执行三个过程： 雇佣蜂阶段、 跟随蜂阶段、 探索蜂阶段来寻找问题的最优解. 每个阶段现描述如下：

1) 雇佣蜂阶段. 在雇佣蜂阶段， 基于以下公式对蜜源进行开采， 寻找新蜜源， 并利用贪婪算法留下更优解.

vij=xij+φij(xij-xkj)

(1)

其中:vij表示vi中第j个纬度(vi是在蜜源xi附近搜索出来的新蜜源);k∈{1, 2, …,SN},j∈{1, 2, …, D}随机生成， 且k≠i;φij是一个取值在[-1, 1]之间的随机值.

2)跟随蜂阶段. 雇佣蜂勘探蜜源后在舞蹈区分享蜜源信息. 跟随蜂基于花蜜量(适应值)以某种策略(标准ABC采用轮盘赌策略， 以实现蜜源的适应值越高， 被观察蜂选中的概率越高)选择某个蜜源进行跟踪开采， 开采过程与雇佣蜂相同.

3)探索蜂阶段(scout bee phase). 如果经过多次迭代后， 某个蜜源不被更新次数超过了预定阈值limit， 那么需抛弃该蜜源， 启动探索蜂阶段. 探索蜂利用公式(2)随机寻找新的解决方案来代替被抛弃的旧方案.

xij=xmin j+rand[0, 1](xmax j-xmin j)

(2)

其中， minj和maxj分别代表第j个维度取值的最小值和最大值.

2 DABC和GABC

DABC[11]是在ABC的基础上添加了方向信息， 让蜜蜂有方向地开采新的蜜源从而加快ABC的收敛速度. 具体见公式(3)：

(3)

式(3)中： abs代表取绝对值函数;dij代表第i解第j维的方向信息， 由它来指导开采新蜜源的方向， 它的取值是由上一次开采时第j维的变化而定;φij是一个取值在[-1, 1]之间的随机值;rij是一个取值为[0, 1]之间的随机值.

受PSO启发， 文献[12]提出了GABC算法， 修改了标准ABC的公式(2)， 加入最优解去引领蜜源开采， 具体见公式(4):

vij=xij+φij(xij-xkj)+ψij(yj-xij)

(4)

其中:yj是最优解的第j维度值；φij为[-1， 1]的随机数；ψij为取值[0，C]的随机数；C是个非负常量.

3 基于行动轨迹的人工蜂群算法

标准ABC算法对蜜源的开采， 具有较大的随意性， 没有积累以往的开采经验. 改进算法DABC只记录了蜜源开采时的每个维度的部分信息——方向， 而对其它有益信息没有记录. 对此可以在不影响DABC算法空间复杂度的情况下， 让DABC算法里的参数dij保存更多蜜蜂开采的轨迹信息，dij的取值由公式(5)所示：

(5)

(6)

在公式(6)中， 新蜜源的产生根据方向的不同采取不同的策略. 其中φij代表[-1， +1]的随机数，rij和ψij都代表[0， 1]的随机数，yj代表全局最优解，dijmod 10用来求dij的个位， 即方向信息. 用dij中记录的连续开采失败次数来调整步长因子s1和s2， 这两个因子分别控制了局部寻优和全局寻优的能力. 设置较大的s1, 会使蜂群发生过多的局部搜索， 而设置较大的s2, 将增强蜂群的开采能力. 当蜂群有明确的方向时(方向信息为1或2)， 较大的s1和较小的s2将使蜂群尽量发散搜索空间， 扩大搜索范围， 增加种群的多样性. 而当蜜蜂没有明确的方向(方向信息为3)， 且连续多次开采失败， 采用较小的s1和较大的s2， 有利于收敛到全局最优解. 具体见公式(7)

(7)

式中:smax为一个常数， 负责平衡s1和s2的取值;cmax为一个固定常量， 当该维度影响值超过cmax时， 则以一定概率用下一维度替换该维度， 以保证减少该维度参与更新的频率. 具体算法描述如下：

1) 初始化阶段.

随机产生SN个蜜源xij,i=1, …,SN;j=1, …， D.

初始化轨迹信息d， 设置每个蜜源的每个维度的初始值为0.

2) 反复执行以下三个阶段， 直到达到最大循环次数(或者其他终止条件).

雇佣蜂阶段：

利用公式(6)开采新蜜源， 并计算适应值.

根据贪婪算法， 如果新蜜源的适应值优于原蜜源， 则保留新蜜源.

根据公式(5)设置新的轨迹信息.

跟随蜂阶段：

跟随蜂根据每个蜜源的适应值采用轮盘赌算法决定是否跟踪开采xi， 开采过程与雇佣蜂开采过程相同.

当发现有被抛弃蜜源时， 执行探索蜂阶段：

探索蜂抛弃该蜜源， 根据公式(2)随机找出全新蜜源代替原来被抛弃的蜜源， 并计算新蜜源的适应值.

重新设置该蜜源的所有维度的方向信息为0，dij=0,i∈[1, …,SN],j∈[1, …, D].

历史最优蜜源与当前解空间里每个蜜源比较， 保留最优蜜源.

3) 输出最优蜜源.

4 算法实例测试

4.1 测试函数及算法参数设置

为了检验EDABC的性能， 本研究选用5个具有代表性的测试函数， 并与ABC、 DABC、 GABC进行比较. 表1列出了5个测试函数的表达式， 最优解和取值范围.

表1 标准测试函数

其中, Sphere是比较简单的单峰可分函数， 容易找到最优值. Rosebrock是单峰不可分的非凸函数， 它的极值点处在一个狭长的抛物线形的山谷里， 且取值范围内走势平坦， 难以通过梯度下降法来收敛到最优点. 其它的函数都是多峰函数， 可以用来测试算法的全局搜索能力， 其中Ackley是多峰不可分函数， 由于其指数项原因， 导致该函数有多个局部最优点. Griewank是多峰不可分函数， 它会随着维数(D>30)的增加而失去多峰特性， 呈现出单峰特性. Rastrigin是多峰可分函数， 它在Sphere函数的基础上添加了余弦调制， 导致其有多个局部最小值. 这五个函数分别代表了寻优问题的不同形式和难度， 被广泛地用来检测算法的性能. 表2列出了算法参数设置.

表2 参数设置

其中GABC的C参照文献[12]为1.5， EDABC 中smax=2.0,cmax=20为经验值. limit的取值由公式(8)计算[13]而得：

limit=SN×D

(8)

4.2 结果与分析

图1 F1函数动态寻优过程(30维)Fig.1 The convergence graph of the methods on the Sphere function(30-D)

依据前述的参数设置， 分别对EDABC与标准ABC、 DABC、 GABC各运行了30遍， 见图1～5所示， 各算法在各函数的迭代寻优过程.实验结果如表3所示.

从图1和表3可看出， 由于Sphere函数比较简单， 所有算法对其寻优结果精度都比较高， 并能稳步收敛. 三个改进算法无论从精度和稳定性来看， 都明显优于原ABC算法， 其中， EDABC精度最高， 并且收敛速度最快. 而对于更难的Rosebrock函数， 所有算法精度明显没有Sphere函数的高， 从图2可发现， 以最优解引领的GABC算法过早收敛. 虽然EDABC在该函数的上精度要比其他算法更高， 但同时它的标准偏差较大， 即稳定性较差. 剩下三个用来测试全局搜索能力的多峰函数， EDABC无论从精度和稳定性来说， 都表现出众， 其中， 通过图5 Rastrigin函数的寻优过程可看出， EDABC表现尤为突出， 具有更强的全局搜索能力， 能快速地跳出局部最优解.

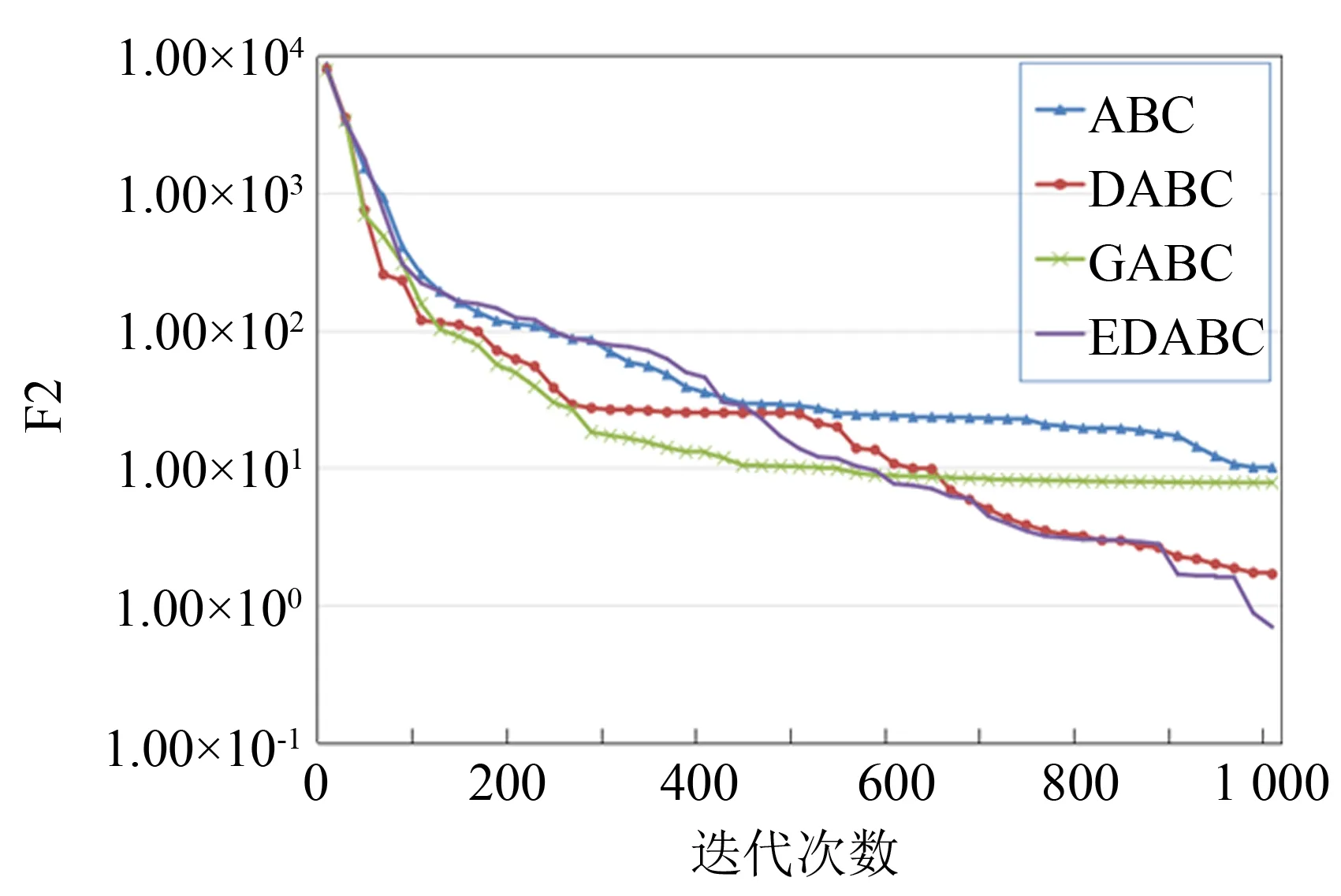
图2 F2函数动态寻优过程(30维)Fig.2 The convergence graph of the methods on the Rosenbrock function(30-D)

图3 F3函数动态寻优过程(30维)Fig.3 The convergence graph of the methods on the Ackley function(30-D)

图4 F4函数动态寻优过程(30维)Fig.4 The convergence graph of the methods on the Griewank function(30-D)

图5 F5函数动态寻优过程(30维)Fig.5 The convergence graph of the methods on the Rastrigin function(30-D)

函数名称评价指标ABCDABCGABCEDABCF1-Sphere最优值7．46×10-126．32×10-164．72×10-163．71×10-18最差值6．50×10-101．17×10-159．70×10-167．53×10-16平均值8．74×10-118．39×10-167．58×10-165．54×10-16标准偏差1．24×10-108．26×10-167．45×10-168．64×10-17F2-Rosenbrock最优值10．04741．68537．79010．6945最差值27．623026．145727．546419．7531平均值20．153810．498221．52487．4061标准偏差4．284310．32364．38537．2902F3-Ackley最优值5．54×10-61．37×10-86．81×10-91．93×10-10最差值6．35×10-53．45×10-74．36×10-88．69×10-10平均值2．47×10-59．55×10-82．40×10-84．61×10-10标准偏差1．23×10-59．45×10-82．36×10-81．66×10-10F4-Griewank最优值2．50×10-145．55×10-164．85×10-162．34×10-17最差值2．168×10-129．99×10-169．99×10-168．88×10-16平均值6．67×10-137．55×10-167．179×10-165．77×10-16标准偏差5．76×10-137．430×10-167．077×10-161．01×10-16

续表3

注：各指标最优值用黑体表示

5 结语

在ABC算法中， 跟随蜂在蜜源附近随意开采， 没有利用以往搜索经验， 为此， 本研究结合DABC和GABC算法特征, 记录蜜蜂开采行为的行动轨迹， 并以此为经验指引蜜蜂下一次开采， 以提高ABC搜索能力. 通过对5个标准函数的寻优测试并与ABC、 DABC、 GABC比较， 实验结果表明， 该算法能有效提高ABC的性能， 并具有良好的稳定性和鲁棒性.

EDABC算法能记录不同维度对寻优的贡献度并采取不同的更新频率和幅度的特性， 更适合解决不确定模型的寻优问题， 下一步工作将考虑把EDABC应用到复杂的组合优化问题和具体应用中， 提出性能更好的全局优化算法.

参考文献：

[1] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Kayser： Erciyes University, Engineering Faculty, Computer Engineering Department, 2005.

[2] OZTURK C, HANCER E, KARABOGA D. Dynamic clustering with improved binary artificial bee colony algorithm[J]. Applied Soft Computing, 2015, 28: 69-80.

[3] CELIK M, KOYLU F, KARABOGA D. CoABCMiner: an algorithm for cooperative rule classification system based on artificial bee colony[J]. International Journal on Artificial Intelligence Tools, 2016, 25(1): 1550028(1-50).

[4] 朱冰莲, 朱方方, 段青言, 等. 采用多策略离散人工蜂群的改进频谱分配算法[J]. 西安交通大学学报, 2016, 50(2): 20-25.

[5] KARABOGA D, KAYA E. An adaptive and hybrid artificial bee colony algorithm (aABC) for ANFIS training[J]. Applied Soft Computing, 2016, 49: 423-436.

[6] MENON N, RAMAKRISHNAN R. Brain tumor segmentation in MRI images using unsupervised artificial bee colony algorithm and FCM clustering[C]// IEEE International Conference on Communications and Signal Processing. [S.l.]: IEEE, 2015: 6-9.

[7] BHANDARI A K, KUMAR A, SINGH G K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions[J]. Expert Systems with Applications, 2015, 42(3): 1573-1601.

[8] ALI M, AHN C W, PANT M,etal. An image watermarking scheme in wavelet domain with optimized compensation of singular value decomposition via artificial bee colony[J]. Information Sciences, 2015, 301: 44-60.

[9] DERICHE R, FIZAZI H. The artificial bee colony algorithm for unsupervised classification of meteorological satellite images[J]. International Journal of Computer Applications, 2015, 112(12): 44-60.

[10] 周新宇, 吴志健, 邓长寿, 等. 一种邻域搜索的人工蜂群算法[J]. 中南大学学报(自然科学版)， 2015, 46(2): 534-546.

[11] KIRAN M S, FINDIK O. A directed artificial bee colony algorithm[J]. Applied Soft Computing, 2015, 26(C): 454-462.

[12] ZHU G P. Gbest- guided artificial bee colony algorithm for numerical function optimization[J] . Applied mathematics and Computation, 2010, 217(7): 3166 -3173.

[13] KARABOGA D, AKAY B. A comparative study of artificial bee colony algorithm[J]. Applied mathematics and Computation, 2009, 214(1): 108-132.